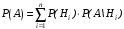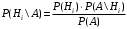Полная вероятность. Формула полной вероятности Практич. занятие-1. Формула полной вероятности Формула Байеса
 Скачать 24.13 Kb. Скачать 24.13 Kb.
|
где события Н1,Н2, ..., Нn, - гипотезы; Р(Hi) – вероятность гипотезы Р(А/Hi) - условная вероятность наступления события А при наступленииi-ой гипотезы (i=1, 2,..., n). Р(Hi/А) - условная вероятность гипотезы Нi; при условии того, что событие А произошло. Формула Байеса позволяет пересмотреть вероятности гипотез после наступления события А. Пример 1. Прибор может работать в трех режимах: нормальном, форсированном и недогруженном. Нормальный режим наблюдается в 60% случаев работы прибора, форсированный – в 30% и недогруженный - в 10%. Надежность прибора для нормального режима равна 0,8, для форсированного - 0,5, для недогруженного - 0,9. Найти полную надежность прибора. Решение. А – безотказная работа прибора (надежность). Событие A может произойти одновременно с одним из следующих событий (гипотез):
По формуле полной вероятности Р(А) = 0,6·0.8 + 0,3·0.5 + 0,1·0,9 = 0,72. Пример 2. В пирамиде 10 винтовок, из которых 4 – с оптическим прицелом. Вероятность поразить мишень из винтовки с оптическим прицелом равна 0,95, без оптического прицела – 0,8. Стрелок поразил мишень из наудачу взятой винтовки. Что вероятнее, стрелок попал из винтовки с оптическим прицелом или без него? Решение. Гипотезы: Н1 – взята винтовка с оптическим прицелом. Н2 – без оптического прицела. Событие А – стрелок попал в мишень. Вероятности гипотез до опыта: Р(Н1)=0,4, Р(Н2)=0,6. Условные вероятности события А: Р(А/Н1)=0,95, Р(А/Н2)=0,8. По формуле полной вероятности Р(А)= 0,4·0,95+0,6·0,8=0,86. Вероятности гипотез после опыта найдем по формуле Байеса: 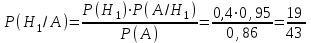 ; ;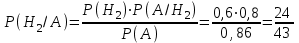 . .Если стрелок поразил мишень, то вероятнее, что он стрелял из винтовки без оптического прицела, т.к. таких винтовок было больше. Задачи для самостоятельного решения 1. При исследовании жирности молока коров все стадо было разбито на три группы. В первой группе оказалось 70%, во второй - 23% и в третьей - 7% всех коров. Вероятность того, что молоко, полученное от отдельной коровы, имеет не менее 4% жирности, для каждой группы коров соответственно равна 0,6, 0,35 и 0,1. Определить вероятность того, что для взятой наудачу коровы жирность молока составит не менее 4%. Взятая наудачу корова дает молоко жирностью не менее 4%. Найти вероятность того, что эта корова из первой группы. 2. В первой урне 10 деталей, из них 8 стандартных. Во второй 6 деталей, из которых 5 стандартных. Из второй урны переложили в первую одну деталь. Какова вероятность того, что деталь, извлеченная после этого из второй урны, нестандартная? 3. Имеются две урны. В первой – 7 красных шаров и 3 черных, во второй – 3 красных и 4 черных. Из первой урны переложили во вторую один шар, затем, перемешав шары, из второй урны переложили в первую один шар. Найти вероятность того, что шар, извлеченный после этого из первой урны, окажется красным. 4. Перед посевом 90% всех семян было обработано ядохимикатами. Вероятность поражения вредителями растений из обработанных семян равна 0,08, растений из необработанных семян – 0,4. Взятое наудачу растение оказалось пораженным. Какова вероятность того, что оно выращено из обработанного семени? 5. В районе 24 человека обучаются на заочном факультете института, из них шесть – на мехфаке, 12 – на агрофаке и 6 – на экономфаке. Вероятность успешно сдать все экзамены на предстоящей сессии для студентов мехфака равно 0,6, агрофака – 0,76 и экономфака – 0,8. Найти вероятность того, что наудачу взятый студент, сдавший успешно все экзамены, окажется студентом экономфака. 6. В первом ящике из 20 деталей 4 бракованных, во втором - из 30 деталей 5 бракованных. Из первого во второй переложили две детали. Найти вероятность того, что деталь, извлеченная после этого из второго ящика, бракованная. 7. Стрелковое отделение получило 10 винтовок, из которых 8 пристрелянных, две нет. Вероятность попадания в цель из пристрелянной винтовки равна 0,6, а из непристреленной - 0,4. Какова вероятность, что стрелок из наудачу взятой винтовки попадет в цель при одном выстреле? Стрелок поразил цель. Какова вероятность того, что он стрелял из пристрелянной винтовки? 8. Для посева изготовлены семена 4 сортов пшеницы. Причем, 20% всех семян 1-го сорта, 30% - 2-го сорта, 10% - 3-го сорта и 40 % - 4-го сорта. Вероятность того, что из зерна вырастет колос, содержащий не менее 40 зерен, для 1-го сорта – 0,5,для 2-го – 0,3, для3-го – 0,2, для 4-го – 0,1. Найти вероятность того, что наудачу взятое зерно даст колос, содержащий не менее 40 зерен. 9. Из 25 студентов группы 5 студентов знают все 30 вопросов программы, 10 студентов выучили по 25 вопросов, 7 студентов по 20 вопросов, трое по 10 вопросов. Случайно вызванный студент ответил на два вопроса. Какова вероятность того, что он из тех трех студентов, которые подготовили 10 вопросов. 10. Запасная деталь может находиться в одной из трех партий с вероятностями 0,2; 0,5; 0,3. Вероятности того, что деталь проработает положенное время без ремонта, равны соответственно 0,9; 0,8 и 0,7. Определить вероятность того, что: а) взятая наудачу деталь проработает положенное время; б) деталь, проработавшая положенное время, взята из второй или третьей партии. |