Документ Microsoft Word. Функцией называют зависимость y от x. x называют переменной или

• Название: Функцией называют зависимость y от x. x называют переменной или
• Дата: 17.05.2023
• Размер: 180.4 Kb.
• Имя файла: Документ Microsoft Word.docx
• Тип: Документы; #1137523

Функцией называют зависимость «y» от «x».

• 
  «x» называют переменной или аргументом функции.
  
• 
  «y» называют зависимой переменной или значением функции.
  
• 
  Запись функции в виде «y(x) = 60x» называют формульным способом задания функции.
  
• 
  Конечно, нужно понимать, что функция «y(x) = 60x» — это не единственная в мире функция. В математике бесконечное множество самых разнообразных функций.
  

СПОСОБЫ ЗАДАНИЯ ФУНКЦИИ

ЗАДАНИЕ ФУНКЦИИ ФОРМУЛОЙ

Через формульный способ задания функции всегда можно сразу по конкретному значению аргумента «x» найти значение функции «y».

Например, рассмотрим функцию, заданную формульным способом.

y(x) = 32x + 5

Найдем значение функции «y» при x = 0. Для этого подставим в формулу вместо «x»
число «0».

Запишем расчет следующим образом.

y(0) = 32 · 0 + 5 = 5

Таким же образом найдем значения «y» при x = 1 и при x = 2.

Найдем значение «y» при x = 1.

y(1) = 32 · 1 + 5 = 37

Теперь найдем значение «y» при x = 2.

y(2) = 32 · 2 + 5 = 64 + 5 = 69
ТАБЛИЧНЫЙ СПОСОБ ЗАДАНИЯ ФУНКЦИИ

С табличным способом задания функции мы уже встречались, когда расписывали таблицу для функции, которая описывает движение автомобиля «y(x) = 60x».

Любую функцию можно записать с помощью таблицы. Для этого достаточно найти несколько значений «y» для произвольно выбранных значений «x».

Рассмотрим функцию

y(x) = −x + 4

Найдем значения «y» при x = −1, x = 0 и x = 1.

Важно!

Будьте внимательны, когда подставляете значение «x» в функцию,
у которой перед «x» есть минус.

Нельзя терять знак минуса, который стоит перед «x».

При подстановки отрицательного числа в функцию вместо «x» обязательно заключайте отрицательное число в скобки. Не забывайте использовать правило знаков.

Подставим в функцию «y(x) = −x + 4» вместо «x» отрицательное число «−1».

Теперь для функции «y(x) = −x + 4» найдем значения «y» при x = 0 и x = 1.

y(0) = −0 + 4 = 4
y(1) = −1 + 4 = 3

Запишем полученные результаты в таблицу. Таким образом мы получили табличный способ задания функции «y(x) = −x + 4».

x	y
−1	5
0	4
1	3

ГРАФИЧЕСКИЙ СПОСОБ ЗАДАНИЯ ФУНКЦИИ

Теперь давайте разберемся, что называют графиком функции и как его построить.

Прежде чем перейти к изучению графического способа задания функции обязательно вспомните, что называют прямоугольной системой координат.

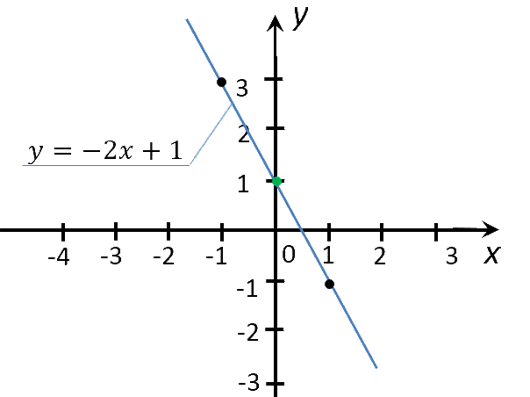
Рассмотрим функцию «y(x) = −2x + 1».

Найдем несколько значений «y» для произвольных «x». Например, для x = −1,
x = 0 и x = 1.

Результаты запишем в таблицу.

x	Расчет
−1	y(−1) = −2 · (−1) + 1 = 2 + 1 = 3
0	y(0) = −2 · 0 + 1 = 0 + 1 = 1
1	y(1) = −2 · 1 + 1 = −2 + 1 = −1

Каждая пара значений «x» и «y» — это координаты точек по оси «Ox» (абсцисса точки) и «Oy» (ордината точки) соответственно.

Назовем каждую полученную точку и запишем их координаты в новую таблицу.

Имя точки	x	y
(·) A	−1	3
(·) B	0	1
(·) C	1	−1

Отметим точки А(−1;3), B(0;1) и С(1;−1) на прямоугольной системе координат.



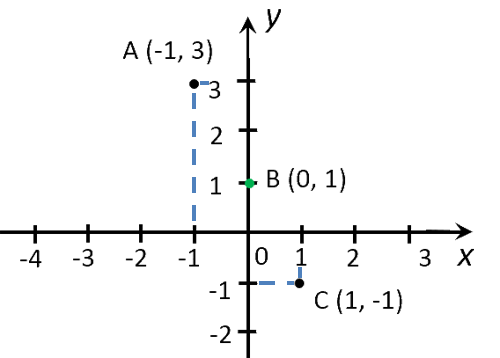
Соединим отмеченные точки прямой. Проведенная прямая будет графиком функции

«y(x) = −2x + 1».



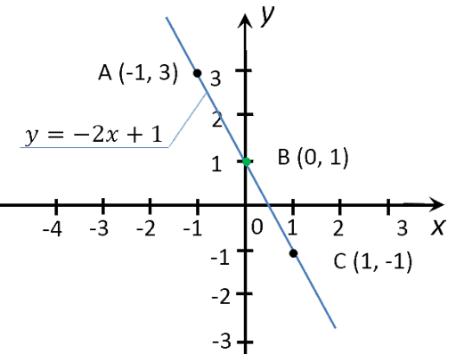
График функции — это объединение всех точек, координаты которых мы можем найти, подставляя в функцию произвольные числовые значения вместо «x».

Другими словами можно сказать, что под графиком функции мы понимаем множество всех точек, координаты которых мы можем найти, подставляя в функцию любые числовые значения вместо «x».

Полученный график функции «y(x) = −2x + 1» это бесконечное множество точек, которые лежат на одной прямой.

При многократном увеличении графика функции мы увидим, что в самом деле вся прямая состоит из рядом стоящих точек.



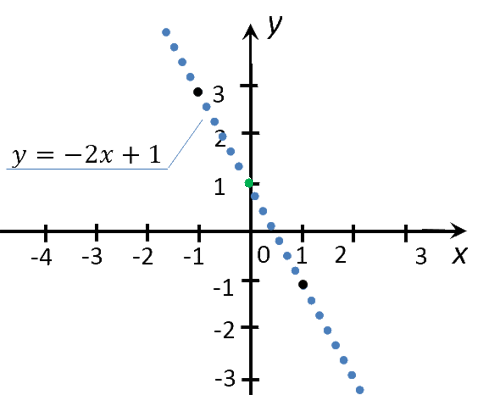
Точки располагаются максимально близко к друг другу, поэтому по расчетам получается, что графиком функции будет являться прямая.