Функции в окружающем мире проект. проект по математике бурмистров никита. Функции в окружающем мире

• Название: Функции в окружающем мире
• Анкор: Функции в окружающем мире проект
• Дата: 11.04.2023
• Размер: 3.88 Mb.
• Имя файла: проект по математике бурмистров никита.docx
• Тип: Документы; #1053524

Муниципaльноe кaзeнноe общeобpaзовaтeльнaя учpeждeниe

,,Сpeдняя общeобpaзовaтeльнaя школa №4’’

имeни Гepоя Совeтского Союзa Знaмeнского В.С. г. Сухиничи

Сухиничского Paйонa Кaлужской облaсти

Тема «Функции в окружающем мире»

Выполнил: учeник 9аклaссa

Буpмистpов Никитa

Pуководитeль: Жapовa О.A


Сухиничи, 2022

Оглавление

Введение 3

История развития понятия функция. 4

Определение функции 12

Линейная функция 14

Обратная пропорциональность 16

Корень n- степени из x 17

Модуль y = | x | 18

Показательная 20

Логарифмическая 21

Функциональные зависимости в повседневной жизни 22

Применения в полётах на невесомость 28

Применение в передачи информации 29

Заключение 34

Приложение 1 35

Введение

В мире всё взаимосвязано. В математике все явления и зависимости описываются с помощью функций. Функция – одно из основных математических и общенаучных понятий, выражающее зависимость между переменными величинами. «Математическими портретами» закономерностей природы и служит функция.

Мы тоже являемся функцией многих переменных, одна из которых – время. Проходят годы, и мы меняемся. Мы также зависим от своей наследственности, от книг, которые мы читаем, от температуры окружающей нас среды и от многих других факторов. И поэтому тему своего исследования я обозначил так: «Функции в окружающем мире». Мы любим находить различные закономерности в окружающем меня мире, любим изучать числа, строить графики. Поэтому мы решили подробнее узнать, как можно связать различные моменты жизни с функциями и графиками.

Цель: Выявить и изучить области применения функции в окружающей жизни.

Актуальность: Работа позволяет развивать интерес школьников к урокам математики, убеждает в высокой практической значимости математической науки, формирует представление о взаимосвязи математики с объектами реального мира, убеждает в необходимости применять полученные знания на практике.


Для достижения поставленной цели нам необходимо решить следующие задачи:

• 
   Проанализировать соответствующую литературу;
  

• 
  Рассмотреть применение функции в точных и естественных науках;
  

• 
  Показать применение функции в природе, науке и жизни человека.
  
• 
  Сделать соответствующие выводы.
  

История развития понятия функция.

Древний период

Большинство математических понятий прошли долгий путь развития. Сложный путь прошло понятие функции. Оно уходит корнями в ту далекую эпоху, когда люди впервые поняли, что окружающие их явления взаимосвязаны. Они еще не умели считать, но уже знали, что чем больше оленей удастся убить на охоте, тем дольше племя будет избавлено от голода; чем сильнее натянута тетива лука, тем дальше полетит стрела. С развитием скотоводства, земледелия, ремесел и обмена увеличивалось количество известных людям зависимостей между величинами.

С древнейшего времени до ⅩⅦ века

Идея функциональной зависимости восходит к древности. Ее содержание обнаруживается уже в первых математически выраженных соотношениях между величинами, в первых правилах действий над числами. В первых формулах для нахождения площади и объема тех или иных фигур. Так, вавилонские ученые (4-5тыс. лет назад) пусть несознательно, установили, что площадь круга прибывает функцией от его радиуса посредством нахождения грубо приближенной формулы: образцами табличного задания функции могут служить астрономические таблицы вавилонян, древних греков и индийцев, а примерами словесного задания функции - теорема о постоянстве отношения площадей круга и квадрата на его диаметре или античные определения конических сечений, причем сами эти кривые выступали в качестве геометрических образов соответствующей зависимости.

ⅩⅦ ВЕК

Начиная лишь с 17 века, в связи с попаданием в математику идеи переменных, представление функции явно и вполне сознательно применяется.

Путь к появлению понятия функции заложили в 17 веке французские ученые Франсуа Виет и Рене Декарт; они разработали единую буквенную математическую символику, которая вскоре получила всеобщее признание. Введено было единое обозначение: неизвестных - последними буквами латинского алфавита - x, y, z, известных - начальными буквами того же алфавита - a, b, c, . и т. Под каждой буквой стало возможным понимать не только конкретные данные, но и многие другие; в математику пришла идея изменения. Тем самым появилась возможность записывать общие формулы. Кроме того, у Декарта и Ферма (1601-1665) в геометрических работах возникает четкое представление переменной величины и прямоугольной системы координат. В своей “Геометрии” в 1637 году Декарт дает понятие функции, как изменение ординаты точки в зависимости от изменения ее абсциссы; он систематически рассматривал лишь те кривые, которые можно точно представить с помощью уравнений, притом преимущественно алгебраических. Постепенно понятие функции стало отождествляться, таким образом, с понятием аналитического выражения - формулы. В 1671 году Ньютон под функцией стал понимать переменную величину, которая изменяется с течением времени (называл в “флюентой”).В “Геометрии” Декарта и работах Ферма, Ньютона и Лейбница представление функции носило по существу интуитивный характер и было связано или с геометрическими, или с механическими представлениями: ординаты точек кривых - функция от абсцисс (x); путь и скорость - функция от времени (t) и т.п.

Определение функции с 17 века до начала 19

Само название “функция” (от латинского functio -совершение, выполнение) впервые было употреблено немецким математиком Лейбницем в 1673г. в письме к Гюйгенсу (под функцией он понимал отрезок, длина которого меняется по какому-нибудь определенному закону), в печати ввел с 1694 года. Начиная с 1698 года, Лейбниц ввел также термины “переменная” и “константа”. В 18 веке появляется свежий взгляд на функцию как на формулу, связывающую одну переменную с другой. Это так называемая аналитическая точка зрения на понятие функции. Подход к такому определению впервые сделал швейцарский математик Иоганн Бернулли (1667-1748), который в 1718 году определил функцию следующим образом: “функцией переменной величины называют количество, образованное каким угодно способ из этой переменной величины и постоянных Для обозначения произвольной функции от x Бернулли применил знак j(x), называя характеристикой функции, а также буквы x или e; Лейбниц употреблял x1, x2 вместо современных f1(x) , f2(x). Эйлер обозначил через f: y, f: (x + y) то, что мы ныне обозначаем через f(x), f(x+y). Эйлер предлагает использовать буквы F, Y и другие. Даламбер сделал шаг вперед на пути к современным обозначениям, отбрасывая двоеточие Эйлера; он пишет, например, jt, j(t+s). Окончательную формулировку определения функции с аналитической точки зрения сделал в 1748 году ученик Бернулли Эйлер (во “Введении в анализ бесконечного” “Функция переменного количества есть аналитическое выражение, составленное каким-либо образом из этого количества и чисел или постоянных количеств”. Так понимали функцию на протяжении почти всего 18 века Даламбер (1717-1783), Лагранж (1736-1813), Фурье (1768-1830) и другие видимые математики. Что касается Эйлера, то он не всегда придерживался выше указанного определения; в его работах понятие функции подвергалось последующему формированию в соответствии с запросами математического анализа. В “Дифференциальном исчислении”, вышедшем в свет в 1755 году, Эйлер дает общее определение функции: “Когда некоторые количества зависят друг от друга таким образом, что при изменении последних и сами они подвергаются изменению, то первые называют функцией вторых”. “Это наименование, - продолжает далее Эйлер - имеет чрезвычайно широкий характер; оно охватывает все способы, какими одно количество определяется с помощью других

Как видно из определенных определений, само понятие функции фактически отождествлялось с аналитическим выражением. Новые шаги в развитии естествознания и математики вызвали и дальнейшее обобщение понятия функции. Одним из нерешенных вопросов, связанных с понятием функции, по поводу которого велась ожесточенная борьба мнений, был следующий: можно ли одну функцию задать несколькими аналитическими выражениями? Большой вклад в разрешение спора Эйлера, Даламбера, Бернулли и других ученых 18 века по поводу того, что стоит понимать под функцией, внес французский математик Жан Батист Жозеф Фурье (1768-1830), занимавшийся в основном математической физикой. В представляемых им в Парижскую АН в 1807-1811 гг. Мемуарах по теории распространения тепла в твердом теле, Фурье привел и первые примеры функций, которые заданы на различных участках различными аналитическими выражениями. Из трудов Фурье следовало, что любая кривая независимо от того, из скольких и каких разнородных частей она состоит, может быть представлена в виде единого аналитического выражения и что имеются также прерывные кривые, изображаемые аналитическим выражением. В своем “Курсе алгебраического анализа” , опубликованном в 1721г. , французский математик О. Коши обосновал выводы Фурье. Таким образом, на известном этапе развития физики и математики стало ясно, что приходится пользоваться и такими функциями, для определения которых очень сложно или даже невозможно ограничиться одним лишь аналитическим аппаратом. Последний стал тормозить требуемое математикой и естествознанием расширение понятия функции.

19 ВЕК

В 1834 году в работе “Об исчезании тригонометрических строк” Н.И.Лобачевский, развивая вышеупомянутое эйлеровское определение функции в 1755г., писал: “Общее понятие требует, чтобы функцией от x называть число, которое дается для каждого x и вместе с x постепенно изменяется. Значение функции может быть дано и аналитическим выражением, или условием, которое подает средство испытывать все числа и выбирать одно из них; или, наконец, зависимость может существовать, или оставаться неизвестной... Обширный взгляд теории допускает существование зависимости только в том смысле, чтобы числа, одни с другими в связи, принимать как бы данными вместе». Ещё до Лобачевского аналогичная точка зрения на понятие функции была высказана чешским математиком Б. Больцано. Таким образом, современное определение функции, свободное от упоминания об аналитическом задании, обычно приписываемое Дирихле, неоднократно предлагалось и до него. В 1837 году немецкий математик П.Л. Дирихле так сформулировал общее определение понятия функции: “y есть функция переменной x (на отрезке a £ x £ b), если каждому значению x на этом отрезке соответствует совершенно определенное значение y, причем безразлично каким образом установлено это соответствие - аналитической формулой, графиком, таблицей либо даже просто словами”.

Примером, соответствующим этому общему определению, может служить так называемая “функция Дирихле” j(x). Эта функция задана двумя формулами и словесно. Она играет известную роль в анализе. Аналитически ее можно определить лишь с помощью довольно сложной формулы, не способствующей успешному изучению ее свойств. Таким образом, примерно в середине 19 века после длительной борьбы мнений понятие функции освободилось от рамок аналитического выражения, от единовластия аналитической формулы. Главный упор в основном общем определении понятия функции делается на идею соответствия. Во второй половине 19 века после создания теории множеств в понятие функции, помимо идеи соответствия была включена и идея множества. Таким образом, в полном своем объеме общее определение понятия функции формулируется следующим образом: если каждому элементу x множества А поставлен в соответствие некоторый определенный элемент y из множества В, то говорят, что на множестве А задана функция y=f(x), или что множество А отображено на множество В. В первом случае элементы x множества А называют значениями аргумента, а элементы их множества В - значениями функции; во втором случае x - прообразы, y - образы. В современном смысле рассматривают функции, определенные для множества значений x, которые возможно, и не заполняют отрезка a £ x £ b, о котором говорится в определении Дирихле. Достаточно указать, например, на функцию-факториал y=n! заданную на множестве натуральных чисел. Общее понятие функции применимо, конечно, не только к величинам и числам, но и к другим математическим объектам. Например, к геометрическим фигурам. При любом геометрическом преобразовании мы имеем дело с функцией. Другими синонимами термина “функция” в различных отделах математики являются: соответствие, отображение, оператор, функционал и др.

Дальнейшее развитие математической науки в 19 веке основывалось на общем определении функции Дирихле, ставшим классическим.

Развитие с 19-го века по настоящее время

Уже с самого начала 20 века определение Дирихле стало вызывать некоторые сомнения среди части математиков. Еще важнее была критика физиков, натолкнувшихся на явления, которые потребовали более широкого взгляда на физику. Необходимость дальнейшего расширения понятия функции стала особенно острой после выхода в свет в 1930 году книги “Основы квантовой механики” Поля Дирака, крупнейшего английского физика, одного из основателей квантовой механики. Дирак ввел так называемую дельта-функцию, которая выходила далеко за рамки классического определения функции. В связи с этим советский математик Н.М. Гюнтер и другие ученые опубликовали в 30-40 годах нашего столетия работы, в которых неизвестными являются не функции точки, а “функции области”, что лучше соответствует физической сущности явлений. Так, например, температуру тела в точке практически определить нельзя, в то время как температура в некоторой области тела имеет конкретный физический смысл. В общем виде понятие обобщенной функции было введено французом Лораном Шварцем. В 1936 году, 28-летний советский математик и механик С.Л. Соболев первым рассмотрел частный случай обобщенной функции, включающей и дельта-функцию, и применил созданную теорию к решению ряда задач математической физики. Важный вклад в развитие теории обобщенной функции внести ученики и последователи Шварца - И.М. Гельфант, Г.Е. Шилов и др.

Вывод

Функция-это понятие, которое развивалось одновременно с человечеством, и всегда была рядом. По началу люди не пытались как-либо систематизировать зависимости, но со времен математики, ученые начали задумываться о зависимости одной переменной от другой, и это стало огромным поводом для споров в научном мире. Первым человеком, который начал развивать тему зависимости был математик Декарт. В дальнейшем понятие функции развивалось, и получало множество новшеств, которые также стали темами для множества дискуссий, и развивается сих пор, но уже в очень медленно.

Определение функции

Определение. Числовой функцией с областью определения D называется соответствие, при котором каждому числу x из множества D сопоставляется по некоторому правилу единственное число y, зависящее от x. Принято называть x независимой переменной или аргументом, а у — зависимой переменной или значением функции.

Записывают указанное соотношение между x и у в общем виде так: у = f (x) или у = F (x) и т. п.

График функции y = f (х) - это множество всех точек плоскости, координаты (х, у) которых удовлетворяют соотношению y = f(x).

Способы задания функции:

1. 
   аналитический (с помощью формулы);
   
2. 
   графический;
   
3. 
   табличный;
   
4. 
   словесный.
   

Функции, изучаемые в школе:

1. 
   линейная y = ax + b;
   
2. 
   квадратичная y = ax² + bx + c;
   
3. 
   обратная пропорциональность ;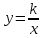
   
4. 
   корень n- степени ;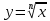
   
5. 
   модуль y = | x |;
   
6. 
   тригонометрические y = sinx, y = cosx, y = tgx, y = ctgx;
   
7. 
   показательная ;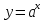
   
8. 
   логарифмическая .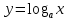
   
   
   

Аналитический способ

Функцию можно задать с помощью аналитического выражения (например, формулой). В этом случае её обозначают как соответствие в форме равенства.

Примеры:

Функция, заданная одной формулой:

f(x)=x+1

Графический способ

Функцию можно также задать с помощью графика. Это множество точек часто является гиперповерхностью. В частности, при {y= n=1}n=1 график функции в некоторых случаях может быть изображён кривой в двумерном пространстве.

Для функций трёх и более аргументов такое графическое представление не применимо. Однако и для таких функций можно придумать наглядное полу геометрическое представление (например, каждому значению четвёртой координаты точки сопоставить некоторый цвет на графике, как бывает на графиках комплекс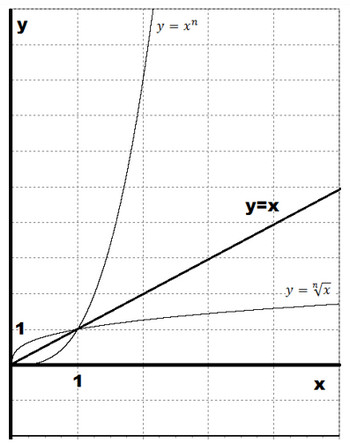

Линейная функция

Л 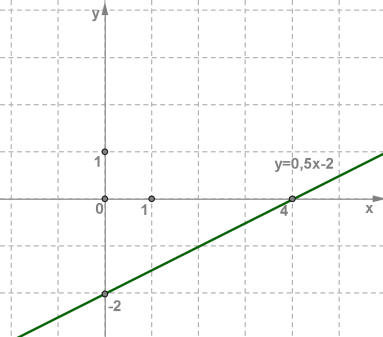инейная функция у=kx+b, графиком является прямая.

Квадратичная функция.

Квадратичной функцией называется функция, которую можно задать y = ax2 + bx + c, где x – переменная, a, b и c – некоторые числа, причем a ≠ 0. Изучение квадратичной функции мы начнем с частного случая, а именно с функции y = ax2. Мы уже встречались с функцией y = x2, когда a = 1. Ее графиком является парабола.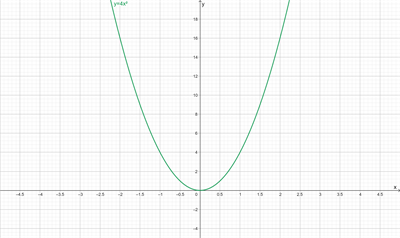



Обратная пропорциональность

При одинаковой продуктивности количество школьников, решающих конкретную задачу, обратно пропорционально времени выполнения этой задачи; количество конфет, купленных на определенную сумму денег, обратно пропорционально их цене; время на маршрут и скорость, с которой путь был пройден — обратно пропорциональные величины.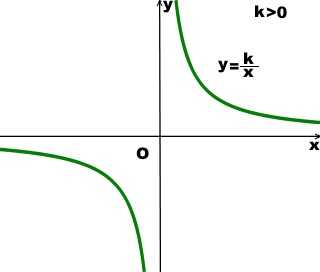




Корень n- степени из x

Корнем n-ой степени из неотрицательного числа aназывают такое неотрицательное число, при возведении которого в степень n получается число а.

Корнем нечётной степени n-ой из отрицательного числа а называют такое отрицательное число, при возведении которого в степень n получается а.



Модуль y = | x |

Проезд машины из точки А в точку Б

Соответственно, при x≥0 график модуля — прямая пропорциональность y=x, при x<0 — y= -x. То есть график функции y=|х| состоит из двух лучей  — биссектрисы I и биссектрисы II координатных углов.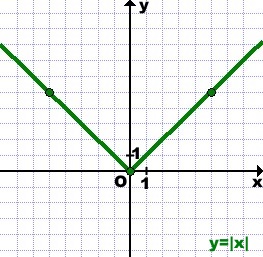

Тригонометрические y = sinx, y = cosx, y = tgx

y=cosx, примером является математический маятник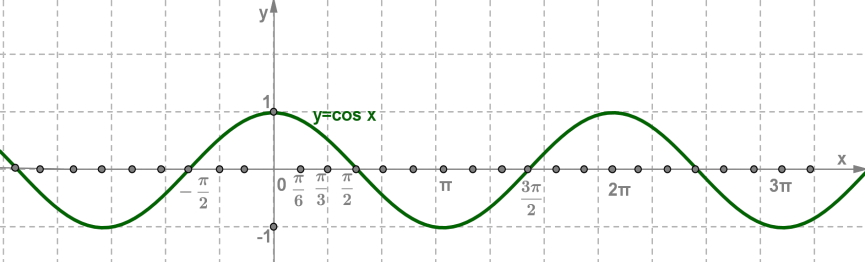



y=sinx, примером является математический маятник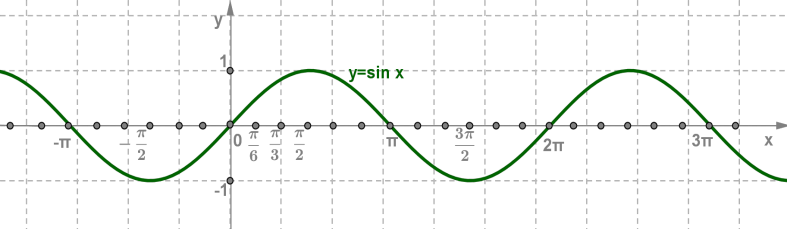



y = tgx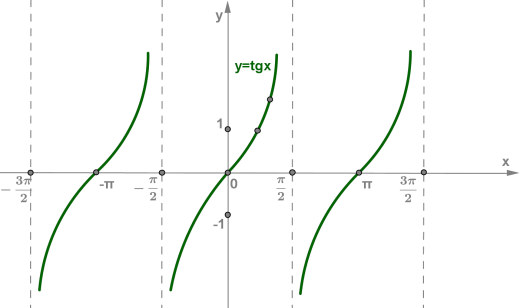




Показательная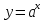

Ф 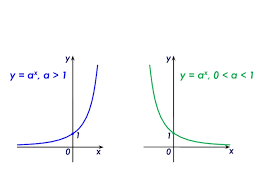ункция вида y = a x , где a — заданное число, x — переменная. Такие функции называют показательными. Это название объясняется тем, что аргументом показательной функции является показатель степени, а основанием степени — заданное число.

Логарифмическая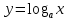

Логарифмической функцией называется функция вида y = log_ax, где a > 0 и a ≠ 1. Рассмотрим свойства функции: Областью определения функции является множество всех положительных чисел D(y) = (0; +∞). Множеством значений функции являются все действительные числа R.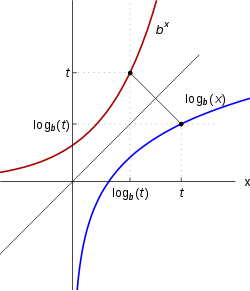

Функциональные зависимости в повседневной жизни

В повседневной жизни мы постоянно сталкиваемся с функциональными зависимостями. Мы нашли множество примеров функций, которые изобразили с помощью графиков.

Пример 1. Рассмотрим деление праздничного торта между гостями. Отчего зависит количество порций? – от числа гостей. А от чего зависит вес порции? – тоже от числа гостей.

− В первом случае, чем больше гостей, тем на большее количество порций мы должны разделить торт .

З 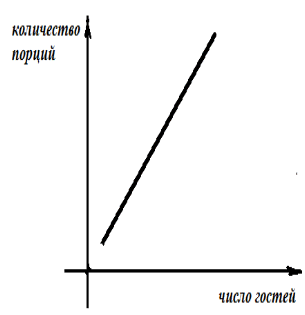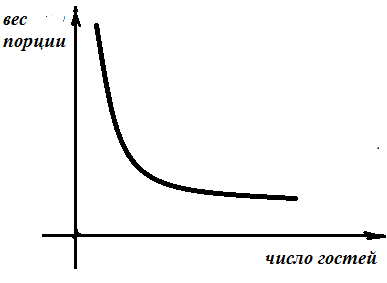десь наглядно можно представить прямую пропорциональную зависимость.

В
Рис. 2
о втором случае, чем больше гостей, тем меньше вес порции. Здесь мы видим обратную пропорциональную зависимость.


П 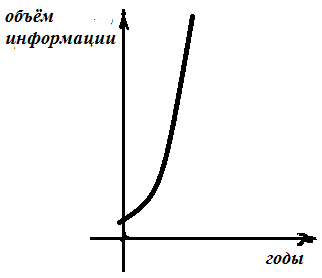ример 2. Мы живём в век информационных технологий. Ежедневно мы получаем массу информации из различных источников: телевидения, радио, газет, журналов, и, конечно, из Интернета. Известно, что объём информации каждые пять лет увеличивается в два раза.

Если построить график зависимости объёма информации от времени, то получим некоторую кривую, которая в математике называется экспонентой и является графиком показательной функции.
Пример 3. Траектория и скорость полёта мяча от силы, приложенной к нему (в нормальных условиях)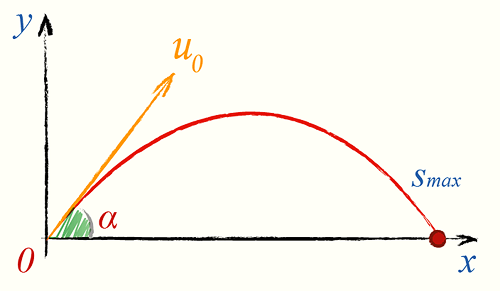



Пример 4. Состояния воды в зависимости от температуры и давления.

Максимально известная зависимость, любому человеку.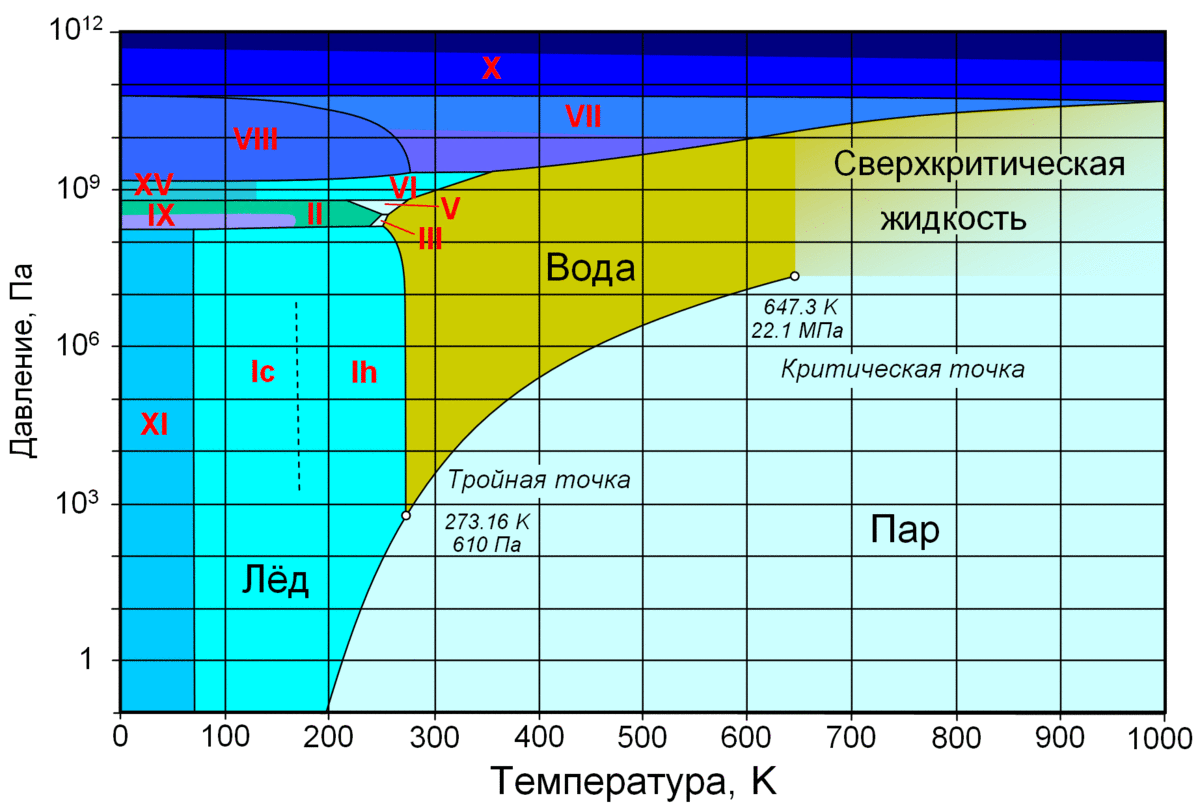




Пример 5. График зависимости от (давления и температуры) агрегатного состояния вещества.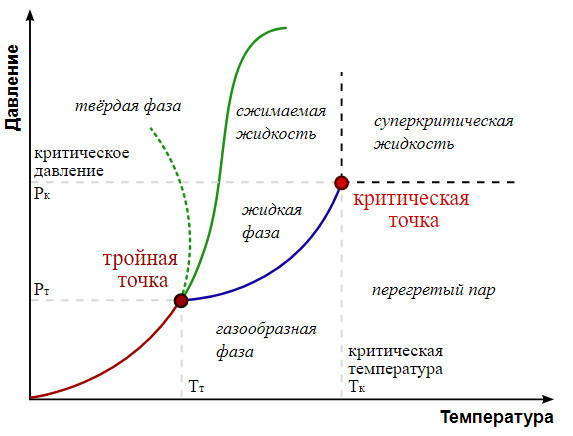


Пример 6. Медицина и графики Кардиограмма Энцефалограмма Лечением людей с сердечно-сосудистыми заболеваниями занимаются врачи-кардиологи. Проводя лечение, врач должен брать на заметку все происходящее, что поможет назначить правильные лекарственные препараты. Чтобы быть достаточно уверенным при назначении лечения врач обращается к помощи электрокардиограммы. Под кардиограммой подразумевается кривая (график), с помощью которой можно определить истинную активность сердечной мышцы. Под кардиограммой и энцефалограммой подразумевается кривая (график), с помощью которой можно определить истинную активность сердечной мышцы в кардиограмме и активность мозговой деятельности в энцефалограмме.

Применения в полётах на невесомость

Такая траектория называется Параболой Кеплера. Сначала самолет летит горизонтально, затем набирает высоту поднимаясь по траектории параболы, при достижении верхней точки параболы силы тяготения и сила инерции уравниваются, и возникает невесомость.

Узнать больше о полетах в невесомость можно узнать в приложении 1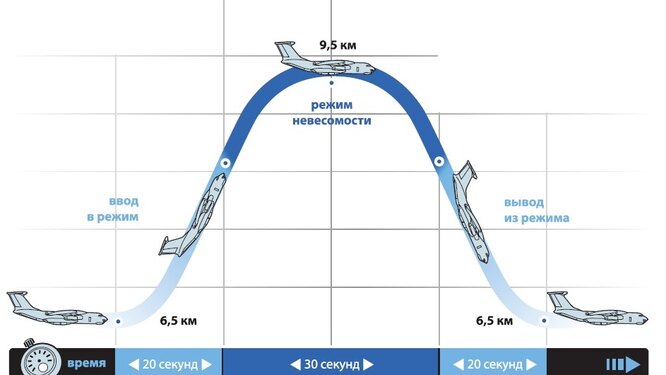



Применение в передачи информации

С 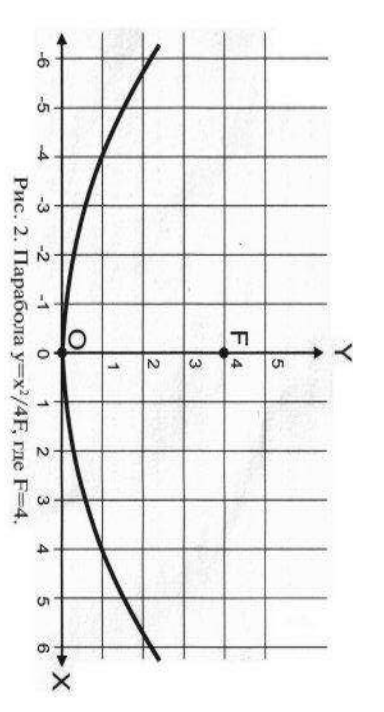войство фокуса параболы используют в телескопических антеннах

Применение в архитектуре

Под действием собственного веса и веса мостового пролёта тросы провисают и образуют дугу, близкую к параболе. Ненагруженный трос, подвешенный между двумя опорами, принимает форму т. н. «цепной линии», которая близка к параболе в почти горизонтальном участке. Если весом тросов можно пренебречь, а вес пролёта равномерно распределён по длине моста, тросы принимают форму параболы.
Эйфелева башня в Париже

Мост Сантьяго Калатравы


Город искусств и наук в Валенсии

Бизнес центр Москва в г. Астана

Параболы в природе

Мыс Бурхан(Байкал)

Уникальная скала Парабола на хребте Ергаки, Западный Саян.



Радуга-парабола

Дельфины выпрыгивают из воды и двигаются по параболе

Заключение

В ходе работы над проектом я проанализировал и изучил литературу и различные Интернет-ресурсы по истории развития функции, применении её в науке и технике. Обзор развития понятия функции приводит к мысли о том, что эволюция ещё далеко не закончена и, вероятно, никогда не закончится, как никогда не закончится и эволюция математики в целом. Новые открытия и запросы естествознания и других наук приведут к новым расширениям понятия функции и других математических понятий.

Изучая и анализируя области применения и взаимосвязь математических функций не только с естественными, но и гуманитарными науками, я решил поставленные задачи и достиг цели проекта.

Я убедился в том, что функция является неотъемлемой частью нашей жизни и наук в целом, так как функциональные зависимости, действительно, существуют во всех сферах жизни человека.

Приложение 1

Первые шаги

Н а заре космической эры никто не знал, как влияет состояние невесомости на человеческий организм и технику. Получить ответы на эти вопросы было необходимо, прежде чем проводить на орбите долговременные эксперименты. Поэтому в 1960 году невесомость начали имитировать во время полетов на учебно-тренировочных МиГ-15. Пилот разгонял самолет и выполнял «горку», а космонавт, находившийся позади него в кабине, учился выполнять в условиях невесомости различные действия — писал в блокноте, пил воду и т. п. Но тесная кабина истребителя не позволяла совершать свободные движения, там нельзя было разместить всю нужную аппаратуру. Вскоре появились специально оборудованные летающие лаборатории Ту-104АК, где во время полетов космонавты учились надевать скафандры, работали на макетах кораблей и орбитальных станций. Именно в этой летающей лаборатории Алексей Леонов учился выходить в открытый космос, там же испытывали работу «лунохода». В 1980-х эстафету приняла специальная модификация транспортного самолета Ил-76К, а в 1990-х — Ил-76МДК (именно на них сейчас проходят подготовку космонавты и астронавты в ЦПК). Таких переоборудованных самолетов всего три, но летает обычно лишь один — остальные два находятся в горячем резерве.

Небесный гигант

Р азмеры российского Ил-76МДК позволяют без проблем разместить внутри достаточно крупные макеты модулей космической станции.

Обслуживание и конструкция «Небесного Кита»

По внешнему виду самолеты, которые обслуживают ЦПК, — Ил-76МДК 70-го ОИТАПОН (отдельного испытательно-тренировочного авиационного полка особого назначения) им. В.С. Серегина, стоящие на подмосковном аэродроме «Чкаловский», — мало отличаются от обычных транспортников. Тем не менее самолеты эти специальные. Возле одного из них работают техники, занимаясь подготовкой самолета к завтрашнему полету, а Николай Третьяков, заместитель командира 1-й эскадрильи авиаполка по инженерно-авиационной службе (ИАС), объясняет мне основные отличия: «в невесомости, как известно, все жидкости ведут себя совершенно по-другому. Это относится и к топливу, и к маслу, и к гидравлическим жидкостям. Поэтому, для того чтобы обеспечить бесперебойную подачу топлива, самолет оборудован топливными и масляными аккумуляторами. Они снабжают двигатели топливом во время режимов невесомости. Кроме того, во время таких полетов перегрузка достигает двух единиц, что, вообще говоря, не слишком типично для транспортного самолета. Поэтому планер самолета также усилен соответствующим образом».

Безопасность самолёта

Полеты по параболической траектории довольно рискованны, поскольку самолет подвергается большим нагрузкам. В случае какой-либо нештатной ситуации он немедленно переходит в горизонтальный полет, и все участники полета покидают борт с парашютами. Хотя кресел с ремнями безопасности в лабораторном отсеке нет, при взлете и посадке можно использовать откидные сиденья и поручни. 1. Рабочие места инженеров-испытателей. 2. Мягкие маты. 3. Сетка. 4. Вращающееся кресло. 5. Лабораторный отсек.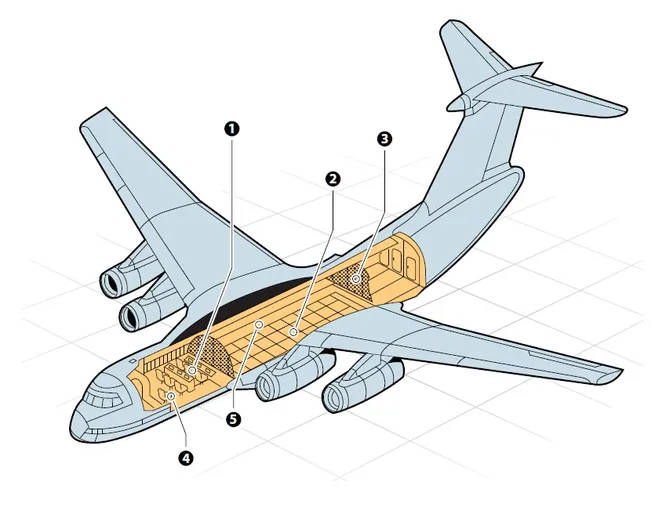



По трапу мы поднимаемся в самолет, и Николай продолжает экскурсию: «салон тоже специально оборудован. В передней части около кабины пилотов кресла для испытательной бригады — руководителя, инженера по освещению и электропитанию, два рабочих места для врачей. Вот здесь иногда устанавливается вращающееся кресло — для испытаний космонавтов на предельных режимах». За креслами — просторный салон без всяких кресел, пол которого застилают толстые мягкие пенополиуретановые маты. Стены и потолок также покрыты мягким материалом. «Это чтобы в невесомости никто себе синяков не набил, — поясняет Николай. — А вот у самого пола — это система подачи воздуха для подключения скафандров. Иногда здесь ставят и макеты модулей космической станции, на которых космонавты тренируются отрабатывать различные ситуации». Я скептически смотрю на узкую дверь, через которую только что попал внутрь. Николай, перехватив мой взгляд, усмехается: «самолет-то транспортный!» — и ведет меня в заднюю часть салона, где старший авиатехник роман Зверев открывает крышку пульта на стене и нажимает несколько клавиш. С громким гулом в задней части самолета откидывается рампа, открывая широченный «въезд».

"Коньяк"

(Удобный индикатор невесомости у второго пилота — мензурка с глицерином, окрашенным в янтарный цвет.)

В кабине пилотов тесно, и глаза разбегаются от обилия различных шкал, стрелок, кнопок, тумблеров и рычагов. «Приборы и органы управления стандартные, есть только небольшие отличия», — говорит Николай. — Вот эти клапаны управляют топливными и масляными аккумуляторами, да еще перед командиром на пульте расположен тумблер, отключающий речевой информатор, чтобы не паниковал: автопилот здесь стандартный, и он не приучен к таким необычным режимам, как параболический полет». Еще одно отличие — два дополнительных индикатора невесомости: перед командиром и вторым пилотом к пульту прикреплены две мензурки с глицерином (в невесомости воздушный пузырь «всплывает» в центр). В одной мензурке глицерин прозрачный, в другой — янтарного цвета. «Коньяк и водка!» — шутит Николай. На прощание механики рассказывают мне байку о том, как пилот одного из коммерческих рейсов заметил Ил-76МДК, выходивший из режима невесомости, и доложил диспетчеру о «падающем самолете».

Процесс полёта по параболе

« Сказочники! — улыбается один из летчиков, заместитель командира полка Игорь Клименко. — для таких полетов выделяется специальная зона и высоты от шести до десяти тысяч метров при условии отсутствия облачности, и никаких коммерческих рейсов там не может быть в принципе. Обычно мы летаем в районе Плещеева озера, по нему удобно визуально ориентироваться». Полет выполняется по так называемой параболе Кеплера и начинается с горизонтального разгона на высоте примерно 6500 м. Затем самолет делает «горку» — на восходящей части происходит ввод в режим невесомости, при этом перегрузка достигает двух единиц. «Управление осуществляется вручную», — объясняет Игорь, — при этом нагрузка на штурвале составляет примерно 70 кгс. Представьте себе штангу такой массы, только поднимать ее нужно не рывком, а плавно и с ювелирной точностью. Причем необходимо очень тщательно следить за креном и боковым смещением — они должны быть нулевые, иначе тех, кто в салоне, ‘размажет' по стенам». Из-за больших физических нагрузок командир и второй пилот, как правило, выполняют режимы невесомости по очереди.

При достижении угла кабрирования примерно в 50 градусов летчик «отдает» штурвал от себя, вводит самолет в 25−30-секундный режим невесомости и осуществляет контроль по индикатору перегрузки и по упомянутому выше «стаканчику». С высоты примерно 9500 м самолет пикирует и переходит (опять-таки с перегрузкой до двух единиц) в горизонтальный полет. Несколько минут такого полета требуется для того, чтобы выполнить разворот, а также зарядить топливные и масляные аккумуляторы. «Формально разрешается выполнять три режима без ‘перезарядки’, а технически ‘запас прочности’ еще в три раза выше», — говорит Игорь Клименко. — но зачем лишний раз рисковать, если в этом нет никакой необходимости? Безопасность для нас всегда приоритетна». Затем все повторяется — за один полет Ил-76МДК выполняет в среднем десять режимов невесомости.

Список используемой литературы

1. 
   Виленкин Н. Я. Функции в природе и технике: Книга для внеклассного чтения 9 – 10 кл. – 2 – е изд., испр. – М.: Просвещение, 1993.
   
2. 
   Е. Канин «Начала в изучении функций», Москва 2005 г., Чистые пруды.
   
3. 
   Сивашинский И.Х. «Элементарные функции и графики» «Просвещение»,1965
   
4. 
   https://studopedia.info/9-25538.html
   
5. 
   https://xn--b1aaibpxdlb1adm.su/second/vse-o.php
   
6. 
   https://www.polnaja-jenciklopedija.ru/
   
7. 
   https://www.yaklass.ru/