функция одной переменной. Функция одной переменной. Функция одной переменной. Основные определения. Способы задания функций. Основные элементарные функции
 Скачать 0.54 Mb. Скачать 0.54 Mb.
|
|
Классификация точек разрыва. Определение. Точка х0 называется точкой разрыва 1- го рода, если в этой точке функция f(x) имеет конечные, но не равные друг другу левый и правый пределы. Определение. Точка х0 называется точкой разрыва 2 – го рода, если в этой точке функция f(x) не имеет хотя бы одного из односторонних пределов или хотя бы один из них бесконечен Непрерывность функции на отрезке. Основные теоремы о функциях, непрерывных на отрезке. Определение. Функция y=f(x)непрерывна на промежутке X, если она непрерывна в каждой точке этого промежутка Теоремы. Теорема 1 (об ограниченности непрерывной функции). Если функция f(x) непрерывна на отрезке [a, b], то она ограничена на этом отрезке, т.е. существует такое число C> 0, что "x О [a, b] выполняется неравенство |f(x)| ≤ C. Теорема Вейерштрасса: Если функция непрерывна на [a,b] то на этом отрезке она достигает своих наибольших и наименьших значений Теорема (вторая теорема Больцано - Коши) Если f непрерывна на I и в двух его точках a и bf(a)=A>B=f(b), то для всякой точки C∈[B,A] между точками a и b найдется хотя бы одна точка c, что f(c)=C. Теорема 3 (о существовании нуля). Если функция f(x) непрерывна на отрезке [a, b] и на концах отрезка принимает ненулевые значения разных знаков, то на интервале (a,b) найдется по крайней мере одна точка ξ в которой f(ξ) = 0. Cуществование непрерывной обратной функции Пусть функция y = f(x) определена, строго монотонна и непрерывна на отрезке [a,b]. Тогда на отрезке [α, β] ( α = f(a), β = f(b) ) cуществует обратная функция x = g(y), также строго монотонная и непрерывная на отрезке (α, β). Свойство 1. Если функция y=f(x) непрерывна на отрезке [a;b], то она ограничена на этом отрезке. Свойство 2. Если функция y=f(x) непрерывна на отрезке [a;b], то она достигает на этом отрезке наименьшего значения m и наибольшего значения M. Свойство 3. Если функция y=f(x) непрерывна на отрезке [a;b] и значения ее на концах отрезка f(a) и f(b) имеют противоположные знаки, то внутри отрезка существует, по крайней мере, одна точка cϵ(a;b), такая что f(с)=0. Задачи, приводящие к понятию производной. а)о скорости движения материальной точки б) об угле наклона касательной к графику функции Определение производной. Связь между непрерывностью и дифференцируемостью функции. Определение: Предел отношения приращения функции к приращению ее аргумента при стремлении приращения аргумента к нулю, если такой предел существует. Функцию, имеющую конечную производную (в некоторой точке), называют дифференцируемой (в данной точке). Определение через предел: Пусть в некоторой окрестности точки x0R определена функция f:U(x0)R→R. Производной функции fв точке x0 называется предел, если он существует, Связь между непрерывностью и дифференцируемостью функции Теорема. Если функцияy=f(x) дифференцируема в произвольной точкеx0, то она непрерывна в этой точке Основные правила дифференцирования Теорема 1. Если функции Формула обобщается на случай любого конечного числа слагаемых. Теорема 2. Если функции Следствие. Постоянный множитель можно выносить за знак производной: Теорема 3. Если в данной точке х функции Производные основных элементарных функций 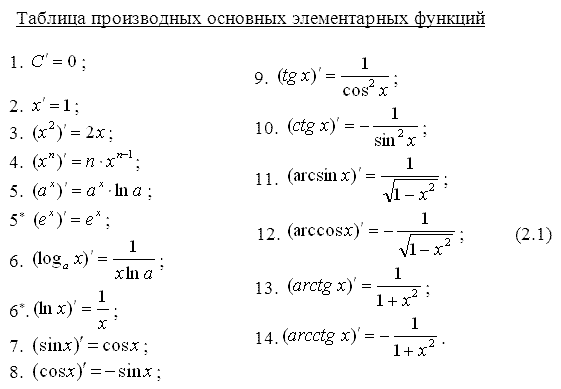 Дифференцирование сложной функции Дифференцирование параметрически заданных функций. 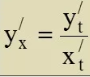 Высшего порядка 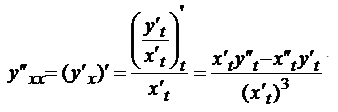 Дифференцирование неявно заданных функций Под неявным заданиемфункции понимают задание функции в виде уравнения F(x;y)=0, не разрешенного относительно у. Всякую явно заданную функцию у=ƒ (х) можно записать как неявно заданную уравнением ƒ(х)-у=0, но не наоборот. Пример: x2+y2-xy=7 y|=? y|(3,1)=? (x2+y2-xy)|=7| 2x+2y*y|-(y+xy|)=0 y|= 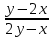 y|(3,1)= y|(3,1)=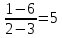 Логарифмическое дифференцирование. Дифференцирование показательно-степенных функций Логарифмическое дифференцирование 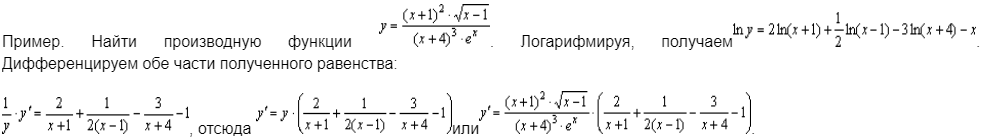 Показательно-степенных функций 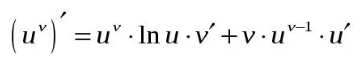 Дифференциал функции. Геометрический смысл дифференциала. Свойства дифференциала. Применение дифференциала к приближенным вычислениям. Дифференциал функции Определение. Дифференциалом функции называют произведение производной этой функции к приращению аргументов dy=y\(x)Δx(1) dy=y\(x)dx(2) Геометрический смысл дифференциала 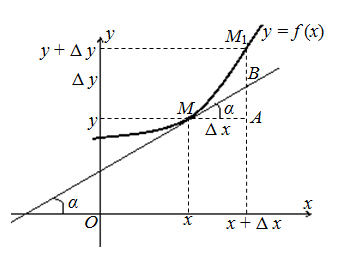 Вывод: дифференциал функции показывает приращение ординаты касательной Свойства дифференциала: 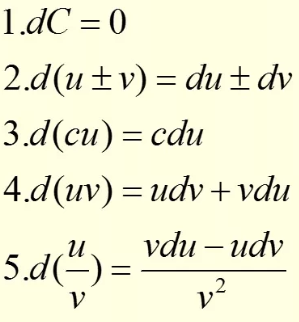 Применение дифференциала к приближенным вычислениям ∆у≈dy y(x+Δx)≈y(x)+y\(x)*Δx Для сложной: где Производные и дифференциалы высших порядков dnx=y(n)(x)*(dx)n Пусть функция f(x) определена и дифференцируема на некотором промежутке X, тогда ее производная Уравнения касательной нормали к кривой. Уравнение касательной к данной кривой в точке Уравнение нормали к данной кривой в точке Основные теоремы дифференциального исчисления. Теорема Ферма. Теорема Ферма (о равенстве нулю производной) Пусть функция y = f(x): 1)дифференцируема на интервале (a;b) , 2)достигает экстремума в точке x0 (a;b) . Тогда производная в этой точке f ′(x0 ) = 0 Основные теоремы дифференциального исчисления. Теорема Ролля. . Теорема Ролля. (о производной функции, принимающей на концах отрезка равные значения).Пусть функция y = f (x) 1)непрерывна на отрезке [a;b]; 2)дифференцируема на интервале (a;b) ; 3)на концах отрезка [a;b] принимает равные значения: f(a) = f(b) . Тогда на интервале(a;b) найдется по крайней мере одна точка x0 , в которой f ′(x0 ) = 0 Теорема Ролля имеет простой геометрический смысл: найдется хотя бы одна точка, в которой касательная к графику функции будет параллельна оси абсцисс. Если f (a)= f (b)= 0, то теорему Ролля можно сформулировать так: между двумя последовательными нулями дифференцируемой функции имеется хотя бы один нуль производной Основные теоремы дифференциального исчисления. Теорема Лагранжа. Теорема Лагранжа (о конечных приращениях). Пусть функция y = f(x) : 1)непрерывна на отрезке [a;b]; 2)дифференцируемана интервале (a;b) . Тогда на интервале (a;b) найдется по крайней мере одна точка x0 такая, что Основные теоремы дифференциального исчисления. Теорема Коши. Теорема Коши (об отношении приращений двух функций). Если функции y = f(x) и y= g(x) 1)непрерывны на отрезке [a;b] ; 2)дифференцируемы на интервале (a;b) ; 3)производная g′(x) ≠ 0 на интервале(a;b) . Тогда на интервале (a;b) найдется по крайней мере одна точка x0 такая что 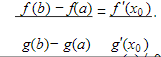 Основные теоремы дифференциального исчисления. Теорема Лопиталя.  Монотонность функции. Необходимый и достаточный признаки возрастания (убывания) функции. Моното́нная фу́нкция — это функция, приращение которой не меняет знака, то есть либо всегда неотрицательное, либо всегда неположительное. Определение 1. Функция f называется возрастающей на промежутке X, если для любых Определение 2. Функция f называется убывающей на промежутке X, если для любых |
