функция одной переменной. Функция одной переменной. Функция одной переменной. Основные определения. Способы задания функций. Основные элементарные функции

Название	Функция одной переменной. Основные определения. Способы задания функций. Основные элементарные функции
Анкор	функция одной переменной
Дата	23.03.2023
Размер	0.54 Mb.
Формат файла
Имя файла	Функция одной переменной.docx
Тип	Документы #1011230
страница	3 из 3

1 2 3

Теорема 1. (условие возрастания функции). Пусть функция :

1) определена и непрерывна на промежутке X;

2) во всех внутренних точках промежутка X производная .

Тогда функция f возрастает на промежутке X.

Теорема 2. (условие убывания функции). Пусть функция :

1) определена и непрерывна на промежутке X;

2) во всех внутренних точках промежутка X производная .

Тогда функция f убывает на промежутке X.

Необходимый и достаточный признаки возрастания (убывания) функции.

Определение возрастающей функции. Функция y = f(x) возрастает на интервале X, если для любых

выполняется неравенство

. Другими словами – большему значению аргумента соответствует большее значение функции. Определение убывающей функции. Функция y = f(x) убывает на интервале X, если для любых

выполняется неравенство

. Другими словами – большему значению аргумента соответствует меньшее значение функции.

Достаточные признаки возрастания и убывания функции.

На основании достаточных признаков находятся промежутки возрастания и убывания функции. Вот формулировки признаков:

*)если производная функции y = f(x) положительна для любого x из интервала X, то функция возрастает на X;

*)если производная функции y = f(x) отрицательна для любого x из интервала X, то функция убывает на X.

Таким образом, чтобы определить промежутки возрастания и убывания функции необходимо:

*)найти область определения функции;

*)найти производную функции;

*)решить неравенства

на области определения;

*)к полученным промежуткам добавить граничные точки, в которых функция определена и непрерывна.

Локальный экстремум Необходимый и достаточный признаки существования локального экстремума.

Экстре́мум — максимальное или минимальное значение функции на заданном множестве. Соответственно, если достигается минимум — точка экстремума называется точкой минимума, а если максимум — точкой максимума.

Необходимые условия существования локальных экстремумов

Если дифференцируемая функция у = f(x) имеет экстремум в точке, то ее производная в этой точке равна нулю: f'(x0 ) =О.

Если в точке экстремума существует первая частная производная (по какому-либо аргументу), то она равна нулю.

Теорема (достаточное условие экстремума). Если непрерывная функция у = f(x) дифференцируема в некоторой д-окрестности критической точки 0 и при переходе через нее (слева направо) производная f'(x) меняет знак с плюса на минус, то 0 есть точка максимума; с минуса на плюс, то 0 - точка минимума.

Первое достаточное условие локального экстремума

Теорема 1 (первое достаточное условие локального экстремума). Пусть функция

определена на

_{и дифференцирована на этом интервале везде за исключением, возможно, точки , но в этой точке функция является непрерывной. Если существуют такие правая и левая полуокрестности точки , в каждой из которых сохраняет определенный знак, то}

_{1) функция имеет локальный экстремум в точке , если принимает значения разных знаков в соответствующих полуокрестностях;}

_{2) функция не имеет локальный экстремум в точке , если справа и слева от точки имеет одинаковый знак.}

Теорема 2 (второе достаточное условие локального экстремума). Пусть функция

определена на

_{, , и выполняются условия:}

_{1. ;}

_{2. существует ,}

_{тогда имеет локальный экстремум в точке , а именно}

_{локальный максимум, если ;}
_{локальный минимум, если .}

_{Второе достаточное условие является частным случаем третьего достаточного условия локального экстремума.}

_{Теорема 3 (третье достаточное условие локального экстремума)}_.Пусть функция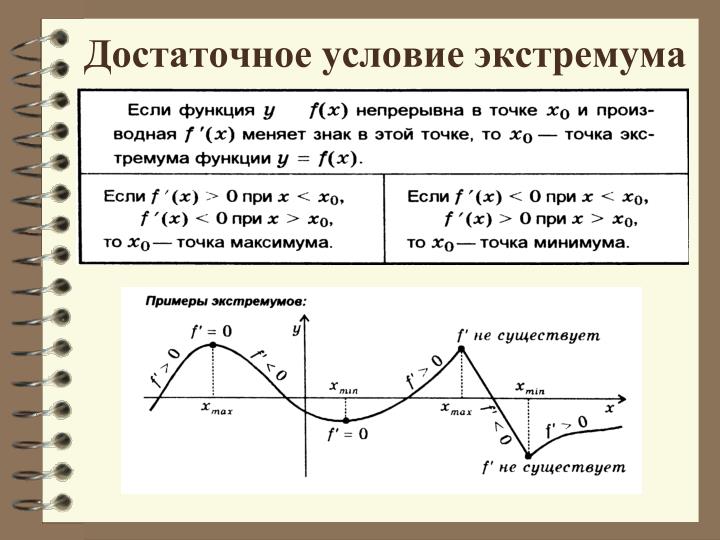

определена на

_{, раз дифференцирована в точке , и выполняются условия (1). Тогда если - четное, то имеет локальный экстремум в точке (локальный максимум, когда , локальный минимум, когда ). Если - нечетное, то экстремума в точке нет.}

Глобальный экстремум

Функция

имеет в точке

глобальный максимум или глобальный минимум если неравенство

или

соответственно выполнено для всех точек Х из этой области

Терема Вейерштрассе: Если область

замкнута и ограниченна, то дифференцируемая функция

достигает в этой области своих наибольшего и наименьшего значений в стационарной точке или в граничной точке области.

Алгоритм нахождения глобального экстремума

Найти все стационарные точки функции в области и вычислить значение функции в них.
Исследовать функцию на экстремум на границе области .
Сравнить значения функций п.1 и п.2 и выбрать из них максимальное и минимальное.

Применение второй производной: «второй достаточный признак существования локального экстремума.

Теорема (Достаточное условие выпуклости (вогнутости) графика функции). Пусть функция дважды дифференцируема на интервале. Если ƒ′′(х) <0 на (a;b), то график функции выпуклый на (a;b); если ƒ′′(х)>0 на (a;b), то график функции вогнутый на (a;b).

Теорема (Достаточное условие точки перегиба). Если вторая производная дважды дифференцируемой функции при переходе через критическую точку второго рода х₀ меняет знак, то х₀ есть абсцисса точки перегиба графика этой функции.
Если в окружении точки

вторая производная непрерывная, причем

, а

, то функция

имеет в точке

максимум, когда

, и минимум, когда

Направление выпуклости графика функции. Достаточный признак выпуклости графика функции вверх (вниз).

Определение.График функции имеет на интервале

выпуклость, направленную вниз (вверх), если график этой функции в пределах указанного интервала лежит не ниже (не выше) любой своей касательной.

Теорема 9.4.Если функция имеет на интервале

конечную вторую производную и если эта производная неотрицательна (неположительна) всюду на этом интервале, то график функции имеет на интервале

выпуклость, направленную вниз (вверх).

Точки перегиба графика функции. Достаточный признак существования точки перегиба.

Определение. Точка графика непрерывной функции f(x), при переходе через которую кривая меняет направление выпуклости, называется точкой перегиба.

Теорема 1 (необходимое условие существования точки перегиба). Если функция у = f(x) имеет непрерывные производные до второго порядка включительно на интервале ]а; b[ и точка (х₀; f (х₀)), где х_о

]а;b[, является точкой перегиба графика функции f(x), то

Теорема 2 (достаточное условие). Если функция y=.f(x), x

]a; b[, дважды дифференцируема на интервале ]а; b[ и при переходе через х_о]а; b[ вторая производная f"(x) меняет знак, то точки кривой с абсциссой х — х₀ является точкой перегиба.

Асимптоты графика функции.

Определение.

Асимптотой кривой называется прямая, расстояние до которой от точки, лежащей на кривой, стремится к нулю при неограниченном удалении от начала координат этой точки по кривой (рис.5.10).

Асимптоты бывают вертикальные (параллельные оси Оу), горизонтальные (параллельные оси Ох) и наклонные.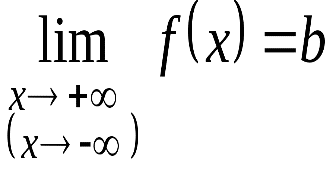

Прямая