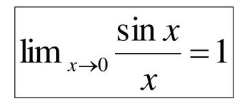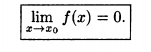Функция одной переменной. Основные определения. Способы задания функций. Основные элементарные функции.
Числовая последовательность. Предел числовой последовательности. Теоремы о пределе последовательности.
Предел функции. Теоремы о пределах функции.
Непрерывность функции в точке. Предел функции, непрерывной в точке.7
Первый замечательный предел.
Второй замечательный предел.
Бесконечно малые функции. Свойства бесконечно малых функций.
Сравнение бесконечно малых функций. Эквивалентные бесконечно малые функции. Таблица эквивалентностей.
Точки разрыва функции. Классификация точек разрыва.
Непрерывность функции на отрезке. Основные теоремы о функциях, непрерывных на отрезке.
Задачи, приводящие к понятию производной.
Определение производной. Связь между непрерывностью и дифференцируемостью функции.
Основные правила дифференцирования.
Производные основных элементарных функций.
Дифференцирование сложной функции.
Дифференцирование параметрически заданных функций.
Дифференцирование неявно заданных функций.
Логарифмическое дифференцирование. Дифференцирование показательно-степенных функций.
Дифференциал функции. Геометрический смысл дифференциала. Свойства дифференциала. Применение дифференциала к приближенным вычислениям.
Производные и дифференциалы высших порядков.
Уравнения касательной нормали к кривой.
Основные теоремы дифференциального исчисления. Теорема Ферма.
Основные теоремы дифференциального исчисления. Теорема Ролля. .
Основные теоремы дифференциального исчисления. Теорема Лагранжа.
Основные теоремы дифференциального исчисления. Теорема Коши.
Основные теоремы дифференциального исчисления. Теорема Лопиталя.
Монотонность функции. Необходимый и достаточный признаки возрастания (убывания) функции.
Локальный экстремум Необходимый и достаточный признаки существования локального экстремума.
Глобальный экстремум).
Применение второй производной: «второй достаточный признак существования локального экстремума.
Направление выпуклости графика функции. Достаточный признак выпуклости графика функции вверх (вниз).
Точки перегиба графика функции. Достаточный признак существования точки перегиба.
Асимптоты графика функции.
Функция одной переменной. Основные определения. Способы задания функций. Основные элементарные функции.
Определение функции.
Возьмем некоторое множество значений величины х, т. е. некоторое множество точек на числовой оси Ох, и обозначим его через D. Если каждому значению х из множества D по какому-нибудь правилу поставлено в соответствие одно определенное значение другой величины у, то говорят, что эта величина у есть функция величины х или что величины х и у связаны между собой функциональной зависимостью.
Определение функции.
Величина у называется функцией переменной величины х в области определения D, если каждому значению х из этой области соответствует одно определенное значение величины у.
Способы задания функций (таблицей, формулой и графиком)
Задать функцию — это значит указать область ее определения и правило, при помощи которого по данному значению независимой переменной находятся соответствующие ему значения функции
Табличное задание.
При табличном задании просто выписывается ряд значений независимой переменной и соответствующих им значений функции
Аналитическое задание (задание формулой).
Аналитическое задание функции состоит в том, что дается формула, с помощью которой по заданным значениям независимой переменной можно получать соответствующие им значения функции.
Графическое задание
Определение. Графиком функции (в системе декартовых прямоугольных координат) называется множество всех точек, абсциссы которых являются значениями независимой переменной, а ординаты — соответствующими значениями функции.
Основные элементарные функции:
Степенная
у = хn
Показательная
y=ax
Логарифмическая
y=Logax
Тригонометрическая
y=sin x y=cos x, y=tg x, y=ctg x
Обратная тригонометрическая
у = arcsin x, у = ягссоs x, y=arctg x, y=arcctg x
2. Числовая последовательность. Предел числовой последовательности. Теоремы о пределе последовательности.
Числовая последовательность
Под числовой последовательностью х1,х2…хn понимается функция xn=f(n) заданная на множестве N натуральных чисел
Предел числовой последовательности
Число а называется пределом последовательности {xn}, если для любого положительного числа ε найдется такое натуральное число N, что при всех n > N выполняется неравенство
|xn-a|<ε
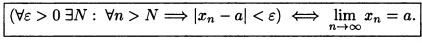
Теоремы о пределе последовательности.
1. Последовательность может иметь только один предел.
2. Последовательность, имеющая конечный предел, ограниченная; последовательность, имеющая бесконечный предел, неограниченная.
3. Необходимый и достаточный признак существования предела последовательности. Для того, чтобы последовательность 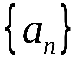 имела предел, необходимо и достаточно, чтобы при задании любого как угодно малого положительного числа имела предел, необходимо и достаточно, чтобы при задании любого как угодно малого положительного числа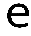 можно было указать такой ее член можно было указать такой ее член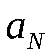 , что любые два члена, стоящие после , что любые два члена, стоящие после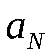 , будут отличаться друг от друга на число, меньшее , будут отличаться друг от друга на число, меньшее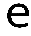 , т. е. , т. е.
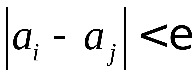 при при 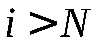 и и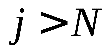
Предел функции. Теоремы о пределах функции.
Определение. Число А называется пределом функции y=f(x) при х—>х0 , если для всех значений х, достаточно мало отличающихся от числа х0 , соответствующие значения функции f(x) как угодно мало отличаются от числа А.
Теорема 1. (о предельном переходе в равенстве) Если две функции принимают одинаковые значения в окрестности некоторой точки, то их пределы в этой точке совпадают.
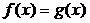 Þ Þ 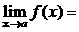 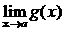 . .
Теорема 2. (о предельном переходе в неравенстве) Если значения функции f(x) в окрестности некоторой точки не превосходят соответствующих значений функции g(x) , то предел функции f(x) в этой точке не превосходит предела функции g(x).
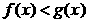 Þ Þ 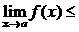 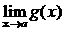 . .
Теорема 3. Предел постоянной равен самой постоянной.
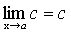 . .
Теорема 4. Функция не может иметь двух различных пределов в
одной точке.
Теорема 5. Если каждое слагаемое алгебраической суммы функций имеет предел при  , то и алгебраическая сумма имеет предел при , то и алгебраическая сумма имеет предел при , причем предел алгебраической суммы равен алгебраической сумме пределов. , причем предел алгебраической суммы равен алгебраической сумме пределов.
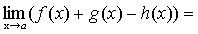 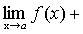 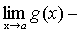 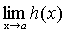 . .
Теорема 6. Если каждый из сомножителей произведения конечного числа функций имеет предел при  , то и произведение имеет предел при , то и произведение имеет предел при , причем предел произведения равен произведению пределов. , причем предел произведения равен произведению пределов.
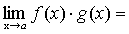 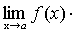 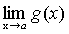 . .
Следствие. Постоянный множитель можно выносить за знак предела.
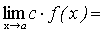 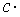 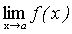 . .
Теорема 7. Если функции f(x) и g(x) имеют предел при  , ,
причем 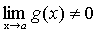 , то и их частное имеет предел при , то и их частное имеет предел при , причем предел частного равен частному пределов. , причем предел частного равен частному пределов.
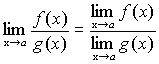 , , 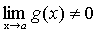 . .
Непрерывность функции в точке. Предел функции, непрерывной в точке.
Определение
Функция у =/(х) называется непрерывной в точке х0 , если эта функция определена в какой-нибудь окрестности точки х0 и если 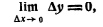 т. е. если бесконечно малому приращению аргумента соответствует бесконечно малое приращение функции. т. е. если бесконечно малому приращению аргумента соответствует бесконечно малое приращение функции.
Предел функции, непрерывной в точке.
Функция y = f(x) называется непрерывной в точке х = а, если существует предел функции в этой точке, т.е.
Функция y = f(x) будет непрерывной в точке х = а тогда и только тогда, когда выполняются условия:
функция y = f(x) определена в точке х = а, т.е. существует f(a);
существует предел lim х→а f(x) функции в точке х = а;
предел функции в точке х = а равен значению функции в этой точке, т.е.
lim х→а f(x) = f(a).
Первый замечательный предел.
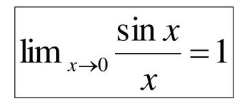
Второй замечательный предел.

Бесконечно малые функции. Свойства бесконечно малых функций.
Функция у = f(x) называется бесконечно малой при х -> , если
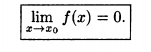
Свойства бесконечно малых функций
1. Алгебраическая сумма конечного числа б.м.. есть б.м.
2. Произведение ограниченной функции на бесконечно малую функцию есть функция бесконечно малая.
3. Частное от деления б.м., предел которой отличен от 0, есть б.м.
Сравнение бесконечно малых функций. Эквивалентные бесконечно малые функции. Таблица эквивалентностей.
Эти бесконечно малые функции можно сравнивать по быстроте их убывания, т.е. по быстроте их стремления к нулю.
Определение. Если 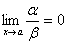 , то функция называется бесконечно малой более высокого порядка, чем функция . , то функция называется бесконечно малой более высокого порядка, чем функция .
Определение. Если 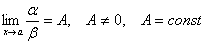 , то и называются бесконечно малыми одного порядка. , то и называются бесконечно малыми одного порядка.
Определение. Если 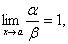 то функции и называются эквивалентными бесконечно малыми. Записывают то функции и называются эквивалентными бесконечно малыми. Записывают .
Определение. Бесконечно малая функция называется бесконечно малой порядка k относительно бесконечно малой функции , если предел 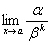 конечен и отличен от нуля. конечен и отличен от нуля.
Однако следует отметить, что не все бесконечно малые функции можно сравнивать между собой. Например, если отношение 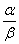 не имеет предела, то функции несравнимы. не имеет предела, то функции несравнимы.
1)
, 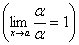
2) Если
и
, то
, 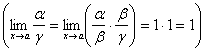
3) Если
, то
, 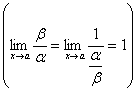
4) Если
1 и
1 и 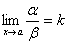 , то и , то и 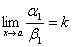 или или 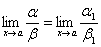 . .
Точки разрыва функции. Классификация точек разрыва.
Определение. Точка х0 называется точкой разрыва функции f(x), если f(x) не определена в точке х0 или не является непрерывной в этой точке
|
 Скачать 0.54 Mb.
Скачать 0.54 Mb.
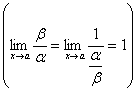

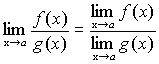 ,
,