Стальные конструкции одноэтажного промышленного здания в городе Н. Новгород. ПЗ МК 51. Г аоу ао во астраханский государственный архитектурностроительный университет

• Название: Г аоу ао во астраханский государственный архитектурностроительный университет
• Анкор: Стальные конструкции одноэтажного промышленного здания в городе Н. Новгород
• Дата: 30.03.2022
• Размер: 1.03 Mb.
• Имя файла: ПЗ МК 51.doc
• Тип: Пояснительная записка; #429808
• страница: 13 из 15

6 Расчет колонны

6. 1 Расчетные длины  

Проверка возможности применения данных табл. 18 СНиП II-23

Сочетание нагрузок, дающее наибольшие значения продольных сил, 1 2 3 -5 7.

Сжимающее продольное усилие для нижней части колонны N_н =2011.9 кН.

Сжимающее продольное усилие в верхней части колонны N_в =451.6 кН.

Длина нижней части колонны       Н_н = 16230 мм.

Длина верхней части колонны Н_в = 6370 мм.

Высота подкрановой балки Н_пб = 1000 мм.

Условия применения решения табл. 18 СНиП II-23:

допустимое отношение продольных сил N_н / N_в> = 3  

проверка: N_н / N_в = 2011.9 / 451.6 = 2011.9 / 451.6 = 4.46 > 3 (выполнено) 

допустимое отношение длин частей колонн l_в / l_н <= 0.6.

проверка: l_в / l_н = 6370 / 16230 = 6370 / 16230 = 0.392 < 0.6  (выполнено) 

Отношение моментов инерции J_в / J_н = 1260000 / 11300000 = 0.112;  

Коэффициенты приведения длины приняты по табл. 18 для случая "свободный конец" : 

• 
  для нижнего участка m_н = 2.5;
  
• 
  для верхнего участка m_в =3.    
  

Расчетная длина в плоскости рамы:  

для нижней части колонны  

l^x_ef,н = _н * H_н =2.5 * (0.1 * 16230) = 4057.5 см;

для верхней части колонны  

l^x_ef,в = _в * H_в =3 * (0.1 * 6370) = 1911 см;

Расчетная длина из плоскости равна расстоянию между закреплениями

для нижней части колонны  

l^y_{ef, н} = Н_н = 0.1 * 16230 = 1623 см;

для верхней части колонны  

      l^y_{ef, в} = Н_в - Н_пб = 0.1 * (6370 - 1000) = 537 см.

6.2. Подбор сечения верхней части колонны

Исходные данные, полученные на предыдущих этапах расчета    

Коэффициент условий работы _с =1.00.

Неблагоприятное сочетание усилий — в сочетании 1 3 6 8.  

Расчетное сочетание усилий для верхней части колонны в верхнем сечении

N= 288.00 кН; M= 417 кНм,

в том же сочетании нагрузок в нижнем сечении M= 94.00 кНм.

Сечение двутавровое, симметричное, заданная высота сечения 70 см.

Сталь С245. При толщине листового проката t = 20 мм, расчетное сопротивление  

R_y =240 мПа = 24.00 кН/см².

6.2.1 Компоновка сечения

Предварительное определение требуемой площади сечения                  

Предварительно требуемая площадь сечения определена по формуле

[A] = N / (R_y*_e * _c ),

где _e — коэффициент продольного изгиба сплошного стержня при внецентренном сжатии

Расчет _e

Эксцентриситет продольной силы e_x =M /N = 417 / 288 = 1.45 м = 144.79 см.

Радиус инерции для симметричного двутавра i_x ≈ 0,42b_в = 0.42 * 70 = 29.4 см.

Условная гибкость элемента в плоскости рамы   _x= L_в / i_x* √ (R_y / E) = 2.22.  

Радиус ядра сечения ρ_x ≈ 0,35 * b_в =0.35 * 70 = 24.5 см;

относительный эксцентриситет m_x = е_х / _x =144.79 / 24.5 = 5.910;

коэффициент влияния формы сечения (предварительно)  = 1.2.

Приведенный относительный эксцентриситет m_efx = η * m_x1.2 * 5.91 = 7.09.

Коэффициент продольного изгиба сплошного стержня при внецентренном сжатии, по табличным данным норм, _e =0.163.  

Требуемая площадь сечения  

[A] = N / (R_y*_e * _c ) =288 / (24 * 0.163 * 1) = 73.62 см².

Предварительно принята толщина полки 1.2 см.


Выбор толщины стенки с учетом местной устойчивости    

При заданной толщине полки, высота стенки двутавра
h_w = b_в – 2 * t_f = 70 - 2 * 1.2 = 67.6 см.

Проверка условия местной устойчивости стенки  по формуле

h_w / t_w <= _uw * (E / R_y) 

где расчет _uw выполнен по табл. 27 [3] для двутаврового сечения, при значении относительного эксцентриситета m = m_x = 5.910.

При m >=1 приведенная гибкость принята в плоскости действия момента,  = 2.22.

Так как  >2, _uw = 1.2 + 0.35 *  = 1.2 + 0.35 * 2.22 = 1.977;

Учитывая m = 5.910, предельная гибкость _uw=1.977.

Толщина стенки из условия местной устойчивости  

[t_w]= 67.6 * (24 / 20600)^(1/2) / 1.977 = 1.17 см.

Толщина стенки принята t_w = 0.8 см, менее требуемой по условию местной устойчивости,  

при этом в расчете устойчивости учтена только устойчивая часть стенки [4] . Длина устойчивой части стенки  (два крайних участка, примыкающих к полке)

h_w1 = 2 * 0,85 * t _w*√ (E /Ry) = 2 * 0.85 * 0.8 * (20600 / 24)^(1/2) = 39.84 см.

Обоснование ширины полки

Требуемая по условию A_в^тр площадь полки

А_f = (A_в^тр – t _w * h_w1) / 2 =(73.62 - 0.8 * 39.84) / 2 = 20.87 см².

соответственно, ширина полки b_f должна быть не менее A_f / t_f =20.87 / 1.2 = 17.39 см.

По конструктивному правилу устойчивости верхней части колонны из плоскости рамы

момента ширина полки должна быть не менее (0.1 * 6370) / 20 = 31.85 см.

Принята ширина полки b_f = 32 см;

Проверка устойчивости свеса полки   выполнена по правилам по табл. 29* [3]

b_ef / t <= (0.36 + 0.10)* (E / R_y) 

Свес полки b_ef =0.5 * (32 - 0.8) = 15.6 см:

условная гибкость элемента в плоскости рамы  =2.22  

Проверка

b_ef / t = 13.00 < [b_ef/ t ] = (0.36 + 0.1 * 2.22) * (20600 / 24)^(1/2) = 17.05;

Расхождение % =23.75% с избытком.

6.2.2 Расчёт геометрических характеристик составного сечения                  

Относительно оси x - x  

высота сечения балки h = 70 см

высота стенки 70 - 2 * 1.2 = 67.6 см;

расстояние до ц.т. пояса y^f_цт =(70 / 2 - 1.2 / 2) = 34.4 см;

полная площадь сечения A = 67.6 * 0.8 + 2 * (32 * 1.2) = 130.88 см²;

приведенная площадь сечения 39.84 * 0.8 + 2 * (32 * 1.2) = 108.672 см²;

принято при проверке устойчивости A_red = MIN(130.88, 108.672) = 108.67 см²;

момент инерции сечения  

J_x = 2 * (b_f * t_f³/ 12 + b_f * t_f * y^f_цт²) + t_w * h_w ³/12 =  

2 * (32 * 1.2^3 / 12 + 32 * 1.2 * 34.4^2) + 0.8 * 67.6^3 / 12 = 111486 см⁴;

момент сопротивления W_x = 111486 / (0.5 * 70) = 3185 см³;

радиус инерции i_x = √(I_x /А) = (111486 / 130.88)^(1/2) = 29.19 см;

радиус ядра сечения r _x = W_x/ A =3185 / 130.88 = 24.34 см.

Относительно оси у-у  

момент инерции сечения J_y = 2 * t_f * b_f³/ 12 + h_w * t_w³/ 12 = 

2 * 1.2 * 32^3 / 12 + 67.6 * 0.8^3 / 12 = 6556.5 см⁴;

радиус инерции i_y = √(I_y / А)=(6556.5 / 130.88)^(1/2) = 7.08.

Расчет гибкости стержня                  

Гибкость стержня _x = L_x^в / i_x =1911 / 29.19 = 65.47;

условная гибкость _x = l_x* √ (R_y / E) =65.47 * (24 / 20600)^(1/2) = 2.23.

Гибкость стержня _y = L_y^в / i_y =537 / 7.08 = 75.85;

условная гибкость     _y= _y* (R_y / E) =75.85 * (24 / 20600)^(1/2) = 2.59.

6.2.3 Проверка устойчивости верхней части колонны в плоскости действия момента

Предельное неравенство устойчивости стержня в плоскости действия момента  

σ_х = N/( φ_е' * A) ≤ R_y _c  

Проверка по правилам [3].  

e_x = 100 * 417 / 288 = 144.79 см;

m_x = e_x /_x =144.79 / 24.34 = 5.95;

A_f / A_w = 32 * 1.2 / (67.6 * 0.8) = 0.71;

При A_f/A_w 0.71 и  =2.23 и m = 5.95,  

коэффициент влияния формы сечения  =1.29.

При m_ef = m_x* η = 5.95 * 1.29 = 7.68, коэффициент продольного изгиба сплошного стержня при внецентенном сжатии φ_е = 0.154.

Условие устойчивости в плоскости действия момента выполнено  

σ_х = N / ( φ_е' * A) = 288 / (0.154 * 108.67) = 17.21 кН/см²;

σ_х = 17.21 < R_y* γ_c =24 * 1 = 24 кН/см²..

Расхождение % =28.3%  

6.2.4 Проверка устойчивости верхней части колонны из плоскости действия момента

Предельное неравенство устойчивости стержня из плоскости действия момента  

σ = N_max / (c * φ_y * A) ≤ R_y * γ_c.  

Проверка по правилам [3].  

Длина участка между закрепленными из плоскости узлами  

l =(6370 - 1000) = 5370 мм.

При расчете устойчивости из плоскости принимают максимальный момент в средней  

трети расчетной длины стержня из плоскости  

M = 94 + (417 - 94) / 6370 * (6370 - 5370 / 3) = 326.24 кНм

Коэффициенты продольного изгиба  

При _{y =}2.59, _y = 0.718;

При _c = 3.14 * (20600 / 24)^(1/2) = 91.994, _с = 0.597.

Определение коэффициента с

При mx <= 5.00, расчетная формула

с = /(1 +  * m_x)  

 = 0.65 + 0.05 * 5 = 0.900;

√(_c /_y) =(0.597 / 0.718)^(1/2) = 0.912;

 =  1;

с₅ = / (1 +  * m_x) =1 / (1 + 0.9 * 5) = 0.1818.

При mx >= 10.00, расчетная формула

с = 1/(1 + m_x * _y /_b)  

Определение _b —по табл. 78  [3]

h = 67.6 + 2 * 1.2 = 70 см

l_ef = 0.1 * 5370 = 537 см

 = 8 [(l_ef * t₁) / (h * b_f)] ^2 * [ 1 + (0.5 * h) * t^3 / (b_f * t₁^3)] = 

8 * ( 537 * 1.2 / (70 * 32)) ^2 * ( 1 + (0.5 * 70) * 0.8^3 / (32 * 1.2^3)) = 0.877;

= 1.42 * √=1.42 * 0.877^(1/2) = 1.330;

₁ =  * J_y / J_x *(h / l_ef)² * E / R_y =
1.33 * 6556.5 / 111486 * (70 / 537)^2 * 20600 / 24 = 1.141.

_b = 0.68 + 0.21₁ = 0.68 + 0.21 * 1.141 = 0.920;

с₁₀ = 1/(1 + m_x * _y /_b) = 1 / (1 + 10 * 0.718 / 0.92) = 0.114  

Так как 5 < m_x <10, значение коэффициента с принято по интерполяции  

c = 0.1818 * (2 - 0.2 * 5.95) + 0.114 * (0.2 * 5.95 - 1) = 0.169.

Условие устойчивости из плоскости действия момента выполнено   

σ = N_max/(c * φ_y * A) ≤ R_y * γ_c.  

σ = 288 / (0.169 * 0.718 * 108.67) = 21.84 < 24 * 1 = 24 кН/см².

Расхождение % =9.0%   с избытком.   

Принятое сечение верхней части колонны см. на рис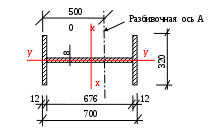. 6.1    
Рисунок 6.1