учебник по ахд. учебник по АХД. Г. В. Савицкая Анализ хозяйственной деятельности предприятия
 Скачать 7.77 Mb. Скачать 7.77 Mb.
|
|
Важной проблемой при прогнозировании эффективности инвестиционных проектов является рост цен в связи с инфляцией. В условиях инфляции для дисконтирования денежных потоков нужно применять не реальную, а номинальную ставку доходности. Чтобы понять методику учета инфляции, необходимо выяснить разницу между реальной и номинальной ставкой дохода. Зависимость между реальной и номинальной ставкой дохода можно выразить следующим образом: (1 + r)(l + m) = 1 + d, d = (1 + r)(l + т) – 1, где r - необходимая реальная ставка дохода (до поправки на инфляцию); т - темп инфляции, который обычно измеряется индексом розничных цен; d - необходимая денежная ставка дохода. Предположим, инвестор имеет 1 млн. руб., который он желает вложить так, чтобы ежегодно его состояние увеличивалось на 20%. Допустим, что темп инфляции 50% в год. Если инвестор желает получить реальный доход 20% на свой капитал, то он обязан защитить свои деньги от инфляции Денежная (номинальная) ставка дохода, которая нужна инвестору для получения реального дохода в 20% и защиты от инфляции в 50%, составит: d = (1 + 0,2) × (1 + 0,5) – 1= 0,8, или 80%. Зная номинальную (денежную) ставку доходности, можно определить реальную ставку по следующей формуле: Если затраты и цены растут одинаковыми темпами в соответствии с индексом инфляции, то в методах ДДП можно не учитывать инфляцию. Ситуация изменяется, если затраты и цены растут разными темпами. Тогда нельзя производить дисконтирование денежных поступлений, выраженных в постоянных ценах по реальной ставке дохода. Правильный метод - расчет фактических денежных поступлений с учетом роста цен и дисконтирования их по денежной ставке дохода. Пример 5. Предприятие решает, следует ли ему вкладывать средства в оборудование, стоимость которого 3,5 млн. руб. Это позволяет увеличить объем продаж на 6 млн. руб. (в постоянных ценах) на протяжении двух лет. Затраты составят 3 млн. руб. Реальная ставка дохода - 10%, темп инфляции - 50% в год. В случае реализации проекта цены на продукцию будут расти всего на 30%, а затраты - на 50% в год. Определим сначала необходимую денежную ставку дохода: (1,10 × 1,5) – 1 = 0,65, или 65 %, а также выручку, затраты и доход.
Рассчитаем текущую стоимость доходов.
Чистая текущая стоимость составляет 3,24 – 3,5 = -0,26 млн. руб. Результат отрицательный, следовательно, проект невыгодный для предприятия. Если бы мы в этом случае применили реальную ставку дохода 10% к денежным поступлениям в текущих ценах, то допустили бы ошибку.
Чистая текущая стоимость доходов в этом случае будет больше нуля и составит 5,2 – 3,5 = +1,7 млн. руб. Это неправильный результат. Таким образом, с помощью метода чистой текущей стоимости (чистого приведенного эффекта) можно довольно реально оценить доходность проектов. Этот метод используется в качестве основного при анализе эффективности инвестиционной деятельности, хотя это не исключает возможности применения и других методов. Важным показателем, используемым для оценки и прогнозирования эффективности инвестиций, является индекс рентабельности, основанный на дисконтировании денежных поступлений. Расчет его производится по формуле В отличие от чистой текущей стоимости данный показатель является относительным, поэтому его удобно использовать при выборе варианта проекта инвестирования из ряда альтернативных.
По величине NPV наиболее выгоден проект С, а по уровню индекса рентабельности - проект А. Очень популярным показателем, который применяется для оценки эффективности инвестиций, является внутренняя норма доходности (IRR).Этота ставка дисконта, при которой дисконтированные доходы от проекта равны инвестиционным затратам. Внутренняя норма доходности определяет максимально приемлемую ставку дисконта, при которой можно инвестировать средства без каких-либо потерь для собственника. Ее значение находят из следующего уравнения: Экономический смысл данного показателя заключается в том, что он показывает ожидаемую норму доходности или максимально допустимый уровень инвестиционных затрат в оцениваемый проект. IRR должен быть выше средневзвешенной цены инвестиционных ресурсов: IRR > СС. Если это условие выдерживается, инвестор может принять проект, в противном случае он должен быть отклонен. Для нахождения IRR можно использовать финансовые функции программы калькуляции электронной таблицы Excel или финансового калькулятора. При отсутствии возможности их использования определить его уровень можно методом последовательной итерации, рассчитывая NРV при различных значениях дисконтной ставки (r) до того значения, пока величина NPVпримет отрицательное значение, после чего значение IRR находят по формуле При этом должны соблюдаться следующие неравенства: ra< IRR < rb, а NРVa > 0 > NРVb . Пример 6. Требуется найти значение IRR для проекта стоимостью 5 млн. руб., который будет приносить доход в течение четырех лет по 2 млн. руб. ежегодно. Возьмем произвольно два значения ставки дисконтирования (r = 20% и r = 25%) и рассчитаем текущую стоимость доходов (табл. 23.5). Таблица 23.5 Расчет исходных данных для определения IRR
На основании полученных данных найдем значение IRR для рассматриваемого проекта по приведенной выше формуле: IRR = 20% + (25% – 20%) × Точность вычислений IRR зависит от интервала между rаи rb. Чем меньше длина интервала между минимальным и максимальным значением ставки дисконтирования, когда функция меняет знак с «+» на «-» , тем точнее величина IRR Рассчитаем уточненное значение IRR при длине интервала равном 1%: rа = 21,5% и rb= 22,5%.
IRR = 21,5% + (22,5% – 21,5%) × При такой ставке текущие доходы по проекту будут равны инвестиционным затратам. Чтобы сделать вывод об эффективности проекта, необходимо полученное значение IRR сравнить с требуемым уровнем доходности. Если требуемый уровень доходности для данного проекта составляет 20% годовых, то можно сделать позитивное заключение о выгодности инвестирования в него средств. Внутреннюю норму доходности можно найти и графическим методом, если рассчитать NРV для всех ставок дисконтирования от нуля до какого-либо разумного большого значения (рис. 23.1). По горизонтальной оси откладывают различные ставки дисконтирования, а по вертикальной оси - соответствующие им значения NРV. График пересечет горизонтальную ось, где NРV= 0, при ставке дисконтирования, которая и является внутренней нормой доходности. 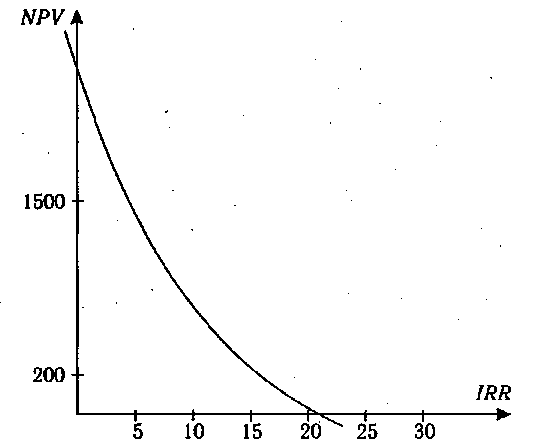 Рис. 23.1. График NPV инвестиционного проекта Показатели NPV и IRRвзаимно дополняют друг друга. Если NPV измеряет массу полученного дохода, то IRR оценивает способность проекта генерировать доход с каждого рубля инвестиций. Высокое значение NРV неможет быть единственным аргументом при выборе инвестиционного решения, так как оно во многом зависит от масштаба инвестиционного проекта и может быть связано с достаточно высоким риском. Поэтому менеджеры предпочитают относительные показатели, несмотря на достаточно высокую сложность расчетов. Если имеется несколько альтернативных проектов с одинаковыми значениями NPV, IRR,то при выборе окончательного варианта инвестирования учитывается длительность инвестиций (duration). | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
