Микроэкономика. Галина Ростиславовна Вечканова, Григорий Сергеевич Вечканов Микроэкономика

• Название: Галина Ростиславовна Вечканова, Григорий Сергеевич Вечканов Микроэкономика
• Анкор: Микроэкономика
• Дата: 02.06.2022
• Размер: 2.57 Mb.
• Имя файла: mikrojekonomika_vechkanova-g_r-vechkanov-g_s_2010-208s.doc
• Тип: Документы; #565007
• страница: 12 из 57

Вопрос 11

Эффект замены и эффект дохода по Слуцкому и по Хиксу.

ОТВЕТ

Положение о разложении общего эффекта изменения цен на эффект замены и эффект дохода впервые выдвинул российский экономист, математик и статистик Евгений Евгеньевич Слуцкий (1880–1948). В 1915 г. он опубликовал в итальянском экономическом журнале статью «К теории сбалансированного бюджета потребителя». Эта статья была «открыта» в 30-х гг. английским экономистом, математиком и статистиком Р. Алленом. О приоритете научного исследования этой проблемы Е. Слуцким говорит английский экономист Дж. Хикс в своей работе «Стоимость и капитал»¹, в которой он указывает, что разработанная им в соавторстве с Р. Алленом теория поведения потребителя «принадлежит по существу Слуцкому, с той лишь оговоркой, что я совершенно не был знаком с его работой ни во время завершения своего собственного исследования, ни даже некоторое время после опубликования содержания этих глав в журнале «Экономика» Р. Алленом и мной».

Подходы Слуцкого и Хикса к определению реального дохода отличаются. По Хиксу, разные уровни денежного дохода, обеспечивающие один и тот же уровень удовлетворения, представляют одинаковый уровень реального дохода. По Слуцкому, только тот уровень денежного дохода, который достаточен для приобретения одного и того же набора или комбинации товаров, обеспечивает и неизменный уровень реального дохода.

Подход Хикса больше отвечает основным положениям порядковой теории. Подход Слуцкого дает возможность количественного решения проблемы на базе статистических данных.
Эффект замены и эффект дохода по Слуцкому

Графическая модель разложения общего эффекта изменения цены на эффект замены и эффект дохода по Слуцкому изображена на рис. 11.1.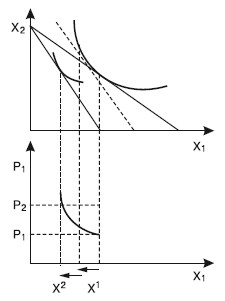


Рис. 11.1
На рис. 11.1 показаны нормальные (полноценные) блага, спрос на которые увеличивается при росте дохода. Исходя из этого при понижении реального дохода соответствующая компонента в уравнении Слуцкого отрицательна. Сумма двух отрицательных величин также отрицательна, поэтому общий итог повышения цены для нормальных благ состоит в уменьшении объема спроса на них. Влияние эффекта замены и эффекта дохода однонаправленно, что мы видим на рис. 11.1.

На рис. 11.2 показаны нейтральные блага. В том случае, когда потребитель считает данное благо нейтральным, при изменении дохода спрос на такое благо не изменяется, а эффект дохода равен нулю. Общее же изменение потребления этого блага совпадает с эффектом замены. В данном случае наклон кривой спроса будет более крутым в сравнении с наклоном кривой спроса на нормальное благо (см. рис. 11.1).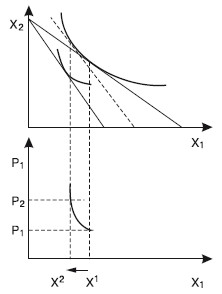


Рис. 11.2
На рис. 11.3 изображен график неполноценного блага, спрос на которое при росте дохода сокращается, однако абсолютная величина эффекта дохода меньше величины эффекта замены. Общий результат роста цены будет отрицательным, хотя он будет еще меньше по абсолютной величине, нежели в случае с нейтральными благами.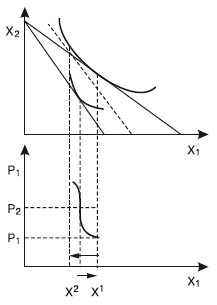


Рис. 11.3
В случае с неполноценным благом, когда эффект замены и эффект дохода равны по абсолютной величине, спрос на такое неполноценное благо будет абсолютно неэластичным (рис. 11.4).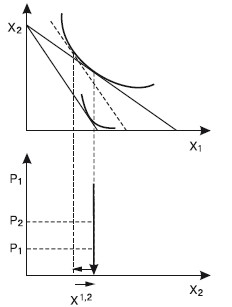


Рис. 11.4
В данном случае закон спроса продолжает действовать, однако его влияние нейтрализуется равносильным уменьшением реального дохода для неполноценных благ.

Когда же абсолютная величина эффекта дохода при изменении цены менее ценного блага превышает величину эффекта замены, то общий эффект повышения цены становится положительным.

Такой товар называется благом Гиффена, и кривая спроса на это благо имеет положительный наклон (рис. 11.5).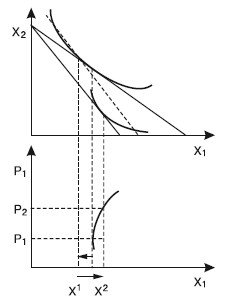


Рис. 11.5
Эффект замены и эффект дохода по Хиксу

Рассмотрим разделение общего эффекта изменения цены на эффект замены и эффект дохода по Хиксу на примере двух вариантов: а) в случае снижения цены; б) в случае повышения цены. Начнем с первого варианта.

Разложение общего эффекта изменения цены на эффект дохода и эффект замены иллюстрируется на рис. 11.6. Бюджетная линия KL соответствует денежному доходу I и ценам Рх и PY. Касание бюджетной линии кривой безразличия U1U1 в точке E1 характеризует оптимум потребителя, который отражает объем потребления благ X в количестве X 1. При неизменном денежном доходе I и при понижении X до РХ1 бюджетная линия займет положение KL1. Она касается более высокой кривой безразличия U2U2 в точке Е2, которой соответствует потребление блага X в объеме Х2. Следовательно, общий результат понижения цены блага X выражается в росте его потребления с X1 до Х2.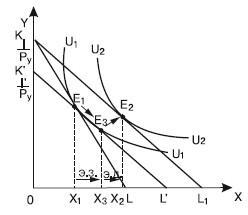


Рис. 11.6. Эффект замены и эффект дохода по Хиксу. Цена X снижается
Чтобы определить, каким должен был быть денежный доход потребителя для сохранения прежнего уровня удовлетворения при понижении цен, построим вспомогательную бюджетную линию K'L' (линия Хикса), параллельную линии KL1; которая одновременно является касательной к кривой безразличия U1U1 в точке Е3, соответствующей объему потребления блага Х3. При переходе от исходного к дополнительному оптимуму (от E 1 к Е3) реальный доход потребителя остается неизменным, оставаясь на прежней кривой безразличия UjUj. Таким образом, сдвиг от E1 к Е3 отражает эффект замены блага Y относительно подешевевшим благом X. Он равен разности Х3 – Х1; а эффект дохода составит Х2 – Х3. Действие эффекта дохода ведет к росту потребления обоих благ в точке Е2 в сравнении с точкой Е3.

Перейдем ко второму варианту разделения общего эффекта, когда цена блага X растет (рис. 11.7). Повышение цены вызывает перемещение оптимального положения потребителя на более низкую кривую безразличия U1U1. Общий эффект роста цены блага X состоит в сокращении его потребления с X 1 до Х2. В этом случае эффект замены составит X 1 – Х3, а эффект дохода – Х3 – Х2.

Следует отметить, что в обоих вариантах эффект замены показывается движением вдоль одной и той же кривой безразличия, а эффект дохода – перемещением с одной кривой безразличия на другую.

Эффект замены является всегда отрицательным: понижение цены одного блага стимулирует потребителей увеличивать его потребление, уменьшая потребление другого блага; повышение цены стимулирует потребителей замещать это благо другими, относительно подешевевшими.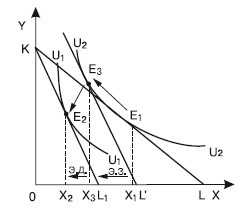


Рис. 11.7. Эффект замены и эффект дохода по Хиксу. Цена X повышается
Эффект дохода может быть отрицательным для полноценных благ, положительным – для неполноценных благ, нейтральным – когда спрос на благо при изменении дохода не изменяется и эффект дохода равен нулю.

Сопоставляя подходы Слуцкого и Хикса относительно деления общего эффекта на эффект замены и эффект дохода, можно сделать следующие выводы.

1. Методология Хикса допускает знание потребительских предпочтений, кривых безразличия, в то время как методология Слуцкого этого не требует, ибо она основывается на фактах поведения потребителей на рынке.

2. Методология Хикса соответствует основным положениям порядковой, или ординалистской, теории предельной полезности. Методология Слуцкого базируется на количественной, или кардиналистской, теории предельной полезности.

3. Слуцкий использовал менее строгий с точки зрения теории полезности, но более прагматичный метод определения данного уровня реального дохода.

4. По методологии Слуцкого, промежуточная бюджетная линия касается чаще всего более высокой, чем исходная, кривой безразличия, что и требуется по методологии Хикса. По Слуцкому, потребитель, располагая возможностью приобрести тот же набор благ, что и до изменения цен, окажется на более высоком уровне благосостояния, чем перед изменением цен.
СЛУЦКИЙ Евгений Евгеньевич (1880–1948), советский экономист, математик и статистик, основоположник математической теории потребления. На основе разработок зарубежных экономистов (В. Парето, Ф. Эджуорта и др.) связал функцию полезности, характеризующую предпочтения потребителей, с динамикой цен и размерами денежных доходов потребителей.

Образование получил в различных учебных заведениях. Сначала учился на математическом отделении Киевского университета, затем – на машиностроительном факультете Мюнхенского политехникума, а в 1911 г. закончил с золотой медалью юридический факультет Киевского университета.

Столь же разнообразна сфера его трудовой деятельности: профессор ряда вузов Киева, Конъюнктурный институт ЦСУ СССР (Москва), Научно-исследовательский институт математики и механики при МГУ, Математический институт им. В. А. Стеклова.