Альфа частицы. Где а и вэмпирические константы, L (ln 2)T1 Согласно
 Скачать 88.1 Kb.
|
Скорости вылетающих при распаде a-частиц очень велики и колеблются для разных ядер в пределах от 1,4×107 до 2×107 м/с, что соответствует энергиям от 4 до 8,8 МэВ. Согласно современным представлениям, a-частицы образуются в момент радиоактивного распада при встрече движущихся внутри ядра двух протонов и двух нейтронов. a-Частицы, испускаемые конкретным ядром, обладают, как правило, определенной энергией. Более тонкие измерения, однако, показали, что энергетический спектр a-частиц, испускаемых данным радиоактивным элементом, обнаруживает «тонкую структуру», т. е. испускается несколько групп a-частиц, причем в пределах каждой группы их энергии практически постоянны. Дискретный спектр a-частиц свидетельствует о том, что атомные ядра обладают дискретными энергетическими уровнями. Для a-распада характерна сильная зависимость между периодом полураспада T1/2 и энергией Е вылетающих частиц. Эта взаимосвязь определяется эмпирическим законом Гейгера - Нэттола (1912)*, который обычно выражают в виде зависимости между пробегом Ra (расстоянием, проходимым частицей в веществе до ее полной остановки) a-частиц в воздухе и постоянной радиоактивного распада l:  где А и В—эмпирические константы, l = (ln 2)/T1/2. Согласно формулы, чем меньше период полураспада радиоактивного элемента, тем больше пробег, а следовательно, и энергия испускаемых им a-частиц. Пробег a-частиц в воздухе (при нормальных условиях) составляет несколько сантиметров, в более плотных средах он гораздо меньше, составляя сотые доли миллиметра (a-частицы можно задержать обычным листом бумаги). Опыты Резерфорда по рассеянию a-частиц на ядрах урана показали, что a-частицы вплоть до энергии 8,8 МэВ испытывают на ядрах резерфордовское рассеяние, т. е. силы, действующие на a-частицы со стороны ядер, описываются законом Кулона. Подобный характер рассеяния a-частиц указывает на то, что они еще не вступают в область действия ядерных сил, т. е. можно сделать вывод, что ядро окружено потенциальным барьером, высота которого не меньше 8,8 МэВ. С другой стороны, a-частицы, испускаемые ураном, имеют энергию 4,2 МэВ. Следовательно, a-частицы вылетают из a-радиоактивного ядра с энергией, заметно меньшей высоты потенциального барьера. Классическая механика этот результат объяснить не могла. Объяснение a-распада дано квантовой механикой, согласно которой вылет a-частицы из ядра возможен благодаря туннельному эффекту — проникновению a-частицы сквозь потенциальный барьер. Всегда имеется отличная от нуля вероятность того, что частица с энергией, меньшей высоты потенциального барьера, пройдет сквозь вето, т. е., действительно, из a-радиоактивного ядра a-частицы могут вылетать с энергией, меньшей высоты потенциального барьера. Этот эффект целиком обусловлен волновой природой a-частиц. Вероятность прохождения a-частицы сквозь потенциальный барьер определяется его формой и вычисляется на основе уравнения Шредингера. В простейшем случае потенциального барьера с прямоугольными вертикальными стенками коэффициент прозрачности, определяющий вероятность прохождения сквозь него, определяется рассмотренной ранее формулой:  Анализируя это выражение, видим, что коэффициент прозрачности D тем больше (следовательно, тем меньше период полураспада), чем меньший по высоте (U) и ширине (l) барьер находится на пути a-частицы. Кроме того, при одной и той же потенциальной кривой барьер на пути частицы тем меньше, чем больше ее энергия Е. Таким образом качественно подтверждается закон Гейгера – Нэттола.
(A,Z) → (A−4, Z−2) + 4He. (2.1) Периоды полураспада известных α-радиоактивных ядер варьируются в широких пределах. Так, изотоп вольфрама 182W имеет период полураспада T1/2 > 8.3·1018 лет, а изотоп протактиния 219Pa имеет T1/2 = 5.3·10-8 c. 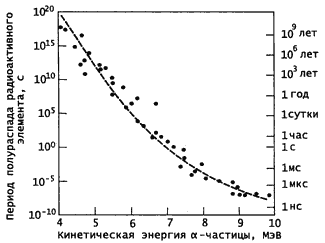 Рис. 2.1. Зависимость периода полураспада радиоактивного элемента от кинетической энергии α-частицы естественно радиоактивного элемента. Штриховая линия – закон Гейгера-Нэттола. Для четно-четных изотопов зависимость периода полураспада от энергии α-распада Qα описывается эмпирическим законом Гейгера-Неттола lg T1/2 = A + B/√Qα, (2.2) где A и B – константы, слабо зависящие от Z. С учётом заряда ядра Z связь между периодом полураспада T1/2 и энергией α-распада может быть представлена в виде lg T1/2 = 1.61(ZEα-1/2 – Z2/3) + 28.9, (2.3) где Z − заряд конечного ядра, период полураспада T1/2 выражен в секундах, а энергия α-частицы Eα − в МэВ. На рис. 2.1 показаны экспериментальные значения периодов полураспада для α-радиоактивных четно-четных изотопов (Z изменяется от 74 до 106) и их описание с помощью соотношения (2.3). Для нечетно-четных, четно-нечетных и нечетно-нечетных ядер общая тенденция зависимости lg T1/2 от Qα сохраняется, но периоды полураспада в 2–100 раз больше, чем для четно-четных ядер с теми же Z и Qα. Для того чтобы происходил α-распад, необходимо, чтобы масса исходного ядра M(A,Z) была больше суммы масс конечного ядра M(A-4, Z-2) и α-частицы Mα: M(A,Z) > M(A-4, Z-2) + Mα. (2.4) В результате α-распада ядра (A,Z) в конечном состоянии образуются два продукта распада: α-частица и ядро (A-4, Z-2). Поэтому энергия α частицы Eα имеет фиксированное значение, определяемое законами сохранения энергии и импульса  (2.5)где Qα = [M(A,Z) – M(A-4, Z-2) + Mα]c2 − энергия α-распада. Так как Mα << M(A-4, Z-2), основная часть энергии α-распада уносится α частицей и лишь ≈ 2% − конечным ядром (A-4, Z-2). Энергетические спектры α-частиц многих радиоактивных элементов состоят из нескольких линий (тонкая структура α-спектров). Причина появления тонкой структуры α-спектра − распад начального ядра (A,Z) на возбужденное состояние ядра (A-4, Z-2). Измеряя спектры α-частиц можно получить информацию о природе возбужденных состояний ядра (A-4, Z-2).
Пробег альфа-частиц, испускаемых радиоактивными веществами, достигает 9 - 8 см в воздухе, а в мягкой биологической ткани - нескольких десятков микрон. Обладая сравнительно большой массой, альфа-частица быстро теряет свою энергию при взаимодействии с веществом, что обусловливает низкую проникающую способность и высокую удельную ионизацию. Пробег альфа-частиц в различных твердых материалах составляет от нескольких микрон до нескольких десятков микрон. Так, например, альфа-частица с энергией 5 4 Мэв имеет пробег 25 мкм в целлофане, 22 мкм в алюминии, 17 мкм в слюде, 9 3 мкм в тантале и 8 4 мкм в золоте. Из этих данных видно, что для пропускания - частиц должна применяться фольга толщиной лишь в несколько микрон.
Пробеги отдельных частиц распределены около среднего пробега по закону Гаусса 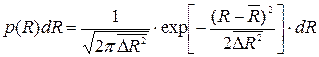 ,где  - средний пробег,  - среднеквадратичное отклонение от среднего значения Относительный разброс пробегов  называется стрэгглингом. Наличие этого разброса приводит к тому, что кривая поглощения имеет не резкий, а плавный спад, такой, как изображен на рис. (для α-частиц).
Принцип работы счетчиков Гейгера основан на эффекте ударной ионизации газовой среды под действием радиоактивных частиц или квантов электромагнитных колебаний в межэлектродном пространстве при высоком ускоряющем напряжении. Устройство состоит из герметичного металлического или стеклянного баллона, наполненного инертным газом (неон, аргон) или газовой смесью. Внутри баллона имеются электроды – катод и анод. Для облегчения возникновения электрического разряда в газовом баллоне создается пониженное давление. Электроды подключаются к источнику высокого напряжения постоянного тока через нагрузочный резистор, на котором формируются электрические импульсы при регистрации радиоактивных частиц. 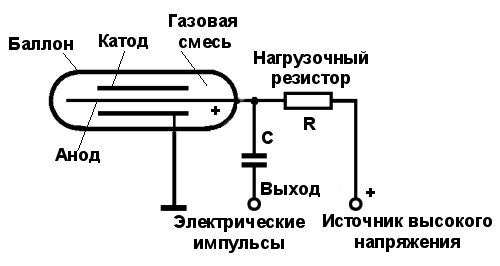 В исходном состоянии газовый промежуток между электродами имеет высокое сопротивление и тока в цепи нет. Когда заряженная частица, имеющая высокую энергию, сталкивается с элементами конструкции датчика (корпус, баллон, катод), она выбивает некоторое количество электронов, которые оказываются в промежутке между электродами. Под действием ускоряющего напряжения в несколько сотен вольт электроны, находящиеся в инертном газе, начинают устремляться к аноду. На этом пути они легко ионизируют молекулы газа, выбивая вторичные электроны. Процесс многократно повторяется и количество электронов лавинообразно увеличивается, что приводит к возникновению разряда между катодом и анодом. В состоянии разряда газовый промежуток в межэлектродном пространстве становится токопроводящим, что обуславливает скачок тока в нагрузочном резисторе. В несамогасящихся счетчиках прекращение разряда достигается отключением источника питания, что приводит счетчик Гейгера в исходное состояние. В самогасящихся галогенных счетчиках, широко применяемых в настоящее время, это достигается за счет введения в газовую среду специальных добавок (хлор, бром, йод, спирт), которые способствуют быстрому прекращению разряда. Также в качестве нагрузочного резистора используют высокоомное сопротивление – несколько единиц или десятков мегаом. Это позволяет за счет падения напряжения на резисторе (во время разряда) резко уменьшить разность потенциалов на электродах счетчика. Как правило, напряжение менее 300 вольт делает невозможным поддержание разряда, и он автоматически прекращается. |
