1-60 мкэ. Геометрическая сторона задач расчета конструкций чрезвычайно разнообразна. Инженерная конструкция может представлять собой
 Скачать 0.85 Mb. Скачать 0.85 Mb.
|
|
1. Классификация и виды конечных элементов Геометрическая сторона задач расчета конструкций чрезвычайно разнообразна. Инженерная конструкция может представлять собой: • стержневую систему (ферму, балку или раму), • двумерный объект (пластину, плиту или оболочку), • объемный или трехмерный объект, • являться комбинацией стержней, пластин, оболочек и т.д. Для геометрического моделирования перечисленных видов инженерных конструкций разработано большое количество разнообразных конечных элементов. Их количество столь велико, что они с трудом поддаются классификации. Грубую классификацию можно осуществить с помощью четырех признаков: • размерность пространства, • количество узловых точек, • количество степеней свободы (возможных перемещений) в узле, • форма конечного элемента. Перечислим наиболее часто используемые разновидности конечных элементов в зависимости от описываемой области. Это стержневые, плоские и, наконец, объемные конечные элементы. 2. Плоские конечные элементы. Степень свободы и расчетная схема. 3. Пространственные конечные элементы. Степень свободы и расчетная схема. 4. Узловые перемещения и усилия в плоском ферменном элементе.  5. Узловые перемещения и усилия в плоском изгибаемом стержне.  6. Местная и глобальная система координат. МКЭ используют общую (глобальную) и местную (локальную) системы координат. Общая система координат принимается для всей расчетной схемы, состоящей из совокупности конечных элементов. Кроме этого, каждый конечный элемент располагается в собственной, местной (локальной) системе координат, строго ориентированной относительно конечного элемента [2]. Матрица жесткости конечных элементов выводится при использовании местной системы координат. Такой подход позволяет получить для всех однотипных элементов матрицы жесткости одного вида и создать библиотеку таких матриц для конечных элементов различных типов. 7. Основные идеи МКЭ. Основная идея МКЭ состоит в том, что: 1) любую непрерывную величину (например, температуру, давление, перемещение) можно аппроксимировать дискретной моделью, которая строится на множестве кусочно-непрерывных функций, определённых на конечном числе подобластей (элементов); 2) кусочно-непрерывные функции определяются с помощью значений непрерывной величины в конечном числе точек рассматриваемой области. 8. Идеализация исходной конструкции. Узлы, элементы, нагрузки. 9. Вектор усилия в узле 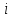 элемента элемента 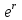 в местной системе осей координат. в местной системе осей координат.Вектор внешних нагрузок в общем виде равен: 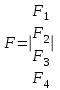 . .10 Вектор перемещений узла 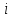 элемента элемента 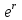 в местной системе осей координат. в местной системе осей координат.Вектор перемещений примет вид 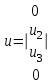 . .11. Матрица жесткости ферменного элемента. 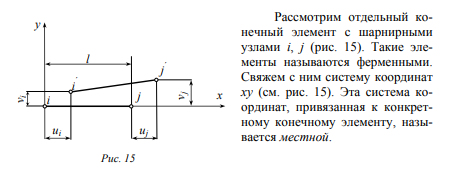   12. Матрица жесткости стержневого плоского конечного элемента.  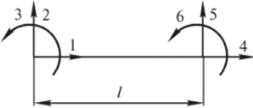 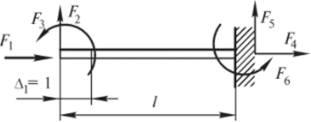 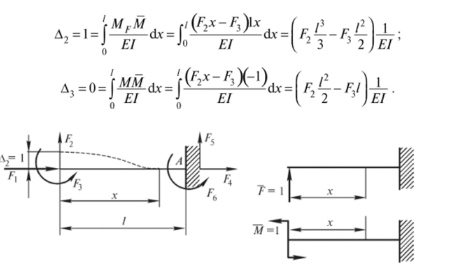 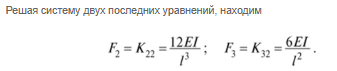 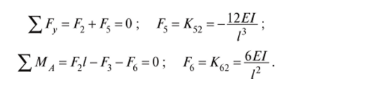 13. Матрица жесткости системы. Матрица жесткости системы 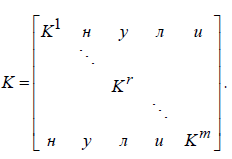 14. Основные уравнения МКЭ. Основные уравнения метода конечных элементов: Уравнение узловых усилий в матричной форме в глобальной системе координат: 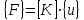 Уравнение узловых усилий в матричной форме в местной системе координат: 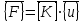 Уравнение перехода вектора узловых усилий из глобальной системы координат в местную: 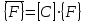 Уравнение перехода вектора узловых перемещений из глобальной системы координат в местную: 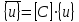 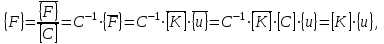 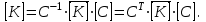 15. Вывод матрицы жесткости изгибаемого элемента. 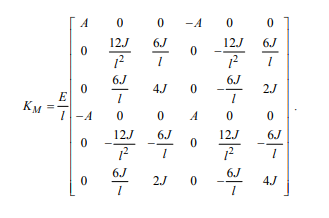 15. Вывод матрицы жесткости изгибаемого элемента. Характеристики совокупности элементов. Матрица жесткости совокупного элемента Порядок расчета ферм по методу конечных элементов. Для заданной фермы необходимо определить: перемещения узлов; реакции опор; напряжения в стержнях. Матрица направляющих косинусов. Для перевода реакций из местной системы координат в общую систему координат Обобщенная матрица жесткости. Составление векторов усилий и перемещений в фермах. При воздействии только вертикальной нагрузки ее опорные реакции будут такими же как у вспомогательной балки. Поэтому ЛВ опорных реакций фермы будут аналогичны ЛВ балки. Для построения ЛВ продольных усилий фермы воспользуемся способами вырезания узлов и сквозных сечений. Так как в стержнях ферм возникают только продольные усилия, перемещения в фермах определяются по формуле: 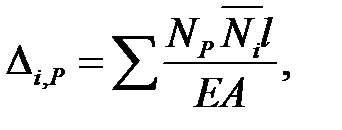 где l - длина стержня; E -модуль упругости; A - площадь поперечного сечения. Матрица жесткости элементов рам. Физический смысл элемента kij матрицы жесткости. это реактивная сила, возникающая в i-ом направлении от заданного единичного перемещения в j-ом направлении Матрица жесткости КЭ в местной системе осей координат 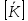 устанавливает связь между единичными перемещениями и усилиями в узловых точках, для горизонтально расположенного элемента Матрица направляющих косинусов [С]. Для перевода реакций из местной системы координат в общую систему координат Перевод матрицы жесткости стержня из местной системы координат в общую систему. матрица направляющих косинусов [С] Условия для формирования вектора узловых нагрузок {F}. необходимо чтобы вся нагрузка была приложена к узлам конструкции Условия и предпосылки точности результатов расчета по МКЭ при расчете стержневой системы (пластины, оболочки, массивного тела). чем меньше линейный размер КЭ, тем больше время вычислений, а ошибки анализа уменьшаются Одномерные, двумерные, трехмерные (массивы) конструкции. Определения и примеры. С понятием "массив" приходится сталкиваться при решении научно-технических и экономических задач обработки совокупностей большого количества значений. В общем случае массив - это структурированный тип данных, состоящий из фиксированного числа элементов, имеющих один и тот же тип. Физический смысл матрицы жесткости К. матрицей жесткости конечного элемента. Физический смысл элемента kij этой матрицы – это реакция (реактивная сила), возникающая в i-ом направлении отзаданного единичного перемещения в j-ом направлении. Вывод матрицы жесткости изгибаемого элемента. Характеристики совокупности элементов. Матрица жесткости совокупного элемента Порядок расчета ферм по методу конечных элементов. Для заданной фермы необходимо определить: перемещения узлов; реакции опор; напряжения в стержнях. Матрица направляющих косинусов. Для перевода реакций из местной системы координат в общую систему координат Обобщенная матрица жесткости. Составление векторов усилий и перемещений в фермах. При воздействии только вертикальной нагрузки ее опорные реакции будут такими же как у вспомогательной балки. Поэтому ЛВ опорных реакций фермы будут аналогичны ЛВ балки. Для построения ЛВ продольных усилий фермы воспользуемся способами вырезания узлов и сквозных сечений. Так как в стержнях ферм возникают только продольные усилия, перемещения в фермах определяются по формуле: 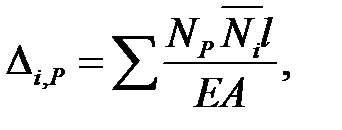 где l - длина стержня; E -модуль упругости; A - площадь поперечного сечения. Матрица жесткости элементов рам. Физический смысл элемента kij матрицы жесткости. это реактивная сила, возникающая в i-ом направлении от заданного единичного перемещения в j-ом направлении Матрица жесткости КЭ в местной системе осей координат 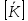 устанавливает связь между единичными перемещениями и усилиями в узловых точках, для горизонтально расположенного элемента Матрица направляющих косинусов [С]. Для перевода реакций из местной системы координат в общую систему координат Перевод матрицы жесткости стержня из местной системы координат в общую систему. матрица направляющих косинусов [С] Условия для формирования вектора узловых нагрузок {F}. необходимо чтобы вся нагрузка была приложена к узлам конструкции Условия и предпосылки точности результатов расчета по МКЭ при расчете стержневой системы (пластины, оболочки, массивного тела). чем меньше линейный размер КЭ, тем больше время вычислений, а ошибки анализа уменьшаются Одномерные, двумерные, трехмерные (массивы) конструкции. Определения и примеры. С понятием "массив" приходится сталкиваться при решении научно-технических и экономических задач обработки совокупностей большого количества значений. В общем случае массив - это структурированный тип данных, состоящий из фиксированного числа элементов, имеющих один и тот же тип. Физический смысл матрицы жесткости К. матрицей жесткости конечного элемента. Физический смысл элемента kij этой матрицы – это реакция (реактивная сила), возникающая в i-ом направлении отзаданного единичного перемещения в j-ом направлении. Физический смысл матрицы жесткости К. Физический смысл элементов 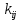 матрицы жесткости матрицы жесткости 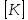 – это реакция по направлению i от единичного перемещения в направлении j – это реакция по направлению i от единичного перемещения в направлении jЭтапы решения задач по методу конечных элементов. Порядок основных этапов расчета по МКЭ: 1)создание чертежа конструкции и нагрузок; 2) создание модели для МКЭ; 3) разбиение модели на сетку КЭ; 4) граничные условия; 5) численное решение СЛАУ; 6) анализ результатов Характеристики совокупности элементов. Метод конечных элементов – это метод расчета, который рассматривает сооружения как совокупность типовых элементов, называемых конечными элементами (КЭ) Наиболее важные этапы в конечно-элементном анализе. Одним из наиболее важных этапов в конечно-элементном анализе является - разделение всей модели на конечные элементы, связанные между собой в узлах Граничные условия. Пример.   Основное уравнение (система уравнений) МКЭ для решения задач при статических нагрузках. Понятия о методе конечных элементов. метод расчета, который рассматривает сооружения как совокупность типовых элементов, называемых конечными элементами (КЭ) Величина жесткости при изгибе, растяжении, кручении. Как обозначается жесткость на изгиб? 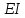 жесткость на растяжение - сжатие? 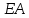 жесткость при сдвиге? 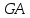 жесткость поперечного сечения при изгибе? 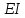 жесткость поперечного сечения при растяжении-сжатии? 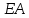 Ферменные и стержневые конечные элементы. Схемы, отличия. 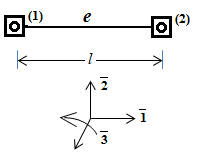 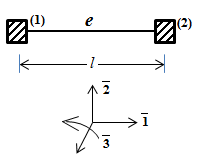 ферменный плоский стержневой конечный элемент Виды КЭ при расчете пространственных сооружений. 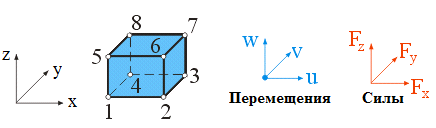 , ,призменный КЭ 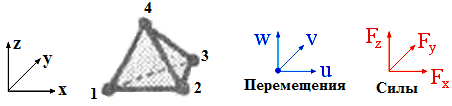 тетраэдальный КЭ Степени свободы в плоских и пространственных узлах. Максимальное число граничных условий, приложенных в узле, равно числу его степеней свободы (3 силы или 3 перемещения) В плоской системе расс-мый узел имеет сколько степени свободы? три степени свободы 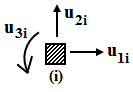 В плоской системе... две степени свободы 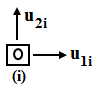 в пространственной системе... шесть степеней свободы 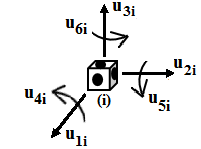 в пространственной системе... три степени свободы 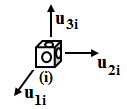 Предпроцессор, процессор, постпроцессор. Препроцессор – предназначен для подготовки и ввода исходных данных в компьютер (разбиение на КЭ и т.д.) Процессор – это блок для математического расчета МКЭ Постпроцессор –предназначен для обработки результатов расчета (анализ) Усилия и деформации, возникающие в стержневом элементе. Какие деформации возникают в стержнях плоской фермы при узловой нагрузке: Растяжение – сжатие Понятия реального объекта, расчетной схемы. Реальный объект, освобожденный от несущественных особенностей, носит название расчетная схема Перемещение и деформация. Определение, различия. Перемещение узла определяется: его поступательными перемещениями вдоль глобальных осей координат X, У и Z и его вращениями относительно этих осей Что называется деформацией тела: Изменения взаимного расположения частиц тела, как правило, вызывающее изменение его размеров и формы Понятия статически определимых и статически неопределимых систем. Примеры. Системы, в которых реакции связей и внутренние усилия можно определить с помощью уравнений равновесия, называются статически определимыми Системы, в которых реакции связей и внутренние усилия нельзя определить с помощью одних лишь уравнений равновесия, называются статически неопределимыми Статическая система называется статически определимой, если число неизвестных сил (внешних опорных реакций или внутренних усилий) соответствует числу уравнений статики. Количество степеней свободы такой системы равно нулю. Величины опорных реакций и внутренних усилий по принципу механического равновесия можно определить из величин внешних нагрузок. Все другие системы называются статически неопределимыми. Статически неопределимыми системами называются стержневые системы, для определения реакций опор в которых только уравнений равновесия недостаточно. Число связей, наложенных на статически неопределимую систему, больше того количества связей, которые обеспечивают геометрическую неизменяемость конструкции. Определяем степень свободы системы по формуле Чернышевой: W=3D-2Ш-C0  Ферма — стержневая система остающаяся геометрически неизменяемой после замены её жёстких узлов шарнирными. В элементах фермы, при отсутствии расцентровки стержней и внеузловой нагрузки, возникают только усилия и деформации растяжения-сжатия.  при расчете сооружения могут быть реализованы различные варианты МКЭ в формах метода сил, метода перемещений и смешанного метода. В настоящее время широкое распространение получил МКЭ в форме метода перемещений. Матрица преобразования – матрица, с помощью которой можно от одной системы координат перейти к другой. Матрица преобразований предназначена для вычисления новых координат элемента с целью его трансформации и позволяет установить множество преобразований одновременно. Различают двумерную и трёхмерную матрицу, они отличаются друг от друга размером и пространством, на которое ориентированы. Модель дискретная – описывает состояние системы с конеч-ным числом степеней свободы. Модель континуальная –описывает состояние системы с бес-конечно большим числом степеней свободы. Как известно, каждый столбец матрицы жесткости элемента представляет собой усилия, действующие на элемент в узлах при единичном смещении по направлению какой-либо степени свободы. Поэтому, для построения любого столбца матрицы жесткости элемента следует задать единичное смещение по направлению соответствующей степени свободы элемента и найти усилия, действующие при этом на его узлы. Выполнив последовательно эту операцию для всех степеней свободы элемента, по столбцам построим всю матрицу жесткости элемента. 52. Расчет стержневых систем. Постановка задачи. Решение с помощью МКЭ получают, выполняя следующие шаги: 1. Определяют задачу и нагрузки, создают эскиз конструкции. 2. Строят геометрическую модель конструкции с помощью модулей твердотельного моделирования, встроенных в КЭ программы, или системы автоматизированного проектирования. 3. Создают КЭ сетку. 4. Задают граничные условия (кинематические связи и нагрузки). 5. Решают систему уравнений МКЭ. 6. Анализируют полученные результаты. 53.   55. Матрица жесткости в глобальной системе координат – квазидиагональная матрица, элементами которой являются жесткости отдельных элементов системы, записанные в единой (глобальной) системе координат. 56. Матрица направляющих косинусов Матрицей поворота (или матрицей направляющих косинусов) называется матрица, умножение любого вектора на которую не меняет его длины.  57. Преобразование матрицы жесткости балочного элемента при переходе к глобальной системе координат Рассмотрим балочный элемент в глобальной системе координат (рис. 14). 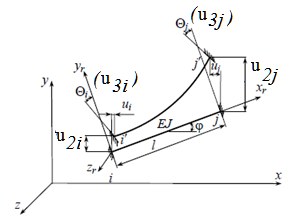 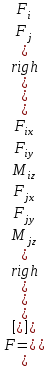 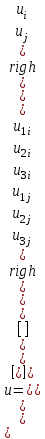 Подобно тому, как выше была получена матрица жесткости ферменного элемента в глобальной системе координат , может быть получена матрица жесткости балочного элемента в глобальной системе координат: F= K u где матрица К имеет вид: 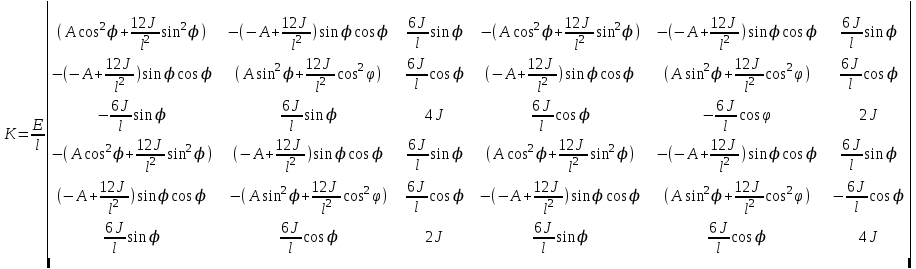 58. В расчетной модели сооружения по МКЭ нагрузка должна быть приложена только в узлах. Поэтому действующую на систему внеузловую нагрузку необходимо переносить в узлы. Порядок переноса нагрузки в узлы расчетной модели в простых случаях остается таким же как и ранее. Например, в стержневых системах используется таблица метода перемещений. 59-60.  Метод конечных элементов – это метод расчета сооружений, основанный на рассмотрении сооружения как совокупности типовых элементов, называемых конечными элементами (КЭ). МКЭ – дискретный метод. В методе конечных элементов (МКЭ) сложная конструкция разделяется на небольшие элементы (конечные элементы, КЭ). Любая непрерывная величина (перемещения, напряжения, температура и т.п.) аппроксимируется в пределах каждого элемента. Результатом моделирования является получение распределения искомой величины во всей конструкции. В этом методе сооружение делится на определенное число КЭ, соединяемых между собой в узлах конечно-элементной модели. А нагрузка, действующая на сооружение, переносится в узлы. Это позволяет определять НДС сооружения через узловые усилия и перемещения конечно-элементной модели. |
