Ярмухаметова Э.В._Полный отчет_МАТ-2231z. Геометрические вероятности. Имитационное компьютерное моделирование вероятностных опытов
 Скачать 195.38 Kb. Скачать 195.38 Kb.
|
|
ОТЧЕТ По лабораторной работе по математике (ЛРМ 1, Вариант 1) Ф.И.О.: Ярмухаметова Э.В.______________, гр. _2231з_______ Дата: 21.03.2023 Тема: «Геометрические вероятности. Имитационное компьютерное моделирование вероятностных опытов». Цель. Овладеть практическими навыками и закрепить теоретический материал по вычислению вероятностей по геометрическому способу. Решить задачу: «На окружности случайным образом поставлены три точки A, B, C. Вариант I. Какова вероятность того, что ΔABC остроугольный?» Теория. Предполагается, что вероятность попадания «случайно брошенной» точки в произвольное подмножество F пропорционально мере этого подмножества и не зависит ни от его расположения, ни от его формы. Геометрическая вероятность сохраняет свойства вероятности событий, введенных для классического определения вероятностей, но расширяет возможности определения вероятности, когда имеется бесконечное число равнозначных исходов. Определение. Геометрической вероятностью P(F) события F называется отношение меры μ (по Лебегу) множества F, благоприятствующего событию F, к мере вероятностного пространства Ω всех возможных равновероятных исходов: P(F) = 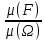 . .Понятие мера множества систематически изучается в курсе «Теория функций действительного переменного» [4]. Укажем кратко наиболее употребимые меры:
Таким образом, для решения задачи мы должны ввести вероятностное пространство 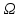 , знать его меру Лебега , знать его меру Лебега 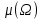 , указать множество F, благоприятствующее событию F, вычислить его меру , указать множество F, благоприятствующее событию F, вычислить его меру 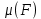 и, соответственно, вычислить вероятность P(F). и, соответственно, вычислить вероятность P(F).Ход работы: По условию событие F – «Получился остроугольный треугольник». Необходимо выполнить несколько шагов: 1° Так как достаточно поставить на окружности 2 случайные точки, зафиксировав третью, то размерность вероятностного пространства Ω равна 2. Введем 2 непрерывных случайных величины: 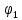 – круговая координата первой точки, – круговая координата первой точки, 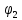 – круговая координата второй точки. – круговая координата второй точки.2° Определяем диапазон изменения 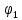 и и 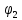 и соответствующую меру μ(Ω) пространства Ω всех возможных равновероятных исходов. Можно принять (в градусах): 0 ≤ и соответствующую меру μ(Ω) пространства Ω всех возможных равновероятных исходов. Можно принять (в градусах): 0 ≤ 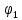 ≤ 360 и 0 ≤ ≤ 360 и 0 ≤ 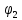 ≤ 360. Пространство Ω есть квадрат 360×360 град2 на плоскости Oxy; его мера (площадь) равна μ(Ω) = 3602. ≤ 360. Пространство Ω есть квадрат 360×360 град2 на плоскости Oxy; его мера (площадь) равна μ(Ω) = 3602. 3° Определим благоприятствующий диапазон изменения 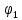 и и 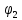 и соответствующую меру μ(F) множества F исходов, благоприятствующих событию F путем решения неравенств на плоскости Oxy в пределах Ω. Для этого необходимо вычислить углы получившегося треугольника. и соответствующую меру μ(F) множества F исходов, благоприятствующих событию F путем решения неравенств на плоскости Oxy в пределах Ω. Для этого необходимо вычислить углы получившегося треугольника.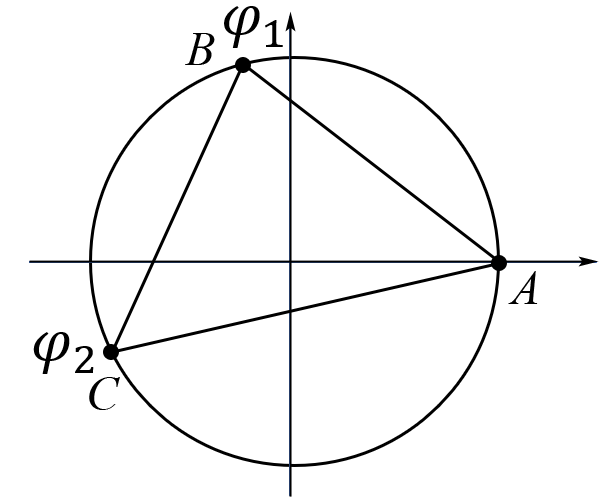 Тогда 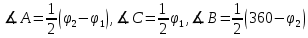 Условие остроугольности треугольника АВС: 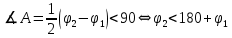 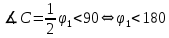 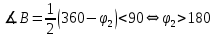 Учтем еще условие 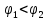 что соответствует верхней левой половине квадрата. В квадрате 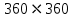 это соответствует заштрихованной области: это соответствует заштрихованной области: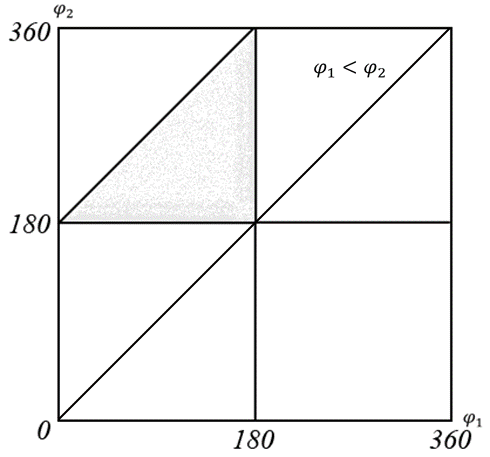 По площади заштрихованная область составляет 1/8 часть всего квадрата. Значит, искомая вероятность равна 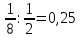 . .Проведем имитационное компьютерное моделирование вероятностных опытов. Для этого потребуется следующее. 1°. С помощью генератора случайных чисел генерируем два случайных числа 0 ≤ x ≤ 360 и 0 ≤ y ≤ 360 (градусы). Это можно сделать с помощью функции rnd()*360 языка VBA (встроен в MS Excel). 2°. Напишем программу, которая на основе этих чисел вычисляет углы получившегося треугольника и проверяет условия остроугольности. В случае успеха счетчик успехов 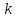 увеличиваем на единицу. увеличиваем на единицу.Программу на языке Visual Basic for Applications (разновидность VB, встроенная в MS Excel), осуществляющей моделирование, приведем ниже. Sub Лаб_1() ' Лаб_1 Макрос Dim i, n, k As Long Dim ii As Integer Dim x, r, fi1, fi2 As Double r = 360 ' Ввод числа экспериментов n = Cells(2, "A") Randomize k = 0 For i = 1 To n ' Генерация двух дуг на окружности fi1 = Rnd() * r fi2 = Rnd() * r x = fi2 If fi2 < fi1 Then fi2 = fi1 fi1 = x End If ' Вычисление углов a = (fi2 - fi1) / 2 c = fi1 / 2 b = (r - fi2) / 2 ' Проверка условий остроугольности If a < 90 And b < 90 And c < 90 Then k = k + 1 Next i ii = 2 Do While Cells(ii, "C") <> "" ii = ii + 1 Loop ' Вывод результатов эксперимента Cells(ii, "C") = n Cells(ii, "D") = k Cells(ii, "E") = k / n End Sub 3°. Находим относительную частоту события F – «Треугольник остроугольный» по формуле w(F) = 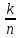 . Меняя число n имитационных опытов, будем получать соответствующие частоты событий . Меняя число n имитационных опытов, будем получать соответствующие частоты событий 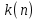 и соответствующие относительные частоты w = и соответствующие относительные частоты w = 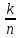 . .5°. Результаты каждого имитационного опыта заносим в итоговую отчетную таблицу и строим ломаную линию относительных частот в сопоставлении с теоретической вероятностью события F. Результаты и обсуждение. Результаты имитационного моделирования задачи о гипотезе «Треугольник - остроугольный» для треугольника, вписанного в окружность, приведем в следующей таблице:
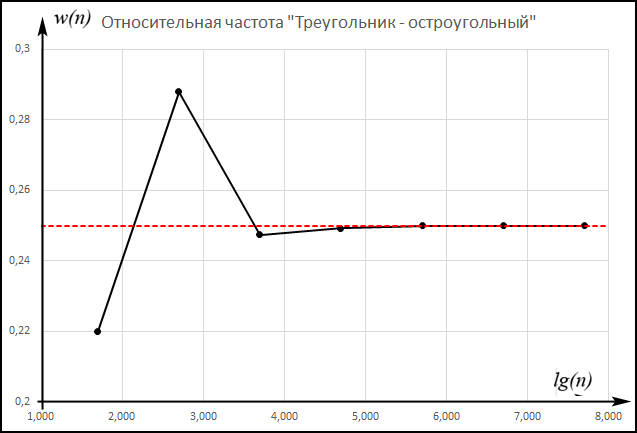 Выводы. Для заданного случайного события вычислена теоретическая вероятность, используя геометрическое определение вероятности на плоскости. Написана программа имитационного моделирования, которая при большом числе испытаний (формально при n → ∞) подтвердила, что относительные частоты стремятся к теоретической вероятности события F, равной 0,25. Список цитированной литературы. [1] Гмурман В.Е. Теория вероятностей и математическая статистика. Учебное пособие для вузов. – М.: Высшая школа [издания разные лет]. [2] Колмогоров А.Н. Основные понятия теории вероятностей. М.: Наука, 1974. – 124 с. URL: https://b-ok.cc/dl/2339066/a9821b [3] Письменный Д.Т. Конспект лекций по теории вероятностей и математической статистике. М.: Айрис-Пресс, 2004. – 256 с. [4] Колмогоров А.Н., Фомин С.В. Элементы теории функций и функционального анализа. М.: Наука, 2004. – 572 с. URL: https://studizba.com/files/show/pdf/40466-3-a-n-kolmogorov-s-v-fomin--elementy.html ОТЧЕТ По лабораторной работе по математике (ЛРМ 2) Ф.И.О.: Ярмухаметова Э.В., гр. МАТ-2231z Дата: 21.03.2023 Тема: «Геометрические вероятности. Имитационное компьютерное моделирование вероятностных опытов». Цель. Овладеть практическими навыками и закрепить теоретический материал по вычислению вероятностей по геометрическому способу. Решить задачу: «От трех палочек одинаковой длины случайным образом отломили по одному кусочку. Какова вероятность того, что из них удастся составить треугольник?» Теория. Предполагается, что вероятность попадания «случайно брошенной» точки в произвольное подмножество F пропорционально мере этого подмножества и не зависит ни от его расположения, ни от его формы. Геометрическая вероятность сохраняет свойства вероятности событий, введенных для классического определения вероятностей, но расширяет возможности определения вероятности, когда имеется бесконечное число равнозначных исходов. Определение. Геометрической вероятностью P(F) события F называется отношение меры μ (по Лебегу) множества F, благоприятствующего событию F, к мере вероятностного пространства Ω всех возможных равновероятных исходов: P(F) = 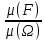 . .Понятие мера множества систематически изучается в курсе «Теория функций действительного переменного» [4]. Укажем кратко наиболее употребимые меры:
Таким образом, для решения задачи мы должны ввести вероятностное пространство 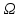 , знать его меру Лебега , знать его меру Лебега 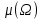 , указать множество F, благоприятствующее событию F, вычислить его меру , указать множество F, благоприятствующее событию F, вычислить его меру 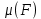 и, соответственно, вычислить вероятность P(F). и, соответственно, вычислить вероятность P(F).Ход работы: По условию событие F – «Удалось составить треугольник». Необходимо выполнить несколько шагов: 1° Так как необходимо иметь 3 отрезка случайной длины, то размерность вероятностного пространства Ω равна 3. Введем 3 непрерывных случайных величины: 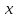 – длина первого кусочка, – длина первого кусочка, 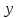 – длина второго кусочка, – длина второго кусочка, 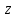 – длина третьего кусочка. – длина третьего кусочка.2° Определяем диапазон изменения 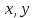 и и 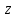 и соответствующую меру μ(Ω) пространства Ω всех возможных равновероятных исходов. Можно принять (в долях): 0 ≤ и соответствующую меру μ(Ω) пространства Ω всех возможных равновероятных исходов. Можно принять (в долях): 0 ≤ 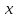 ≤ 1, 0 ≤ ≤ 1, 0 ≤ 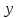 ≤ 1 и 0 ≤ ≤ 1 и 0 ≤ 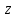 ≤ 1. Пространство Ω есть куб 1×1×1 в пространстве Oxy ≤ 1. Пространство Ω есть куб 1×1×1 в пространстве Oxy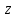 ; его мера (объем) равна μ(Ω) = 1. ; его мера (объем) равна μ(Ω) = 1. 3° Определим благоприятствующий диапазон изменения 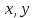 и и 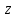 и соответствующую меру μ(F) множества F исходов, благоприятствующих событию F путем решения неравенств в пространстве Oxy и соответствующую меру μ(F) множества F исходов, благоприятствующих событию F путем решения неравенств в пространстве Oxy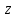 в пределах Ω. Для этого необходимо выполнить «условия треугольника»: в пределах Ω. Для этого необходимо выполнить «условия треугольника»: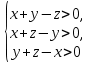 Область куба, где выполняются все три условия, можно представить на рисунке 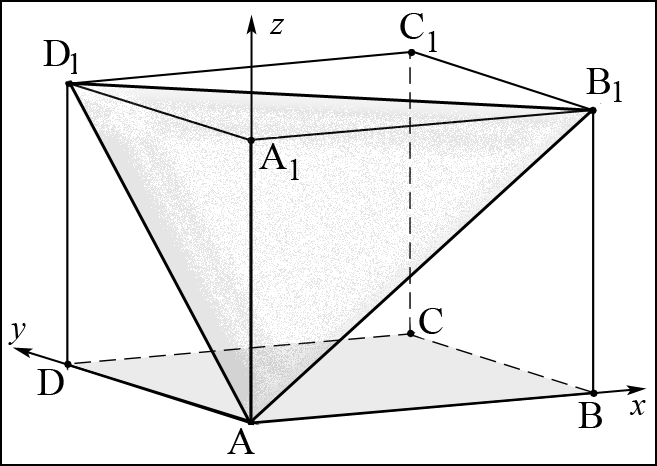 Здесь заштрихованная плоскость соответствует уравнению 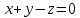 , а области, противоположной первому неравенству, соответствует пирамида с основанием , а области, противоположной первому неравенству, соответствует пирамида с основанием 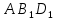 и вершиной и вершиной 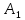 . Можно подсчитать, что ее объем равен . Можно подсчитать, что ее объем равен 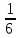 . Аналогично неравенством, противоположным второму, отрезается область с вершиной . Аналогично неравенством, противоположным второму, отрезается область с вершиной 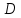 тоже объемом тоже объемом 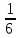 . Неравенством, противоположным третьему, отрезается область с вершиной . Неравенством, противоположным третьему, отрезается область с вершиной 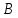 тоже объемом тоже объемом 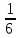 . Таким образом, отрезается объем, равный . Таким образом, отрезается объем, равный 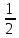 , а значит оставшийся объем равен , а значит оставшийся объем равен 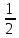 и все точки этой области удовлетворяют всем трем «неравенствам треугольника». и все точки этой области удовлетворяют всем трем «неравенствам треугольника».Значит, искомая вероятность равна 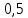 . .Проведем имитационное компьютерное моделирование вероятностных опытов. Для этого потребуется следующее. 1°. С помощью генератора случайных чисел генерируем три случайных числа 0 ≤ x ≤ 1, 0 ≤ y ≤ 1 и 0 ≤ y ≤ 1. Это можно сделать с помощью функции rnd() языка VBA (встроен в MS Excel). 2°. Напишем программу, которая на основе этих чисел проверяет выполнение трех «неравенств треугольника». В случае успеха счетчик успехов 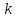 увеличиваем на единицу. увеличиваем на единицу.Программу на языке Visual Basic for Applications (разновидность VB, встроенная в MS Excel), осуществляющей моделирование, приведем ниже. Sub Лаб_2() ' Лаб_2 Макрос Dim i, n, k As Long Dim ii As Integer Dim l1, l2, l3 As Double ' Ввод числа экспериментов n = Cells(2, "A") Randomize k = 0 ' Генерация трех сторон треугольника For i = 1 To n l1 = Rnd() l2 = Rnd() l3 = Rnd() ' Проверка условий существования треугольника If l1 < l2 + l3 And l2 < l1 + l3 And l3 < l1 + l2 Then k = k + 1 Next i ii = 2 Do While Cells(ii, "C") <> "" ii = ii + 1 Loop ' Вывод результатов эксперимента Cells(ii, "C") = n Cells(ii, "D") = k Cells(ii, "E") = k / n End Sub 3°. Находим относительную частоту события F – «Треугольник существует» по формуле w(F) = 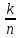 . Меняя число n имитационных опытов, будем получать соответствующие частоты событий . Меняя число n имитационных опытов, будем получать соответствующие частоты событий 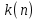 и соответствующие относительные частоты w = и соответствующие относительные частоты w = 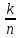 . .Результаты и обсуждение. Результаты каждого имитационного опыта заносим в итоговую отчетную таблицу и строим ломаную линию относительных частот в сопоставлении с теоретической вероятностью события F. Результаты имитационного моделирования задачи о существовании треугольника:
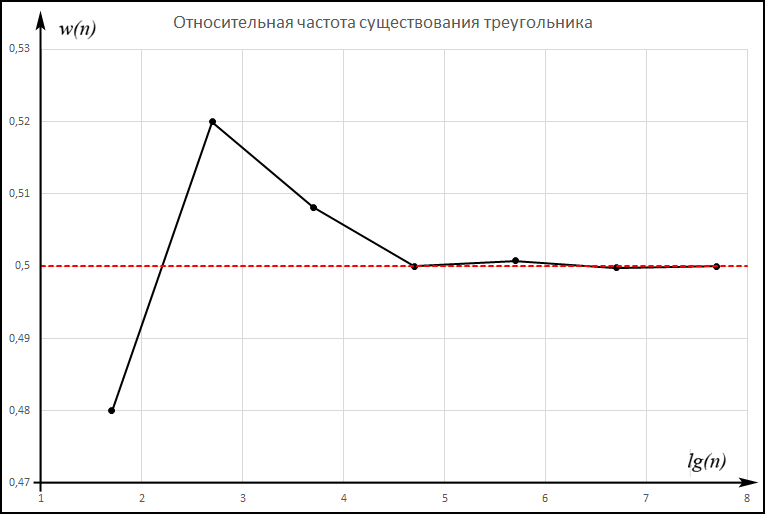 Выводы. Для заданного случайного события вычислена теоретическая вероятность, используя геометрическое определение вероятности в пространстве. Написана программа имитационного моделирования, которая при большом числе испытаний (формально при n → ∞) подтвердила, что относительные частоты стремятся к теоретической вероятности события F, равной 0,5. Список цитированной литературы. [1] Гмурман В.Е. Теория вероятностей и математическая статистика. Учебное пособие для вузов. – М.: Высшая школа [издания разные лет]. [2] Колмогоров А.Н. Основные понятия теории вероятностей. М.: Наука, 1974. – 124 с. URL: https://b-ok.cc/dl/2339066/a9821b [3] Письменный Д.Т. Конспект лекций по теории вероятностей и математической статистике. М.: Айрис-Пресс, 2004. – 256 с. [4] Колмогоров А.Н., Фомин С.В. Элементы теории функций и функционального анализа. М.: Наука, 2004. – 572 с. URL: https://studizba.com/files/show/pdf/40466-3-a-n-kolmogorov-s-v-fomin--elementy.html 3° Самостоятельное решение упражнений с оформлением в виде файла MS Word В а р и а н т I. З а д а ч а I.1°. Весной катер идёт против течения реки в 2⅔ раза медленнее, чем по течению. Летом течение становится на 1 км/ч медленнее. Поэтому летом катер идёт против течения в 1½ раза медленнее, чем по течению. Найдите скорость течения весной (в км/ч). Решение. Введем неизвестные: 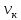 – собственная скорость катера (в неподвижной воде), – собственная скорость катера (в неподвижной воде), 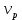 – скорость течения реки весной. Тогда уравнение для весны: – скорость течения реки весной. Тогда уравнение для весны: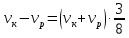 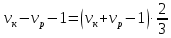 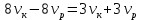 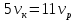 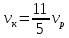 Уравнение для лета: 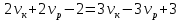 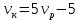 Приравниваем скорости катера: 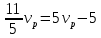 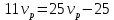 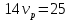 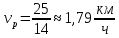 Ответ: 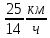 . .З а д а ч а I.2°. Вездеход, находящийся на пересеченной местности в 27 км от прямолинейной шоссейной дороги, должен доставить геологов в населенный пункт, расположенный на шоссе. Расстояние от точки шоссе, ближайшей к вездеходу, до населенного пункта равно 45 км. По пересеченной местности вездеход двигается со скоростью 44 км/ч, а по шоссе – 55 км/ч. На каком расстоянии от населенного пункта вездеход должен выехать на шоссе, чтобы время движения было наименьшим? Решение. Рассмотрим схему движения вездехода: 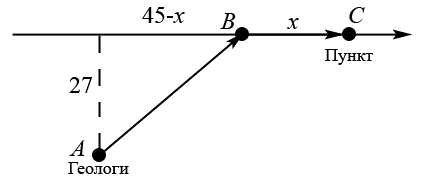 Введем неизвестное 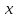 - расстояние BC от точки выхода вездехода на шоссе до населенного пункта. Тогда дорога по пересеченной местности равна - расстояние BC от точки выхода вездехода на шоссе до населенного пункта. Тогда дорога по пересеченной местности равна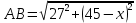 Общее время движения вездехода равно 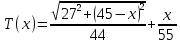 Вычислим производную от этой функции 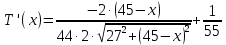 Решим уравнение: 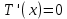 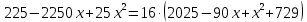 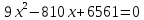 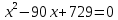 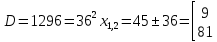 Значение 81 км слишком велико, не подходит под условия задачи. Рассмотрев окрестность точки 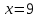 , видим, что производная меняет знак с минуса на плюс, значит найденная точка – минимум функции , видим, что производная меняет знак с минуса на плюс, значит найденная точка – минимум функции 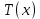 . .Ответ: 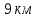 . .З а д а ч а I.3°. Двум дорожно-строительным бригадам поручено строительство шоссейной дороги между пунктами А и В. В течение 40 дней бригады работали отдельно, сначала первая, потом вторая, причем одна из них выполнила 1/3, а другая 1/6 всей работы. На 41 день бригады стали работать совместно и оставшуюся часть дороги построили за 18 дней. Определить, за сколько дней каждая бригада, работая отдельно, могла бы построить шоссе. Решение. Введем неизвестные: 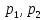 – производительности бригад с размерностью, равной доли всей работы, выполненной в день, – производительности бригад с размерностью, равной доли всей работы, выполненной в день, 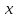 - дн. – работала первая бригада отдельно, - дн. – работала первая бригада отдельно, 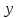 дн. – работала вторая бригада отдельно. Составим уравнения: дн. – работала вторая бригада отдельно. Составим уравнения: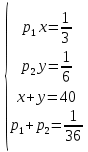 Последнее уравнение вытекает из условия, что две бригады (с производительностью 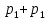 ) выполнили за 18 дней половину всей работы. ) выполнили за 18 дней половину всей работы.Выразим из третьего уравнения 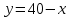 и подставим во второе: и подставим во второе: 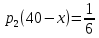 . .Первое уравнение умножим на 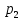 : : 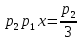 , новое второе умножим на , новое второе умножим на 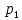 : : 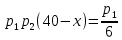 и сложим: и сложим: 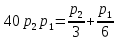 . .Из последнего уравнения выразим 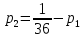 и подставим в предыдущее. и подставим в предыдущее.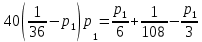 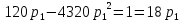 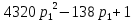 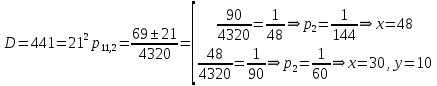 Подходит ответ: 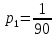 , , 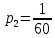 Ответ: первая бригада, работая отдельно, могла бы построить шоссе за 90 дней, вторая бригада, работая отдельно, могла бы построить шоссе за 60 дней. З а д а ч а I.4°. При изготовлении консервной банки цилиндрической формы заданной вместимости V требуется металл двух видов: на боковую поверхность – I сорта, на основания – II сорта, стоимость которого в 2 раза меньше, чем стоимость I сорта. При каком отношении высоты банки к радиусу ее основания затраты на металл будут наименьшими? Решение. Введем 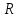 – радиус основания цилиндра, – радиус основания цилиндра, 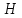 - высота цилиндра. Тогда объем цилиндра равен - высота цилиндра. Тогда объем цилиндра равен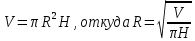 Площадь двух оснований цилиндра равна 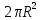 , площадь боковой поверхности цилиндра равна , площадь боковой поверхности цилиндра равна 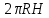 . Пусть . Пусть 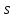 – стоимость одного квадратного метра металла для оснований, тогда – стоимость одного квадратного метра металла для оснований, тогда 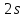 – стоимость металла для боковой поверхности. Общая стоимость металла для всей банки равна – стоимость металла для боковой поверхности. Общая стоимость металла для всей банки равна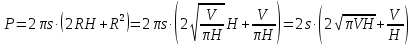 От последнего выражения вычислим производную по 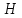 и приравняем ее к нулю: и приравняем ее к нулю: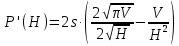 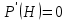 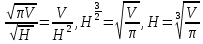 . .Подставим это значение в выражение для 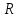 . Получим . Получим 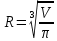 . .Тогда отношение 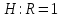 . .Ответ: 1. З а д а ч а I.5°. Иван, Тит и Фома подозреваются в поджоге кооперативной палатки. На допросе они дали следующие показания: Иван: Поджег Тит. Тит: Я не поджигал. Фома: Я не поджигал. Дополнительное расследование показало, что ровно один из них сказал правду. Кто поджег палатку? Решение. Разберем все возможные случаи ответа на вопрос: «Кто поджег палатку?»
Видим, ситуация, когда ровно один сказал правду (истина), реализовалась только, если Фома поджег палатку. Ответ: Фома. | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
