реферат по математике. Геометрическое и гипергеометрическое распределение
 Скачать 189.44 Kb. Скачать 189.44 Kb.
|
|
Министерство сельского хозяйства РФ ФГОУ ВПО « Оренбургский Государственный Аграрный Университет» Институт управления Кафедра организации работы с молодежью Реферат по дисциплине: «Математика» на тему: «Геометрическое и гипергеометрическое распределение» Выполнил: студент группы Проверила: Оренбург - 2010 Содержание Введение Одним из важнейших понятий математической статистики является понятие случайной величины. Под случайной величиной понимается переменная, которая в результате испытания в зависимости от случая принимает одно из возможного множества своих значений (какое именно – заранее неизвестно). Случайная величина называется дискретной, если множество ее значений конечное, или бесконечное, но счетное. Законом распределения случайной величины называется всякое соотношение, устанавливающее связь между возможными значениями случайно величины и соответствующими им вероятностями. Закон распределения дискретной случайной величины дает исчерпывающую информацию о ней, так как позволяет вычислить вероятности любых событий, связанных со случайной величиной. Основными законами распределения дискретных случайных величин являются: биномиальный закон распределения; закон распределения Пуассона; геометрическое распределения; гипергеометрическое распределение. В данной работе рассматривается геометрический закон распределения случайной величины. 1. Описание геометрического закона распределения Дискретная случайная величина Х=m имеет геометрическое распределение, если она принимает значения 1, 2, …, m, … (бесконечное, но счетное множество значений) с вероятностями 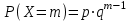 где 0 Ряд геометрического распределения случайной величины имеет вид:
Нетрудно видеть, что вероятности pi образуют геометрическую прогрессию с первым членом p и знаменателем q (отсюда название «геометрическое распределение»). Впервые термин геометрическое распределение был использован в работе Феллера (Feller, 1950). Определение геометрического ряда распределения корректно, так как сумма ряда: 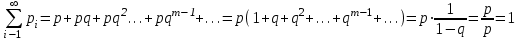 (так как 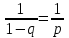 есть сумма геометрического ряда есть сумма геометрического ряда 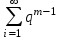 при при 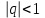 ). ).Случайная величина Х = m, имеющая геометрическое распределение, представляет собой число m испытаний, проведенных по схеме Бернулли, с вероятностью р наступления события в каждом испытании до первого положительного исхода. Так, например, число вызовов радистом корреспондента до тех пор, пока вызов не будет принят, есть случайная величина, имеющая геометрическое распределение, График функции вероятности представлен на рис.1. 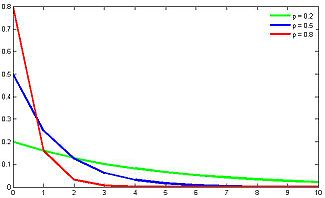 Рис.1. Функция вероятности геометрического распределения случайной величины Описание геометрического закона распределения с помощью функции вероятности не является единственным, а главное не универсально. Для описания закона распределения случайной величины Х возможен и другой подход: рассматривать не вероятности событий Х=х для разных х (как это имеет место в ряде распределения), а вероятности события Х<х, где х – текущая переменная. Вероятности Р(Х<х), очевидно, зависит от х, т.е. является некоторой функцией от х. Функцией распределения случайной величины Х называется функция F(х), выражающая для каждого х вероятность того, что случайная величина Х примет значение, меньшее х: 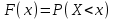 Геометрически функция распределения интерпретируется как вероятность того, что случайная точка Х попадет левее заданной точки х. Функция геометрического распределения имеет вид: 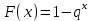 График функции геометрического распределения представлен на рис.2. 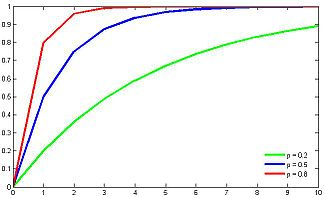 Рис.2. Функция геометрического распределения Основными параметрами геометрического закона распределения являются: число m – число «неудач» до первого «успеха», m = 1,2,3 …; вероятность «успеха» 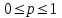 ; ;вероятность «неудачи» q = 1 – p. Основными характеристиками закона распределения является математическое ожидание и дисперсия. Вычислим математическое ожидание и дисперсию геометрического закона распределения с помощью выше перечисленных параметров. Математическим ожиданием, или средним значением, М(Х) дискретной случайной величины Х называется сумма произведений всех ее значений на соответствующие им вероятности: 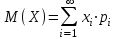 Для геометрического закона распределения получим: 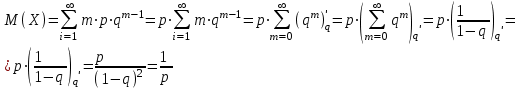 Дисперсией D(Х) случайной величины Х называется математическое ожидание квадрата ее отклонения от математического ожидания: 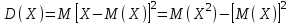 Для геометрического закона распределения получим: 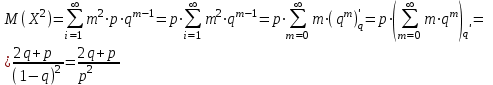 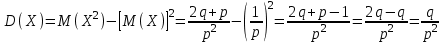 Следует отметить следующие свойства геометрического закона распределения: Из всех дискретных распределений с фиксированным средним μ > 1 геометрическое распределение Geom(1 / μ) является одним из распределений с максимальной информационной энтропией. Если  Геометрическое распределение бесконечно делимо. Если то есть количество прошлых «неудач» не влияет на количество будущих «неудач». Геометрическое распределение — это единственное дискретное распределение со свойством отсутствия памяти. Геометрическое распределение является частным случаем отрицательного биномиального распределения: Если 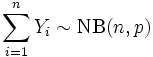 Пример. Пусть игральная кость вбрасывается до выпадания первой «шестёрки». Тогда вероятность, что нам потребуется не больше трёх вбросов равна: Ожидаемое число бросков равно: 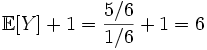 2. Оптимальные оценки параметров закона геометрического распределения и функции этих параметров на основе метода достаточных статистик Геометрический закон распределения задается параметром р (вероятность «успеха»). Известно, что математическое ожидание случайной величины Х, распределенной по геометрическому закону распределения, равно ожидание 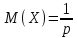 Следовательно, оценка параметра р геометрического закона распределения равна 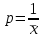 3.Гипергеометрическое распределение. Для вывода функции гипергеометрического распределения проводятся испытания (выборка) по схеме невозвращающегося шара. В этом случае вероятность появления события Е k-раз в n зависимых испытаниях подвергается влиянию не только числа отбираемых единиц n, но и численности всей генеральной совокупности N. Если p доля единиц генеральной совокупности, обладающих изучаемым признаком, а q – доля необладающих этим признаком, то вероятность появления события Е k раз n зависимых испытаний определяется по формуле: 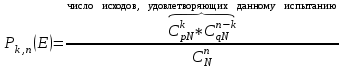 , где , где 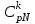 - число сочетаний из pN=M элементов генеральной совокупности, обладающих изучаемым признаком по k; - число сочетаний из pN=M элементов генеральной совокупности, обладающих изучаемым признаком по k; 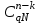 - число сочетаний из qN=N-M единиц, необладающих изучаемым признаком n-k единиц; - число сочетаний из qN=N-M единиц, необладающих изучаемым признаком n-k единиц; 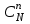 - число исходов, удовлетворяющих и неудовлетворяющих данному испытанию. - число исходов, удовлетворяющих и неудовлетворяющих данному испытанию.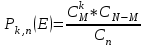 Математическое ожидание гипергеометрического распределения не зависит от объема генеральной совокупности и как в биномиальном распределении определяется по формуле: 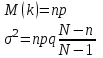 , где , где 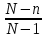 - корректирует дисперсию при бесповторном отборе в зависимости от численности выборки и генеральной совокупности. - корректирует дисперсию при бесповторном отборе в зависимости от численности выборки и генеральной совокупности.Если численность генеральной совокупности достаточно велика, то 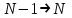 , в этом случае , в этом случае 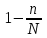 , то , то 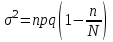 , то есть, зная параметры биномиального распределения всегда можно рассчитать параметры гипергеометрического. , то есть, зная параметры биномиального распределения всегда можно рассчитать параметры гипергеометрического.Выводы Геометрическое распределение описывает время, протекающее до наступления определенного числа неудач. Частным случаем распределения Паскаля является геометрическое распределение, получаемое при с=1. Экспоненциальное распределение для непрерывного случайного аналогично геометрическому для дискретного случая. Если в геометрическом распределении случайная величина представляет число испытаний до первого отказа, то в экспоненциальном в непрерывном случае, соответствующим аналогом будет промежуток до первого отказа. Геометрический закон распределения случайной величины широко используется при решении различных задач. Литература Кремер Н.Ш. Теория вероятностей и математическая статистика: Учебник для вузов. –М.: ЮНИТИ-ДАНА, 2003. Практикум по статистике: Учеб. пособие для вузов./под ред. В.М. Симчеры. – М.: Финстатинформ, 1999. Статистика: учебник / под ред. В.С. Мхитаряна. – М.: Экономистъ, 2005. |
