phpyk Аударғаным. Геометриялы есептерді шыаруа йрету
 Скачать 54.83 Kb. Скачать 54.83 Kb.
|
 Әдістемелік құралда геометриялық есептердің түрлері және олармен жұмыс істеу әдістері сипатталған. Әртүрлі типтегі геометриялық есептерді сәтті шешуге қажетті теориялық материал да берілген. Ақпарат жаңадан бастаған мұғалімдер үшін пайдалы болады. Геометриялық есептерді шығаруға үйрету (тәжірибені қорыту) Кіріспе Математикалық білім беруде есептерді шешу маңызды рөл атқарады. Есептер шығаруға үйрету мәселесін психологиялық зерттеулер геометриялық есептерді шығаруда оқушылардың жалпы біліктері мен дағдыларының қалыптаспауының негізгі себептері оқушыларға есептердің мәні мен оларды шешу жолдары туралы білімнің берілмеуі, сол себепті олар шешеді. өз әрекеттерінен хабардар болмай проблемалар. Есептер шығару іс-әрекетіне кіретін іс-әрекетте оқушыларда жеке дағдылар мен дағдылар қалыптаспайды, сондықтан олар бұл әрекеттерді есептерді шешу барысында меңгеруге мәжбүр, бұл көптеген оқушылардың қолынан келмейді. Студенттердің проблемаларды шешудегі белсенділіктерін және олардағы ортақ тәсілдер мен әдістерді, олардың теориялық негіздемесін және түсінуін көрсетуде үнемі талдау жасау ұсынылмайды. Жоғарыда айтылғандарға сүйене отырып, жұмыстың мақсаты геометриялық есептерді шешудің мәні мен құрылымын анықтау, геометриялық есептердің негізгі түрлерін және оларды шешу жолдарын анықтау болып табылады. Осы мақсатқа жету үшін келесі міндеттерді шешу қажет: - тақырып бойынша әдебиеттерді оқу; - тапсырманың құрамдас бөліктерін ерекшелеу; - геометриялық есепті шешудің мәні мен құрылымын анықтау; - геометриялық есептердің негізгі түрлерін және оларды шешу әдістерін анықтау. Зерттеу нысаны геометрия бойынша мектеп курсы болып табылады. Сабақтың тақырыбы геометриялық есептер, олардың негізгі түрлері. Жұмысты орындауда қолданылатын әдістерге: әдебиеттерді талдау, мектеп оқулықтарына әр түрлі авторлар енгізген есептерді талдау, геометриялық есептерді салыстыру, оларды жіктеу, шешу жолдарын жүйелеу жатады. Жұмыс 41 беттен тұрады, кіріспеден, үш тараудан тұрады: I тарау «есептің құрамдас бөліктері», II тарау «Геометриялық есепті шешудің құрылымы мен мәні», III тарау «Есептердің түрлері», қорытынды. , 11 атауы бар библиографиялық тізім, сонымен қатар 11 сызба бар. Бірінші тарауда есептің құрамдас бөліктері, олардың өзара байланысы, схемалық жазбаларға мысалдар келтіріліп, есеп бөліктерін оқшаулау қажеттілігі және схемалық белгілеу негізделеді. Екінші тарауда геометриялық есептің шешу құрылымы, оны құрастыру жолдары берілген. Үшінші тарауда әртүрлі типтегі геометриялық есептерді шешу әдістері қарастырылады. Қорытындылай келе, зерттеу нәтижелері ұсынылады. Жұмысты мұғалім геометрияны оқытуда, студенттер геометриядан емтиханға дайындалуда қолдана алады. I. Тапсырманың құрамдас бөліктері Мәселені шешу - бұл әдеттен тыс жұмыс, атап айтқанда, ой еңбегі. Ал кез келген жұмысты меңгеру үшін алдымен жұмыс істеу керек материалды жақсы оқу керек. Сонымен, есептерді шығаруды үйрену үшін олардың не екенін, қалай орналасатынын, қандай құрамдас бөліктерден тұратынын, есептерді шығаруда қандай құралдар қолданылатынын түсіну керек. Кез келген тапсырманы мұқият қарастырсақ, ол тапсырмада көрсетілген шарттарға негізделіп және ескеріліп, жауабын табу керек болатын талап немесе сұрақ екенін көреміз. Сондықтан кез келген мәселені шешуге кіріскен кезде оны мұқият зерттеп, оның талаптары (сұрақтары) қандай, қандай шарттар негізінде мәселені шешу қажет екенін белгілеу қажет. Мұның барлығы тапсырманы талдау деп аталады. I. 1. Тапсырманы орындау шарттары мен талаптары Әрине, мәселені шешпес бұрын оны мұқият оқып шығу керек. Мәселені оқығанда біз байқайтын бірінші нәрсе - оның белгілі бір талаптары мен бекітулері бар. Көбінесе мәселедегі талап сұрақ ретінде тұжырымдалады, бірақ әрбір сұрақ оған жауап табу талабын білдіреді, сондықтан кез келген сұрақты талаппен ауыстыруға болады. Кез келген тапсырманы тұжырымдау бірнеше мәлімдемелер мен талаптардан тұрады. Есептің қойылымдары есептің шарттары деп аталады (кейде есептің бүкіл қойылымы, яғни шарт пен талаптар бірге) есептің шарты деп аталады. Осыдан-ақ мәселені талдауда ең бірінші мәселенің қойылымын шарттар мен талаптарға бөлу керек екені анық. Мәселенің әдетте бір шарты емес, бірнеше тәуелсіз элементар (төменде бөлінбейтін) шарттары болатынын ескеріңіз; Тапсырмада бірнеше талап болуы мүмкін. Сондықтан есептің барлық қойылымдары мен шарттарын элементарлық шарттар мен талаптарға бөлу қажет. Мысалдарды қарастырыңыз: 1. Тікбұрышты үшбұрышта іштей сызылған шеңбердің жанама нүктесі гипотенузаны ұзындығы 5см және 12см кесінділерге бөледі. Үшбұрыштың катеттерін табыңыз. Бұл есеп «тікбұрышты үшбұрышта іштей сызылған шеңбердің жанама нүктесі гипотенузаны ұзындығы 5 см және 12 см кесінділерге бөледі» делінген. Есептің талабы: «үшбұрыштың катеттерін табу» керек. Келесі қарапайым шарттарды бөліп көрсетуге болады: тікбұрышты үшбұрыш; онда шеңбер жазылған; жанасу нүктесі гипотенузаны екі сегментке бөледі; бір сегменттің ұзындығы 5 см; қалғанының ұзындығы 12 см. Бұл тапсырманың талабын екі негізгі талапқа бөлуге болады: үшбұрыштың бір катетінің ұзындығын табу; үшбұрыштың екінші катетінің ұзындығын табыңыз. 2. Берілген көлемдегі барлық цилиндрлердің ішінен жалпы беті ең кіші цилиндр табылды. Бұл есептің шартын («берілген көлемнің барлық цилиндрлерінен») көлемі белгілі бір V санына тең цилиндрлер жиынтығы қарастырылатындай етіп түсінуге болады (мұнда V – параметр). Есептің талабы – берілген цилиндрлер жиынынан жалпы беті ең кішісін табу. Бұл талапты көрсетілген шартпен байланыстырайық. Қарастырылған цилиндрлердің жалпы беті айнымалы ретінде әрекет ететіні анық. Бұл айнымалының минимумын табуымыз керек. Ол үшін бұл айнымалы басқа айнымалының функциясы ретінде ұсынылуы керек. Соңғысы ретінде сіз цилиндр негізінің радиусын ала аласыз. Сонымен, тапсырманың шарттары келесідей: 1) көлемі V-ге тең цилиндрлер жиынтығы қарастырылады (V – параметр); 2) осы цилиндрлердің табанының радиусы r айнымалысы; 3) бұл цилиндрлердің жалпы S беті қандай да бір функция S(r). Тапсырма талаптары: S(r) функциясын табыңыз; S(r) ең кіші мән қабылдайтын r мәнін табыңыз. Тапсырманы талдаудың оның талаптарына бағытталғандығы да мынада: тапсырма талабының мәнін ашуға, тапсырмада нені табу, не істеу керектігін нақты анықтауға ерекше көңіл бөлу қажет. Кейбір күрделірек есептер үшін жоғарыда қарастырылған талдауды жалғастырған жөн (мәселені жекелеген шарттар мен талаптарға бөлу). Атап айтқанда, оқшауланған жағдайлардың қалай орналасқанын анықтау. Осы шарттарды талдай отырып, олардың әрқайсысы бір немесе бірнеше объектілерден және олардың кейбір сипаттамаларынан тұратынын байқауға болады. Мысалды қарастырайық: Радиустары 4 см және 6 см болатын екі шеңберге өзара перпендикуляр болып шыққан ішкі ортақ жанамалар сызылады. Шеңберлердің центрлерінің арасындағы қашықтықты есептеңіз. Бұл тапсырма келесі шарттарды қамтиды: О1 центрінің шеңбері берілген, оның радиусы 4 см; радиусы 6 см шеңбер басқа О2 центрінен сызылған; бұл екі шеңбер оларға ортақ ішкі жанамаларды тартуға болатындай етіп салынған; осы екі шеңбердің ортақ ішкі жанамалары өзара перпендикуляр. Сонымен бірінші шарттың объектісі шеңбер және оның сипаттамасы: бұл шеңбердің радиусы 4см. Екінші шартта объект сипаттамасы бар шеңбер: оның радиусы 6см. Үшінші шартта екі нысан бар: жоғарыда көрсетілген шеңберлер, ал сипаттамасы олардың жазықтықтағы салыстырмалы орны: олар ішкі ортақ жанамаларды тартуға болатындай етіп орналасады. Ақырында, төртінші шарт екі нысанды қамтиды: шеңберлерге ортақ ішкі жанамалар, олардың қатынасы сипаттама ретінде көрсетілген: олар өзара перпендикуляр. Сонымен, есептің әрбір шартында бір немесе екі (кейбір жағдайларда одан да көп) объект болады; егер күйде бір объект болса, онда оның сипаттамасы осы объектінің қандай да бір қасиеті түрінде көрсетіледі; егер екі объект болса, онда осы объектілердің белгілі бір қатынасы сипаттама қызметін атқарады. Сұрақ туындайды: мәселені шешу үшін мұндай талдау қажет пе? Өйткені, әдетте, есептерді шешу кезінде біз мұндай талдау жасамаймыз. Бірақ біз мұны байқамаймыз, өйткені әдетте мұндай талдау шешім қабылдау барысында ауызша жүргізіледі. I. 2. Есептерді схемалық түрде көрсету Тапсырмаларды алдын ала талдау нәтижелері қандай да бір түрде жазылуы, жазылуы керек. Белгілеудің жоғарыда келтірілген вербальды, сипаттамалық түрі, әрине, өте қолайлы емес. Бізге анағұрлым ыңғайлы, ықшам және сонымен бірге мәселенің талдауын жазудың жеткілікті анық түрі қажет. Мұндай жазба есептің схемалық жазбасы болып табылады. Геометриялық есепті схемалық түрде көрсету үшін есепте қарастырылатын фигураның сызбасын қолданған тиімді. Мұндай сызбаны салу кезінде бірқатар талаптар орындалуы керек. Олардың кейбіреулерін атап өтейік: 1. Сызба фигураның барлық элементтерінің әріптері мен басқа белгілерін пайдалана отырып белгілеуімен тапсырманың негізгі объектісінің (геометриялық фигура немесе фигуралар жиынтығы немесе осы фигуралардың кейбір бөлігі) схемалық сызбасы болуы керек, ал кейбіреулері. оның сипаттамалары. Тапсырма мәтінінде фигураның немесе оның элементтерінің қандай да бір белгілері көрсетілген болса, онда бұл белгілер сызбада да болуы керек; егер мәселеде белгілер болмаса, онда жалпы қабылданған белгілерді пайдалану керек немесе ең қолайлысын ойлап табу керек. 2. Бұл сызба тапсырмаға сәйкес болуы керек. Бұл мәселеде, мысалы, негізгі нысан ретінде үшбұрыш аталса және оның түрі көрсетілмесе (тікбұрышты, тең қабырғалы және т.б.), онда қандай да бір масштабты үшбұрыш салу қажет дегенді білдіреді. 3. Сызбаны салу кезінде қатаң белгіленген масштабты сақтаудың қажеті жоқ. Дегенмен, фигураның жеке элементтерін салу кезінде кейбір пропорцияларды сақтаған жөн. Егер есеп шарты бойынша АВС үшбұрышының АВ қабырғасы ең үлкен болса, онда бұл сызбада сақталуы керек. Немесе үшбұрыштың медианасы берілсе, онда сызбада оған сәйкес кесінді шамамен үшбұрыштың қабырғасының ортасынан өтуі керек және т.б. 4. Кеңістіктік фигуралардың сызбаларын салу кезінде бұл фигураларды салудың барлық ережелерін сақтау қажет. Мүмкін және орынды болса, осы фигуралардың кез келген жазық қималарын салған дұрыс. Геометриялық есептерді схемалық жазу үшін сызбадан басқа есептің барлық шарттары мен талаптарының қысқаша жазбасы да қолданылады. Бұл қысқа жазбада сызбада қабылданған белгілерді пайдаланып, есеп шарттарында көрсетілген барлық сипаттамалар мен қатынастар жазылады. Фигуралар атауын немесе оның жеке бөліктерін олардың анықтамаларының жазбасымен ауыстырған жөн. Мысалы, жазудың орнына: ABCD - трапеция, мынаны жазуға болады: AD || CD. Қысқаша белгілеуде, қажет болған жағдайда стандартты математикалық белгілерді (мүшелік белгісі, қиылысу және т.б.) пайдалануға болады. Сызбалар арқылы геометриялық есептердің схемалық кескіндерін салудың мысалдарын қарастырайық: Трапецияның диагоналы оның табандарына перпендикуляр; үлкенірек табанға іргелес жатқан доғал бұрыш 1200, ал оған іргелес жатқан жағы 7 см; үлкенірек негізі 12 см. Трапецияның орта сызығын табыңыз. Бұл мәселенің негізгі объектісі трапеция болып табылады. Бұл трапецияда диагональ оның табандарына перпендикуляр. Егер сіз бұл трапецияны әдеттегі жолмен, жақтарды салудан бастасаңыз, қателесуіңіз мүмкін. Құрылысты көрсетілген диагональдан бастаған дұрыс. Диагональ екі табанға да перпендикуляр. Оны келесідей көрсетуге болады: Диагональ - тік кесінді, оның ұшынан екі көлденең кесінді (трапеция табандары) әр түрлі бағытта шығады. Бұл диагональ қосатын төбелердің трапециясының бұрыштары екеуі де доғал болуы керек екені анық. Шынында да, есепте үлкен табаны бар бұрыш 1200 болатыны берілген. Енді бұл трапецияны аяқтау қиын емес. Сызбада қабылданған белгіні пайдалана отырып, есептің барлық шарттары мен талаптарын жазамыз. Келесі схемалық белгілерді аламыз (1-сурет): 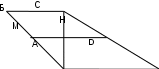 Күріш. 1 Берілген: 1) AB || CD; 2) AB  айнымалы ток; 3) CD айнымалы ток; 3) CD айнымалы ток; 4) айнымалы ток; 4) AM=MD; BN=NC. Табыңыз: MN. II. Геометриялық есепті шешудің мәні мен құрылымы Мәселені шешу тек оның жауабын табу ғана емес. Егер сіз есептің шешімін талдасаңыз, оның жеке қадамдардан тұратынын көруге болады, ал шешудің әрбір қадамы математиканың кейбір жалпы позициясын (ережелер, заңдар, теоремалар, формулалар) есептің жеке шарттарына немесе осы шарттардан алынған салдарларға. II. 1. Геометриялық есепті шығару нені білдіреді Келесі мәселені шешуді қарастырыңыз: Трапецияның табандарының ұзындығы 4см және 10см. Осы трапецияның орта сызығын диагональдарының бірі бөлетін кесінділердің ұзындықтарын табыңыз.. Алдымен осы есептің схемалық бейнесін құрастырайық (2-сурет): 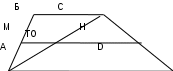 Күріш. 2 Берілген: AB||CD; AM=MD; BN=NC; AB=10см; CD = 4 см. Табыңыз: MK және NK. Шешуі: Трапецияның орта сызығы оның табандарына параллель. Демек, MN||AB және MN||CD. Диагональды айнымалы ток трапецияны екі үшбұрышқа бөледі. Олардың әрқайсысын қарастырайық. ABC үшбұрышында NK кесіндісі ортаңғы сызық болып табылады, өйткені MN кесіндісінің бөлігі ретінде NK AB-ге параллель, ал N нүктесі шарты бойынша ВС қабырғасының ортасы болады. Ал үшбұрыштың орта сызығы оның табанының жартысына тең. Бұл KN=0,5AB дегенді білдіреді, ал содан бері AB \u003d 10 см, содан кейін KN \u003d 5 см. Сол сияқты, ACD үшбұрышын ескере отырып, біз MK үшбұрыштың ортаңғы сызығы екенін анықтаймыз, сондықтан MK \u003d 0,5 CD, бірақ CD \u003d 4 см, сондықтан MK \u003d 2 см. Жоғарыда келтірілген шешім келесі схема түрінде ұсынылуы мүмкін:
Жоғарыда келтірілген мысалдан келесі қорытынды жасауға болады: Геометриялық есепті шешу дегеніміз математиканың жалпы ережелерінің (анықтамалар, аксиомалар, теоремалар, ережелер, заңдар, формулалар) тізбегін табу, оларды есеп шарттарына немесе олардың салдарына (шешудің аралық нәтижелері), Біз мәселеде не талап етілсе, соны аламыз, - деп жауап берді. II. 2. Мәселені шешу процесінің құрылымы Алдыңғы бөлімде біз есептердің шешімдерін жаздық, бірақ бұл шешімдер шешімнің өзін ғана көрсетті. Бірақ бұл шешімдер қалай табылды, олардың дұрыстығына қалай көз жеткіздіңіз? Егер мәселені шешу деп тапсырма алынған сәттен бастап оның шешімін толық аяқтағанға дейінгі процесті түсінетін болсақ, онда, анық, бұл процесс бұрыннан табылған шешімді ұсынудан ғана емес, сонымен қатар бірқатар шешімдерден тұрады. кезеңдері, олардың бірі шешімді ұсыну болып табылады. Мәселені шешу процесінің қадамдары қандай? Тапсырманы алғаннан кейін алдымен оның қандай тапсырма екенін, оның шарттары қандай екенін, оның талаптары қандай екенін анықтау керек, т.б. бірінші тарауда қарастырылғандай мәселені талдаңыз. Бұл талдау мәселені шешу процесінің бірінші кезеңін құрайды. Ол талдау әйтеуір формалдануы, жазылуы керек. Ол үшін әр түрлі схемалық жазбалар қолданылады, олардың құрылысы мәселені шешу процесінің екінші кезеңін құрайды. Мәселені талдау және оның схемалық бейнесін құру негізінен мәселені шешудің жолын табу үшін қажет. Бұл шешімді іздеу мәселені шешу процесінің үшінші кезеңі болып табылады. Мәселені шешудің жолы, оны жүзеге асыру қажет болғанда – бұл мәселені шешу процесінің төртінші кезеңі – шешімді жүзеге асыру (сызбалау) кезеңі болады. Шешім орындалып, айтылғаннан кейін (жазбаша немесе ауызша) бұл шешімнің дұрыстығына, мәселенің барлық талаптарын қанағаттандыратынына көз жеткізу керек. Ол үшін шешім тексеріледі, бұл мәселені шешу процесінің бесінші кезеңі. Көптеген мәселелерді шешу кезінде тексеруден басқа, мәселені зерттеу қажет, атап айтқанда, қандай жағдайда мәселенің шешімі бар екенін және оның үстіне әрбір жеке жағдайда қанша әртүрлі шешімдер бар екенін анықтау; қандай жағдайда мәселенің шешімі мүлде жоқ және т.б. Мұның бәрі мәселені шешу процесінің алтыншы кезеңін құрайды. Шешімнің дұрыстығына көз жеткізіп, қажет болған жағдайда мәселені зерттеуді жүзеге асырып, мәселенің жауабын нақты тұжырымдау қажет - бұл шешім процесінің жетінші кезеңі. Ақырында, білім беру және танымдық мақсаттар үшін аяқталған шешімді талдауға болады, атап айтқанда, басқа, неғұрлым ұтымды шешім бар ма, мәселені жалпылауға бола ма, бұл шешімнен қандай қорытынды жасауға болады және т.б. . Мұның бәрі мәселені шешу процесінің соңғы, әрине, таңдаулы, сегізінші кезеңін құрайды. Есептерді шешу процесінің құрылымы мәселенің сипатына және, әрине, мәселені шешушіде қандай білім мен дағдыларға ие екендігіне байланысты. Есепті шешу процесінің жоғарыдағы диаграммасы тек шамамен алынған. Нақты шешімде бұл кезеңдер әдетте бір-бірінен бөлінбейді, бірақ бір-бірімен араласады. Мәселен, мәселені талдау барысында әдетте шешімді іздеу де жүзеге асырылады. Бұл жағдайда шешімнің жоспары шешімді жүзеге асыру алдында емес, процесте белгіленеді. Содан кейін шешімді іздеу шешім идеясын табумен шектеледі. Қадамдардың реті де өзгеруі мүмкін. Осы сегіз кезеңнің бесеуі міндетті болып табылады және олар кез келген мәселені шешу процесінде (бір немесе басқа түрде) қол жетімді. Бұл мәселені талдау, оны шешудің жолын табу, шешімді жүзеге асыру, шешімін тексеру және жауапты тұжырымдау кезеңдері. Қалған үш кезең (сызбалық белгілеу, мәселені зерттеу және шешімнің соңғы талдауы) міндетті емес. |
