phpyk Аударғаным. Геометриялы есептерді шыаруа йрету
 Скачать 54.83 Kb. Скачать 54.83 Kb.
|
|
Ә.2.Берілген (немесе салынған) екі нүкте арқылы өтетін түзуді тұрғызыңыз. Ә.3.Берілген нүктеден басталып, басқа берілген нүкте арқылы өтетін сәулені тұрғызыңыз. Бір компастың көмегімен келесі негізгі құрылыстарды орындауға болады: C 1. Оның центрі берілген шеңберді және шеңбердің радиусына тең кесіндіні сал. C.2. Шеңбердің центрі мен доғаның ұштарын ескере отырып, шеңбердің қосымша екі доғасының кез келгенін сал. Негізгі құрылыстардан басқа келесі құрылыстар да мүмкін болып саналады: P.1. Берілген екі түзудің қиылысу нүктесін сал. А.2.Берілген түзудің берілген шеңбермен қиылысу нүктесін тұрғыз. Б.3.Берілген екі шеңбердің қиылысу нүктесін сал. P.4. Жазықтықта ерікті түзу сызыңыз. Классикалық құралдардың көмегімен кез келген құрылыс мәселесін шешу қажет болса, онда бұл мәселені шешуді жоғарыда аталған негізгі конструкциялардың реттілігіне дейін азайту жеткілікті. Негізгі конструкциялардан басқа қарапайым геометриялық конструкциялар деп аталатындар да қарастырылады, оларға күрделі конструкциялар қысқарады, яғни. бұл қарапайым құрылыстарды әрқашан жүзеге асыруға болады деп есептеледі және олардың іс жүзінде қалай жүзеге асырылатынын түсіндіру әдеттегідей емес. Элементарлы геометриялық конструкцияларға мыналар жатады: E.1. Бұл кесіндіні екі тең кесіндіге бөліңіз. Е.2.Берілген бұрышты екі тең бұрышқа бөліңіз немесе бұрыштың биссектрисасын салыңыз. Е.3.Берілген түзуде берілген нүктеден берілген бағытта берілгенге тең кесінді сал. Е.4.Берілген нүктеде төбесі бар бұрышты оның берілген жағындағы бұрыштың берілген жағымен және берілген бұрышқа тең етіп тұрғыз. Е.5.Берілген нүкте арқылы және берілген түзуге параллель түзу салу. Е.6.Берілген нүкте арқылы өтетін және берілген түзуге перпендикуляр түзуді салу. Е.7.Үш қабырғасы берілген үшбұрышты тұрғыз. Е.8. Екі қабырғасы және олардың арасындағы бұрыш берілген үшбұрышты тұрғыз. Е.9.Қабырғасы және оған іргелес екі бұрышы берілген үшбұрышты тұрғыз. Е.10.Берілген шеңберге және берілген нүкте арқылы өтетін жанама салу. Е.11.Екі катеті немесе гипотенузасы мен катеті, немесе катеті мен сүйір бұрышы немесе гипотенузасы мен сүйір бұрышы берілген тікбұрышты үшбұрышты сал. Геометриялық құрылыс есептерін шешудің көптеген әртүрлі арнайы әдістері бар. Олардың мәні берілген есептің шешімін негізгі және элементарлық конструкциялар тізбегіне келтіру болып табылады. Мысалдар қарастырыңыз. Үшбұрышты биіктігі, қабырғаларының бірі және табанындағы бұрыштар айырмасы бойынша тұрғызыңыз. Шешуі: алдымен осы элементтерді, қажетті пішінді және оның болуы керек қасиеттерін орнатайық. Бұл элементтер қалаған үшбұрыштың табанына дейінгі биіктігі болатын ерікті h кесіндісі, қалаған үшбұрыштың бүйір жағы болатын ерікті а кесіндісі және табанындағы бұрыштардың айырмасы болатын бұрыш. қалаған үшбұрыш. Қажетті фигура (үшбұрыш) келесі қасиеттерге ие болуы керек: Негізге түсірілген биіктік (және кез келген жағы негіз бола алады) h тең сегмент болуы керек; Қабырғалардың бірі а кесіндісіне тең болуы керек; Үшбұрыштың табанындағы бұрыштар айырымы α бұрышына тең болуы керек. Берілген: екі кесінді h және a, бұрыш α (7-сурет) 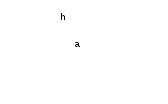 Күріш. 7 Құрылыс мәселесін шешудің жолын табу үшін әдетте келесідей әрекет етеді. Мәселе шешілді деп болжануда, яғни. бұл жағдайда үшбұрыш құрастырылады, онда осы элементтердің барлығы белгіленеді және олар басқа элементтерді тұрғызудың жолын немесе бұл мәселені негізгі және элементар түрлендіруге дейін азайту жолын іздейді.  Күріш. 8 ABC үшбұрышы қалаған үшбұрыш болсын (8-сурет). Базис ретінде АВ қабырғасын қарастырамыз, онда CD биіктігі берілген биіктік h, ал BC бүйір қабырғасы а болады. Енді берілген α бұрышын белгілеуіміз керек. Ол үшін АВ түбіндегі үлкенінен кішісін алып тастаңыз. Үлкен бұрыш А болсын, онда Бұл элементтер қанағаттандыратын кейбір шарттарды бірден орнатуға болады. h және a сәйкесінше CDB тікбұрышты үшбұрышының гипотенузасы мен катеттері болғандықтан, h < a. α бұрышына келетін болсақ, А және В бұрыштары қандай болса да, олардың айырмашылығы сүйір бұрыш, яғни. α < 900. Берілген элементтерден бірден қалаған үшбұрышты салуға болады ма? Болмайтыны анық. Бірақ біз BCD тікбұрышты үшбұрышында CD катеттері мен BC гипотенузасы деректер екенін көреміз. Сондықтан бұл үшбұрышты салуға болады. Осылайша, В бұрышы анықталады, ал α бұрышын біле отырып, біз ACD үшбұрышын BCD үшбұрышына бекітіп, сол арқылы толық қажетті фигураны тұрғыза аламыз. Құрылысқа көшейік, негізгі және қарапайым түрлендірулердің сандарына сілтеме жасай отырып, құрылыс қадамдарын жазыңыз (әрине, бұл балалардан талап етілмеуі керек). 1.E.11. ВС = а гипотенузасына және CD = h катетіне тік бұрышты BCD үшбұрышын саламыз. 2.E.4. Біз 3.E.6. BE┴ жұмсайықД.Б. 4.E.4. Біз 5.E.4. . Біз Алынған A1BC және A2BC үшбұрыштары қалаған үшбұрыштар болып табылады. Дәлелдеу. 1) Осы үшбұрыштардың әрқайсысында A1B және A2B табанына түсірілген CD биіктігі берілген h кесіндісінің құрылысы бойынша тең. 2) Осы екі үшбұрыштың әрқайсысында ВС бүйір қабырғасы құрылысы бойынша берілген а кесіндісіне тең. 3) Енді A1B немесе A2B табанындағы бұрыштар айырмашылығын қарастырайық. А1ВС үшбұрышында ең үлкен бұрыш А1 бұрышы. Сонда < A1 - < B = (900 - < A1CD) - < B = (900 - < MBE) - < B = < MBA1 - < B = < CBM = α. А2ВС үшбұрышында үлкен бұрыш В бұрышы, сондықтан <В - <А2 айырмасын тауып, оның да α-ға тең екенін дәлелдейміз. Зерттеу: Берілген бес құрылыс сатысын қандай жағдайда орындауға болатынын анықтайық. h < a және α < 900 шарттарындағы алғашқы үш қадамды әрқашан орындауға болады. Ал соңғы екі қадам қосымша зерттеулерді қажет етеді, өйткені. олардың әрқайсысы екі конструкциядан тұрады: көрсетілгенге тең бұрыш салу (тиісінше <МБЕ және <НБЕ) және алынған сәуленің BD түзуімен қиылысу нүктесін салу. Көрсетілгенге тең бұрышты салу әрқашан мүмкін, бірақ алынған сәуленің түзу сызықпен қиылысу нүктесін табу үшін зерттеу қажет. Егер VM сәулесі CVE бұрышының ішінен өтсе, онда төртінші қадам әрқашан орындалатын болады. Егер VM көрсетілген бұрыштан тыс өтсе, онда үш жағдай болуы мүмкін (9-сурет): \ 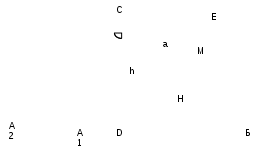 Күріш. 9 BM BM BE оң жағына өтеді, осылайша Егер BM BE-мен сәйкес келсе, онда A1BC үшбұрышы DCB үшбұрышымен сәйкес келеді. Содан кейін шешім ретінде тікбұрышты үшбұрыш аламыз. Біз сондай-ақ бесінші қадамды қарастырамыз. Егер BN сәулесі Сонымен, α және В бұрыштарының арасындағы әртүрлі қатынас үшін есептің шешімі жоқ, бір шешімі және екі шешімі болуы мүмкін. III.2. Есептеуге арналған геометриялық есептер. Геометриялық есептеу тапсырмаларына кез келген элементтің мәнін немесе көрсетілген геометриялық фигураның немесе фигуралар жиынының элементтерінің қатынасын, фигураның кейбір элементтерінің өлшемдерін, фигураның элементтері арасындағы немесе фигуралардың өздері арасындағы қатынасты, егер олардың бірнешеуі болса, белгілі. Мысалды талдап көрейік: Тікбұрышты үшбұрыш гипотенузасы c-ға тең R радиусы бар шеңберге сызылған. Үшбұрыштың периметрін табыңыз. Есепті талдау: 1) есептің нысаны екі фигураның қосындысы: шеңбер және тікбұрышты үшбұрыш; 2) бұл элементтер: шеңбердің радиусы және тікбұрышты үшбұрыштың гипотенузасы; 3) керекті элементтер: үшбұрыштың периметрі; 4) берілген қатынас: тік бұрышты үшбұрыш шеңбердің жанында сызылған. Қиық конустың бір табанының радиусы екіншісінің радиусынан 4 есе үлкен. Конустың биіктігі тең үш бөлікке бөлініп, табандарына параллель бөлу нүктелері арқылы жазықтықтар жүргізілген. Көлем қандай қатынасқа бөлінеді? Есепті талдау: 1) есептің объектісі кесілген конус. Бірақ ол негіздерге параллель жазықтықтармен бөліктерге бөлінеді. Әлбетте, бұл бөліктер де кесілген конустар. Демек, есептің объектісі төрт кесілген конустардың жиынтығы болып табылады, олардың біреуі негізгі, ал қалған үшеуі оның бөліктері болып табылады. 2) осы баптар: жоқ. 3) ізделетін элементтер: жоқ. 4) бұл қатынастар: а) негізгі конус табандарының радиустарының қатынасы; б) кіші қиық конустардың табандарымен бөлінген конус биіктігі бөліктерінің қатынасы - негізгі кесілген конустың бөліктері; қажетті арақатынастар: кесілген конустардың көлемдерінің қатынасы - негізгі конустың бөліктері. Есептеулер үшін геометриялық есептерді шығару процесі әдетте келесідей құрастырылады. Мәселені ауызша талдау жоғарыда көрсетілген схема бойынша жүргізіледі. Талдау негізінде есептің схемалық жазбасы құрастырылады, оның ішінде проблемалық объектінің сызбасы. Содан кейін қажетті элементтерді немесе қатынастарды табу үшін формулалар жазылады және қолда бар деректерге сүйене отырып, осы формулалар арқылы қажеттілерді есептеуге болатынын анықтайды. Егер жоқ болса, онда кейбір сегменттерді немесе бұрыштарды табу үшін мәселені азайту керек және сызбада осы сегменттер немесе бұрыштар кіретін фигураларды (әдетте үшбұрыштар) табу керек. Сонымен бірге бұл қажетті элементтердің деректермен бірге бірдей сандарға қосылуын қамтамасыз ету қажет. Егер бұлай болмаса, онда көмекші элементтер мен фигуралар енгізіледі немесе салынады, бұл ақыр соңында бұған қол жеткізуге мүмкіндік береді. Көбінесе сіз іздеген мәселенің белгілі бір элементін табу процесі келесідей көрінеді: осы қажетті элементті есептеу үшін формула жазылады; бұл элементтер осы формулаға ауыстырылады; егер бұдан кейін формулада айнымалы элементтер қалмаса, онда қажеттісі осы формула бойынша есептеледі және бұл осы қажетті элементтің процесін аяқтайды; егер айнымалы элементтер екінші қадамнан кейін формулада қалатын болса, онда бірінші - үшінші қадамдар олардың әрқайсысы үшін қайталанады және қалағанды табу процесі аяқталғанша осылай жалғасады. Жоғарыда келтірілген есептің мысалы арқылы іздегенімізді табу үшін геометриялық есептерді шығару процесін көрсетейік: Тікбұрышты үшбұрыш гипотенузасы c-ға тең R радиусы бар шеңберге сызылған. Үшбұрыштың периметрін табыңыз. Шешуі: есептің схемалық бейнесін құрастырайық. 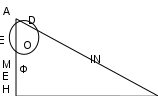 Күріш. 10 Берілген: OD = OE = OF = R; AB = c; Табу: АВС үшбұрышының периметрі. 10-суретте D, E және F нүктелері сипатталғанның жанасу нүктелері болып табылады Берілген радиусы R шеңбері бар ABC тікбұрышты үшбұрышы. Содан кейін OE┴AC және OF┴BC. Демек, OECF төртбұрышында үш E, C және F бұрыштары дұрыс, сондықтан EOF бұрышы дұрыс, ал OE = OF, шеңбердің радиустары ретінде, онда бұл төртбұрыш шаршы болады. Қажетті элементті табуға көшейік. Анықтама бойынша, P \u003d AB + AC + BC, біз бұл элементтерді ауыстырамыз, біз аламыз: P \u003d c + AC + BC. Формулада айнымалы элементтер қалды, яғни біз шешу процесін жалғастырамыз, яғни. АС және ВС айнымалы элементтерін есептеу формулаларын табу. Суреттен сіз мыналарды жаза аласыз: AC \u003d AE + EC, BC \u003d BF + FC (1). Дәлелденген төртбұрышқа сәйкес OECF шаршы болып табылады, сондықтан EC = FC = OE = R. (1) орнын ауыстырыңыз: AC = AE + R, BC = BF + R (2). AE және BF кесінділерінің ұзындығын табу керек. Оларды ABC үшбұрышы шеңбер бойымен шектелген жағдайдан табуға болады: AE \u003d AD және BF \u003d BD бір нүктеден тартылған жанамалардың сегменттері ретінде. (2) орнын ауыстырыңыз: AC = AD + R, BC = BD + R (3). Табылған АС және ВС өрнектерін (3) периметрлік формулаға ауыстырамыз: Р = с + (AD + R) + (BD + R) = с + 2R + (AD + BD) = 2c + 2R, AD және DB сегменттерінің қосындысы AB гипотенузасы болып табылады. Жауабы: 2(c+R). III.3. Дәлелдеуге арналған геометриялық есептер. Кез келген дәлелдеу мәселесінің талабы мәселеде тұжырымдалған кейбір бекітуді дәлелдеу болып табылады. Ол нені білдіреді? Өмірде дәлелдеу көбінесе мәлімдемені тексеру ретінде түсініледі. Бірақ ғылымда тексеру мен дәлелдеу бір-бірімен байланысты болғанымен екі түрлі нәрсе. Мысалы, есепте ромбтың биіктіктерінің тең екендігін дәлелдеу қажет болғанда, биіктіктерді қандай да бір ромбқа салып, олардың тең немесе тең еместігін өлшеу арқылы тексерсек, онда бұл тексерудің оң нәтижесі, Әрине, бұл мәлімдемені негізді етеді, бірақ әлі дәлелденбеген. Оны дәлелдеу үшін катеттері сызылған биіктіктерге тең тік бұрышты үшбұрыштарды қарастырамыз. Олардың гипотенузалары ромбтың қабырғаларындай және сүйір бұрыштары ромбтың қарама-қарсы бұрыштарындай болғандықтан, бұл үшбұрыштар белгілі критерий бойынша тең. Ал тең үшбұрыштарда сәйкес элементтер тең болады. Демек, сызылған ромбтың биіктіктері тең. Бұл дәлелдеудің мәні математикада бұрын дәлелденген және қабылданған тұжырымдардың осындай тізбегін құрастыру болып табылады, оның тікелей логикалық салдары дәлелденуі керек тұжырым болып табылады. Жалпы айтқанда, тұжырымды дәлелдеу - бұл тұжырымның ғылымда дәлелденген және қабылданған тұжырымдар жүйесінің логикалық нәтижесі екенін көрсету. Дәлелдеудің әрбір қадамы әдетте келесі құрылымға ие: 1) бұрын дәлелденген немесе қабылданған жалпы мәлімдеме; 2) мәселенің жағдайы; 3) есептің берілген шартына осы тұжырымды қолданудың логикалық нәтижесі. Мысалы, жоғарыда келтірілген дәлелдеудегі қадамдардың бірі мына болды: қарастырылып отырған үшбұрыштардың гипотенузалары ромбтың қабырғаларына тең. Бұл қадамның құрылымы мынадай: 1) жалпы тұжырым: ромбтың қабырғалары тең; 2) шарт: қарастырылып отырған үшбұрыштардың гипотенузалары ромбтың қабырғалары; 3) логикалық нәтиже? Бұл үшбұрыштардың гипотенузалары тең. Осындай қадамдардан құрастырылған дәлелдеу тікелей дәлелдеу деп аталады. Дәлелдеу есебінің шешімі әдетте тікелей дәлелдеу түрінде беріледі. Бірақ тікелей дәлелдерді дереу табу, әдетте, сәтсіздікке ұшырайды. Дәлелдеуді табу процесі әдетте шарттардан талапқа емес, керісінше талаптан шарттарға қарай кері ретпен құрылады. Мұны мысалмен көрсетейік. Тең бүйірлі трапеция диагональдарының қиылысу нүктесі мен бүйір қабырғаларының созылуының қиылысу нүктесі арқылы анықталатын түзу трапеция табандарына перпендикуляр және оларды екіге бөлетінін дәлелдеңдер.. Шешуі: ABCD табандары AB және CD болатын тең қабырғалы трапеция болсын (11-сурет). 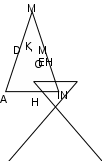 Күріш. он бір Трапецияның О нүктесінде қиылысатын АС және BD диагоналдарын саламыз және қабырғалары М нүктесінде қиылысқанша жалғастырамыз. M және O нүктелері арқылы трапеция табандарымен К және К нүктелерінде қиылысатын MO түзуін жүргіземіз. Н. Дәлелдеуіміз керек: 1) OM┴DC; 2) OM┴AB; 3) DK=KC; 4) AN=BN. Суретке мұқият қарасақ, дәлелдеуге жататын тұжырымдар мынаны білдіретінін көреміз: MK және MN сәйкесінше DCM және ABM үшбұрыштарының биіктіктері мен медианалары. Бұған қалай сенімді бола аласыз? Әрине, біз тең қабырғалы үшбұрыштардың биіктіктері мен медианалары туралы теореманы еске түсіреміз (егер берілген трапеция тең қабырғалы болғандықтан ғана). Осы теоремаға сүйенетін болсақ, онда біріншіден, ABM және DCM үшбұрыштары тең қабырғалы, екіншіден, MN және MK осы үшбұрыштардың биссектрисасы екенін дәлелдеуіміз керек. Үшбұрыштардың тең қабырғалы екенін дәлелдеу үшін олардың табанындағы бұрыштардың тең екендігін дәлелдеу жеткілікті. Бірақ тең қабырғалы трапецияда табандардағы бұрыштар тең. Ал MN және MK сәйкес үшбұрыштардың биссектрисасы екенін дәлелдеу үшін. Үшбұрыштардың теңдігін дәлелдеу керек, оларға AMN және BMN бұрыштары кіреді. Мысалы, AOM және BOM үшбұрыштарының теңдігін дәлелдеуге болады. Бұл үшбұрыштарда MO ортақ қабырға, AM және VM қабырғалары ABM тең қабырғалы үшбұрышының қабырғаларына тең. Сондықтан әлі де болса AO=OB екенін дәлелдеу қажет. Мұны AOB үшбұрышын қарастырып, AOB және OBA бұрыштарының тең екендігін дәлелдеу арқылы дәлелдеуге болады. Ал мұны, өз кезегінде, ABD және ABC үшбұрыштарының теңдігінен (үш жағында) дәлелдеуге болады. Енді бұл есептің шешімін тікелей дәлелдеу түрінде тұжырымдауға болады. Тең қабырғалы трапецияда табандағы бұрыштар тең, сондықтан Егер үшбұрыштың екі бұрышы тең болса, онда үшбұрыш тең қабырғалы болады. AVM үшбұрышында дәлелденген бұрыштар негізінде негізге тең, сондықтан AMB үшбұрышы тең қабырғалы және AM = VM. DM = AM - AD, CM = MB - CB, бірақ MA = VM дәлелденген, ал AD = CB тең қабырғалы трапецияның қабырғалары ретінде, сондықтан AD = CM, яғни. DCM үшбұрышы тең қабырғалы. ABD және ABC үшбұрыштары үш қабырғасында тең (AD=BC – тең қабырғалы трапецияның қабырғалары, AC=BD – тең қабырғалы трапецияның диагональдары, АВ – ортақ қабырға), демек, AOM және BOM үшбұрыштары үш қабырғасында тең (OM – ортақ қабырға, жоғарыда дәлелденген AM=MB, AO=OB жоғарыда дәлелденген), сондықтан Тең қабырғалы үшбұрыштың табанына қарама-қарсы төбесінен жүргізілген биссектрисасы биіктік пен медиана болып табылады. AMB және DCM үшбұрыштары тең қабырғалы, ал MK және MN олардың биссектрисалары, демек OM┴AB, OM┴DC және DK = KC, AN = NB. Қорытындылай келе, есептерді шешуді үйрену үшін не істеу керек екенін қорытындылайық. Біріншіден, біз тапсырмаларды өздері талдауды үйренуіміз керек. Бұл тапсырманы қарапайым шарттар мен талаптарға бөле білу керек дегенді білдіреді. Және әрбір элементарлық жағдайда объектіні және оның сипаттамаларын көру; егер шартта бірнеше объект болса, онда олардың байланысын (байланысты) табыңыз. Сондай-ақ әрбір талаптың (сұрақтың) сипатын белгілеу және сол арқылы тапсырманың түрін анықтау қажет. Ережені ұстанған пайдалы: мәселенің толық, терең талдауы жасалмайынша, оның схемалық көрінісі салынбайынша, қажет болса, шешімнің өзінен өтпеңіз. Екіншіден, кез келген геометриялық есептің шешімі белгілі бір білімді (негізінен математикалық) осы есептің шарттарына дәйекті түрде қолдану, сол арқылы осы шарттардан осындай салдарлар алынғанша салдарларды (аралық шешімдер) алу екенін жақсы түсіну керек. , тапсырманың талаптарына (сұрақтарына) жауаптар болып табылады. Ал бұл нәтижелерге жету үшін математика курсынан алған барлық білімді (анықтамалар, формулалар, теоремалар) жақсы есте сақтау керек. Үшіншіден, есептерді шешудің негізгі әдістерін қолдана білу керек. Және олардың үшеуі ғана бар: тапсырманы қосалқы тапсырмаларға бөлу, тапсырманы модельдеу (түрлендіру) және көмекші элементтер әдісі. Тапсырманы алғаннан кейін, оны талдап, оның схемалық көрінісін құрастырғаннан кейін (қажет болса), келесі ретпен әрекет ету керек: 1.Егер тапсырманы қарапайым қосалқы тапсырмаларға бөле алсаңыз. Сонымен қатар, бірқатар жағдайларда оның ішкі тапсырмаларын берілген тапсырмадан бірінен соң бірін оқшаулай отырып, бөлуді дәйекті түрде орындауға болады. 2. Күрделі тапсырманы қосалқы тапсырмаларға бөлу мүмкін болмаса, оны мүмкіндігінше қарапайым, таныс формаға түрлендіру қажет. 3. Егер тапсырманы ішкі тапсырмаларға бөлмеу, оны қарапайым формаға айналдырмау мүмкін болмаса, онда қосалқы тапсырмаларға бөлуге болатын тапсырманы алу үшін немесе оны түрлендіру үшін кейбір көмекші элементтерді енгізу керек. қарапайым формада. Қорытынды Бұл жұмыста есептің құрамдас бөліктері бөлектеліп, есепті шешудің мәні мен құрылымы айқындалып, геометриялық есептердің негізгі түрлері және оларды шешу әдістері көрсетілген. Зерттеу барысында мынадай қорытындылар жасалды: баланы есептерді шешуге үйрету үшін мәселенің мұқият зерттеу объектісі ретінде әрекет ететін мәселеге осындай көзқарасты және оны шешуді үйрету қажет. - жобалау және өнертабыс объектісі ретінде. Жұмыстың нәтижесі геометриялық есептердің қасиеттерін таңдау болып табылады, олар бойынша есептің әрбір құрамдас бөлігі және әртүрлі типтегі есептерді шешу процесінің әрбір кезеңі жақсы қадағаланады, бұл мұғалімге де, студенттерге де сабаққа дайындалуда көмектеседі. 9-сыныпта таңдау емтиханы және 11-сыныпта USE. Библиографиялық тізім Александров Л.Д.Геометрия 6-8. М.: Білім, 1982 ж. Атанасян Л.С. Геометрия 7-9. М.: Білім, 1996 ж. Атанасян Л.С. Геометрия 10-11. М.Білім, 2002 ж. Погорелов А.В. Геометрия 7-9. М.: Білім, 1996 ж. Медяник А.И.Мұғалімге мектептегі планиметрия курсы туралы. Мәскеу: Білім, 1984 ж. Дышинский Е.А. Үшбұрыш пен шеңбердің геометриясы. Пермь, 1993 ж. Корешкова Т.А. Математика. Жаттығу тапсырмалары. М.: Ағарту. Эксмо, 2006 ж. Денищева Л.О., Безрукова Г.К., Бойченко Е.М. Бірыңғай мемлекеттік емтихан: Математика: 2004 - 2005. М .: Білім, 2005. Фридман Л.М., Турецкий Е.Н. Мәселені шешуді қалай үйренуге болады. Мәскеу: Білім, 1984 ж. Калягин Ю.М., Оганесян В.А. Проблемаларды шешуді үйреніңіз. Мәскеу: Білім, 1984 ж. Никольская И.Л., Семенов Е.Е. Біз дәлелдеуді және дәлелдеуді үйренеміз. Мәскеу: Білім, 1989 ж. |
