phpyk Аударғаным. Геометриялы есептерді шыаруа йрету
 Скачать 54.83 Kb. Скачать 54.83 Kb.
|
|
II. 3.1. Стандартты және стандартты емес тапсырмалар Есептің тікелей шешімі кезекті қадамдардан (әрекеттерден) тұрады, олардың әрқайсысы математиканың қандай да бір жалпы позициясын есептің шарттарына немесе олардың салдарына қолдану болып табылады. Сондықтан осы қадамдарды табу мәселені шешу үшін ең маңызды нәрсе болып табылады. Математика сонымен қатар көптеген есептер үшін ережелерді белгілеумен айналысады, оның көмегімен берілген типтегі кез келген есепті шешу үшін қадамдар тізбегін орнатуға болады. Мұндай тапсырмалар стандартты деп аталады. Стандартты есептердің көптеген түрлері үшін мұндай ережелер бұрыннан табылған. Математикадағы бұл ережелер әртүрлі формада айтылады. 1.Ереже – анықтама: тікбұрышты үшбұрыштың сүйір бұрышының синусы – қарама-қарсы катеттің гипотенузаға қатынасы. Осы жерден синусты (демек, бұрышты) табу реті түсінікті: қарама-қарсы катетті табыңыз, гипотенузаны табыңыз, қатынасты табыңыз. 2. Ереже – теорема: трапецияның орта сызығы оның табандарына параллель және олардың жарты қосындысына тең. Шешу бағдарламасы қарапайым: негіздердің ұзындығын орнатыңыз, олардың жарты қосындысын табыңыз. Бұл трапецияның ортаңғы сызығының ұзындығы болады. Стандартты есептерді шешу процесінің келесі ерекшеліктері бар: 1) Тапсырманы талдау берілген тапсырма жататын тапсырмалар түрін анықтауға (түрін тануға) дейін қысқарады. 2) Шешімді іздеу жалпы ереже немесе жалпы ереже негізінде бағдарлама – берілген типтегі есептерді шешуге арналған қадамдар тізбегін (егер мұндай бағдарлама математика курсында қарастырылмаса) құрастырудан тұрады. ). Әрине, бұл бағдарламаны жазбаша түрде тұжырымдаудың қажеті жоқ, оны өз санаңызда сипаттау жеткілікті. 3) Стандартты есепті шешудің өзі жалпы бағдарламаны берілген есептің шарттарына қолданудан тұрады. Егер шешу бағдарламасының кейбір қадамдары олардың орындалуы үшін кейбір бағдарламаларды да қажет етсе, онда оларға қатысты бірдей операциялар орындалады. Бұдан шығатыны, стандартты есептерді оңай шешу үшін (және олар негізгі математикалық есептер болып табылады, ал қалғандарының барлығы оларға келтірілген): - математика курсында оқытылатын барлық жалпы ережелерді (формулалар, сәйкестіктер) және жалпы ережелерді (анықтамалар мен теоремалар) есте сақтау (есте сақтау). - сәйкес типтегі есептерді шешу қадамдарының реттілігін бағдарламаларға біріктірілген жалпы ережелерді, сәйкестіктерді, формулаларды, анықтамаларды және теоремаларды қолдана білу. Стандартты емес есептер - бұл математика курсында оларды шешудің нақты бағдарламасын анықтайтын жалпы ережелер мен ережелер жоқ тапсырмалар. Оларды шешудің ерекшеліктерін білу үшін мысалды қарастырайық. Табандары 12см және 20см, диагональдары өзара перпендикуляр болатын тең қабырғалы трапецияның ауданын табыңыз. Шешуі: схемалық белгіні құрастыру. Берілген: 1)AB||CD, 2)AD=BC, 3)AC ┴BD, 4)AB=20 см, 5)CD=12 см. Табу: 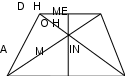 Күріш. 3 Трапецияның ауданын есептеу үшін Str формуласы бар. \u003d 0,5 (a + b) h, мұндағы a және b - трапеция табандарының ұзындығы, ал h - оның биіктігінің ұзындығы. Трапецияның табандары берілген; сондықтан трапецияның биіктігін табу мәселесі қысқарады. Трапецияның биіктігін салайық (3-сурет). Мұны келесідей орындау ыңғайлы: О нүктесі арқылы (диагональдардың қиылысуы) MN┴AB жүргіземіз. Сонда MN - қажетті биіктік h. Өйткені трапеция тең қабырғалы, онда MN трапецияның симметрия осі, сондықтан М және N нүктелері сәйкес табандардың орта нүктелері болып табылады. Трапецияның табандарын біле отырып, AM=10 см, DN 6 см екенін табамыз. Сондай-ақ біз AOM және DON үшбұрыштарын қарастырсақ, олардың тік бұрышты және тең қабырғалы екенін көреміз. Сонда ОМ = AM = 10см, ON = DN = 6см. Демек, h = MN = MO + ON = 10 + 6 = 16 см. Енді көрсетілген формуланы қолдана отырып, біз трапецияның ауданын да есептей аламыз, біз Str. = 256 см2. Бұл мәселені шешу процесі келесі қадамдардан тұрады: трапецияның ауданын есептеу мәселесі трапеция биіктігін табу мәселесіне дейін қысқарды; трапеция биіктігін табу тапсырмасы екі қосалқы тапсырмаға бөлінді: а) MN биіктігінің ОМ кесіндісін табу; б) бірдей биіктіктегі ON кесіндісінің ұзындығын табу; 2 (а, б) тапсырмалары екі тапсырмаға қысқартылды: а) берілген трапецияға қатысты MN түзуінің формасын тану; б) AOM және DON үшбұрыштарының ОМ және ON қабырғаларын анықтау; 3(а) есебін шешу нәтижесінде MN трапецияның симметрия осі екенін анықтадық. Бұл AM және DN, сондай-ақ AOM және DON бұрыштарын табуға мүмкіндік береді; 4 есепті шешу нәтижелері және трапеция диагональдарының перпендикулярлық шарты AOM және DON үшбұрыштарының тік бұрышты және тең қабырғалы екенін анықтауға мүмкіндік береді; Демек, 3 (б) есеп келесіге дейін қысқарады: егер екінші катет белгілі болса, тік бұрышты тең қабырғалы үшбұрыштың катетін табыңыз. 6-мәселені шешіп, 2-есепке, содан кейін бастапқы есепке ораламыз. Кез келген стандартты емес есепті шешу процесі екі негізгі операцияны дәйекті қолданудан тұрады: 1. Стандартты емес тапсырманы басқасына, оған баламалы, бірақ қазірдің өзінде стандартты тапсырмаға қысқарту (түрлендіру немесе қайта құру арқылы). 2. Стандартты емес тапсырманы бірнеше стандартты тапсырмаларға бөлу. Стандартты емес тапсырманың сипатына қарай операциялардың біреуі немесе екеуі де қолданылады. Күрделі есептерді шешу кезінде бұл амалдар бірнеше рет қолданылады. II. 3.2.Тапсырмалар түрін тану. Мәселені шешуді бастағанда, ең алдымен мынаны анықтау керек: мәселе неде? Ол қандай тип? Басқаша айтқанда, сіз мәселенің түрін тануыңыз керек. Өйткені, мәселенің түрін біле отырып, көп жағдайда мәселені шешу әдісін бірден анықтауға болады, өйткені математика курсында есептердің көптеген түрлері үшін оларды шешудің жалпы ережелері бар. Барлық математикалық есептер, демек, геометриялық есептер жеке түрлерге немесе кластарға бөлінетін бірінші белгі есеп талаптарының сипаты болып табылады. Осы негізде тапсырмалар үш сыныпқа бөлінеді: 1. Іздегеніңді табуға арналған тапсырмалар. Бұл сыныптың есептерінде талап - қалағанды табу, тану. Сонымен бірге қажетті мән шама, қатынас, қандай да бір объект, объект, оның орны, пішіні және т.б. Геометриялық есептердің ішінен сегменттің ұзындығын, бұрыштың шамасын, фигураның ауданын, дененің көлемін және т.б. табу керек болатын есептеу есептері кіреді. 2. Дәлелдеуге немесе түсіндіруге арналған тапсырмалар.Бұл сыныптың тапсырмаларында қандай да бір тұжырымның дұрыстығын тексеру немесе бұл тұжырымның дұрыстығын немесе жалғандығын тексеру немесе ол немесе басқа құбылыстың, осы немесе басқа фактілердің неліктен орын алатынын түсіндіру талап етіледі. Талаптары «дәлелдеу», «тексеру» сөздерінен басталатын немесе «Неге?» деген сұрақты қамтитын барлық есептер әдетте осы есептер класына жатады. 3. Түрлендіру немесе салу тапсырмалары.Геометриялық есептердің бұл класына берілген шарттарды қанағаттандыратын қандай да бір фигураны түрлендіру немесе салу қажет болатын есептер жатады. Бұл кластың есептерінің сипатты ерекшелігі олардың әрқайсысында кейбір объектілер көрсетілген, олардан бұрын белгілі қасиеттері бар басқа объектіні құрастыру, тұрғызу қажет. Есептің түрін белгілеу оны шешудің дайын жоспарын алуға мүмкіндік береді: ұқсас есептерді шешу үшін белгілі әдісті қолдану. Әрине, түрін анықтау мүмкін емес тапсырмалар бар, содан кейін басқа әдістерді қолдану керек (мысалы, белгілі типтегі қосалқы тапсырмаларға бөлу). II.3.4. Бұрын шешілген есептерге дейін азайту арқылы мәселені шешу жоспарын табу Атақты кеңес математигі, Мәскеу университетінің профессоры С.Н. Янковская, олимпиада қатысушыларына: «Мәселені шешу дегеніміз не?» деген сұраққа. тыңдаушыларға қарапайым, бірақ күтпеген жауап берді: «Мәселені шешу - оны шешілгенге дейін азайту». Стандартты емес есептерді шешу оларды бұрын шешілген деп санауға болатын стандартты есептерге түрлендіру немесе қайта тұжырымдау арқылы азайтудан тұратынын біз қазірдің өзінде анықтадық. Әрине, бұл кеңес шынайы және қарапайым, бірақ іс жүзінде оны пайдалану оңай емес. Өйткені, бейтаныс мәселелерді таныс, бұрыннан шешілгенге дейін азайтудың нақты ережелері жоқ. Дегенмен, егер сіз мәселені мұқият, ойластырылған талдасаңыз, есептерді шешсеңіз, шешімдерді табудың барлық әдістерін жадқа бекітсеңіз, онда мұндай ақпараттағы дағды біртіндеп дамиды. Мысалды қарастырайық: еркін дөңес бесбұрышта төбелер мен қабырғалар сағат тілінің бағытымен нөмірленген. Бірінші және үшінші жақтардың, сондай-ақ екінші және төртінші жақтардың ортаңғы нүктелері кесінділер арқылы біріктірілген. Сонда осы екі кесіндінің ортаңғы нүктелері де кесінді арқылы қосылады. Бесінші қабырғасының ұзындығы а болса, соңғы кесіндінің ұзындығын табыңыз. Шешуі: Схемалық белгілеуді құрастырайық (4-сурет). 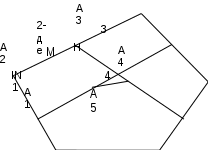 4-сурет Тапсырманың бейтаныс формада екенін көреміз. Оны қандай міндеттерге дейін азайтуға болады? Шартты мұқият оқып отырып, біз тараптардың ортаңғы нүктелері туралы айтып отырғанымызға назар аударыңыз. Қабырғалардың ортаңғы нүктелері үшбұрыштың ортаңғы сызығына, трапецияның ортаңғы сызығына есептер шығарылады. Төртбұрыштың қабырғаларының ортаңғы нүктелерін тізбектей қосу туралы айтатын мәселе де бар. Ал бізге бесбұрыш беріледі. Әрине, бесбұрыштан төртбұрышты кесу идеясы туындайды. Мұны тек жақсы жасау керек. Бұл үшін A1 және A4 шыңдарын қосу ыңғайлы. Алынған A1A2A3A4 төртбұрышында алғашқы үш қабырғасының ортасы В1,В2,В3 нүктелерімен белгіленеді.А1А4 төртінші қабырғасының ортасын С нүктесімен белгілейік (5-сурет). 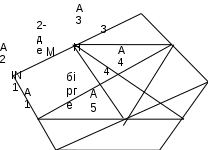 Күріш. 5 А1А2А3А4 төртбұрышының қабырғаларының осы ортаңғы нүктелерін (В1, В2, В3, С нүктелері) тізбектей қосатын болсақ, онда В1В2В3С параллелограммы шығады. Егер бұрын бұл мәселе (төртбұрыштың ортаңғы нүктелерінің тізбектей қосылуы туралы) шешілмесе, онда алынған фигураның параллелограмм екенін дәлелдеу оңай. A2A4 диагоналы төртбұрышты екі үшбұрышқа бөледі. B2B3 - A2A3A4 үшбұрышының ортаңғы сызығы, сондықтан ол A2A4 диагоналына параллель және оның жартысына тең. Сол сияқты, B1C бірдей диагональға параллель және оның жартысына тең. Демек, В1В2В3С В1 төртбұрышының В2В3 және В1С қарама-қарсы қабырғалары параллель және тең. Демек, В1В2В3С В1 төртбұрышы параллелограмм болады. Бұл параллелограммда B1B3 және B2C диагональдары болып табылады және олар қиылысу нүктесінде екіге бөлінген. Бұдан шығатыны, М нүктесі (В1В2 диагоналының ортасы) параллелограммның диагональдарының қиылысу нүктесімен сәйкес келуі керек, сондықтан M да В2С диагоналының ортасы болып табылады. Ал N нүктесі B2B4 ортасы. Сонда MN - CB2B4 үшбұрышының орта сызығы. Бұдан MN = 0,5CB4 болатыны шығады. Ал CB4 - A1A4A5 үшбұрышының ортаңғы сызығы, сондықтан CB4 \u003d 0,5 A1A5 \u003d 0,5a. MN = 0,25a. II.4. Мәселені шешу процестеріндегі модельдеу Модельдеу әдісі ғылымда кеңінен қолданылады. Ол қандай да бір объектіні немесе құбылысты зерттеу үшін зерттелетін объектіге белгілі бір жағынан ұқсас басқа объектінің таңдалуынан немесе салынуынан тұрады. Құрылған немесе таңдалған объект зерттеледі және осы көмек арқылы зерттеу мәселелері шешіледі, содан кейін бұл есептерді шешу нәтижелері бастапқы құбылысқа немесе объектіге беріледі. Көптеген есептерді шешу процесінде осы есептерді модельдеу кеңінен қолданылады. Мысалмен көрсетейік: Конустың көлемі оған сызылған шардың көлемінен екі есе үлкен. Генератрица мен конус табанының жазықтығы арасындағы бұрышты табыңыз. Шешуі: Есептің схемалық бейнесін – конус үлгісін құрастырайық. Ол үшін конус осі арқылы өтетін жазықтықпен іші шар сызылған конустың қимасын саламыз. Бөлімде шеңбер сызылған тең қабырғалы үшбұрышты аламыз (6-сурет). Өйткені бұл үшбұрыштың қабырғасы конустың генератриксі, ал үшбұрыштың биіктігі - конус осі, табан жазықтығына перпендикуляр, содан кейін үшбұрыштың қабырғасы мен табаны арасындағы бұрыш - үшбұрыштың арасындағы қажетті бұрыш генератрикс және негіз жазықтығы. 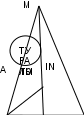 Күріш. 6 Берілген: АВМ – конустың осьтік қимасы; AM = VM; MK┴AB; шеңбер (O, OK) - шардың осьтік қимасы; Vk: Vsh = 2. Табу: Белгілі формулаларды пайдалана отырып, конус пен шардың көлемдерін табамыз: Vk \u003d 1/3ּπAK2 MK; Vsh = 4/3πOK3. Шарт бойынша бізде Vk:Vsh =1/3πAK2 MK: 4/3πOK3 = 2. Біз аламыз: AK2 MK:4OK3 = 2. (1) (1) теңдігіне кіретін барлық кесінділерді AMK үшбұрышынан мынаны табамыз: MK = AK tg AOK үшбұрышынан табамыз: ОК = АК tg Әлбетте, OA MAC бұрышының биссектрисасы, сондықтан OK = ytgx/2. (3) Табылған (2) және (3) өрнектерді (1) орнына қойайық: y2 ytgx:( ytgx/2)3 = 2, аламыз: tgx = 8 tg3x/2. Бұл тригонометриялық теңдеу 00<х<900 болған жағдайда есептің бастапқы шартының үлгісі болып табылады. Бұл теңдеуді осы шарт бойынша шешіп, есептің жауабын табамыз III. Тапсырма түрлері Геометриялық есептердің жалпы түрлерін шешудің негізгі әдістерін қарастырыңыз. III. 1. Құрылысқа арналған тапсырмалар Құрылыс есептері геометрия курсындағы дәстүрлі есептер болып табылады. Ғасырлар бойы математиктер құрылыс есептеріне қызу қызығушылық танытты. Бұл мәселелерге қызығушылық олардың әдемілігі мен шешу әдістерінің өзіндік ерекшелігімен ғана емес, сонымен қатар олардың үлкен практикалық құндылығымен де байланысты. Құрылысты жобалау, сәулет, әртүрлі жабдықтарды жобалау геометриялық конструкцияларға негізделген. Әдетте, құрылыс тапсырмасы берілген элементтерден белгілі бір шарттарға сәйкес белгілі бір құралдардың көмегімен фигураны немесе көрсетілген қасиеттерді қанағаттандыратын олардың комбинациясын салу талабы ретінде қойылады. Осылайша, кез келген құрылыс мәселесінде мыналарды ажырату керек: Берілген элементтер және олардың сипаттамалары (проблемалық жағдайлар); Қажетті талапты орындауға болатын құралдар; Көрсетілген қасиеттері бар қажетті фигура (немесе олардың комбинациясы). Мысалды қарастырайық: l түзуі және оның сыртында А нүктесі берілген. Бір циркульді пайдаланып, l осіне қатысты А нүктесіне симметриялы А1 нүктесін салыңыз. Бұл есепте екі элемент бар: l түзуі және А нүктесі. Олардың сипаттамасы (шарты) А нүктесінің l түзуінен тыс болуы. Қажетті фигура А1 нүктесі. Оның келесі қасиеті болуы керек: A1 l түзуіне қатысты А нүктесіне симметриялы. Құралдар көрсетілген - компастар. Құрылыс жұмыстарының өзіндік ерекшеліктері бар: Қажетті фигураның көрсетілген элементтері негізінен көрсетілмейді, тек көрсетілген. Жоғарыда келтірілген есепте l түзуі мен оның сыртындағы А нүктесі берілгені айтылады, бірақ шын мәнінде l түзуі де, А нүктесі де берілмейді. Біз оларды кез келген жерде және кез келген уақытта жасай аламыз. Қарастырылып отырған мәселеде, әрине, бұл маңызды емес. Бірақ мұнда үш жағынан үшбұрыш салу мәселесінде. Бұл жақтар (берілген элементтер) бізге табиғи сегменттер түрінде берілгенде, бұл бір нәрсе. Содан кейін біз осы кесінділерге үшбұрыш салуымыз керек. Бұл үшбұрышты салуға болады және мұны істеу мүмкін емес болуы мүмкін. Екі жағдайда да мәселені шешу осы сәтте аяқталады. Ал бұл аспектілер біз үшін деректер ретінде ғана аталса, іс жүзінде олар табиғи түрде берілмесе, бұл мүлдем басқа мәселе. Содан кейін сіз үш ерікті кесіндіні өзіңіз алып, олардан үшбұрыш салуға тырысыңыз. Бұл жағдайда сәттілік немесе сәтсіздік әлі шешімді аяқтамайды: біз сондай-ақ қандай жағдайда үшбұрышты салуды жүзеге асыра алатынымызды және қай жағдайда болмайтынымызды анықтауымыз керек. Сонымен, құрылыс есебінде берілген элементтер табиғи түрде берілуі мүмкін немесе оларды тек сипаттамаларын көрсете отырып атауға болады. Бірінші жағдайда шешім қажетті фигураның құрылысымен аяқталады; екінші жағдайда, бұл құрылыс мүмкін болатын жағдайларды белгілеу қажет. Демек, құрылыс есептерін шешудің міндетті кезеңі аяқталған шешімнің талдау кезеңі (зерттеу кезеңі) – қалаған фигураны салу болып табылады. ал қайсысы жоқ. Сонымен, құрылыс есебінде берілген элементтер табиғи түрде берілуі мүмкін немесе оларды тек сипаттамаларын көрсете отырып атауға болады. Бірінші жағдайда шешім қажетті фигураның құрылысымен аяқталады; екінші жағдайда, бұл құрылыс мүмкін болатын жағдайларды белгілеу қажет. Демек, құрылыс есептерін шешудің міндетті кезеңі аяқталған шешімнің талдау кезеңі (зерттеу кезеңі) – қалаған фигураны салу болып табылады. ал қайсысы жоқ. Сонымен, құрылыс есебінде берілген элементтер табиғи түрде берілуі мүмкін немесе оларды тек сипаттамаларын көрсете отырып атауға болады. Бірінші жағдайда шешім қажетті фигураның құрылысымен аяқталады; екінші жағдайда, бұл құрылыс мүмкін болатын жағдайларды белгілеу қажет. Демек, құрылыс есептерін шешудің міндетті кезеңі аяқталған шешімнің талдау кезеңі (зерттеу кезеңі) – қалаған фигураны салу болып табылады. Кез келген құрылыс есептерінде қандай да бір геометриялық фигураны салу ғана емес, есепте көрсетілген қасиеттерге ие геометриялық фигураны салу талап етіледі. Сондықтан, қажетті фигураны құрастырғаннан кейін, оның шын мәнінде барлық көрсетілген қасиеттерге ие екеніне көз жеткізу керек екендігі табиғи нәрсе. Құрылыс мәселелерін шешу процесінің бұл кезеңі әдетте дәлелдеу деп аталады, бірақ шын мәнінде бұл шешімді тексерудің әдеттегі кезеңі. Жоғарыда талқыланған тапсырмада конструкцияларды орындау қажет құрал көрсетілген. Дегенмен, әдетте құрылыс тапсырмаларында құралдар көрсетілмейді. Бұл жағдайда құрылысты классикалық деп аталатын құралдарды - бір жақты сызғыш пен циркульді қолдану арқылы жүргізу керек деп болжанады. Әрбір құралдың көмегімен сіз негізгі құрылыстардың шектеулі санын орындай аласыз. Бір жақты сызғышты пайдаланып келесі негізгі құрылыстарды орындауға болады: Ә.1. Берілген (немесе салынған) екі нүктені қосатын кесіндіні тұрғызыңыз. |
