Гидравлика и нефтегазовая гидромеханика 1 (1). Гидравлика и нефтегазовая гидромеханика
 Скачать 420.2 Kb. Скачать 420.2 Kb.
|
Массовый, объемный и весовой расходРасход потока - это количество жидкости, проносимое потоком сквозь живое сечение за единицу времени. Q=V×A где Q - объемный расход, А - площадь живого сечения. Поскольку количество жидкости может измеряться в единицах объема, массы, веса различают: массовый расход m, кг/с объемный расход Q, л/с, м3/с весовой расход G, H/c Формула связи весового, массового и объемного расхода: G=gm=ρgQ где ρ - плотность жидкости, g - ускорение свободного падения При отсутствии притока и оттока жидкости, согласно уравнению неразрывности, расход несжимаемой жидкости остается постоянным. Объемный способ измерения расходаДоступным и точным методом измерения расхода является объемный способ, в котором фиксируется время наполнения нормированной емкости. В системе СИ расход измеряют в м3/с, при нормировании характеристик устройств часто используют величину л/мин, для пересчета величин используйте калькулятор единиц измерения расхода, представленный на нашем сайте. Средняя скорость потокаСреднюю скорость можно определить используя зависимость: V=Q/A где Q - объемный расход, А - площадь живого сечения. Если рассматривать поток, как множество элементарных струек, то следует понимать, что скорость движения жидкости в каждом из потоков может отличаться от среднего значения. Средняя скорость - это абстрактное понятие, которое дает возможность рассматривать поток, как единое целое. Такой подход позволяет решить множество инженерных задач при движении жидкости в трубопроводах, каналах и т.д. Рассчитать скорость при известных значениях расхода и площади можно с помощью калькулятора скорости потока жидкости. 7. Уравнение сплошности или неразрывности (материальный баланс)  Уравнение неразрывности это уравнение материального баланса или иначе закон сохранения массы Если в сплошной среде выделить произвольный объем V , то очевидно Изменение массы во времени Возможно лишь за счет притока жидкости, который равен суммарному массовому расходу жидкости через поверхность s объема V Уравнение Бернулли для потока идеальной жидкостиРассмотрим установившееся движение потока идеальной несжимаемой жидкости, на которую действует только одна массовая сила - сила тяжести. Выбреем два живых сечения , 1-1 в начале рассматриваемого участка, 2-2 - в конце. 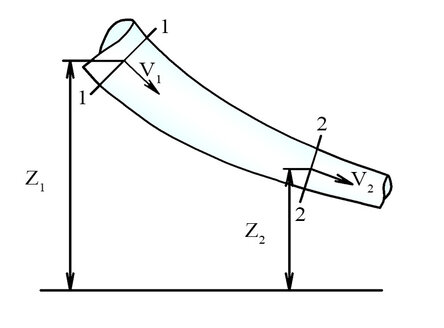 Запишем для этого случая уравнение, связывающее между собой скорость движения жидкости и ее давление в каждом сечении. z1 + (p1/ρg) + (V12/2g) = z2 + (p2/ρg) + (V22/2g) где z - геометрическая высота, p - давление в выбранном сечении, V - скорость жидкости в выбранном сечении, ρ - плотность жидкости, g - ускорение свободного падения. Указанное уравнение называют законом или уравнением Бернулли для элементарной струйки идеальной несжимаемой жидкости. Для каждого рассматриваемого сечения полный напор есть сумма геометрического, пьезометрического и скоростного напора. Для идеальной жидкости (т.е. при отсутствии потерь энергии) полный напор - величина постоянная. z + p/ρg + V2/2g = Н = const где z - геометрический напор, p/ρg - пьезометрический напор, z + p/ρg - статический напор, V2/2g - скоростной напор, z + p/ρg + V2/2g = Н - полный напор. Уравнение Бернулли можно записать и в другом виде, умножим обе части уравнения на g получим: gz1 + p1/ρ + V12/2 = gz2 + p2/ρ + V22/2 Физический смысл уравнения БернуллиСоставляющие уравнения Бернулли являются различными формами удельной (отнесенной к единице массы) механической энергии жидкости: gz - удельная энергия положения, p/ρ - удельная энергия давления движущейся жидкости, V12/2 - удельная кинетическая энергия жидкости, gz + p/ρ + V2/2 = Hg - полная удельная энергия движущейся идеальной жидкости. Физический и энергетический смысл уравнения Бернулли заключается в постоянстве полной удельной энергии вдоль элементарной струйки идеальной жидкости. Уравнение Бернулли отражает закон сохранения механической энергии для идеальной несжимаемой жидкости. |
