Гидравлика и нефтегазовая гидромеханика 1 (1). Гидравлика и нефтегазовая гидромеханика

• Название: Гидравлика и нефтегазовая гидромеханика
• Анкор: Гидравлика и нефтегазовая гидромеханика
• Дата: 06.05.2023
• Размер: 420.2 Kb.
• Имя файла: Гидравлика и нефтегазовая гидромеханика 1 (1).docx
• Тип: Реферат; #1112480
• страница: 3 из 7

5. Сила гидростатического давления на плоские стенки

Равнодействующая сил давления на плоскую стенку w  определяется по формуле:

F = pсв × w + r × g × hс × w,

где w - площадь смоченной поверхности плоской стенки, м2:

hс - глубина погружения центра тяжести С смоченной площади под уровень свободной поверхности, м;

pсв – внешнее давление (на свободную поверхность жидкости);

Произведение hс × w - это объём цилиндра с площадью основания w и высотой hс.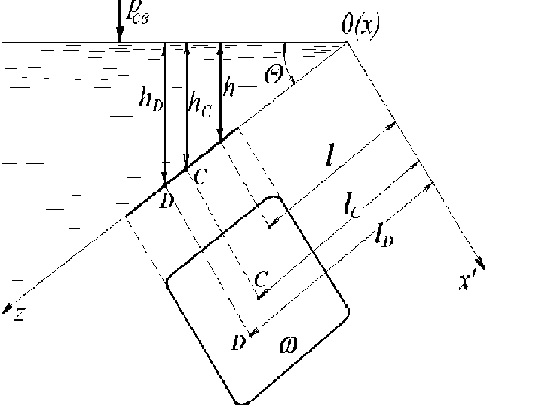




К определению силы давления на плоскую стенку

В уравнении:

pсв × w = Fвн- сила внешнего давления, передаваемая на стенку по закону Паскаля, Н;

r × g × hс × w = Fж - сила давления самой жидкости на стенку, Н.

Следовательно, сила, с которой жидкость давит на плоскую стенку, равна весу жидкости в объёме цилиндра с основанием, равнымплощади данной стенки, и высотой, равной глубине погружения центра тяжести этой площади под уровень свободной поверхности:

Fж = r × g × hс × w.

Так как r × g × hс = рс, где рс – гидростатическое давление в центре тяжести площадки w, можно записать:

Fж = рс × w.

Точка приложения равнодействующей сил давления на наклонную стенку лежит ниже центра тяжести – в центре давления D.

Глубина погружения центра давления под уровень свободной hD поверхности жидкости равна:

hD = lD × sinQ,

lD – расстояние от свободной поверхности до центра давления D, считая по наклону стенки4

Q – угол наклона стенки к горизонту.

Расстояние от свободной поверхности до центра давления D, считая по наклону стенки lD, определяется по формуле:

lD = lС +   ,

где lС – расстояние от свободной поверхности до центра тяжести С, считая по наклону стенки;

IC – момент инерции смоченной площади относительно оси, проходящей через центр тяжести С параллельно линии уреза жидкости.

Совпадать глубина погружения центра тяжести смоченной поверхности С и центра давления D может только в случае, если площадка горизонтальная или она лежит на бесконечно большой глубине.

6. Виды движения жидкостей

Основными видами движения жидкости являются: движение установившееся и неустановившееся, равномерное и неравномерное, напорное и безнапорное, сплошное и прерывистое.

Установившимся движением называется такое движение жидкости, при котором давление и скорость не изменяются во времени в каждой фиксированной точке пространства, через которую проходит жидкость.

,



Движение, при котором скорость и давление изменяются не только от координат пространства, но и от времени, называется неустановившимся или нестационарным

,

.

Примером неустановившегося движения может служить истечение жидкости из отверстия при переменном уровне ее в резервуаре: с понижением высоты столба жидкости скорость истечения уменьшается во времени.

Установившееся движение в свою очередь подразделяется на равномерное и неравномерное.

Равномерным называется такое установившееся движение, при котором живые сечения вдоль потока не изменяются: в этом случае ; средние скорости по длине потока также не изменяются, т.е.  . Примером равномерного движения является: движение жидкости в цилиндрической трубе, в канале постоянного сечения при одинаковых глубинах.

Установившееся движение называется неравномерным, когда распределение скоростей в различных поперечных сечениях неодинаково; при этом средняя скорость и площадь поперечного сечения потока могут быть и достоянными вдоль потока. Примером неравномерного движения может быть движение жидкости в конической трубе или в речном русле переменной ширины.

Напорным называется движение жидкости, при котором поток полностью заключен в твердые стенки и не имеет свободной поверхности. Напорное движение происходит вследствие разности давлений и под действием силы тяжести. Примером напорного движения является движение жидкости в замкнутых трубопроводах (например, в водопроводных трубах).

Безнапорным называется движение жидкости, при котором поток имеет свободную поверхность. Примером безнапорного движения может быть: движение жидкости в реках, каналах, канализационных и дренажных трубах. Безнапорное движение происходит под действием силы тяжести и за счет начальной скорости. Обычно на поверхности безнапорного потока давление атмосферное.

Следует отметить еще один вид движения: свободную струю. Свободной струей называется поток, не ограниченный твердыми стенками. Примером может служить движение жидкости из пожарного брандспойта, гидромонитора, водопроводного крана, из отверстия резервуара и т. п. В этом случае движение жидкости происходит по инерции (т. е. за счет начальной скорости) и под действием силы тяжести.

Для упрощения выводов, связанных с изучением потока жидкости, вводится понятие о плавно изменяющемся движении жидкости.

Плавно изменяющимся называется такое движение жидкости, при котором кривизна струек незначительна (равна нулю или близка к нулю) и угол расхождения между струйками весьма мал (равен нулю или близок к нулю), т. е. практически поток жидкости мало отличается от параллельноструйного. Это предположение вполне оправдывается при изучении многих случаев движения жидкости в каналах, трубах и других сооружениях.

Отметим следующие свойства потока при плавно изменяющемся движении:

1. поперечные сечения потока плоские, нормальные к оси потока;

2. распределение гидродинамических давлений по сечению потока подчиняется закону гидростатики, т.е. гидродинамические давления по высоте сечения распределяются по закону прямой. Это свойство легко можно доказать, если внутри потока выделить частицу жидкости и спроектировать все действующие на нее силы на плоскость живого сечения. Вследствие того, что скорости и ускорения в этом случае будут перпендикулярны сечению, силы инерции в уравнение не войдут; поэтому уравнение равновесия и закон распределения давления в плоскости живого сечения не будет отличаться от такового для жидкости, находящейся в покое;

3. удельная потенциальная энергия (т. е. потенциальная энергия единицы веса жидкости) по отношению к некоторой плоскости сравнения для всех точек данного сечения потока жидкости есть величина постоянная.

Понятие жидкости. Реальная и идеальная жидкости

Жидкость – физическое тело, молекулы которого слабо связаны между содой. Поэтому незначительные силы способны легко изменить форму жидкости, которая способна сохранить объем, но не форму.

В гидравлике жидкость рассматривают как непрерывную среду, заполняющую пространство без пустот и промежутков, т.е. отвлекаются от молекулярного строения жидкости и её частицы, даже бесконечно малые, считают состоящими из большого числа молекул.

Реальной жидкостью называют жидкость, обладающую вязкостью (свойство жидкости сопротивляться сдвигу ее слоев).

Идеальная или невязкая жидкость является упрощенной моделью реальной (вязкой) жидкости. По предположению, идеальная жидкость имеет все свойства реальной, кроме вязкости.