ок. Графы. Поиск количества путей
 Скачать 2.33 Mb. Скачать 2.33 Mb.
|
Ещё пример задания:Р-06 (Д. Муфаззалов). На рисунке – схема дорог, связывающих города А, Б, В, Г, Д, Е, Ж, И, К. По каждой дороге рисунке представлена схема дорог, связывающих города А, Б, В, Г, Д, Е, Ж, З, И, К. По каждой дороге можно двигаться только в одном направлении, указанном стрелкой">можно двигаться только в одном направлении, указанном стрелкой. Сколько существует различных маршрутов из города А в город К, содержащих ровно пять городов, включая города А и К? 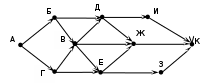  Решение (метод динамического программирования): в целом задача решается так же, как и стандартная (на количество маршрутов любой длины), но приходится для каждого пункта определять число маршрутов всех возможных длин в этот город из исходного пункта для некоторого города X будем обозначать количество маршрутов в виде где Li – возможная длина маршрута в этот город из начального пункта, а ki – количество маршрутов длиной Li; например, запись X:53·62 означает, что из начального пункта в пункт X есть 3 маршрута длиной 5 и 2 маршрута длиной 6 очевидно, что есть только один маршрут из A в A, и он имеет длину 1, то есть A:11 при переходе к следующему пункту длина маршрута увеличивается на 1; количество сохраняется; например, в пункты Б и Г можно попасть только из А, поэтому Б:21, Г:21 . в пункт В можно попасть из Б и Г, поэтому «перемножаем» количество маршрутов для Б и Г, увеличивая длины на 1: В = Б · Г:(2+1)1 · (2+1)1 = 32. Это значит, что в пункт В ведёт 2 маршрута длиной 3. пункт Д доступен из Б и В, поэтому Д = Б · В:(2+1)1 · (3+1)2 = 31 · 42. аналогично Е = Г · В:(2+1)1 · (3+1)2 = 31 · 42. далее определяем количество маршрутов для И (доступен только из Д) и З (доступен только из Е) И:(3+1)1 · (4+1)2 = 41 · 52, З:(3+1)1 · (4+1)2 = 41 · 52 . вершина Ж доступна из Д, В, Е: Ж = Д · В · Е :(3+1)1 · (4+1)2 · (3+1)2 · (3+1)1 · (4+1)2 = = 41 · 52 · 42 · 41 · 52= 44 · 54 наконец, конечная вершина К доступна из Ж, З, И: К = Ж · З · И :(4+1)4 · (5+1)4 · (4+1)1 · (5+1)2 · (4+1)1 · (5+1)2 = 54 · 64 · 51 · 62 · 51 · 62 = 56 · 68. Таким образом, из пункта А в пункт К есть 6 маршрутов, проходящих через 5 городов, и 8 маршрутов, проходящих через 6 городов. Ответ: 6. Ещё пример задания:Р-05. (демо-2021) На рисунке представлена схема дорог, связывающих города А, Б, В, Г, Д, Е, Ж, З, И, К, Л, М. По каждой дороге можно двигаться только в одном направлении, указанном стрелкой. Сколько существует различных путей из города А в город М, проходящих через город В? 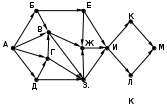 Решение: нас интересуют пути, проходящие через город В, поэтому на первом этапе отсекаем все ребра, которые позволяют на пути от А к М обойти город В; это рёбра БЕ, ГЗ и ДЗ; получается, что вершину Е тоже можно убрать, потому что в неё не ведёт ни одна стрелка; начальную вершину помечаем единицей (1 путь из А в А, никуда не ехать): 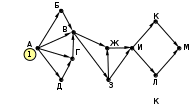 в вершины Б и Д можно ехать только из А, поэтому помечаем их тоже единицами; в вершину Г можно приехать из А (метка 1) и из Д, поэтому метка вершины Г – 2: 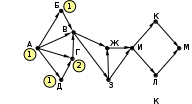 в вершину В можно приехать из Б (метка 1), А (метка 1) и Г (метка 2), так что метка вершины В равна 1 + 1 + 2 = 4: 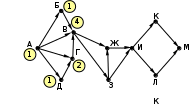 в вершину З можно ехать только из В, поэтому её метка тоже равна 4; для вершины Ж складываем метки В и З (4 + 4 = 8), а для И – складываем метки Ж и З (8 + 4 = 12) 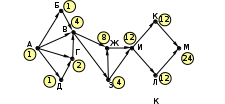 для вершин К и М получаем по 12 путей, а для М - 24 Ответ: 24. Решение (И.В. Степанов): нас интересуют пути, проходящие через город В, поэтому на первом этапе отсекаем все ребра, которые позволяют на пути от А к М обойти город В; это рёбра БЕ, ГЗ и ДЗ; получается, что вершину Е тоже можно убрать, потому что в неё не ведёт ни одна стрелка; 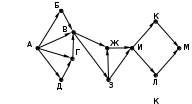 Рассмотрим все пути из А в В, просматривая вершины сверху вниз. Их всего 4: АБВ, АВ, АГВ и АДГВ. Теперь рассмотрим все пути из В в И (узловая точка через которую проходят все дороги в направлении М). Из В в И ведут 3 дороги: ВЖИ, ВЗЖИ, ВЗИ. Теперь остается определить дороги из и в М. Их 2: ИКМ и ИЛМ. Остается определить общее количество возможных путей. По правилу произведения комбинаторики N= 4*3*2=24. Ответ: 24. |
