ок. Графы. Поиск количества путей
 Скачать 2.33 Mb. Скачать 2.33 Mb.
|
|
и последние 2 шага
Ответ: 13. Решение (4 вариант, перебор всех путей с начала, А. Яфарова): запишем все вершины, в которые есть прямой путь из вершины A: Б, В и Г; получается три начальных отрезка: АБ, АВ, АГ рассмотрим маршрут АБ: из Б можно ехать в В и Д, поэтому получаем два маршрута: АБВ, АБД рассматриваем конечные точки этих маршрутов: из В можно ехать в Д и Ж, а из Д – в И и К: АБВД, АБВЖ, АБДИ, АБДК снова смотрим на конечные точки: из Д едем в И и К, из Ж и И – только в К: АБВДИ, АБВДК, АБВЖК, АБДИК, АБДК из И едем только в К, таким образом, все возможные маршруты, содержащие участок АБ, доведены до конечной точки К, всего 5 таких маршрутов: АБВДИК, АБВДК, АБВЖК, АБДИК, АБДК затем аналогично рассматриваем маршруты, которые начинаются с АВ: АВД, АВЖ АВДИ, АВДК, АВЖК АВДИК, АВДК, АВЖК всего 3 маршрута наконец, остается рассмотреть маршруты, которые начинаются с АГ: АГВ, АГЕ АГВД, АГВЖ, АГЕЖ, АГЕК АГВДИ, АГВДК, АГВЖК, АГЕЖК, АГЕК АГВДИК, АГВДК, АГВЖК, АГЕЖК, АГЕК всего 5 маршрутов складываем количество маршрутов для всех начальных участков: 5 + 3 + 5 = 13 Ответ: 13.
Решение (5 вариант, графический, О.О. Грущак, КузГПА): Главную идею решения: (число дорог в город N есть сумма дорог, приводящих в города, из которых есть прямой проезд в город N), отразим на самой схеме, показывая на ней ЧИСЛО ДОРОГ, приводящих в каждый город. Последовательность очевидна: начинаем с Б и Г (городов, куда есть по 1-й дороге из А) 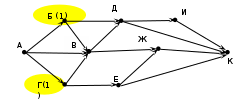 Посчитаем дороги в В: 1 (из A)+ 1(дороги города Б)+ 1(дороги города В)= 3 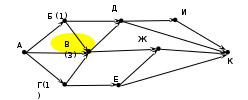 Аналогично посчитаем дороги в Д, И, Е, Ж: 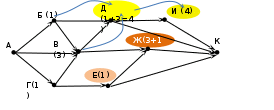 Определяем число дорог в город К, как сумму дорог в города, с которыми он связан: Д, И, Ж, Е. 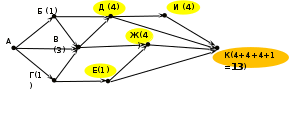 Ответ: 13. |
