ок. Графы. Поиск количества путей
 Скачать 2.33 Mb.
|
Ещё пример задания:Р-01. Города A, B, C и D связаны дорогами. Известно, что существуют дороги между городами A и С, C и B (две дороги), A и B, C и D (две дороги), B и D. Сколькими различными способами можно проехать из города А в город D, не заезжая дважды в один город? Решение: нарисуем граф, в котором множественные дороги из одного города в другой будем обозначать одной дугой и подписывать около неё количество дорог: 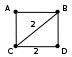 выпишем все маршруты, по которым можно ехать из A в D так, чтобы дважды не проезжать один и тот же город:
теперь рассмотрим маршрут A B D; на всех участках только одна дорога, поэтому есть только один такой маршрут для маршрута A С D: на первом участке только одна дорога, на втором – две, общее число маршрутов равно произведению этих чисел: 1*2 = 2 аналогично находит количество различных путей по другим маршрутам A B С D: 1*2*2 = 4 A C B D: 1*2*1 = 2 всего получается 1 + 2 + 4 + 2 = 9. Ответ: 9. Еще пример задания:Р-00. На рисунке – схема дорог, связывающих города А, Б, В, Г, Д, Е, Ж, И, К. По каждой дороге можно двигаться только в одном направлении, указанном стрелкой. Сколько существует различных путей из города А в город К? 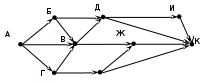  Е Решение (1 вариант, подстановки): начнем считать количество путей с конца маршрута – с города К будем обозначать через NX количество различных путей из города А в город X общее число путей обозначим через N по схеме видно, что NБ = NГ = 1 очевидно, что если в город X можно приехать только из Y, Z, то NX = NY + NZ, то есть нужно сложить число путей, ведущих из A во все города, откуда можно приехать в город X поскольку в K можно приехать из Е, Д, Ж или И, поэтому N = NК = NД + NЕ + NЖ + NИ в город И можно приехать только из Д, поэтому NИ = NД в город Ж можно приехать только из Е и В, поэтому NЖ = NЕ + NВ подставляем результаты пп. 6 и 7 в формулу п. 5: N = NВ + 2NЕ + 2NД в город Д можно приехать только из Б и В, поэтому NД = NБ + NВ так что N = 2NБ + 3NВ + 2NЕ в город Е можно приехать только из Г, поэтому NЕ = NГ так что N = 2NБ + 3NВ + 2NГ по схеме видно, что NБ = NГ = 1, кроме того, NВ = 1 + NБ + NГ = 3 окончательно N = 2NБ + 3NВ + 2NГ = 2·1 + 3·3 + 2·1 = 13 Ответ: 13. Решение (2 вариант, удобная форма записи): начнем считать количество путей с конца маршрута – с города К з  аписываем для каждой вершины, из каких вершин можно в нее попастьК ИДЖЕ И Д Ж ВЕ Е Г Д БВ Г А В АБГ Б А теперь для удобства «обратного хода» вершины можно отсортировать так1, чтобы сначала шли все вершины, в которые можно доехать только из начальной точки А: Б А Г А затем на каждом шаге добавляем те вершины, в которые можно доехать из уже добавленных в список (и из исходной точки): В АБГ Е  Гдалее добавляем все вершины, куда можно доехать из А, Б, Г, В и Е: Д БВ Ж ВЕ на следующем шаге добавляем вершину И И Д и, наконец, конечную. вершину К ИДЖЕ именно в таком порядке мы и будем вычислять количество путей для каждой вершины теперь идем по полученному списку вершин, полагая, что количество вариантов попасть в вершину равно суммарному количеству вариантов попасть в ее непосредственных предшественников. NБ = 1, NГ = 1 NВ = 1+1+1 = 3, NЕ = 1 NД = 1+3 = 4, NЖ = 3 + 1 = 4 NИ = 4, N = NК = 4 + 4 + 4 + 1 = 13 заметим, что вершины можно и не сортировать специально, а просто выбирать возможный порядок вычисления: проверять, какие значения известны и какие можно рассчитать с их помощью на следующем шаге Ответ: 13.
|