ок. Графы. Поиск количества путей
 Скачать 2.33 Mb. Скачать 2.33 Mb.
|
|
© К. Поляков, 2009-2022 13 (повышенный уровень, время – 3 мин)Тема: Графы. Поиск количества путей Что проверяется: Умение представлять и считывать данные в разных типах информационных моделей (схемы, карты, таблицы, графики и формулы). 1.3.1. Описание (информационная модель) реального объекта и процесса, соответствие описания объекту и целям описания. Схемы, таблицы, графики, формулы как описания. 1.2.1. Умение использовать готовые модели, оценивать их соответствие реальному объекту и целям моделирования. Что нужно знать: если в город R можно приехать только из городов X, Y, и Z, то число различных путей из города A в город R равно сумме числа различных путей проезда из A в X, из A в Y и из A в Z, то есть где число путей конечно, если в графе нет циклов – замкнутых путей Пример задания:Р-07 (А. Калинин) На рисунке представлена схема дорог, связывающих города А, Б, В, Г, Д, Е, Ж, З, И, К, Л, М. По каждой дороге можно двигаться только в одном направлении, указанном стрелкой. Определите количество различных путей ненулевой длины, которые начинаются и заканчиваются в городе И, не содержат этот город в качестве промежуточного пункта и проходят через промежуточные города не более одного раза. 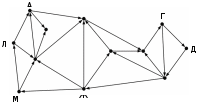 Решение (А. Калинин): из точки И выходят дороги ИА, ИБ, ИК; рассмотрим каждый из этих случаев отдельно старт через ИА (рассматриваются только дороги, ведущие в точку И): 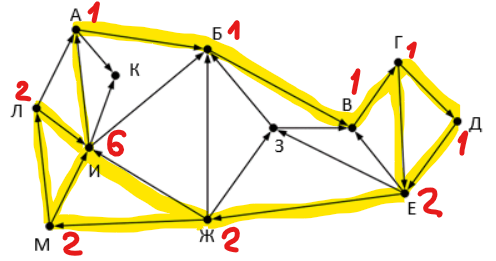 получаем 6 различных путей старт через ИБ (рассматриваются только дороги, ведущие в точку И): 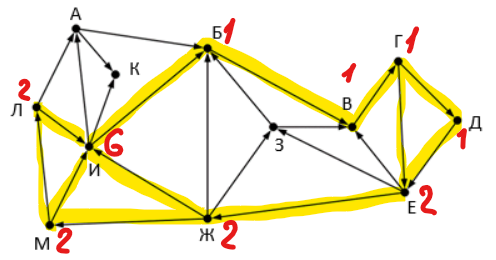 получаем ещё 6 различных путей старт через ИК: эта дорога заводит в тупик: из точки К невозможно пройти ни в один из пунктов складывая количество путей во всех случаях, получаем общее количество различных путей, начинающихся и заканчивающихся в точке И: 6 + 6 = 12. Ответ: 12. Решение (программа на Python): сначала задаём граф в виде списка смежности, данные записываем в словарь, где у каждого элемента ключ – это обозначение вершины, а значение – это список вершин, куда можно прийти за один шаг из данной вершины: G = { 'А': "БК", 'Б': "В", 'В': "Г", 'Г': "ДЕ", 'Д': "Е", 'Е': "ВЖЗ", 'Ж': "БЗИМ", 'З': "БВ", 'И': "АБК", 'К': "", 'Л': "АИ", 'М': "ЛИ", } теперь пишем рекурсивную процедуру, которая перебирает все возможные пути; она будет увеличивать глобальный счётчик count, когда найдёт очередной путь: count = 0 def findPath( path, target ): global count lastTown = path[-1] ... параметр path – это уже построенная часть пути (символьная строка), а параметр target – это конечный пункт; в конце фрагмента мы записываем метку последней вершины в переменную lastTown (потом она будет дважды использоваться) затем проверяем, не пришли ли мы к конечному пункту; если пришли, то увеличиваем счётчик путей и выводим построенный путь на экран: if lastTown == target and len(path) > 1: count += 1 print( path ) return второе условие (len(path) > 1) нужно для того, чтобы процесс поиска сразу не остановился, когда начальный пункт совпадает с конечным (как в нашей задаче) теперь нужно проверить дальнейшие пути через все города, в которые можно проехать из lastTown, эту информацию берём из словаря G, который описывает граф: for town in G[lastTown]: if not town in path or town == target: findPath( path+town, target ) условие в операторе if означает, что мы проверяем возможный путь только тогда, когда новой вершины town еще нет в пройденном маршруте или она совпадает с конечной точкой. приведём полную программу: G = { 'А': "БК", 'Б': "В", 'В': "Г", 'Г': "ДЕ", 'Д': "Е", 'Е': "ВЖЗ", 'Ж': "БЗИМ", 'З': "БВ", 'И': "АБК", 'К': "", 'Л': "АИ", 'М': "ЛИ", } count = 0 def findPath( path, target ): global count lastTown = path[-1] if lastTown == target and len(path) > 1: count += 1 print( path ) return for town in G[lastTown]: if not town in path or town == target: findPath( path+town, target ) findPath( 'И', 'И' ) print( count ) Ответ: 12. |
