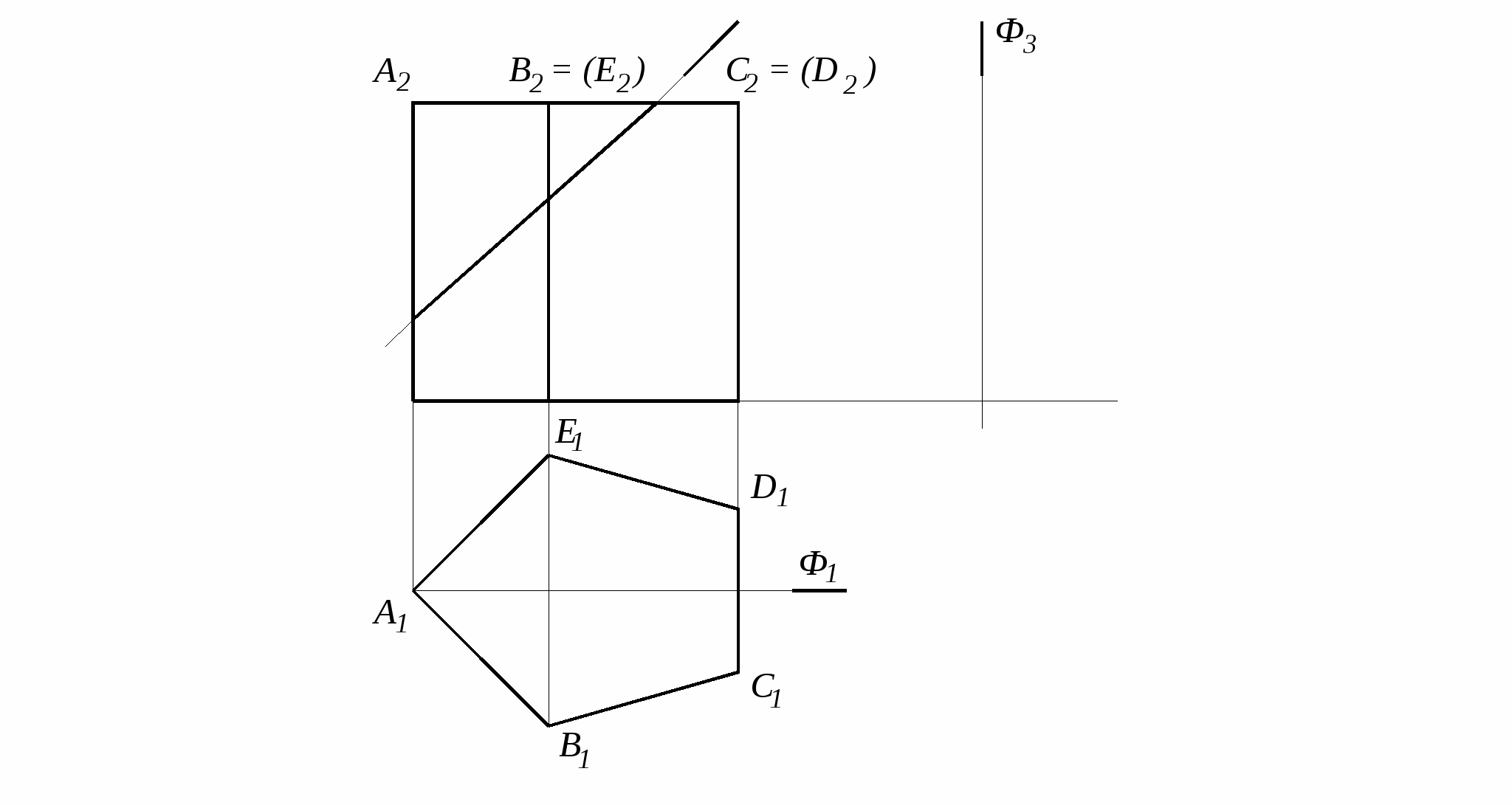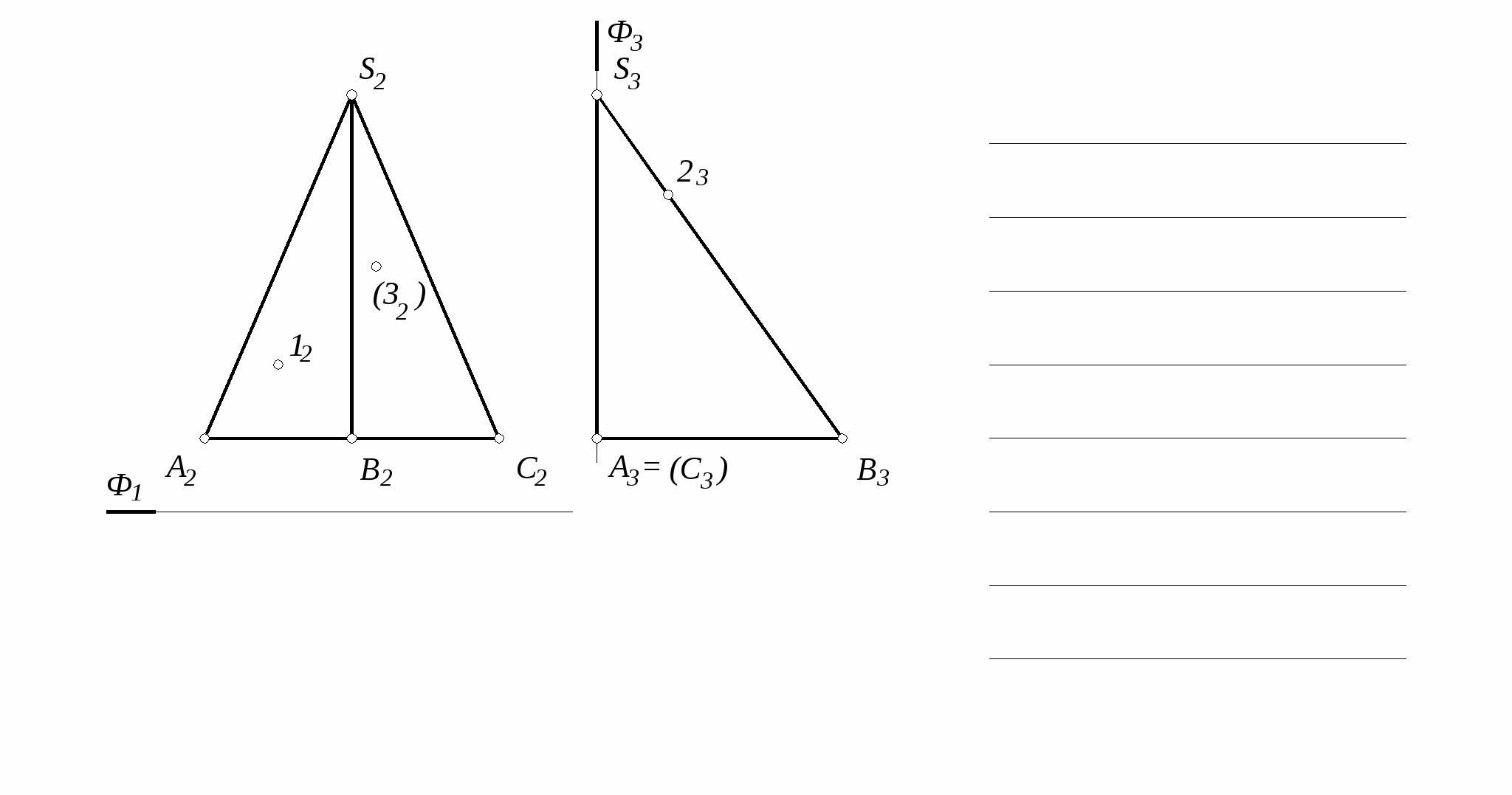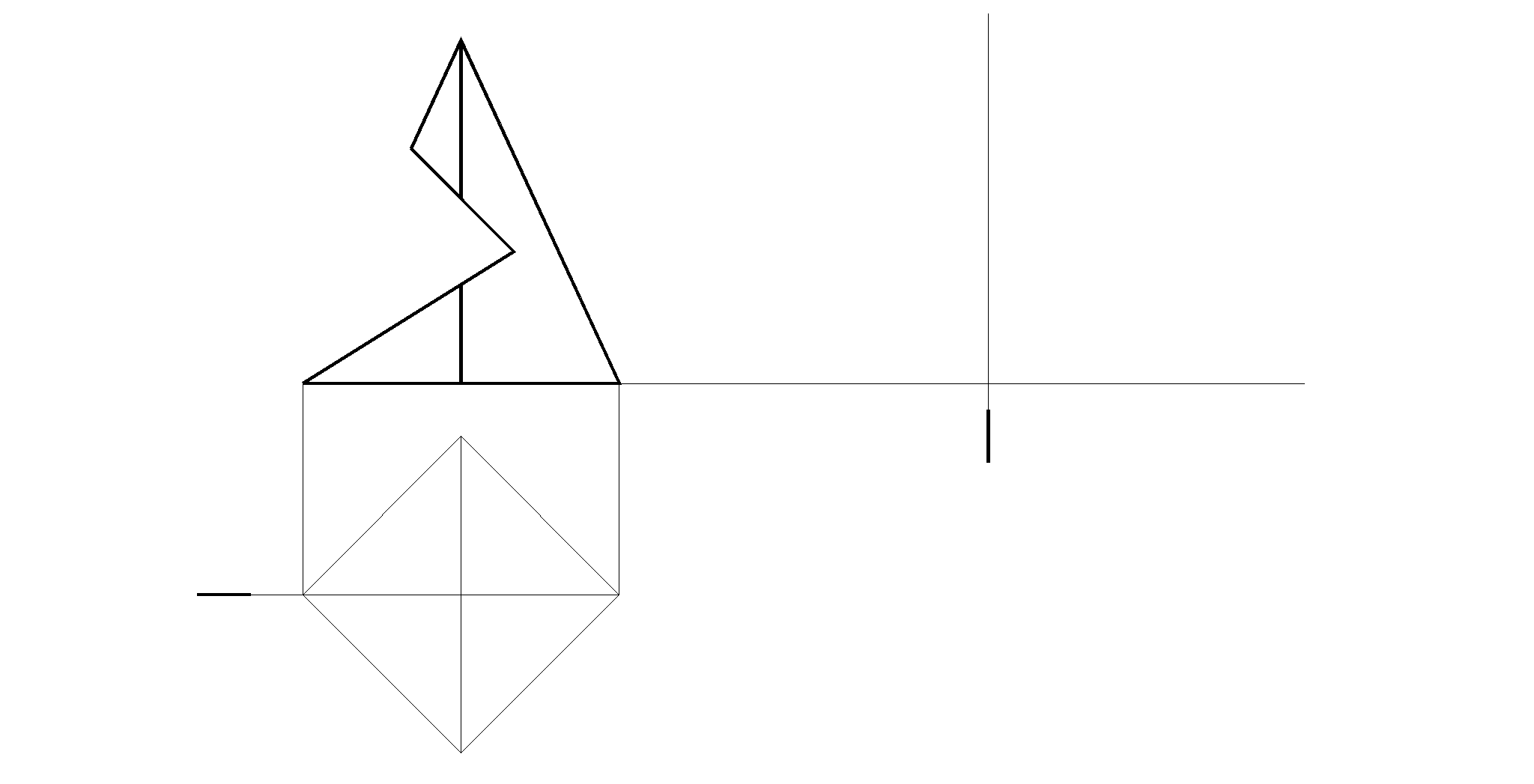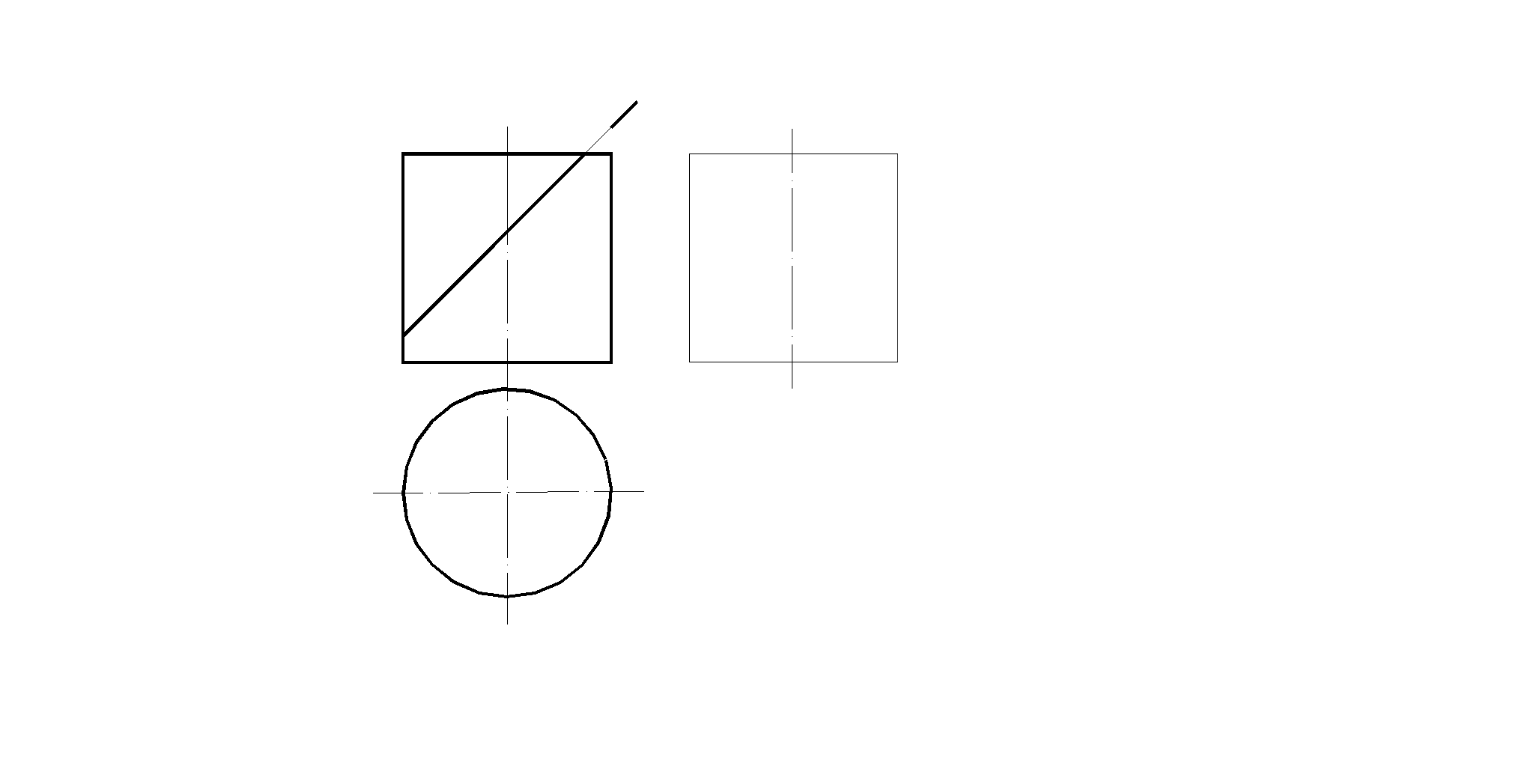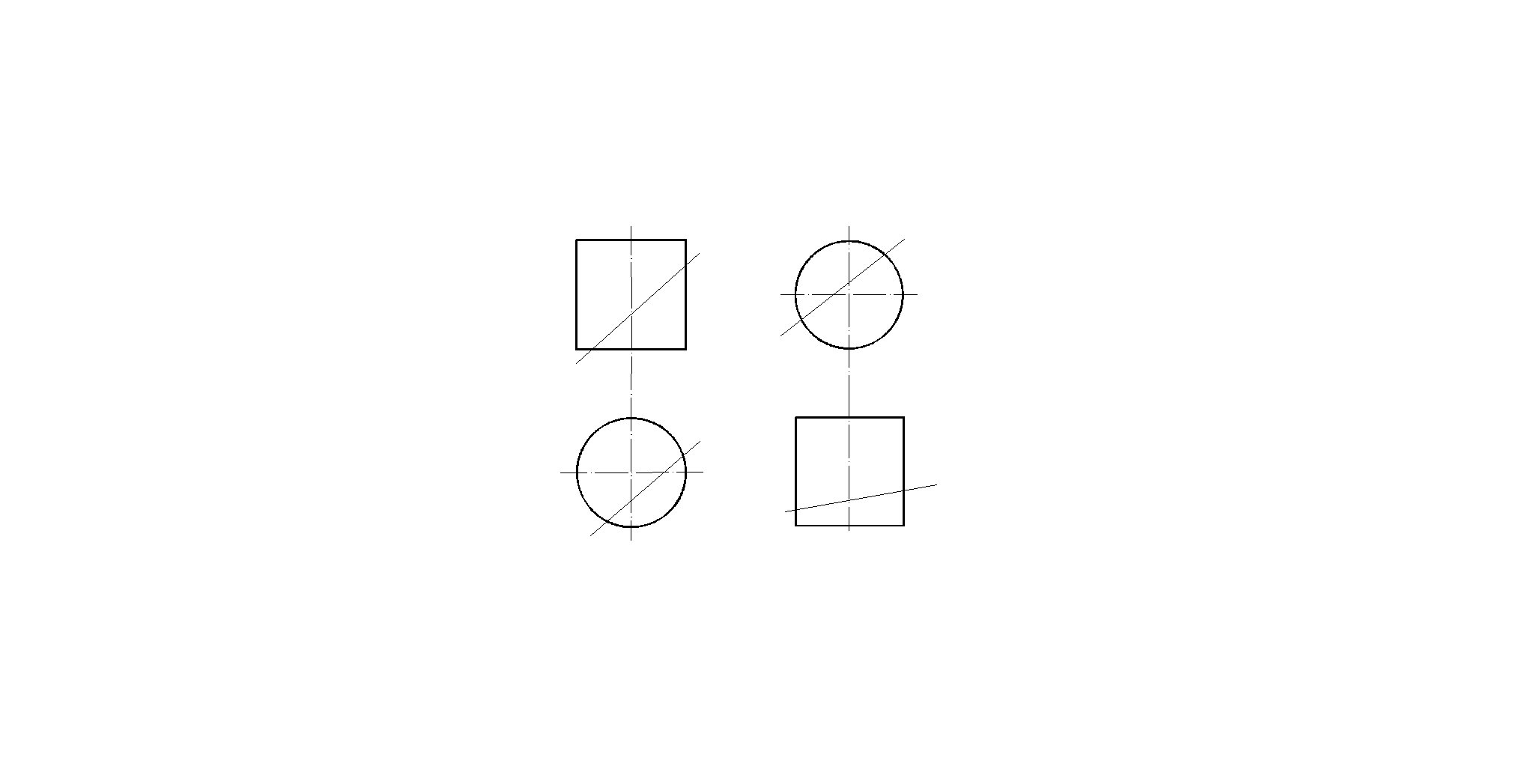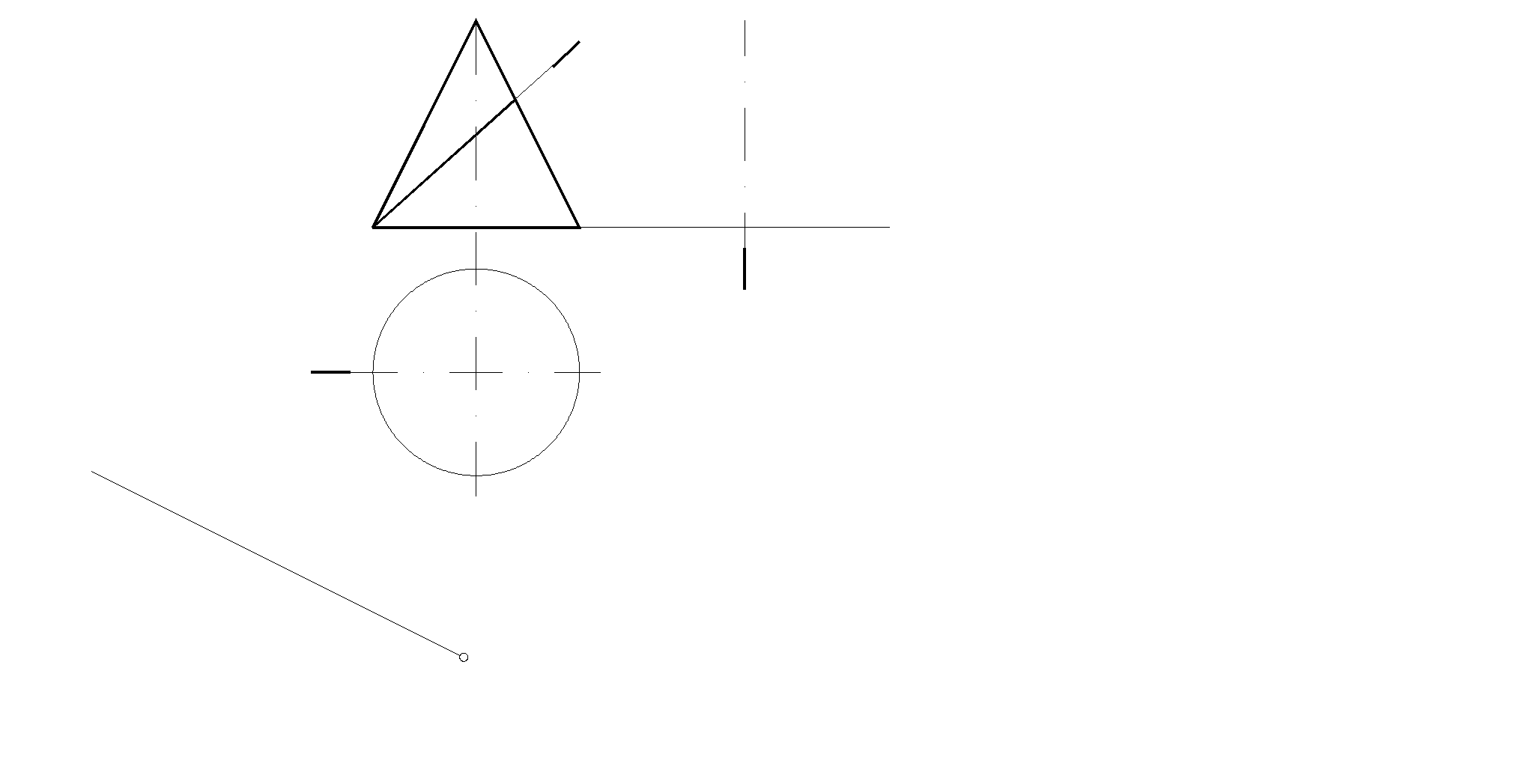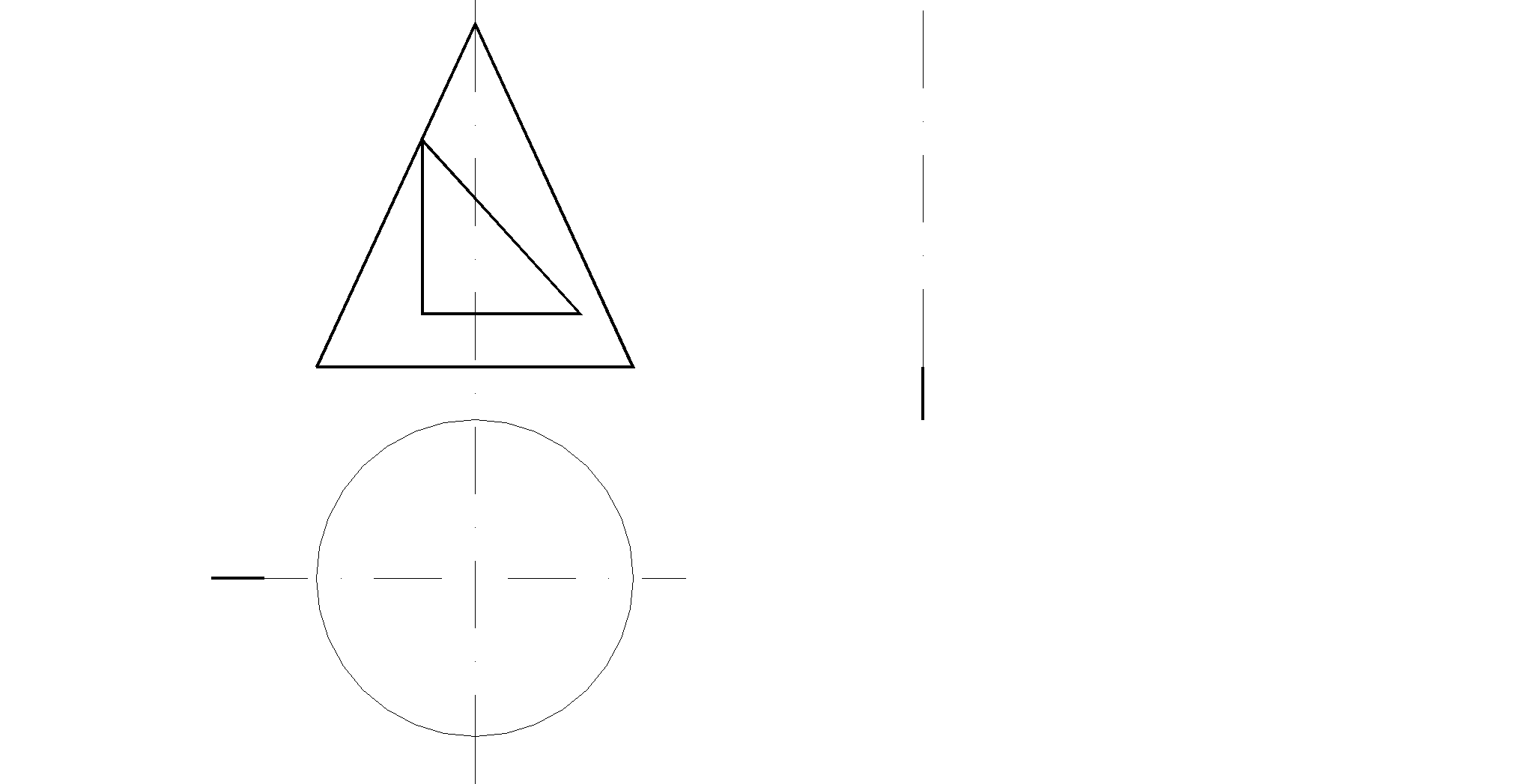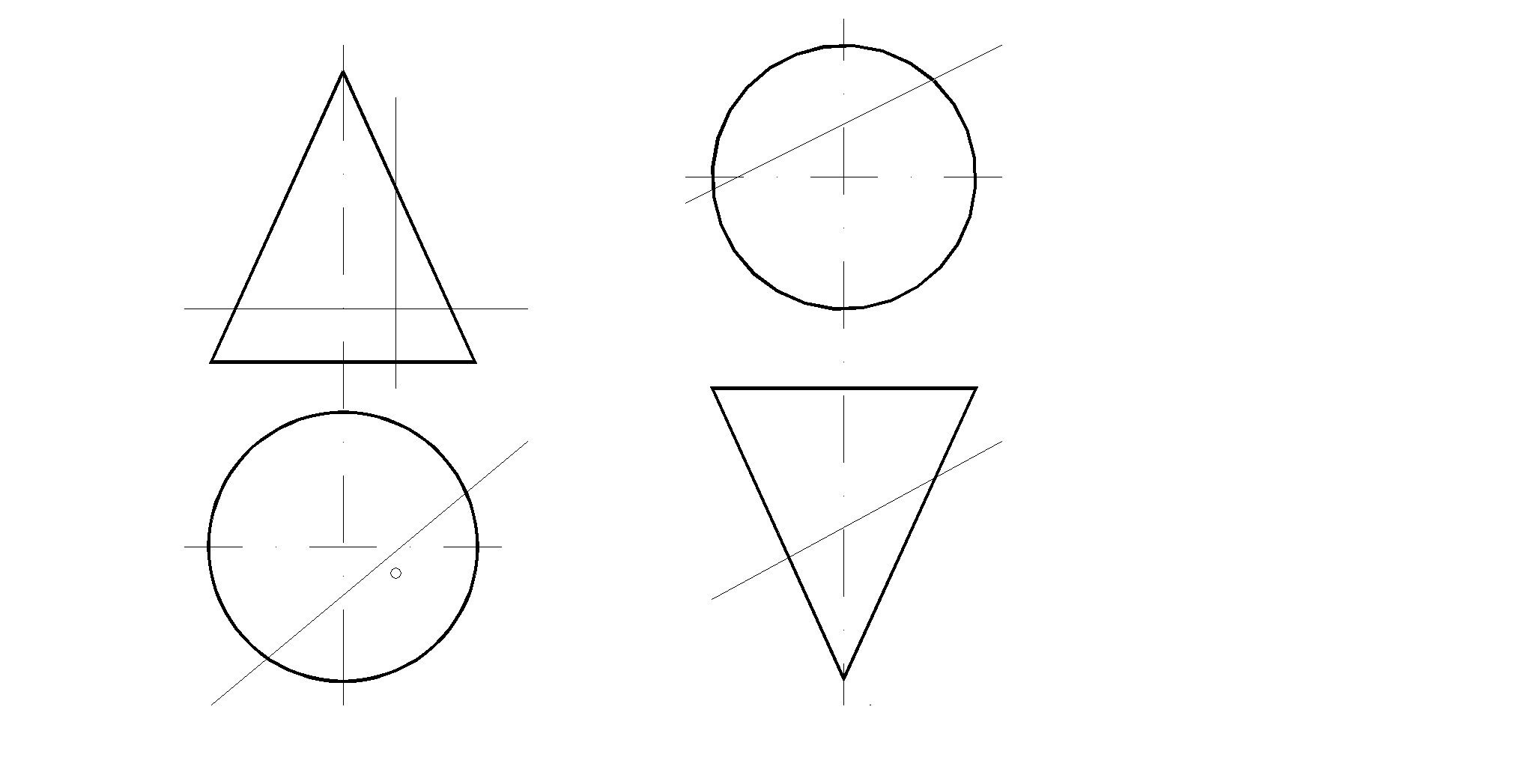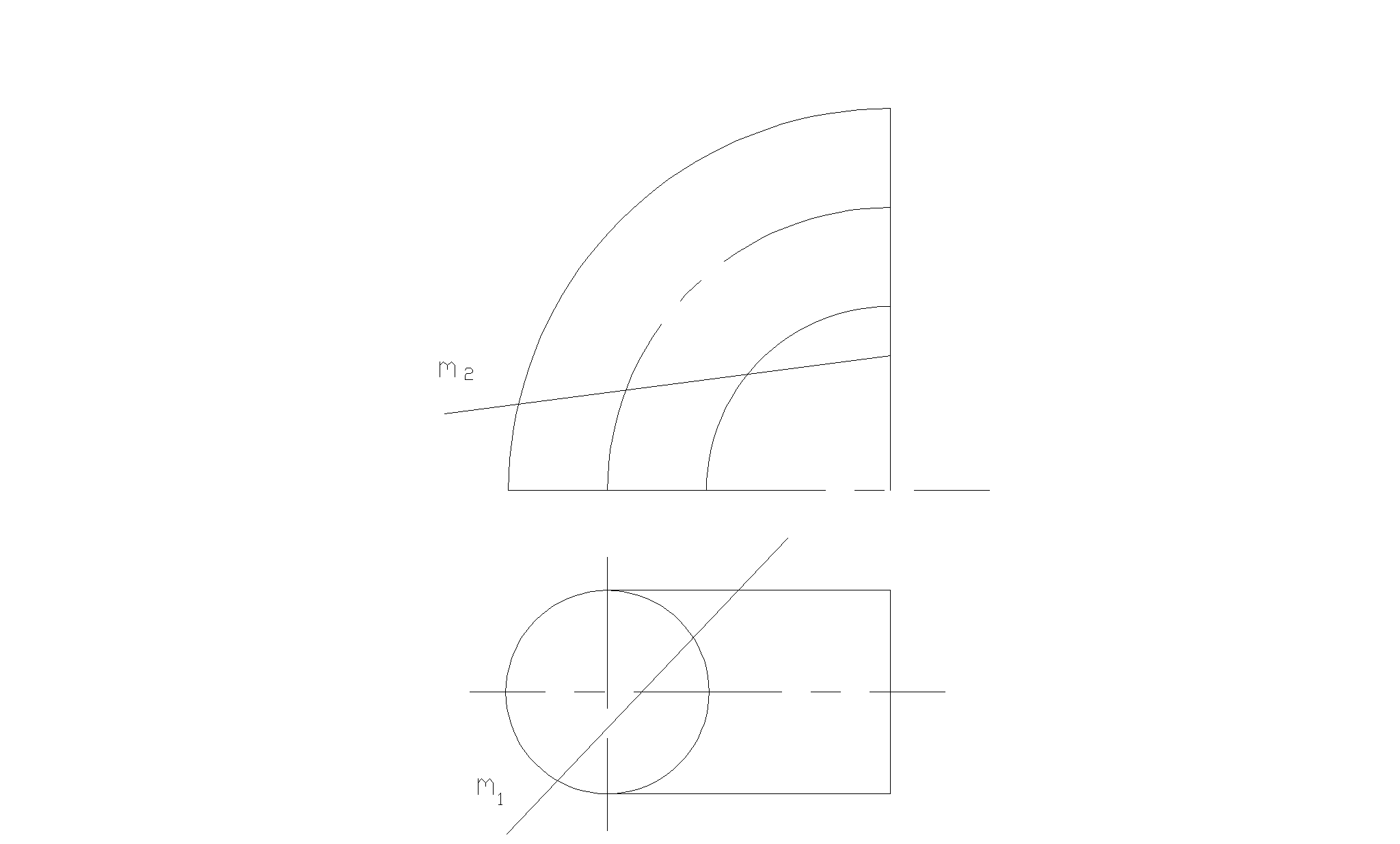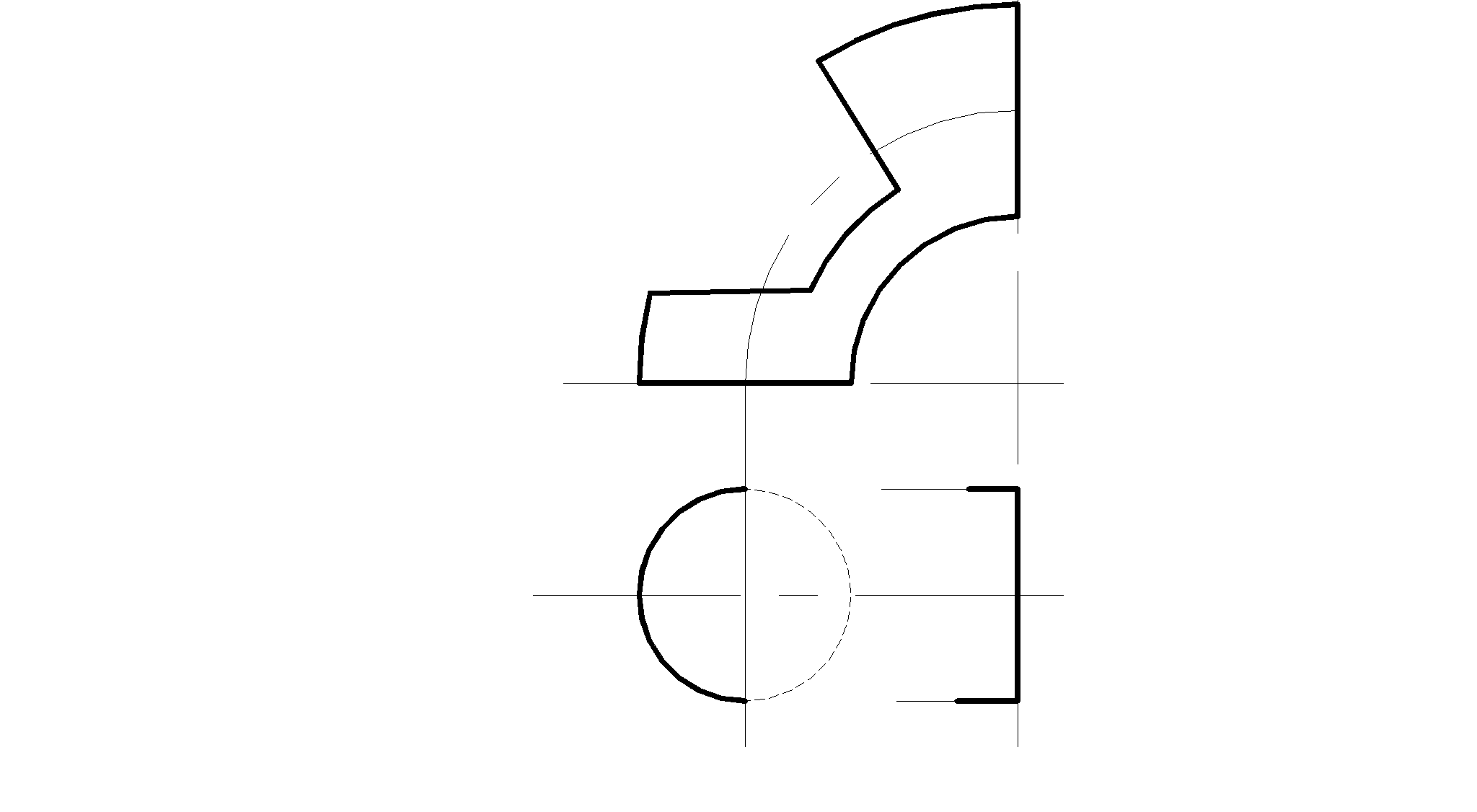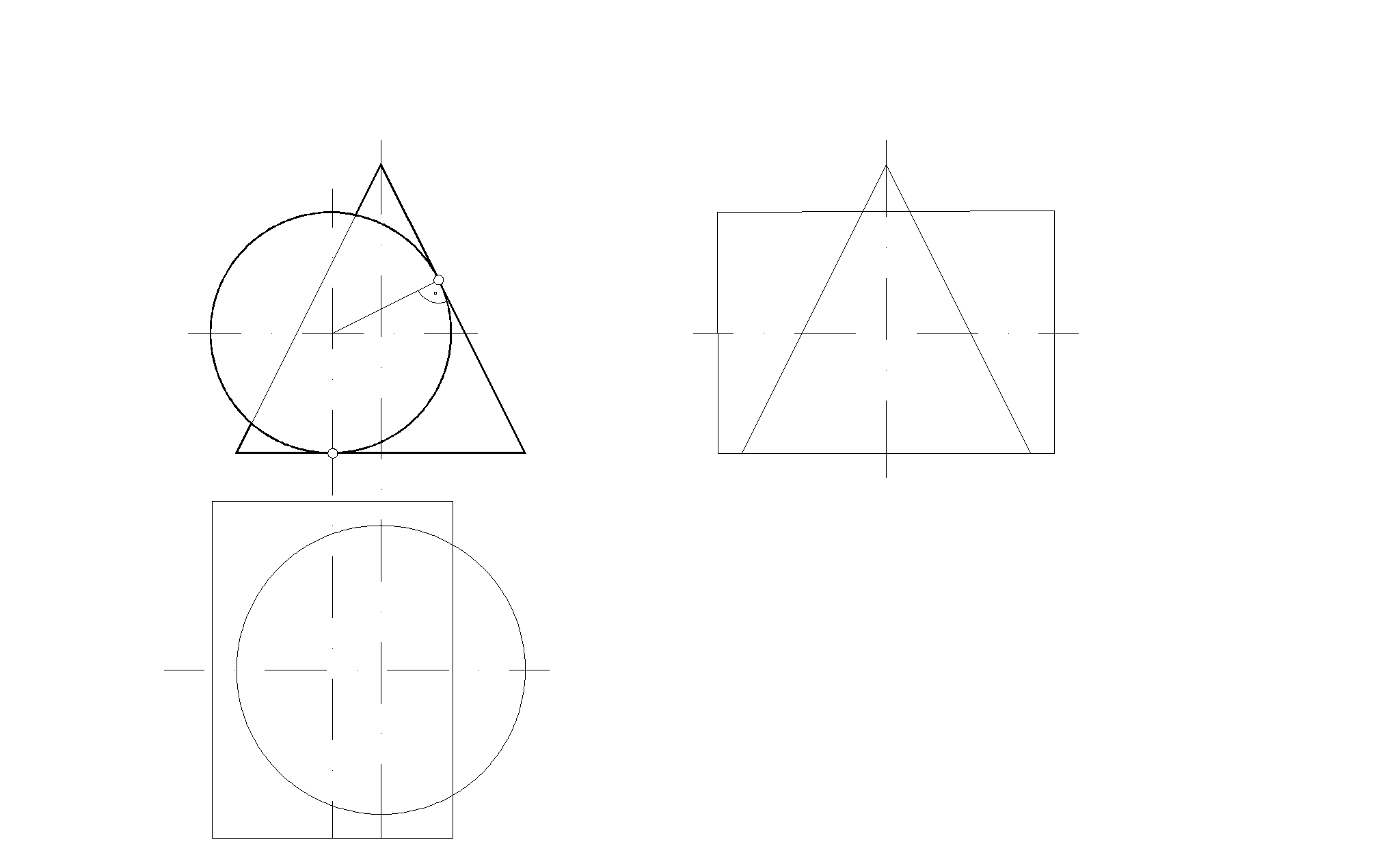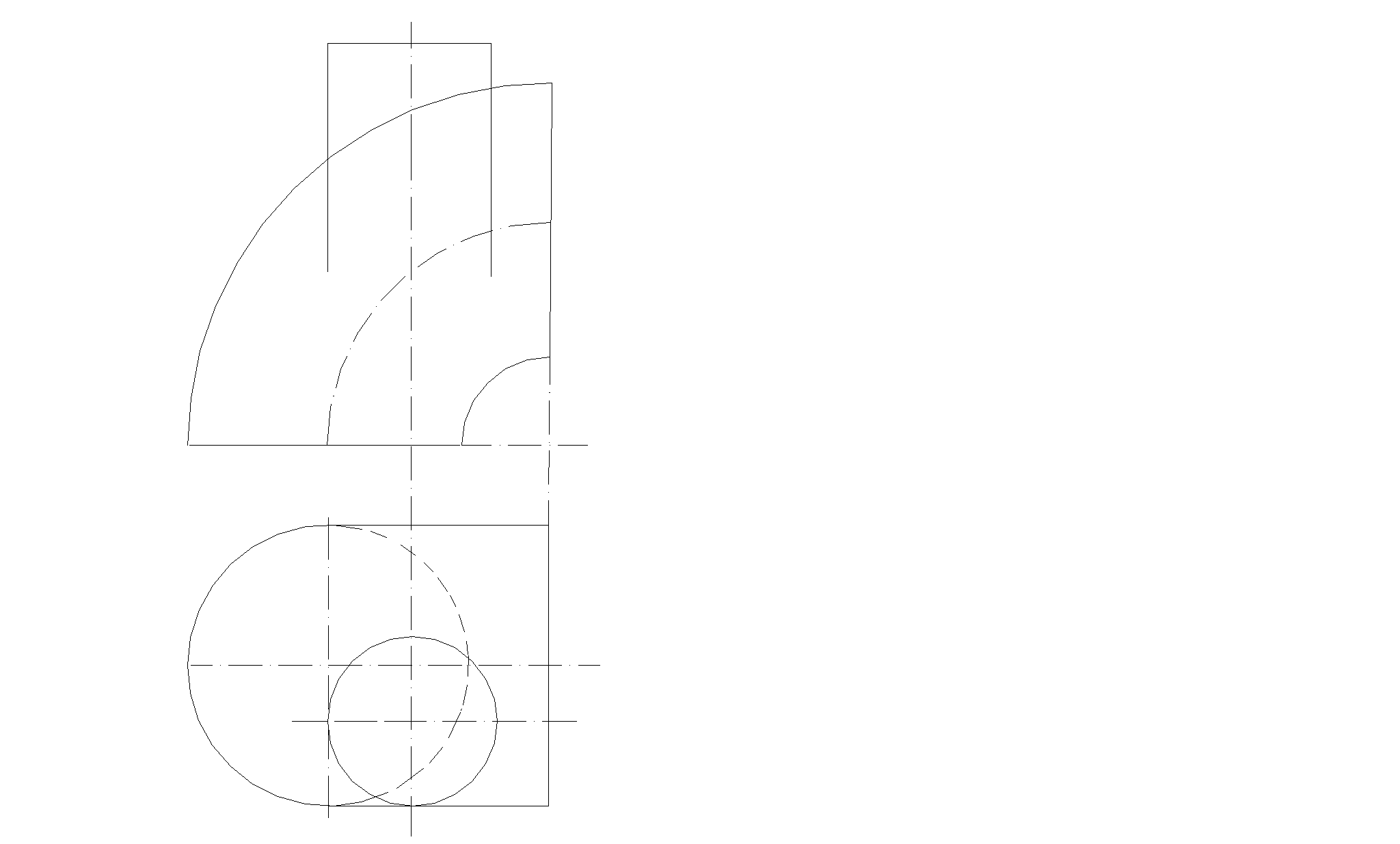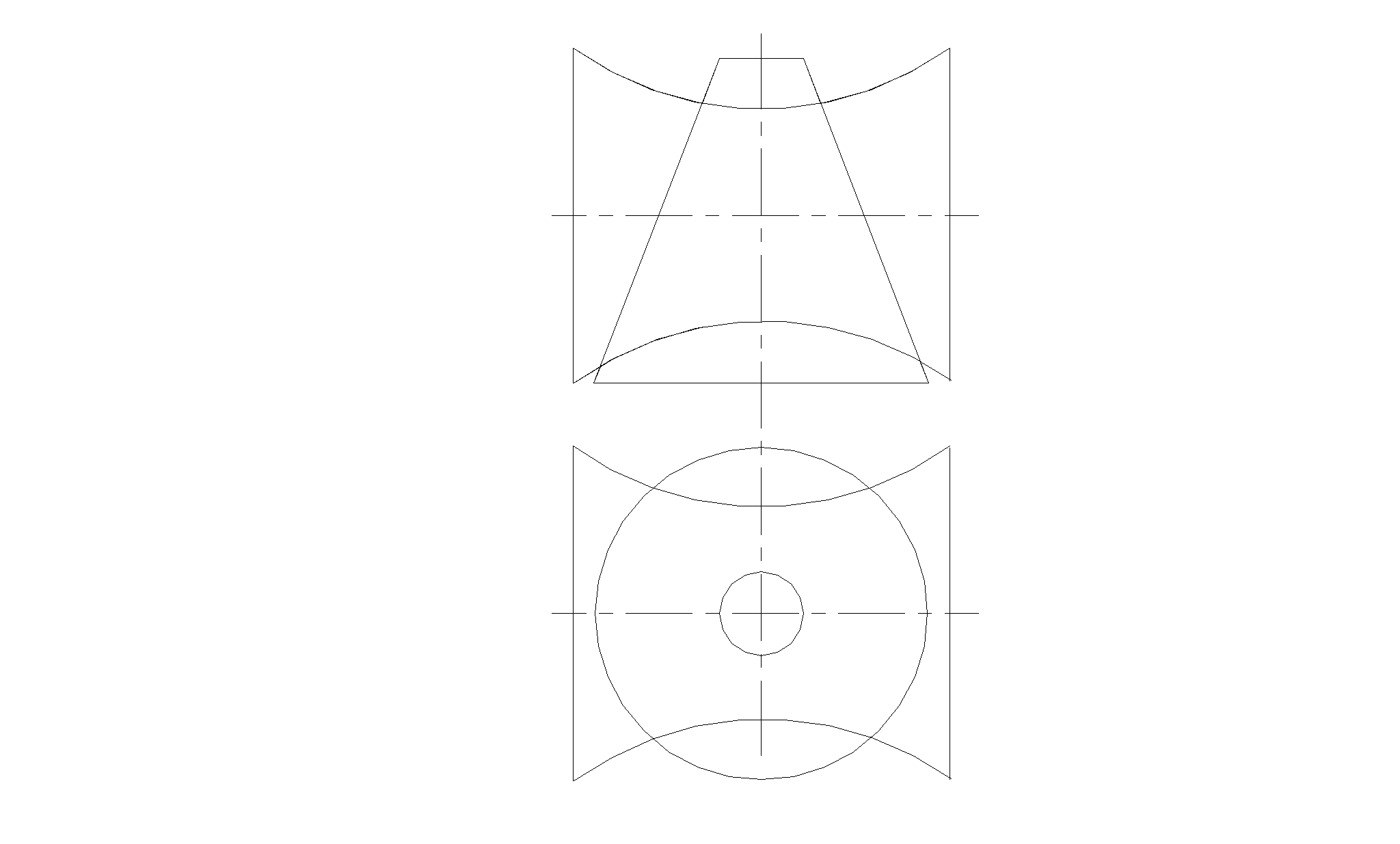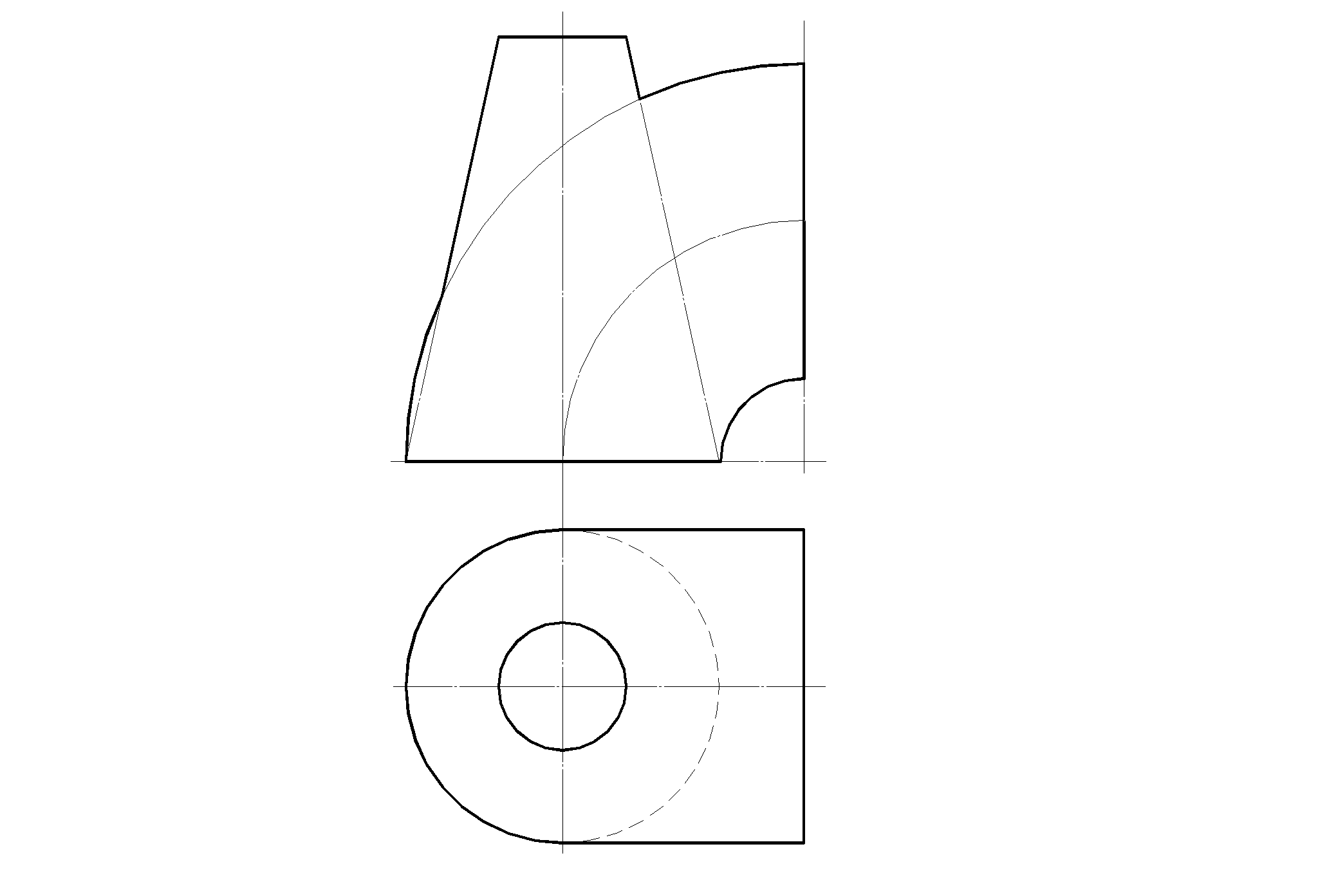|
|
3.1 Начертательная геометрия. Учебное пособие. И. И. Астапкович, Т. В. Борисова
И.И. АСТАПКОВИЧ, Т.В. БОРИСОВА,
М.Н. КУЗЬМИЧЁВА, О.С. МЕЛЬНИКОВА
НАЧЕРТАТЕЛЬНАЯ ГЕОМЕТРИЯ И ИНЖЕНЕРНАЯ ГРАФИКА

КРАСНОЯРСК
2012
Министерство образования и науки Российской Федерации
ФГБОУ ВПО «СИБИРСКИЙ ГОСУДАРСТВЕННЫЙ
ТЕХНОЛОГИЧЕСКИЙ УНИВЕРСИТЕТ»
И.И. Астапкович, Т.В. Борисова, М. Н. Кузьмичёва, О. С. Мельникова
НАЧЕРТАТЕЛЬНАЯ ГЕОМЕТРИЯ И
ИНЖЕНЕРНАЯ ГРАФИКА
Утверждено редакционно-издательским советом СибГТУ
в качестве учебного пособия с примерами решений задач
для практических занятий и самостоятельной работы студентов
по направлению 190100.62 очной формы обучения
Красноярск
2012
Начертательная геометрия и инженерная графика: учебное пособие с примерами решений задач для практических занятий студентов по направлению 190100.62 очной формы обучения / И.И. Астапкович и др. - Красноярск: СибГТУ, 2012. – 56 с.
Применение пособия в учебном процессе позволит сэкономить время, затрачиваемое на переписывание условий и рисунков, исключить возможности искажения условий задач, что способствует повышению эффективности учебного процесса.
Рецензенты: доц. А.В. Михайленко (научно-методический совет СибГТУ)
И. И. Астапкович,
Т. В. Борисова,
М. Н. Кузьмичёва,
О. С. Мельникова
ФГБОУ ВПО «Сибирский государственный технологический университет», 2012
Содержание
Введение 6
Модуль 1 Теоретические основы построения чертежа 8
1 ТОЧКА 8
2 ПРЯМАЯ 11
3 ПЛОСКОСТЬ 16
Модуль 2 Задачи метрические 24
4 ПРЕОБРАЗОВАНИЕ КОМПЛЕКСНОГО ЧЕРТЕЖА 24
Модуль 3 Поверхности и геометрические тела 31
5 МНОГОГРАННИКИ 31
Библиографический список 61
ПРИЛОЖЕНИЕ А 62
ПРИЛОЖЕНИЕ в 64
Введение
Данная методическая разработка предназначена для студентов 1 курса по направлению, 190100.62 очной формы обучения.
Учебное пособие состоит из 7 разделов и включает в себя 80 задач, которые рекомендуются для решения на практических занятиях в процессе изучения курса «Начертательная геометрия и инженерная графика» и для закрепления теоретического материала по темам раздела, а также для самостоятельной работы студентов. Порядок решения задач рассмотрен ниже.
Итогом курса «Начертательная геометрия и инженерная графика» является дифференцированный зачет и экзамен. Составной частью зачета является решение всех задач, включенных в этот сборник, и умение объяснить решение любой задачи. Успешное освоение практических занятий позволяет сформировать у бакалавров направления 190100.62 «Наземные транспортно – технологические комплексы» профилей подготовки: «Машины и оборудование природообустройства и защиты окружающей среды»; «Машины и оборудование для садово-паркового ландшафтного строительства» следующие общекультурные и профессиональные компетенции:
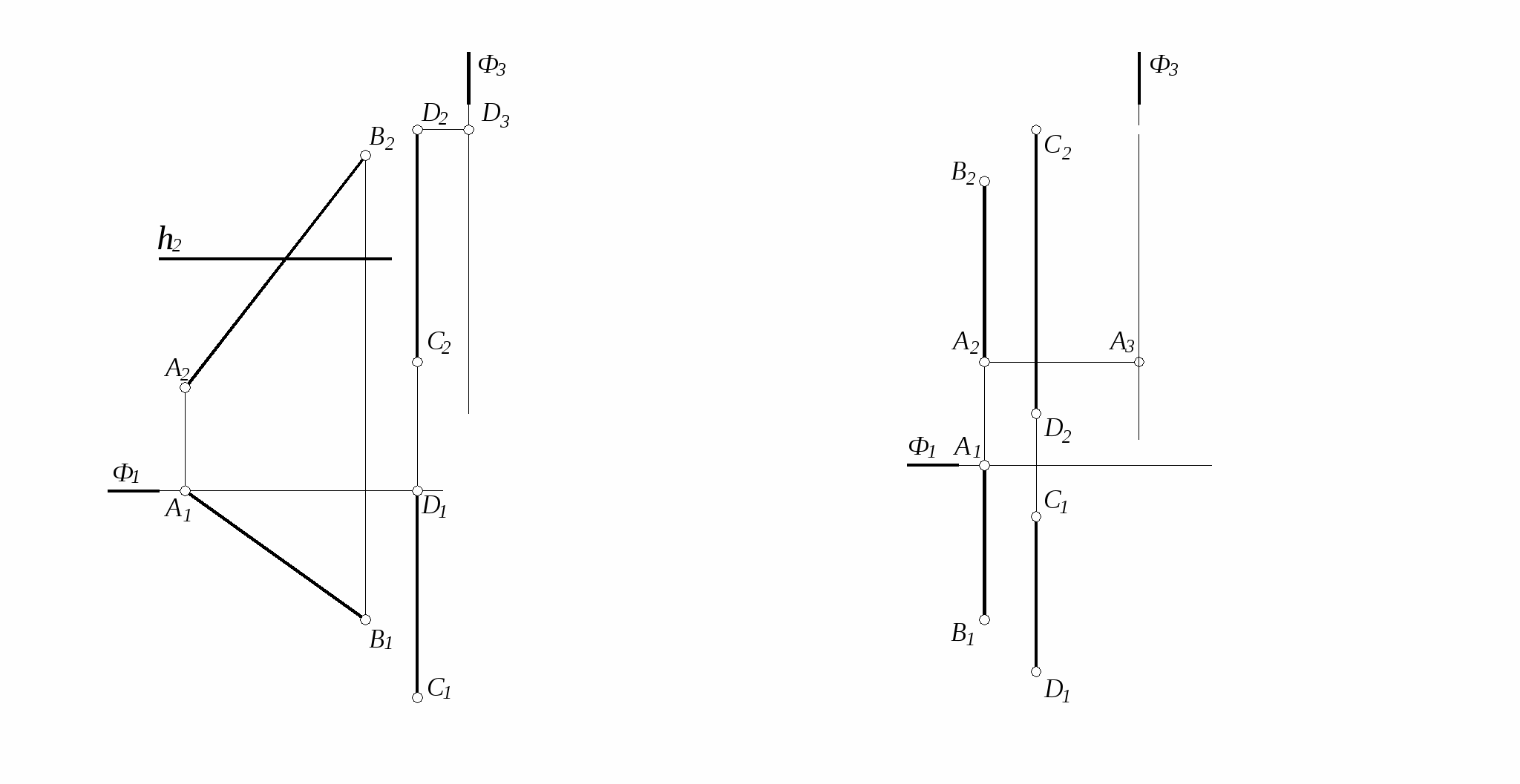
ОК – 1: владеет культурой мышления, способен к обобщению, анализу, восприятию информации, постановке цели и выбору путей ее достижения;
ПК – 8: способен в составе коллектива исполнителей участвовать в разработке конструкторско-технической документации новых или модернизируемых образцов наземных транспортно-технологических машин и комплексов.
Порядок решения задач
1. Восстановить в памяти лекционный материал по конспекту лекции и проработать его по указанной ниже литературе.
2. Ответить на вопросы для самопроверки по разделу.
3. Внимательно изучить условие задачи и мысленно представить расположение в пространстве геометрических элементов, о которых говорится в условии.
4. Составить план решения задачи в пространстве, выполнить символическую запись, а затем выполнить решение на комплексном чертеже (эпюре).
5. Если затруднительно мысленно представить ход решения задачи в пространстве, то можно выполнить от руки аксонометрический эскиз или сделать модель, используя подручные материалы (булавки, спички, обрезки проволоки, куски картона и т.п.).
6. Задачи следует решать непосредственно в рабочей тетради карандашом, с применением чертежных инструментов, добиваясь максимальной точности. Рекомендуется также применять цветные карандаши.
7. Задачи необходимо решать систематически в течение семестра в соответствии с рекомендациями преподавателя.
Модуль 1 Теоретические основы построения чертежа 1 ТОЧКА
1.1 Задачи к разделу 1
В чем заключается сущность метода проекций?
Что называется осью проекций?
Какое различие между проекциями:
центральными и параллельными?
косоугольными и прямоугольными?
Что называется комплексным чертежом?
Какие координаты определяют положение горизонтальной, фронтальной и профильной проекции точки относительно начала координат?
Какие координаты дают информацию о широте, глубине и высоте точки?
Какие точки называются конкурирующими?
_____________________________________________________________
1. Построить недостающие проекции точек на наглядном изображении и их комплексный чертеж. Как расположены точки относительно плоскостей проекций? Как расположены точки относительно точки А?
Записать координаты точек.
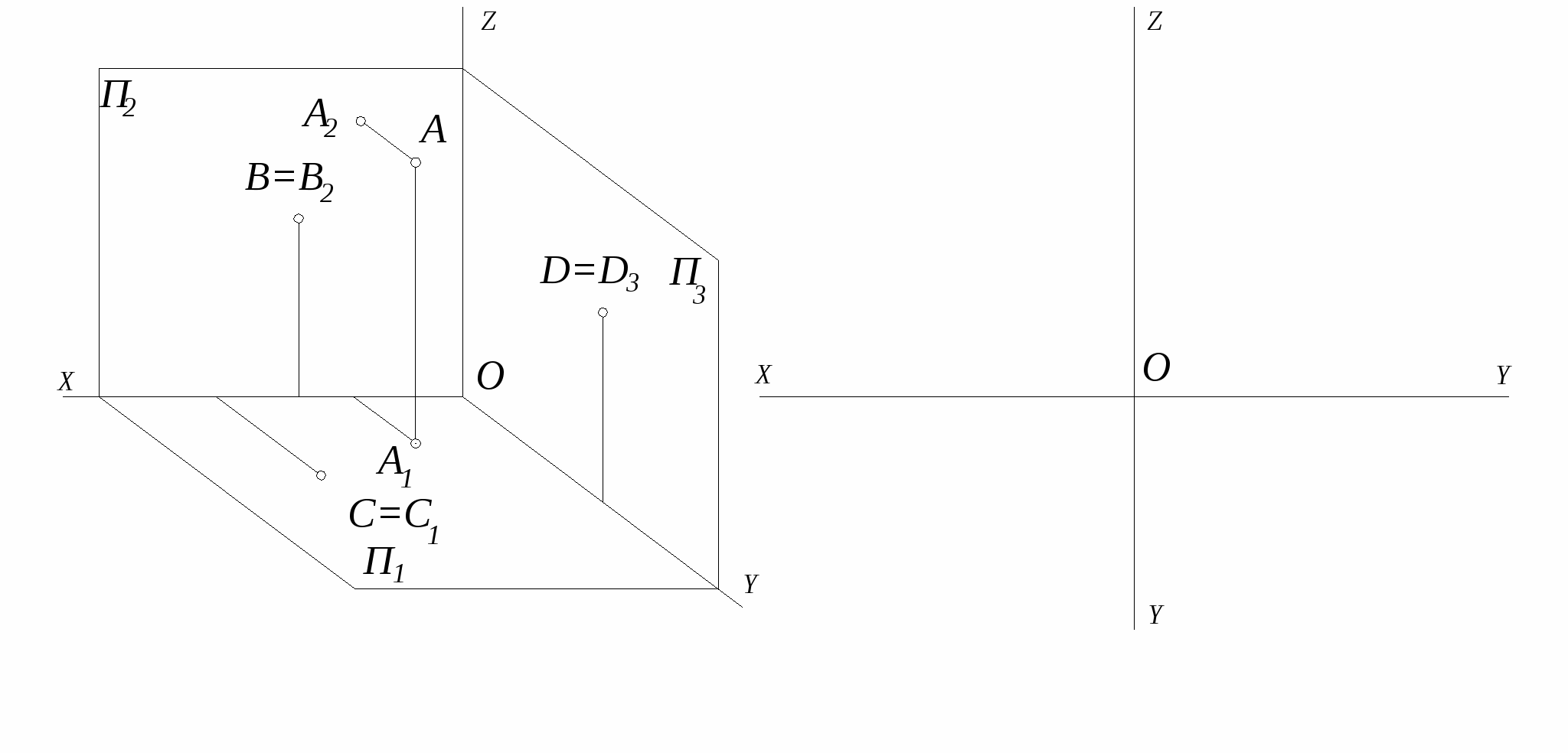
1 Точка А__________________ 2 Точка В (А)__________________
Точка В___________________ Точка С (А)__________________
Точка С___________________ Точка D (А)__________________
Точка D__________________
3 (.) А ( ____________________ ) (.) В ( ____________________ )
(.) С ( ____________________ ) (.) D ( _____________________ )
2. Построить три проекции точек по координатам.
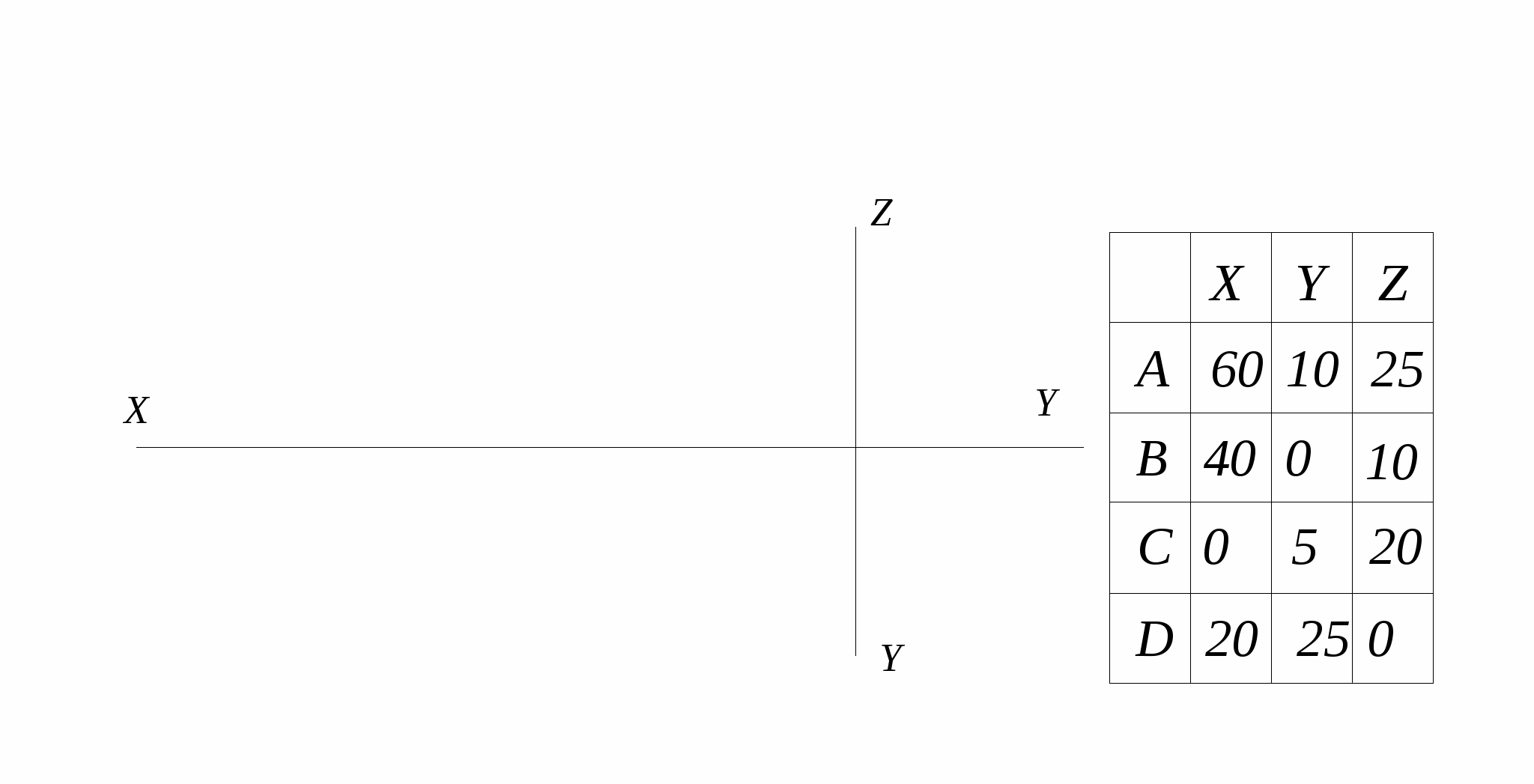 3. Относительно базовой точки А построить проекции точек: 3. Относительно базовой точки А построить проекции точек:
(.) В(А) – выше на 10 мм (.) С(А) – дальше на 15 мм
(.) D(A) – правее на 40 мм (.) Е(А) – левее на 20 мм и ниже на 10 мм
(.) F(А) – правее на 40 мм, выше на 10 мм, ближе на 10 мм.
4. Построить недостающие проекции по двум заданным
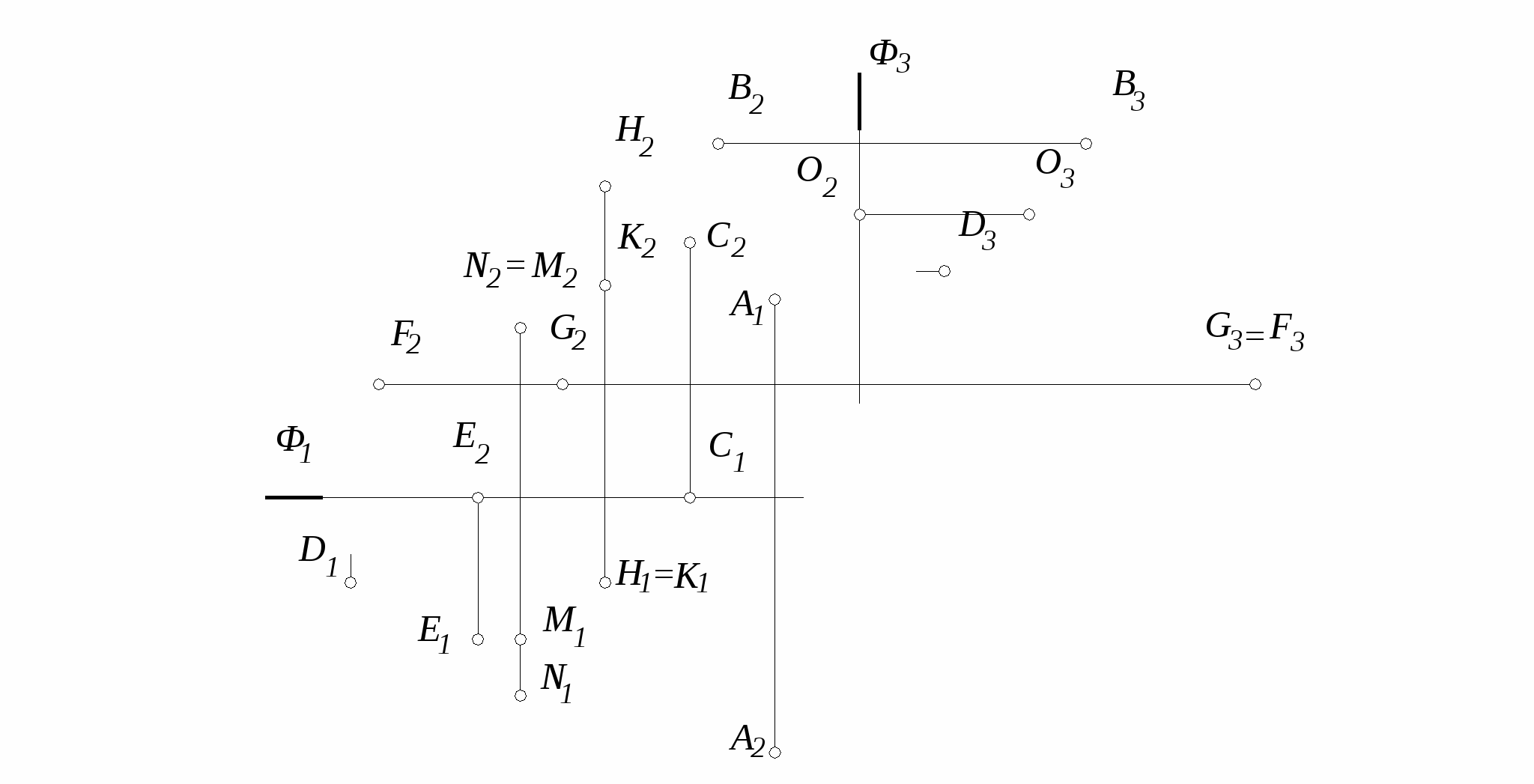
1.2 Примеры решения задач раздела 1
1. Построить недостающие проекции точек на комплексном чертеже и их наглядное изображение. Как расположены точки относительно плоскостей роекций?
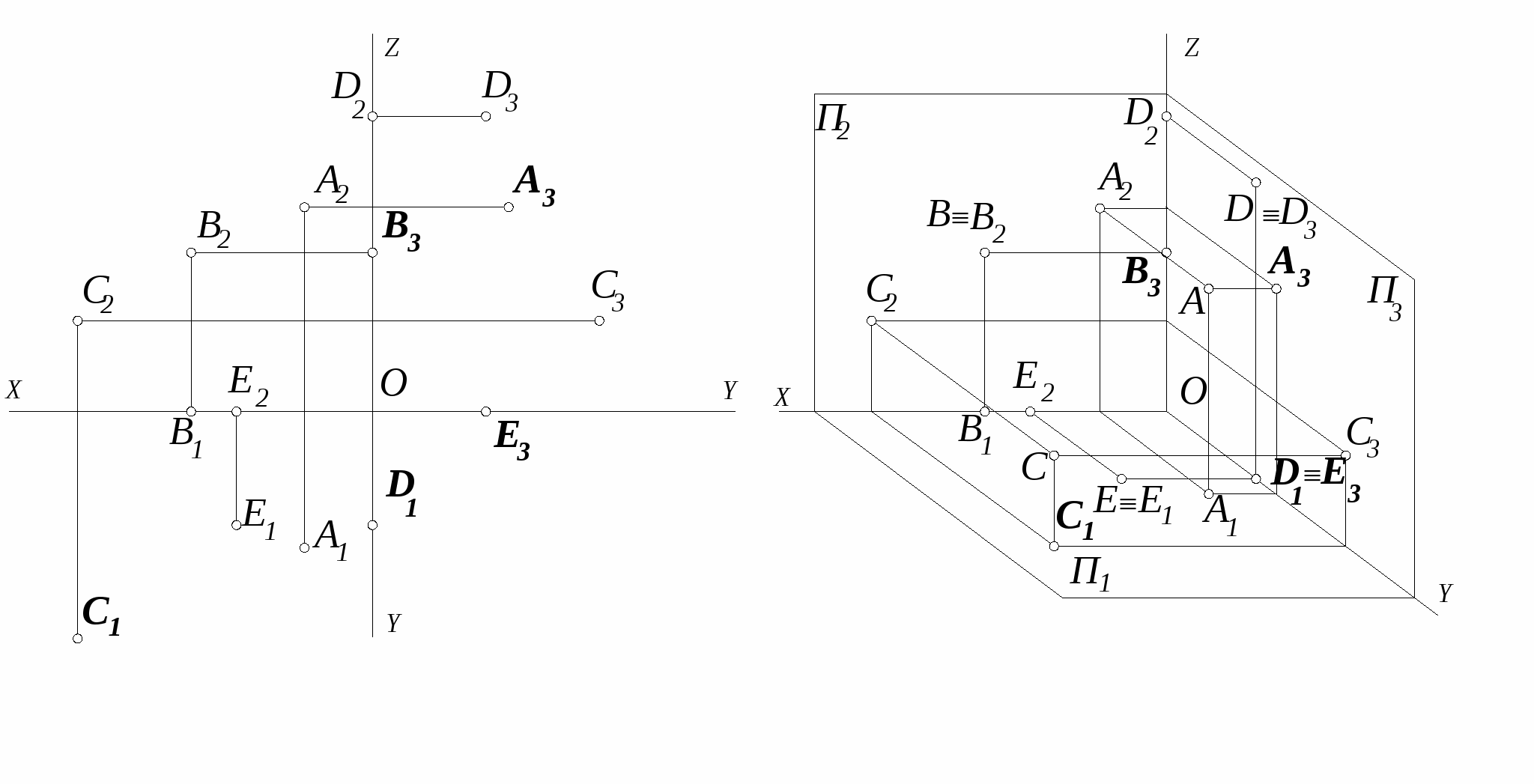
(.) А П1, П2, П3
(.) В П2
(.) С П1, П2, П3
(.) D П3
(.) E П1
2
D2
F1
E1
K1
F2
E2
K2
.Выяснить взаимное положение точек B, C, D, E, F,G, H, K
относительно точки А
H1
D1
G2
G1
C1
B2
 В (А) – выше; В (А) – выше;
А2С2
С (А) – ближе;
D (А) – левее;
H2
Е (А) – правее;
F (А) – ближе, правее;
G (А) – выше, левее;
H (А) – правее, ниже, дальше;
K (А) – правее, выше, ближе;
A1B1
2 ПРЯМАЯ
2.1 Задачи к разделу 2
Что является проекцией прямой в общем случае? В частном случае?
Дать определение прямой общего положения. Каково соотношение между отрезком прямой общего положения и его проекцией?
Дать определение прямых уровня.
Какие особенности присущи проекциям прямых уровня?
Дать определение проецирующих прямых.
Какие особенности присущи проекциям проецирующих прямых?
Всегда ли проецирующая прямая является прямой уровня?
Как на комплексном чертеже определить принадлежит ли точка прямой?
Как разделить отрезок на комплексном чертеже?
______________________________________________________________
5. Построить три проекции отрезков АВ и CD по координатам.
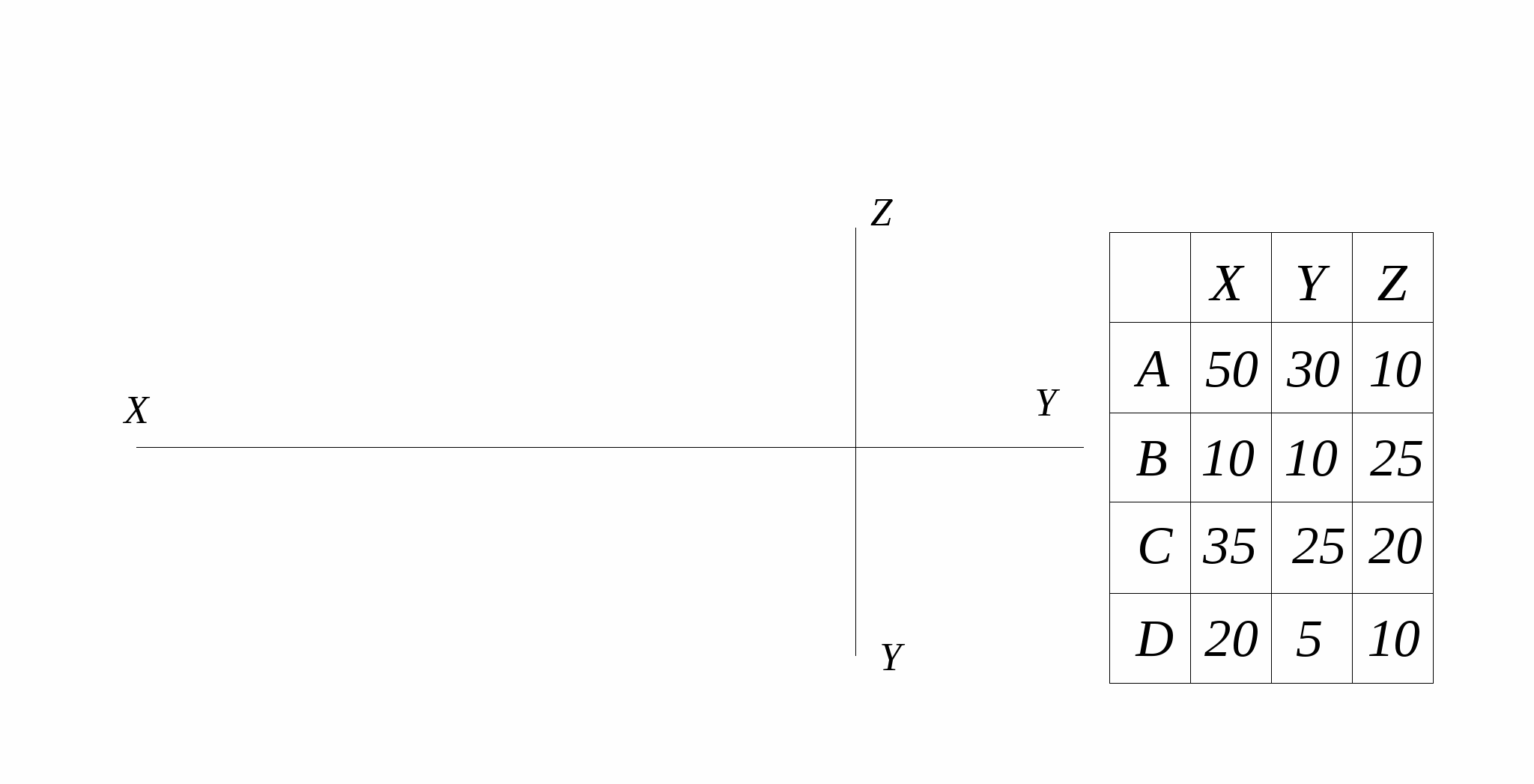
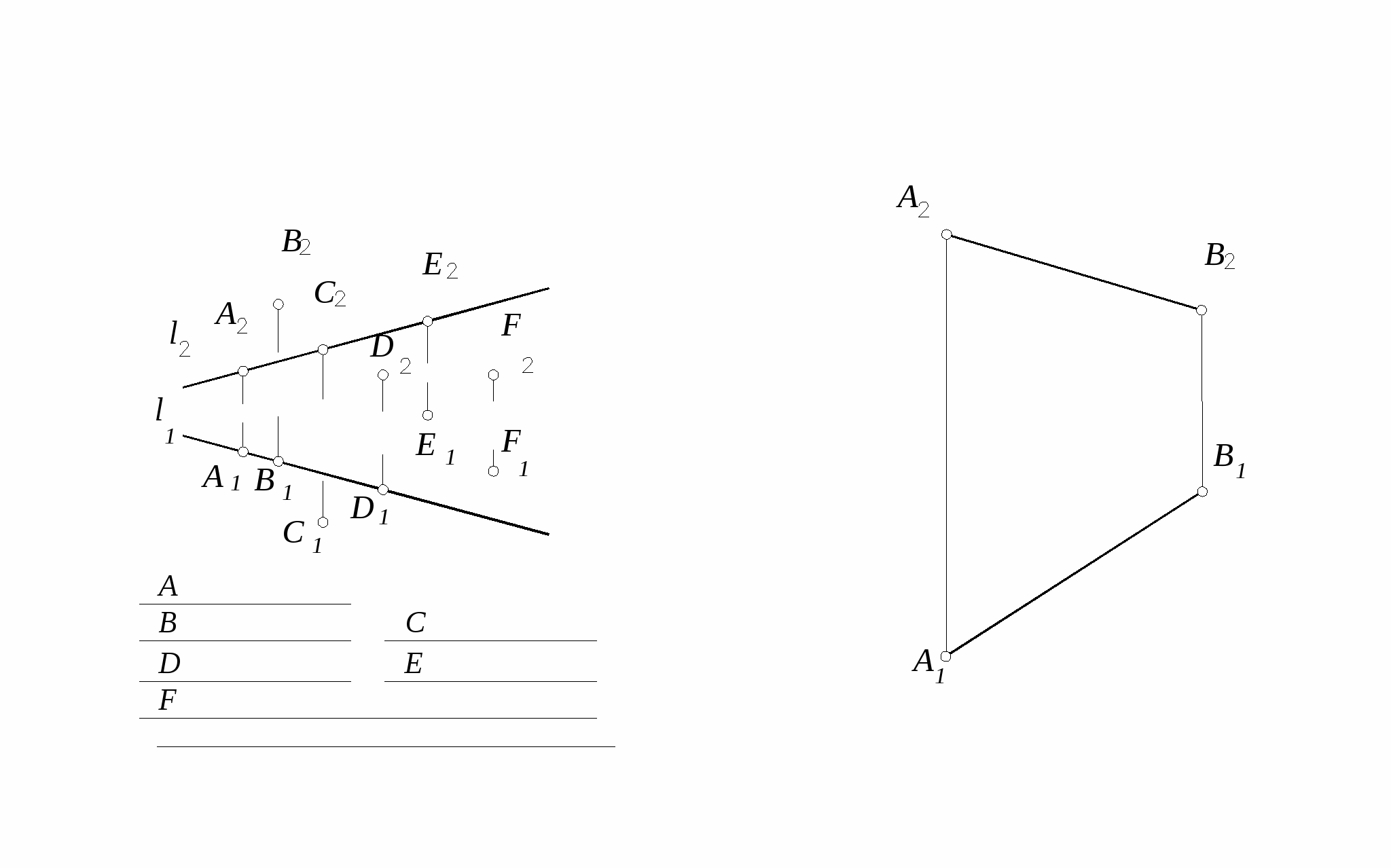
6. Записать как расположены 7. Разделить отрезок прямой АВ
точки A, B, C, D, Е, F точкой С в отношении АС:СВ=3:2.
относительно прямой l.
8. Построить проекции отрезков:
а) АВ // П1; /АВ/ = 30 мм; б) CD // П2; /CD/ = 40 мм;
АВ ^ П2 = 45 CD ^ П1 = 30

_____________________________________________________________
в) EF // П3; /EF/ = 20 мм; г) KL П2; /KL/ = 25 мм:
EF ^ П1 =45

________________________________________________________________
д) MN П1; /MN/ = 30 мм е) KH П3; /KH/ = 30 мм

9. Определить взаимное расположение прямых.
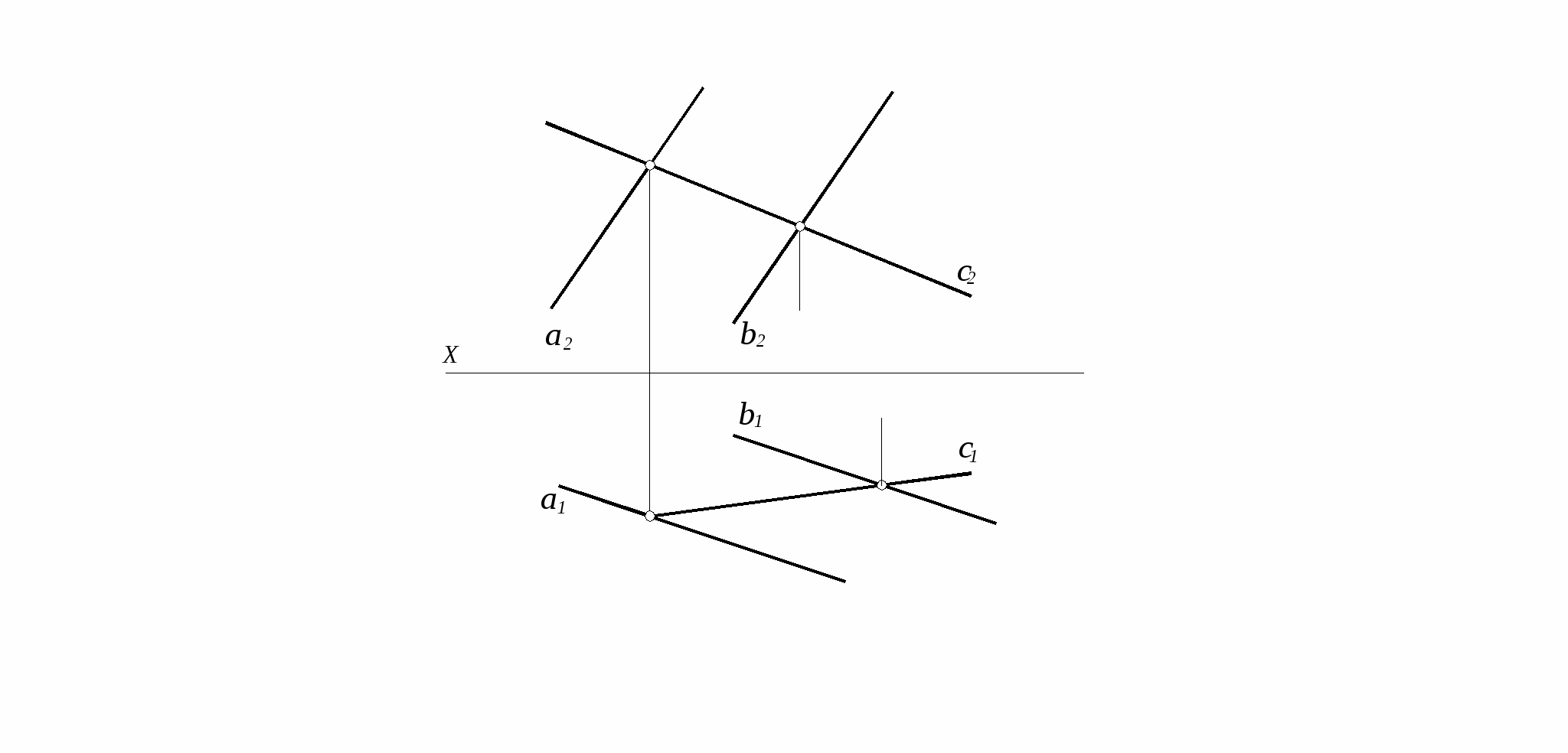
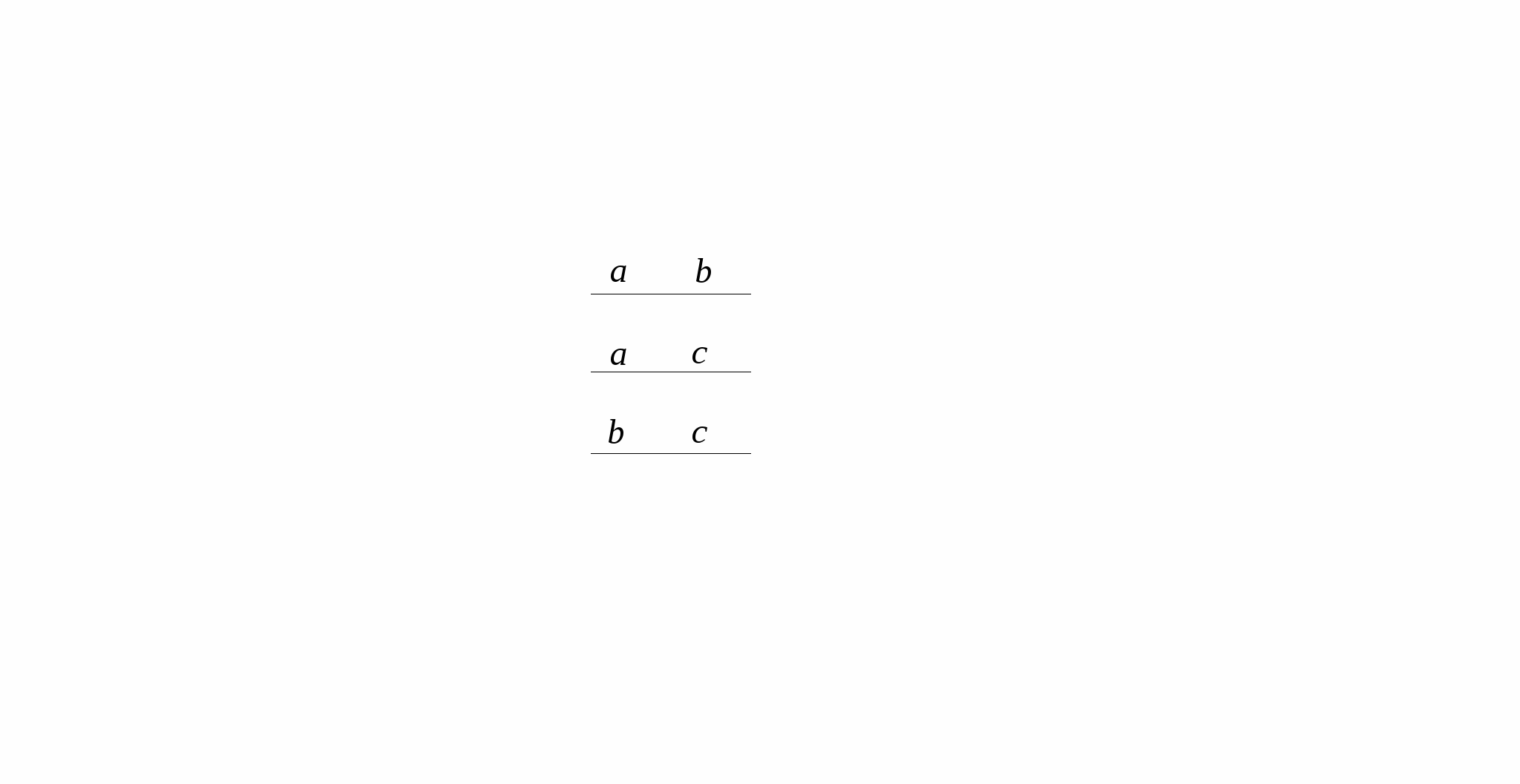
10. Определить видимость ребер пирамиды. Записать название конкурирующих точек.

________________________________________________
_________________________________________________
_________________________________________________
11. Провести через точку А 12. Провести прямую n,
прямую l, пересекающую параллельную прямой m
прямые ВС и DE. и пересекающую прямую l.
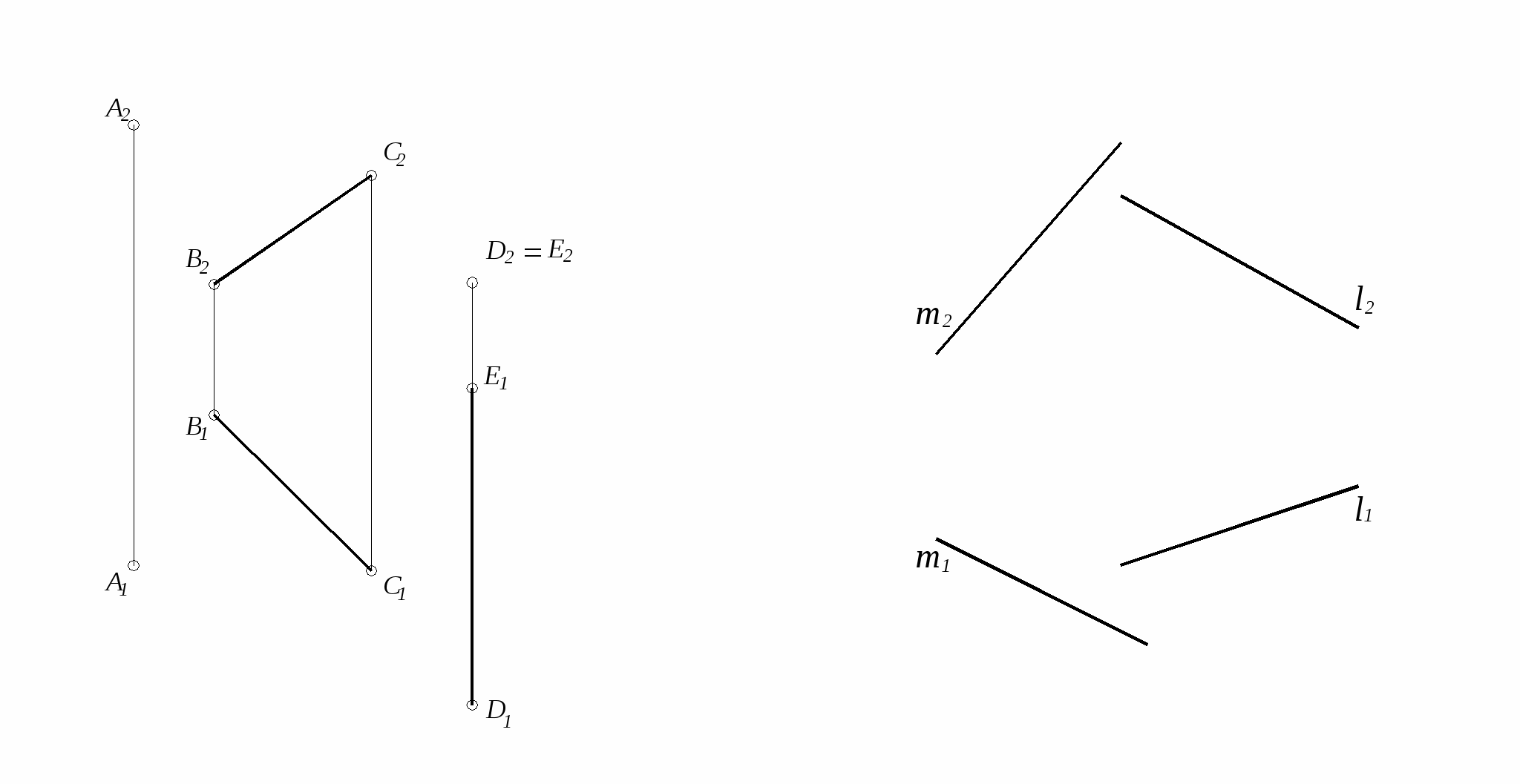
13.Построить горизонтальную 14. Выяснить взаимное
проекцию h 1 прямой h, положение прямых AB и CD.
пересекающую прямые АB и CD.
AB CD
2.2 Примеры решения задач раздела 2
А2
В2
А1
Н.В.
Н.В.
а)
б)
1.Построить проекции отрезка прямой линии длиной 40 мм:
а) параллельного горизонтальной б) перпендикулярного фронтальной
плоскости проекций; плоскости проекций.

В1
(С2)D2
C1
D1
2.Пересечь прямые AB и CD горизонтальной прямой уровня
C2
А2
А1
В2
В1
C1
D2
D1
12
11
22
21
h2
h1
3 ПЛОСКОСТЬ
3.1 Задачи к разделу 3
Какими геометрическими элементами можно задать плоскость общего положения на комплексном чертеже?
Дать определение плоскости:
общего положения
уровня
проецирующей
Сформулировать признаки:
принадлежности прямой плоскости
параллельности прямой и плоскости
принадлежности точки плоскости
Перечислить прямые особого положения в плоскости .
Как расположены относительно плоскостей проекций прямые уровня в проецирующих плоскостях?
Как определить угол наклона плоскости к плоскостям проекций?
_____________________________________________________________
15. Построить три проекции плоскости, заданной координатами четырех ее точек: A, B, C, D.

16. Заключить прямые:
l в горизонтально проецирующую плоскость,
t – во фронтально проецирующую плоскость
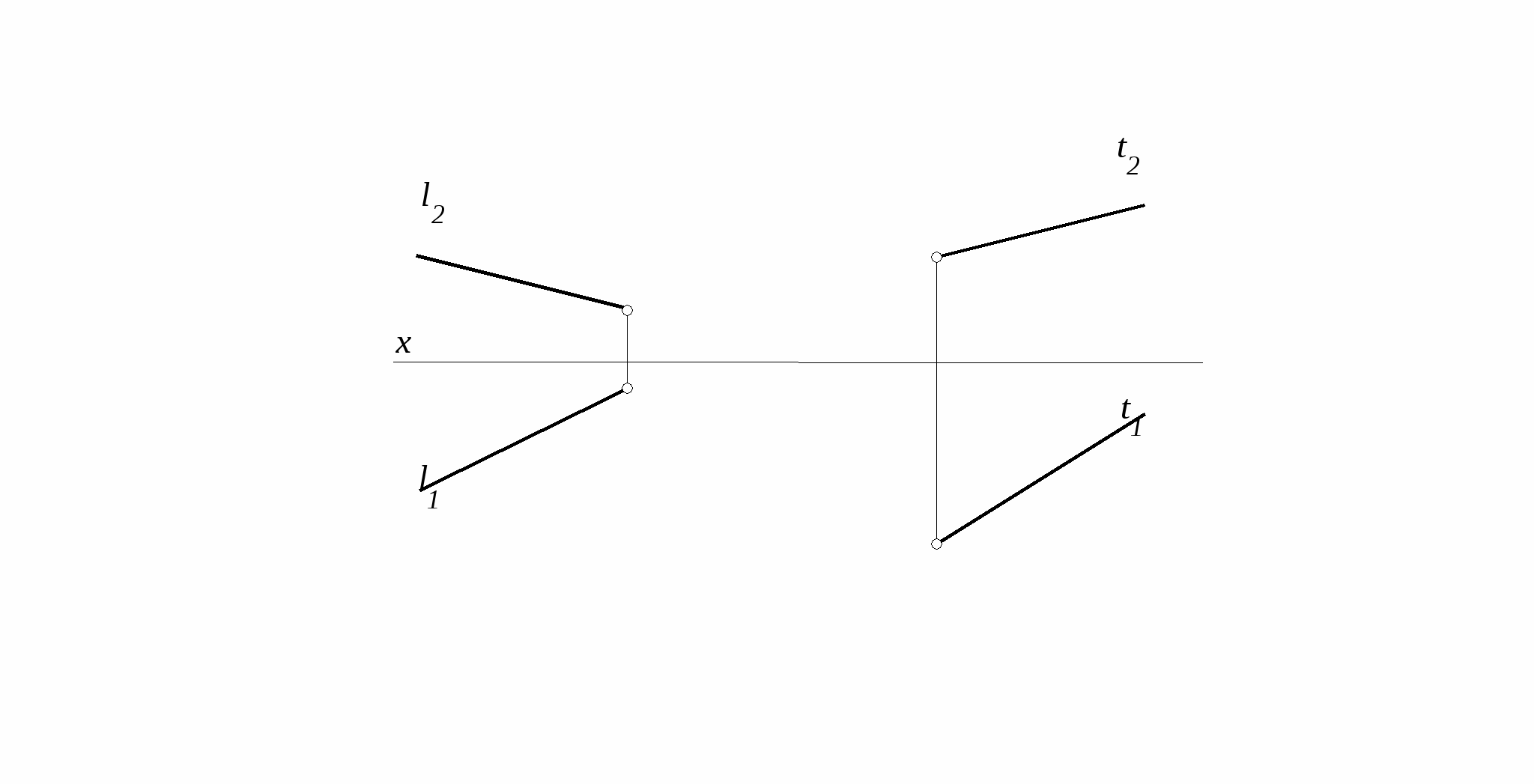
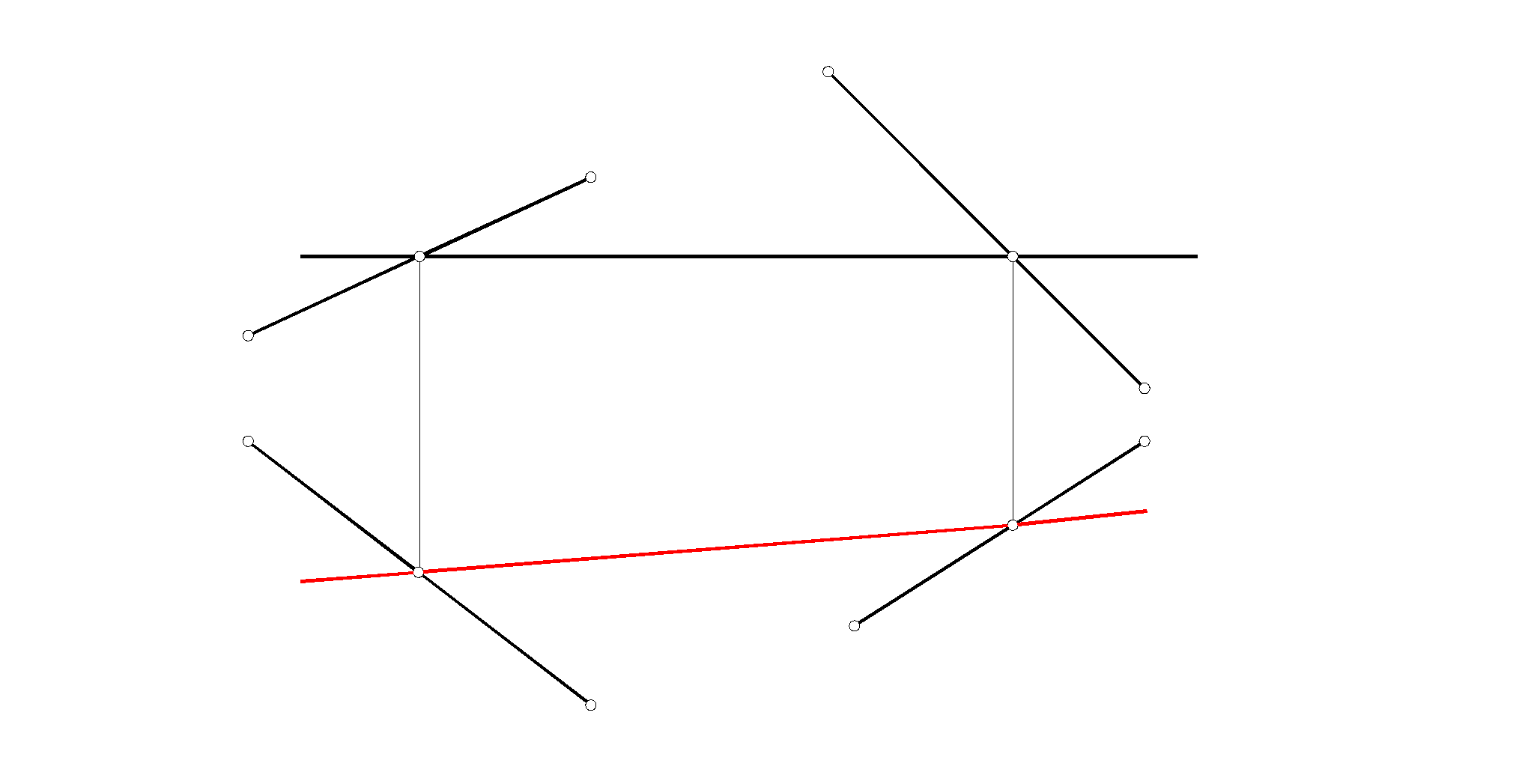
17. По комплексным чертежам определить, как расположены заданные плоскости относительно плоскостей проекций. Записать в таблицу символически. Записать названия этих плоскостей.
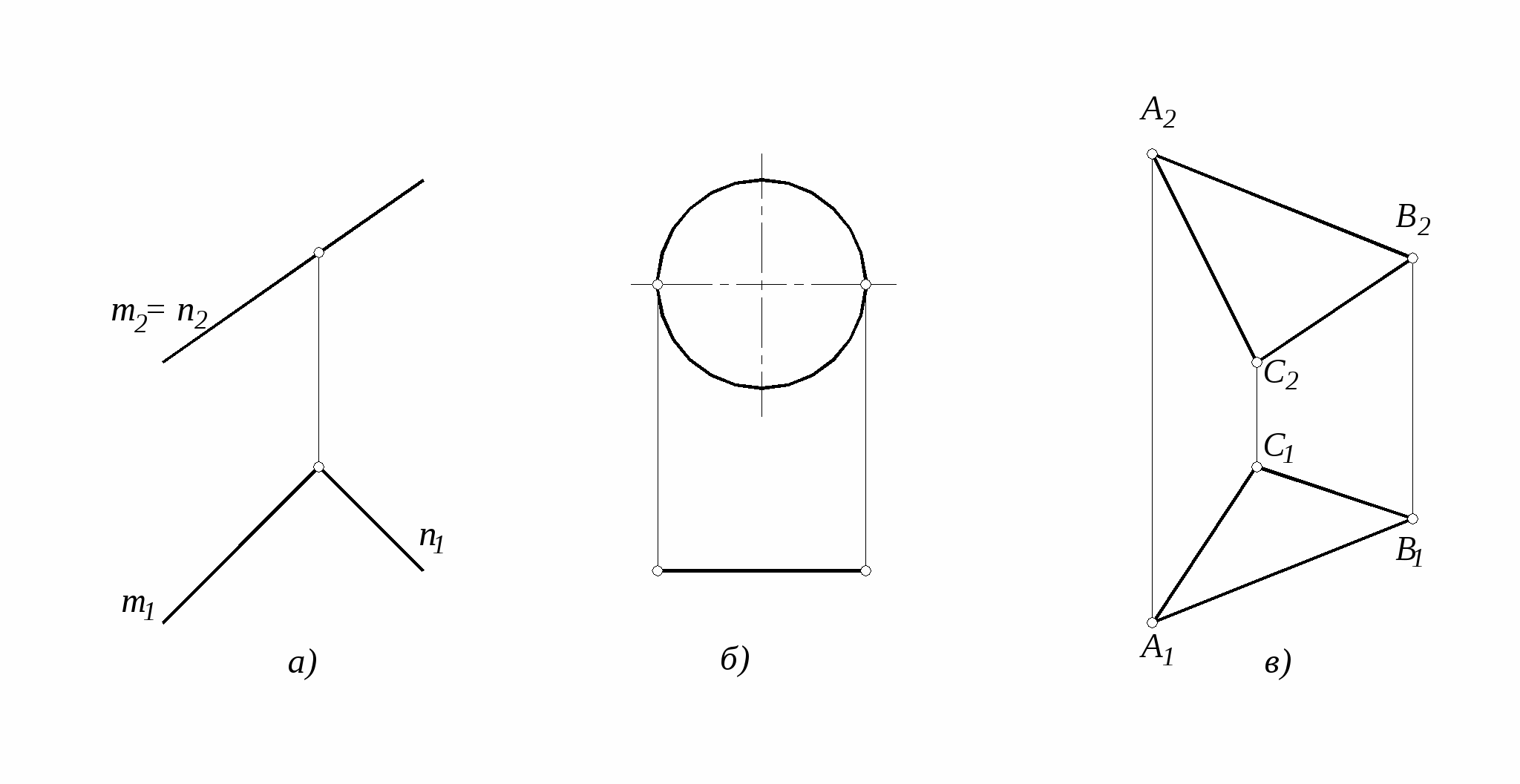
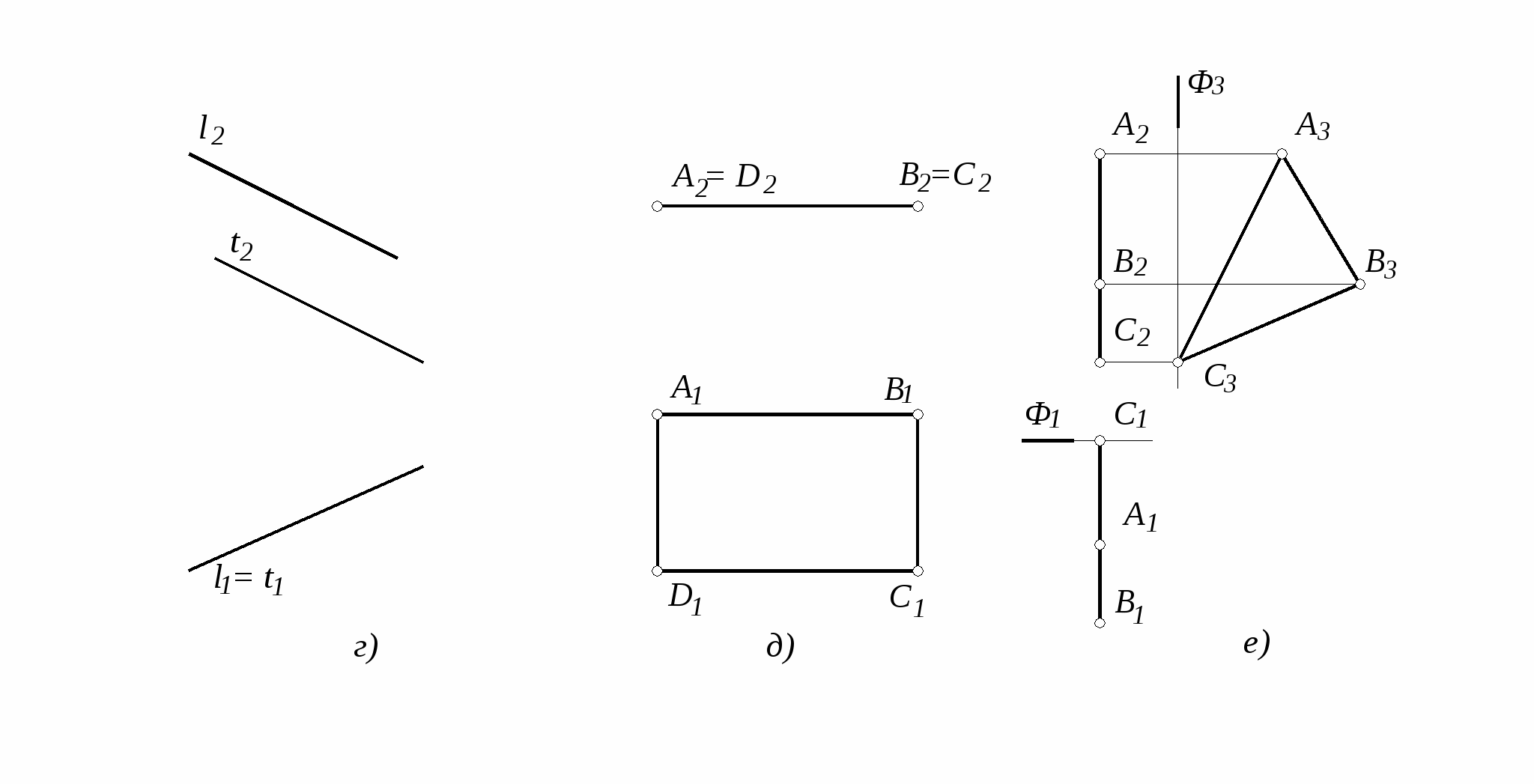 
18. Найти недостающие 19. Построить фронтальную
проекции точек М и К. проекцию прямой l, принадлежащей
плоскости Q (а // в).
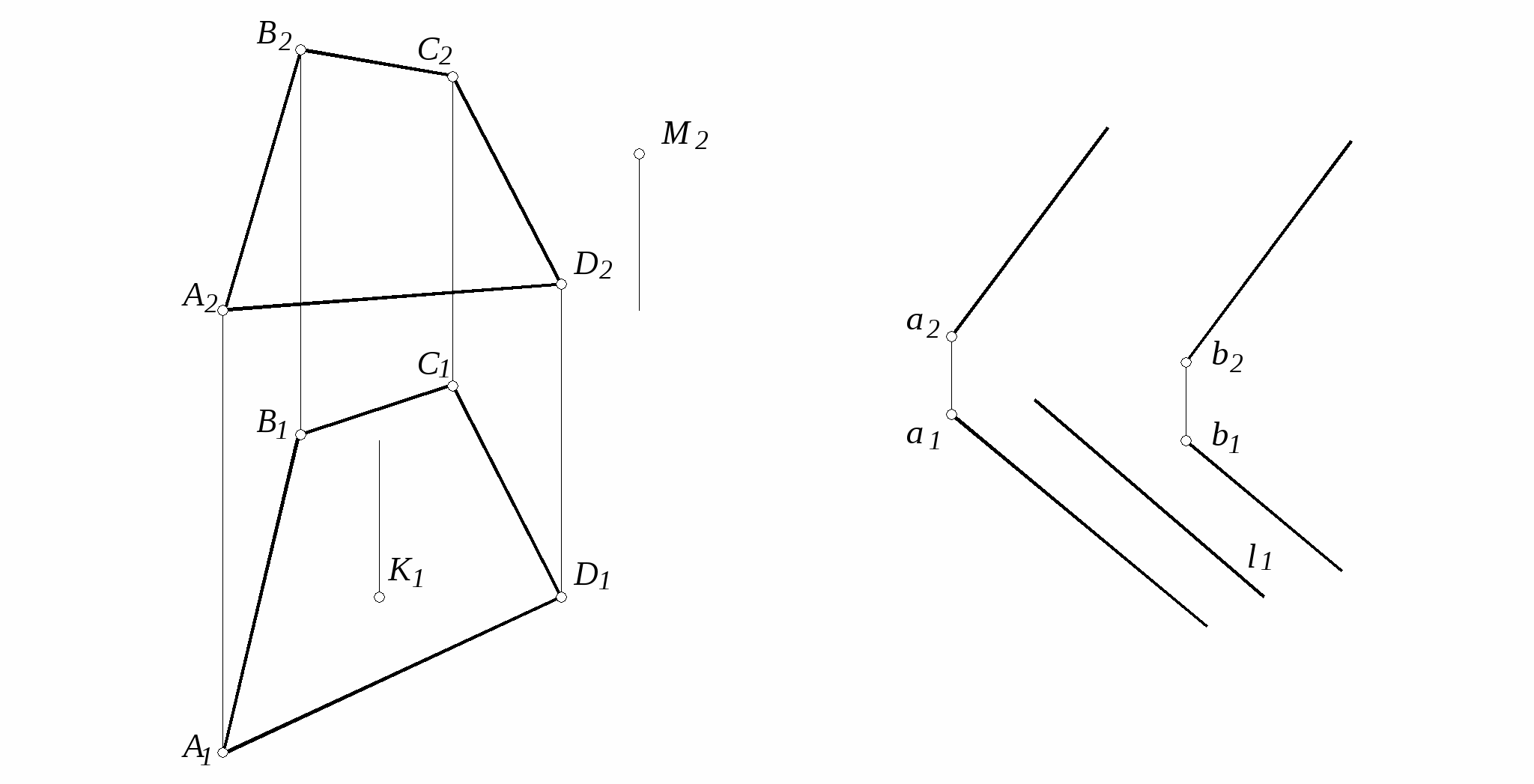
20. В плоскости АВС 21. Достроить фронтальную
построить линии уровня ( h, f, p ). проекцию пятиугольника ABCDE.
Записать натуральнyю величину:
h = _______ f = _______ p = _______
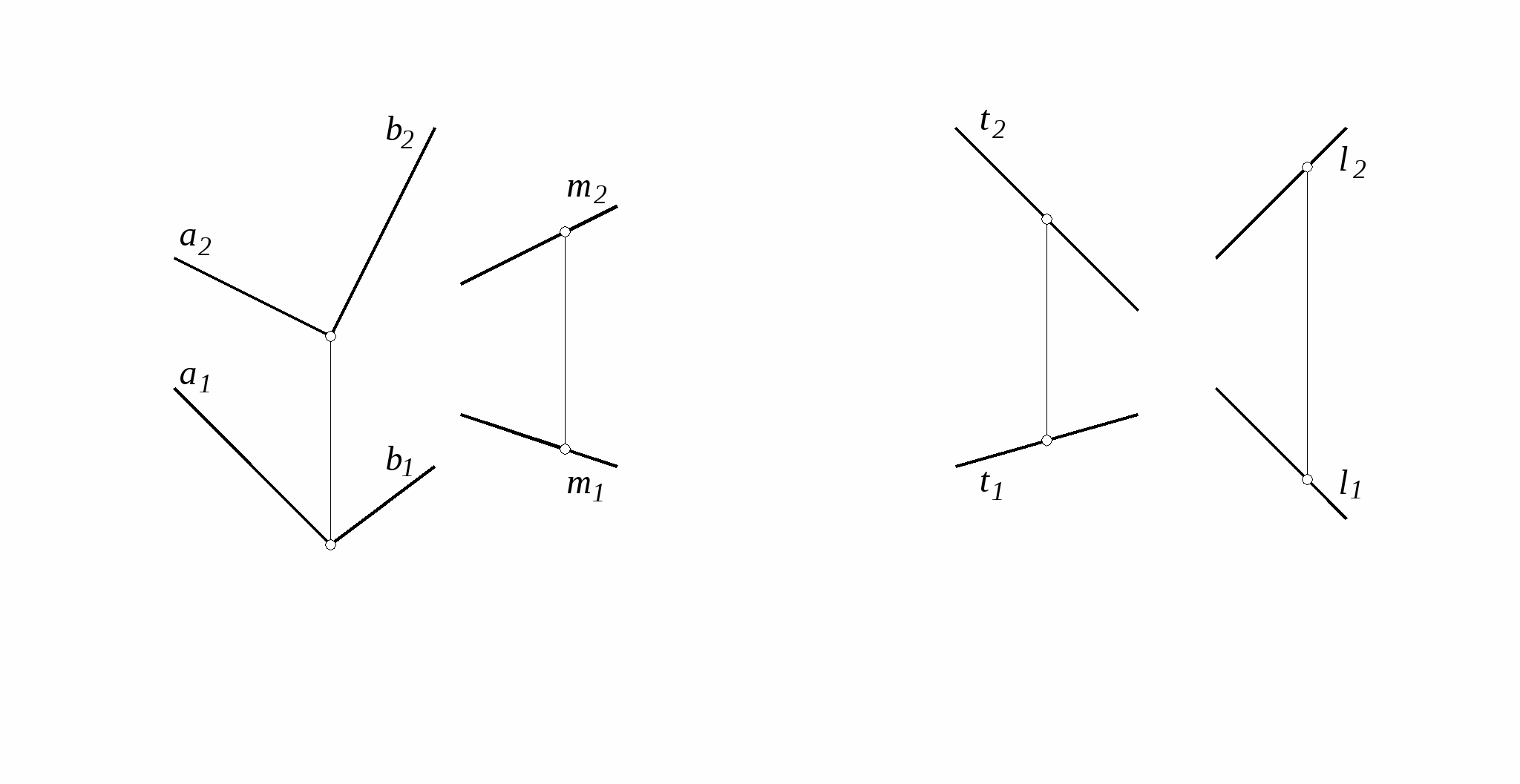
22. Определить, параллельны 23. Через прямую t провести
ли прямая m и плоскость плоскость Q, параллельную
Q (a ∩ b). прямой l.
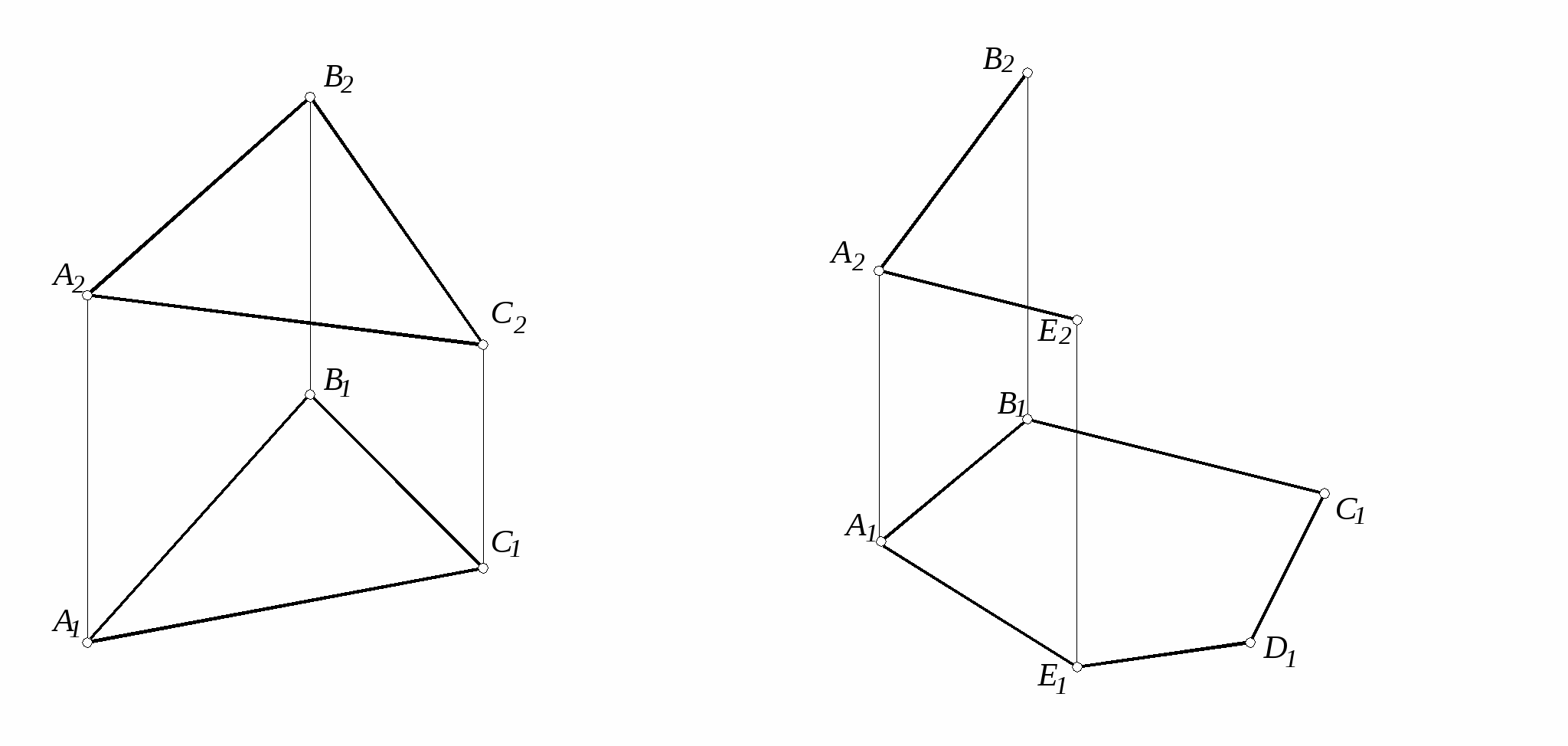
24. Определить, параллельны 25. Провести через точку А
ли данные плоскости плоскость параллельную
T ( DEF ) и G ( h f ). плоскости Q ( m // l ).
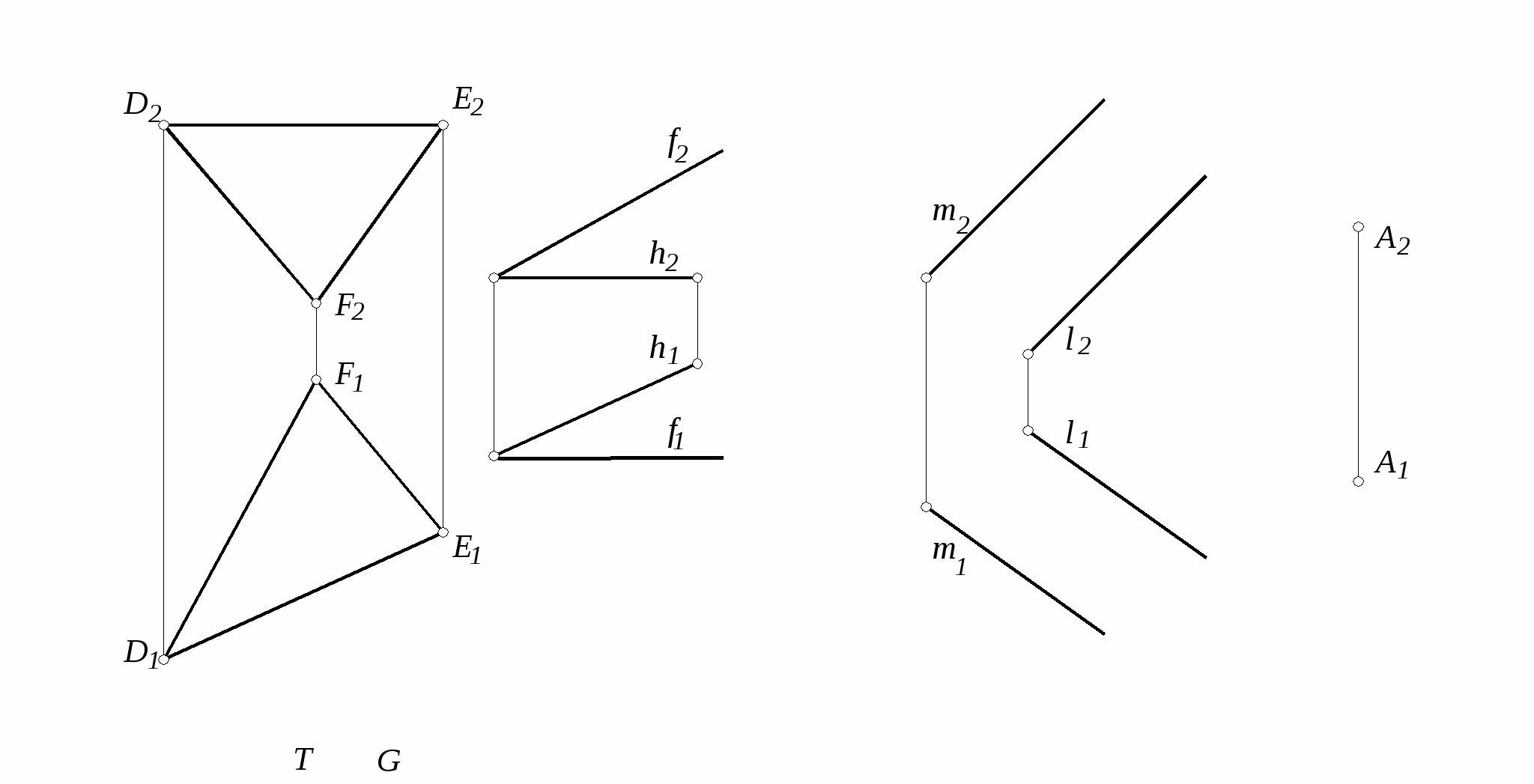
26. Построить проекции точки пересечения прямой l с плоскостями и
определить видимость ее относительно плоскости.
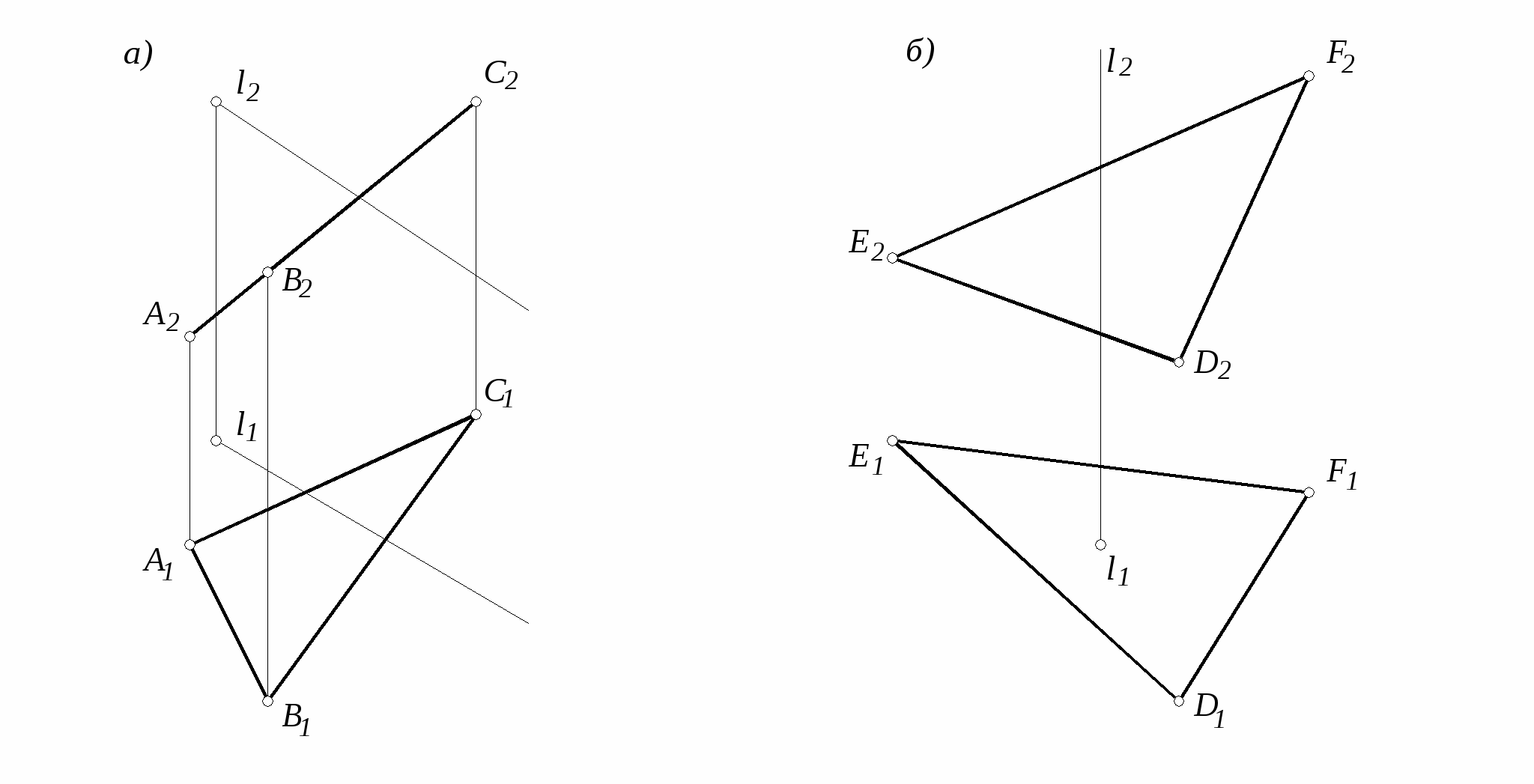
27. Построить линию пересечения
плоскостей. Определить видимость
элементов.
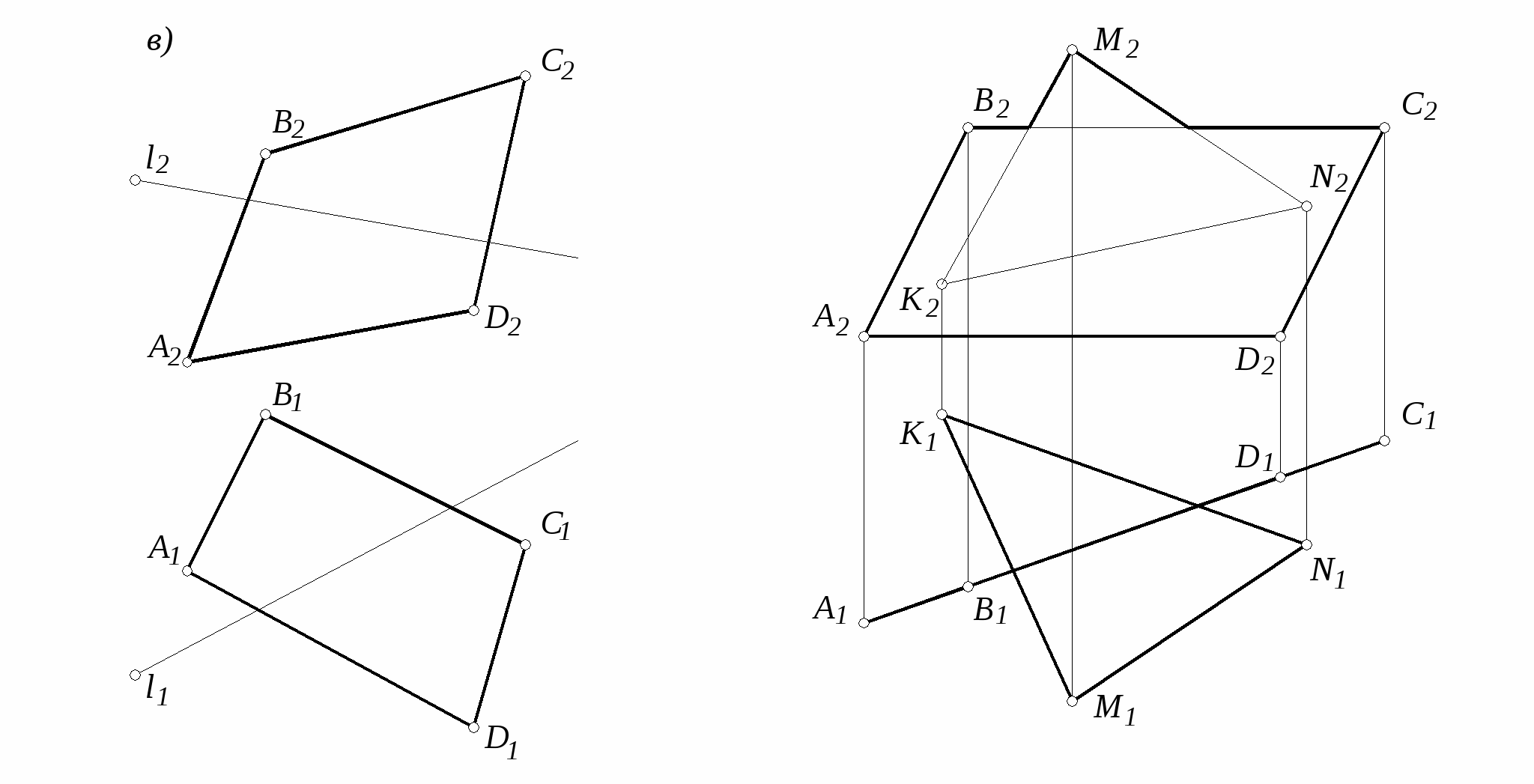
28. Построить линию пересечения треугольников АВС и KMN. Определить видимость треугольников в проекциях.
3.2 Примеры решения задач раздела 3
О
А1
12
11
22
21
n2
m1
n1
m1
21
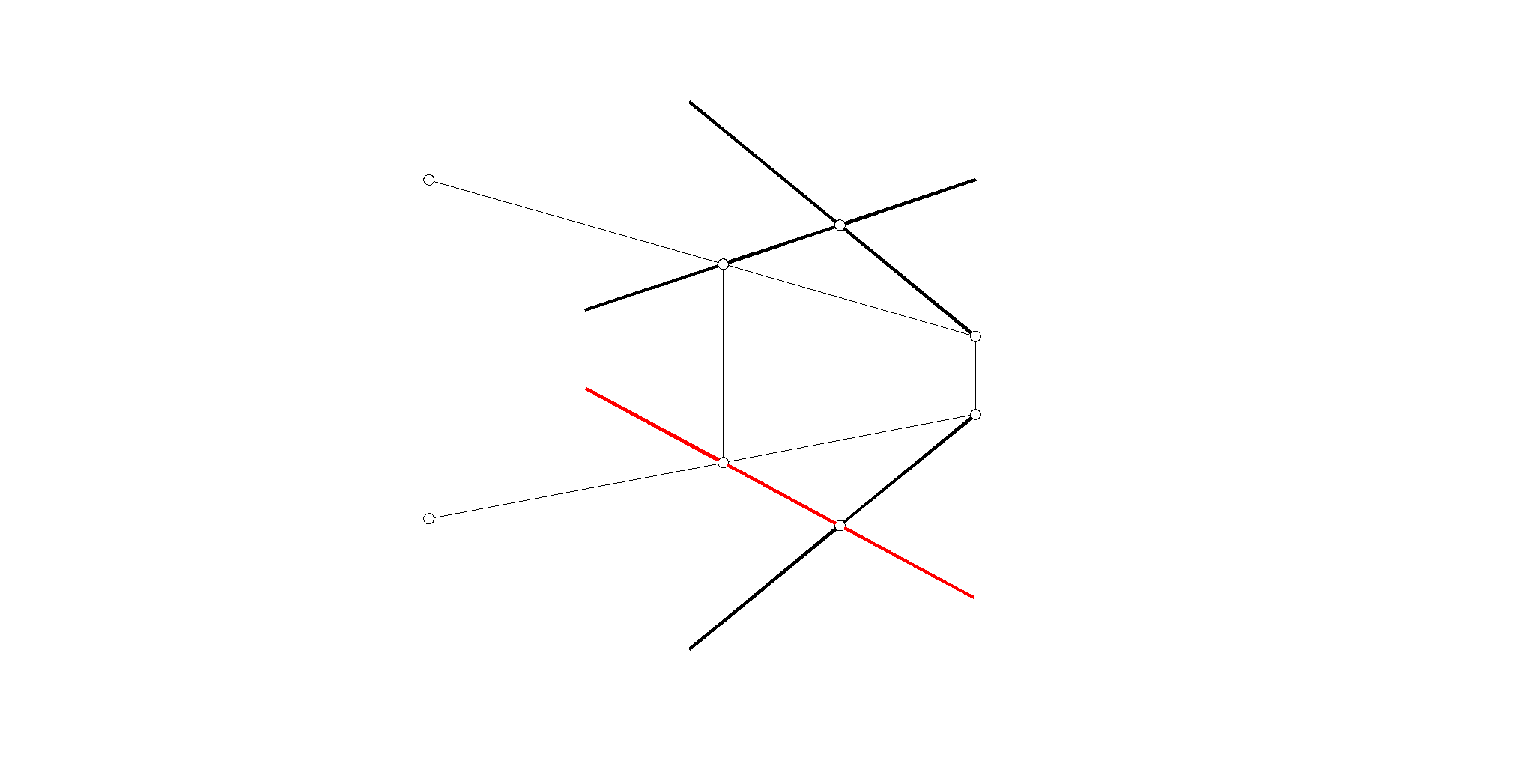
пределить принадлежат ли точки А, В и С плоскости Q (m n).
А 2
В2
В1
m2
С2
С1
A Q B Q С Q
2
m2
. Построить горизонтальную проекцию l1 прямой l, если она принадлежит плоскости Т ( А, m).
А2
А1
12
21
11
l2
l1
Модуль 2 Задачи метрические 4 ПРЕОБРАЗОВАНИЕ КОМПЛЕКСНОГО ЧЕРТЕЖА
4.1 Задачи к разделу 4
Для чего нужны методы преобразования комплексного чертежа?
В чем заключается сущность метода преобразования комплексного чертежа?
Перечислить 4 основные задачи, решаемые методом замены плоскостей проекций.
В чем заключается сущность метода вращения вокруг проецирующей прямой?
_ _________________________________________________________________ _________________________________________________________________
29. Определить натуральную величину отрезка АВ и углы наклона к плоскостям проекций П1 и П2 (метод прямоугольного Δ-ка).
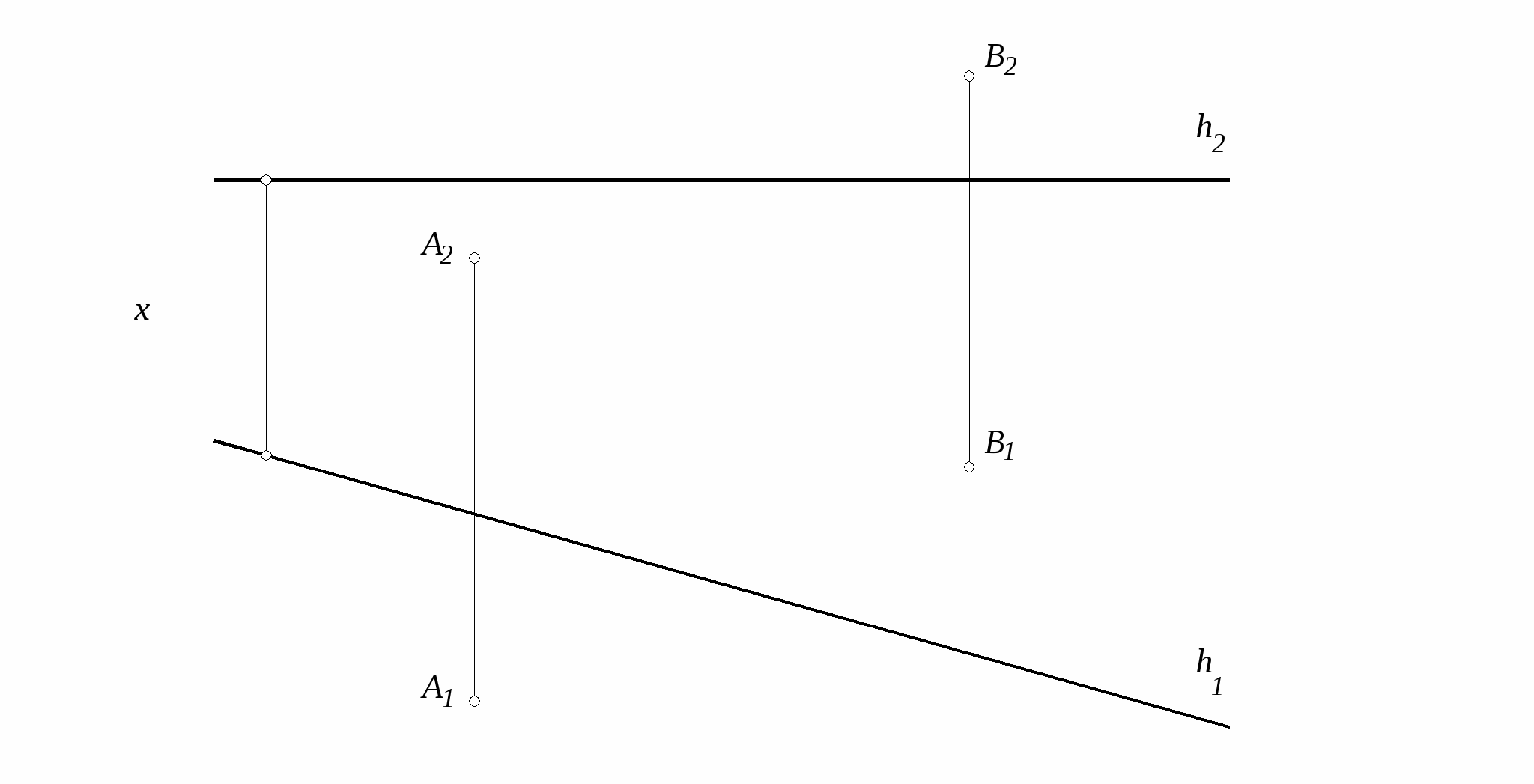
30. Построить проекции точки С, расположенной симметрично точке А. Определить расстояние от точки В до прямой h.
31. Повернуть точки: 32. Построить точку К,
А вокруг i на 180 принадлежащую прямой АВ,
В вокруг i на 90. если АК = 15.
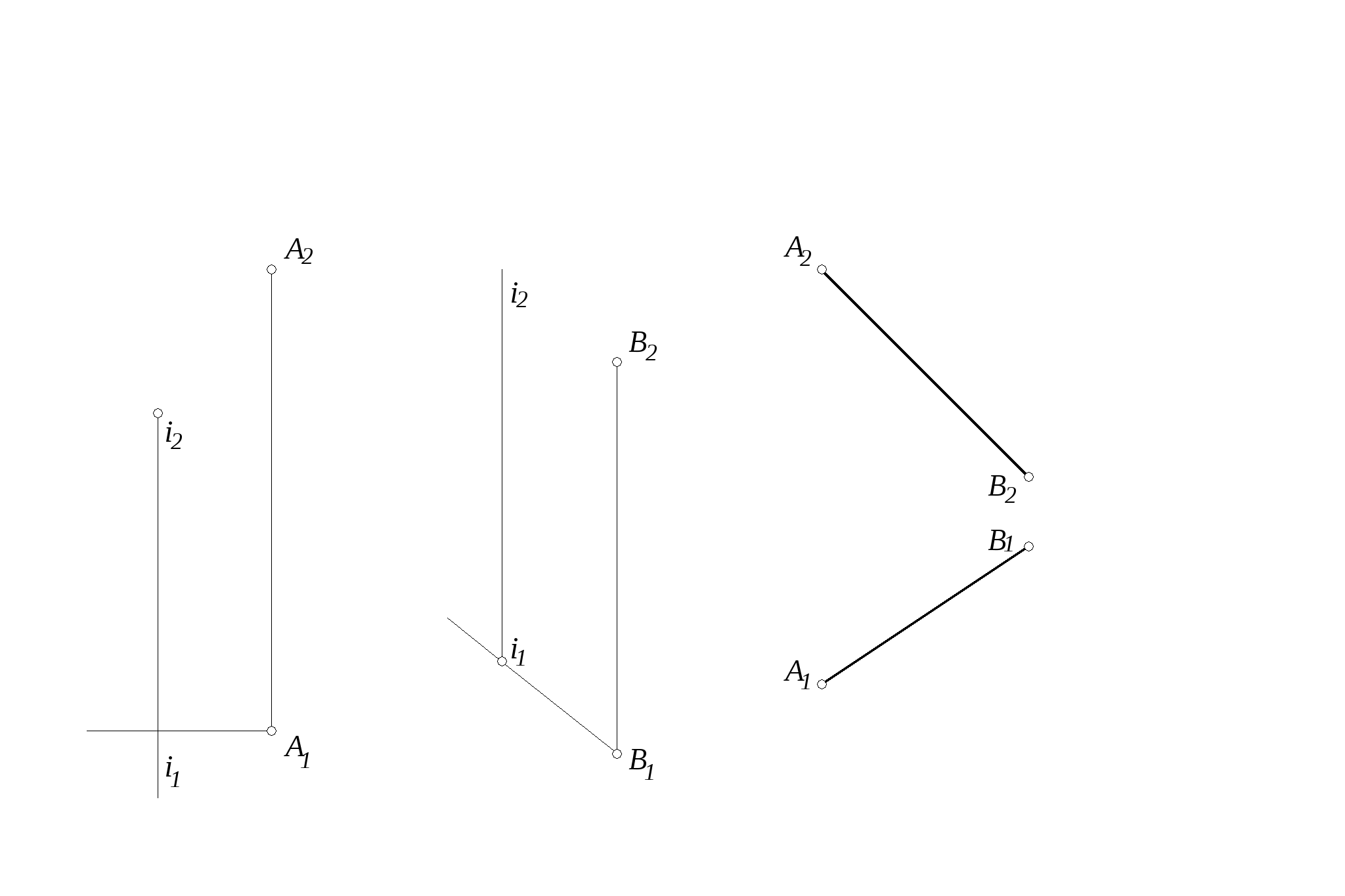
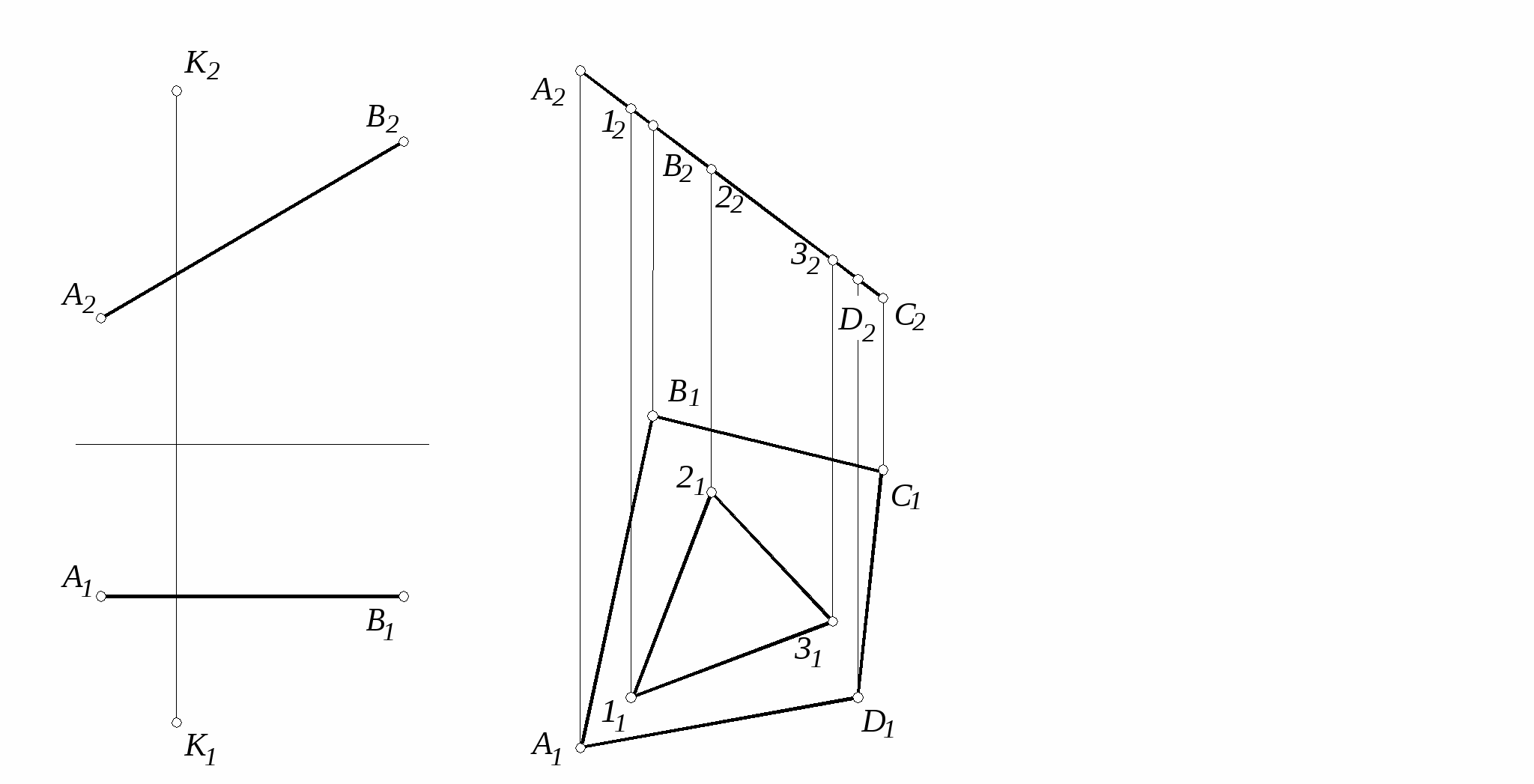
33. Определить расстояние 34. Построить натуральную
от точки К до прямой АВ. величину плоской фигуры.
35. Определить натуральную 36. Определить расстояние от
величину отрезка АВ. точки К до отрезка АВ.

37. Определить натуральную 38. Определить расстояние величину АВС. между прямыми АВ и СD.
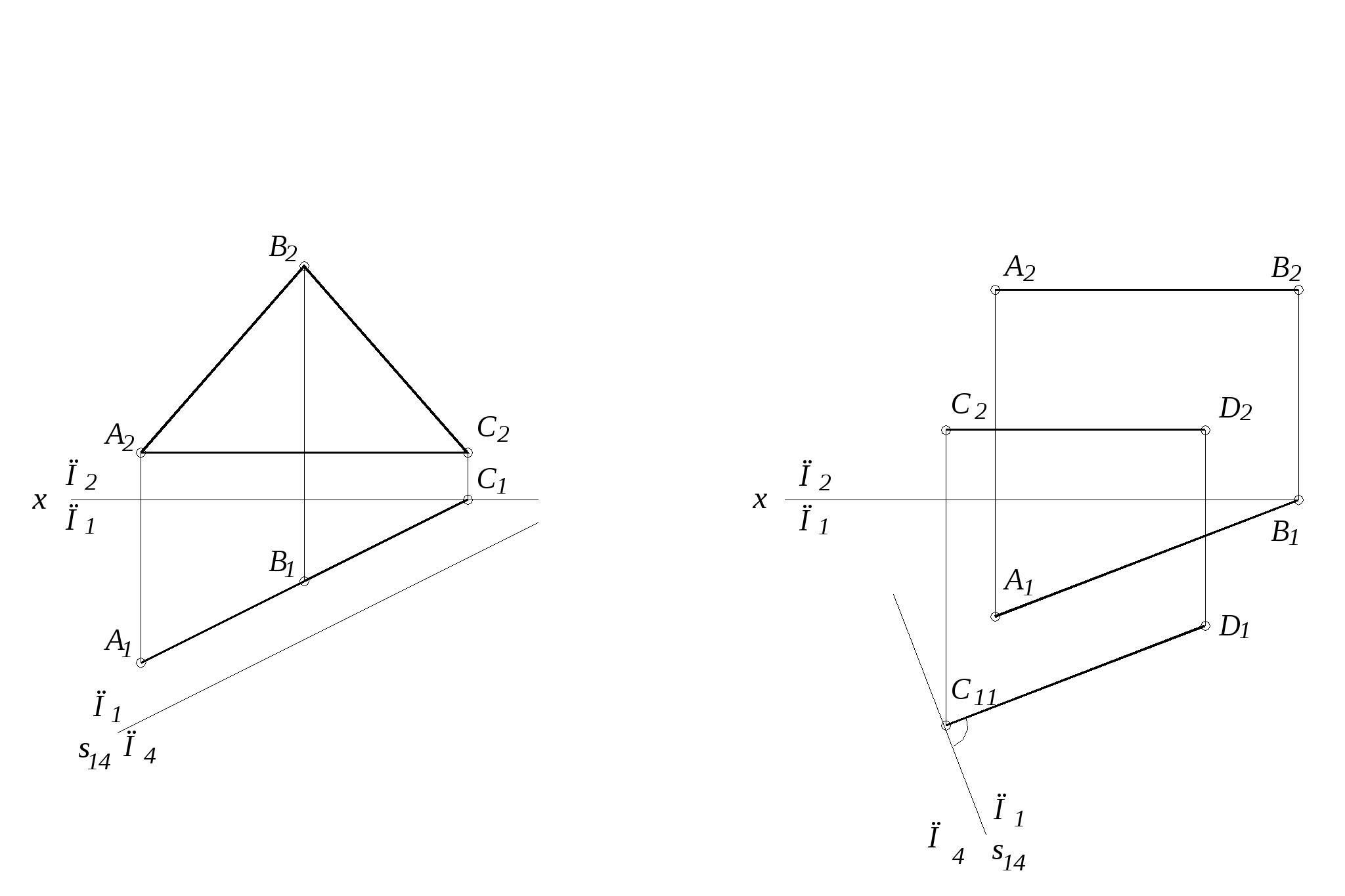
39. Определить кратчайшее расстояние между скрещивающимися
прямыми АВ и CD.
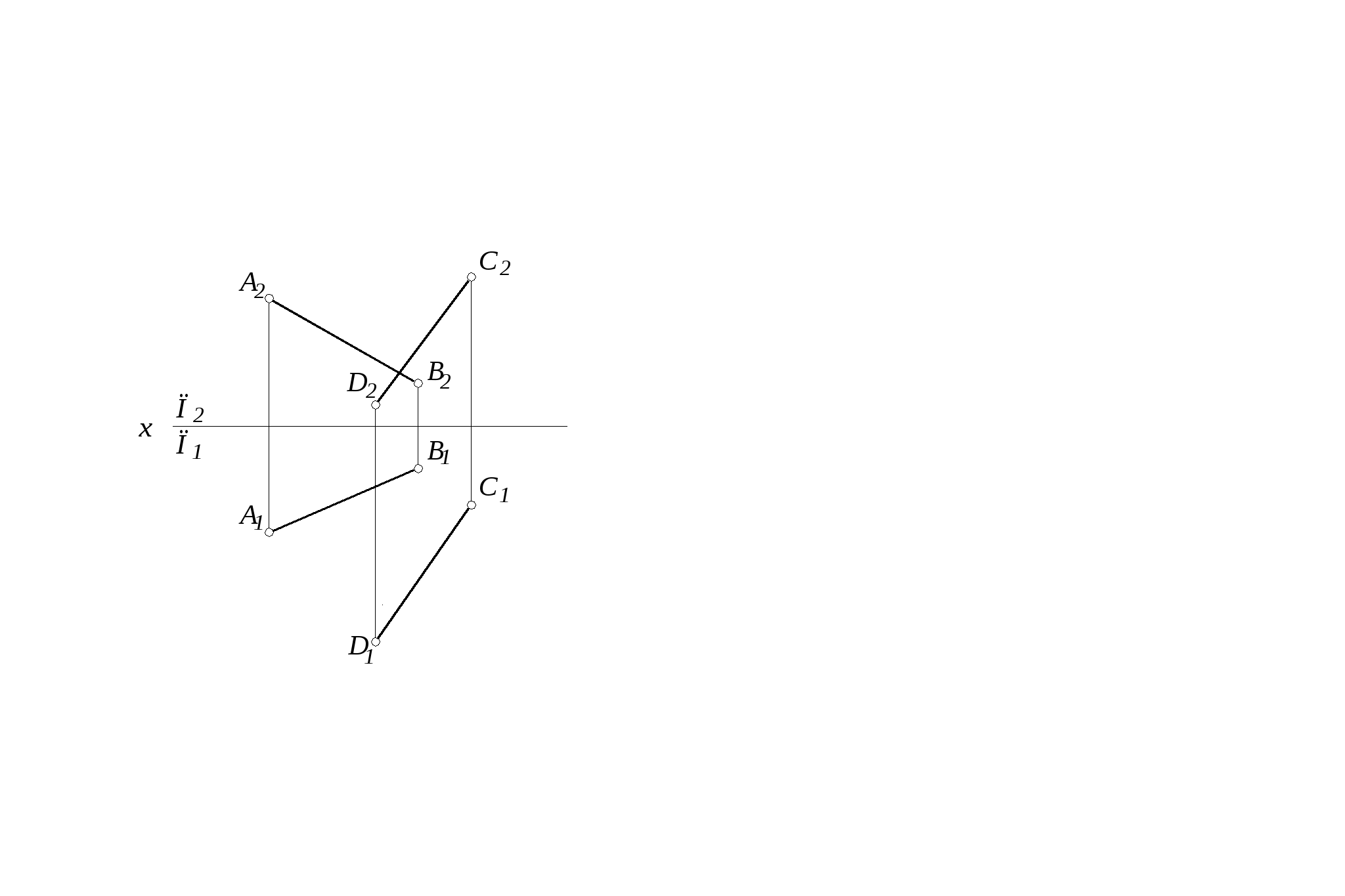
40. Определить расстояние от точки А до плоскости ВСD методом
прямоугольного треугольника.
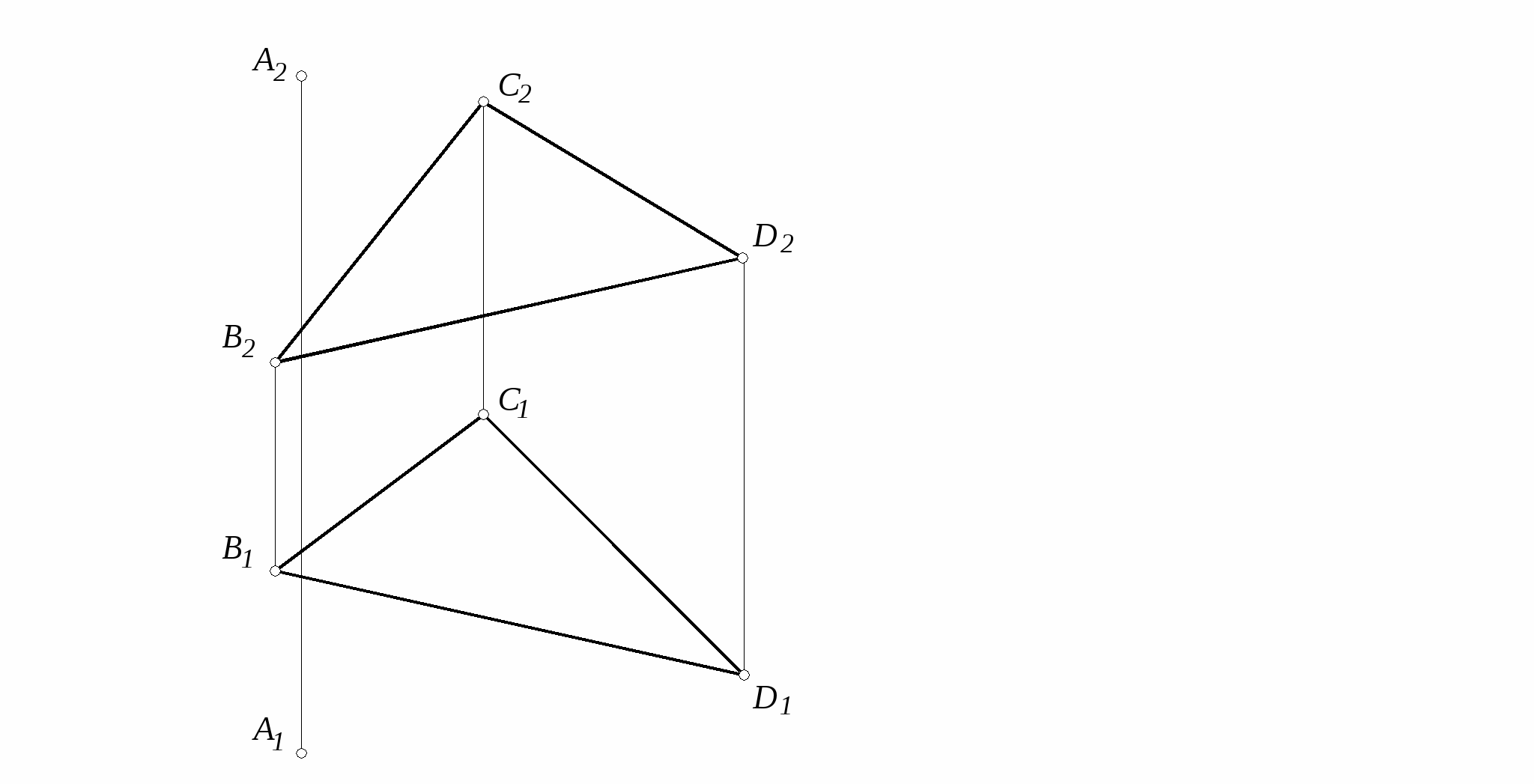
41.Определить величину двугранного угла при ребре АВ
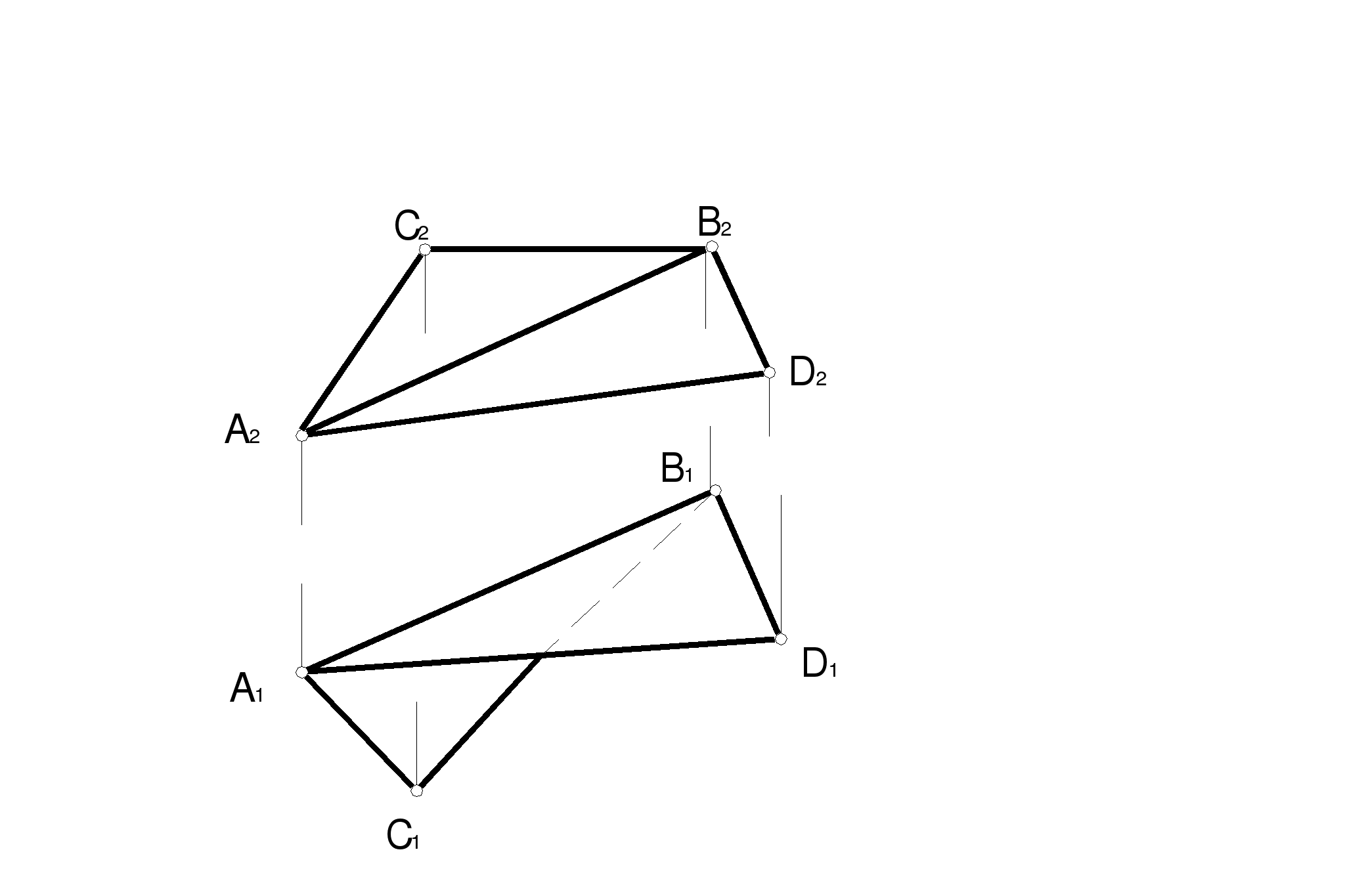 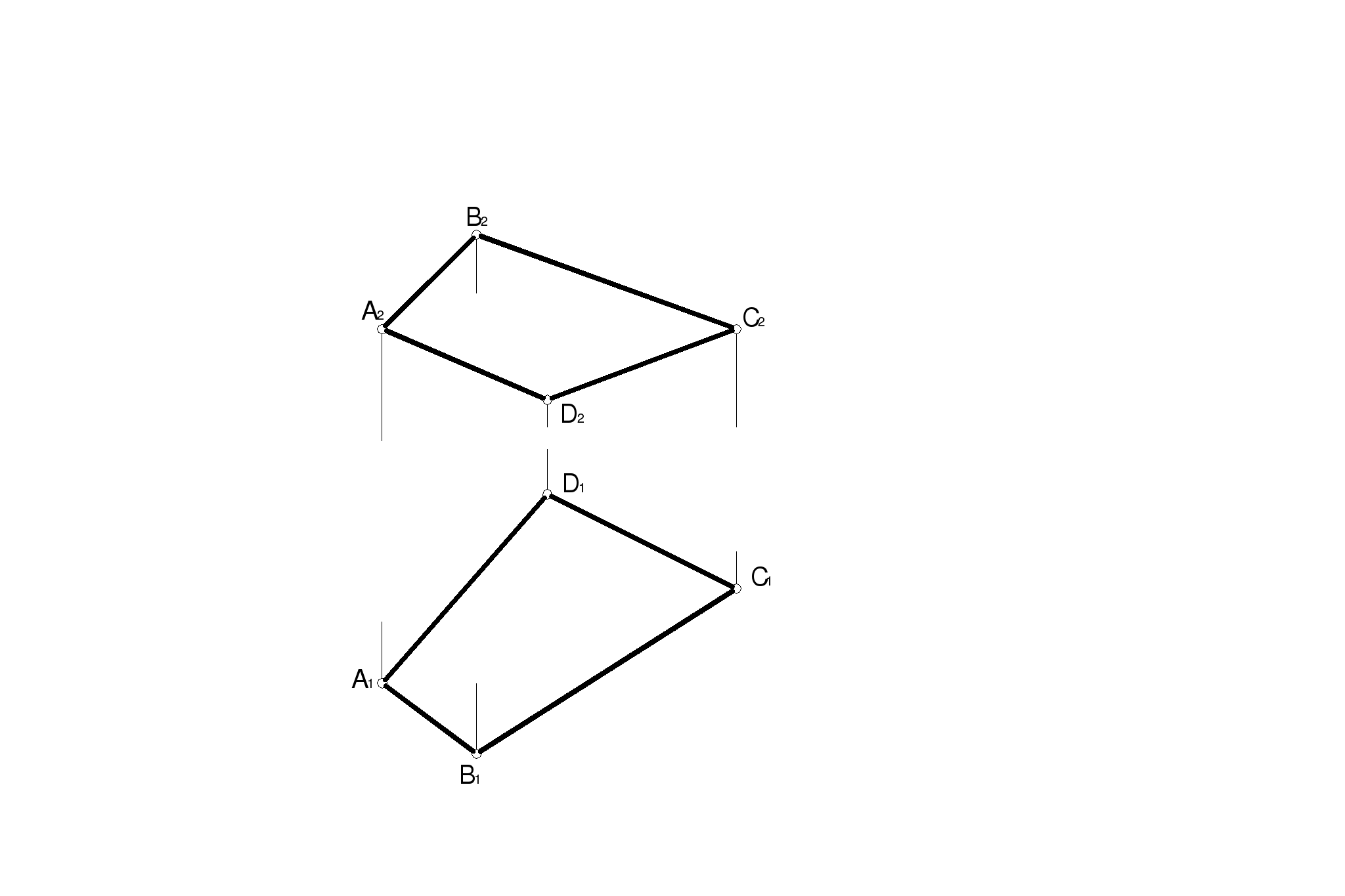
42.Определить натуральную величину четырехугольника АВСD (способом вращения вокруг линии уровня).
4.2 Примеры решения задач раздела 4
1
С2
А1
В4
А4
.Построить равнобедренный треугольник АВС с основанием АВ
и вершиной С, принадлежащей прямой t.
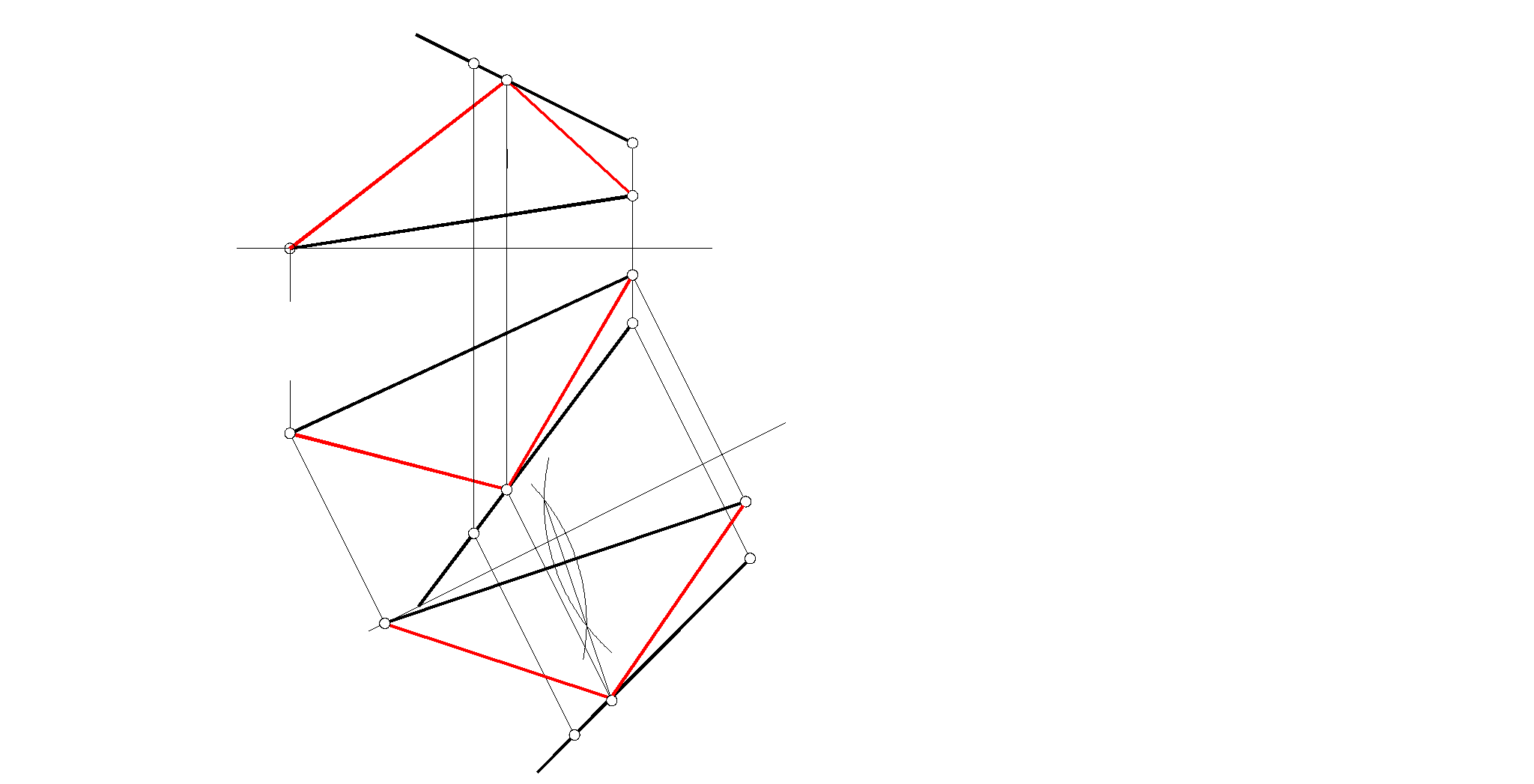
С1
С4
А2
В2
В1
12
11
14
t2
t1
t4
x
П2
П1
s14
П1
П4
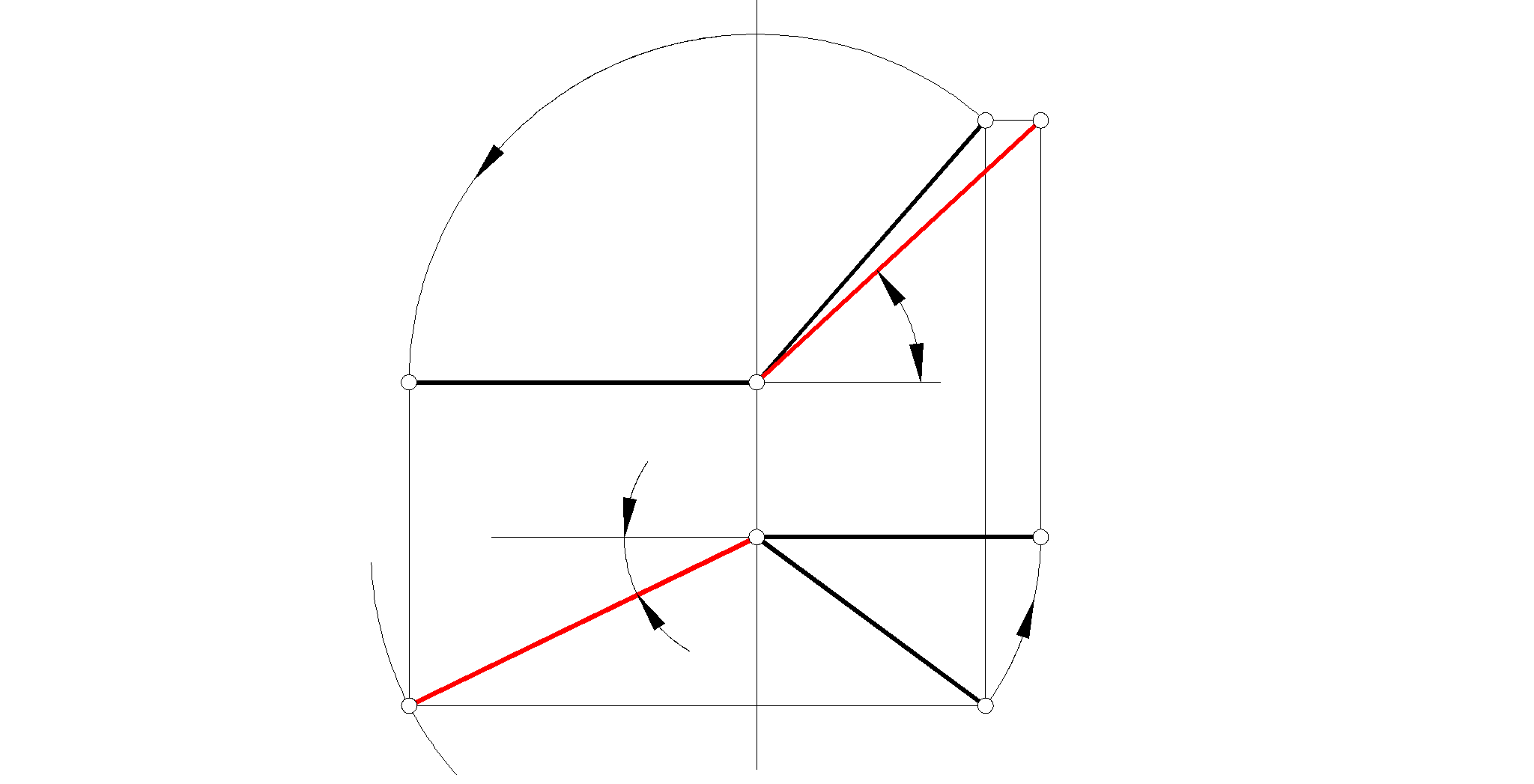
2.Построить горизонтальную проекцию А1В1 отрезка АВ. Длина АВ=45мм. Определить углы наклона и (метод вращения).
i2A2
B2
h2
B1
i1
i1A1
B1
i2
B1
B2
B2
h1
f1
f2
Модуль 3 Поверхности и геометрические тела 5 МНОГОГРАННИКИ 5.1 Задачи к разделу 5
Что называется многогранником?
Что является сечением многогранника плоскостью?
Какие способы построения сечения многогранника плоскостью существуют? В чем заключаются эти способы?
Как формируется алгоритм построения точек пересечения прямой с поверхностью многогранника?
________________________________________________________________
43. Достроить недостающие 44. Определить точки встречи
проекции поверхности и прямой m с многогранником
точек ей принадлежащих. и видимость участков прямой.
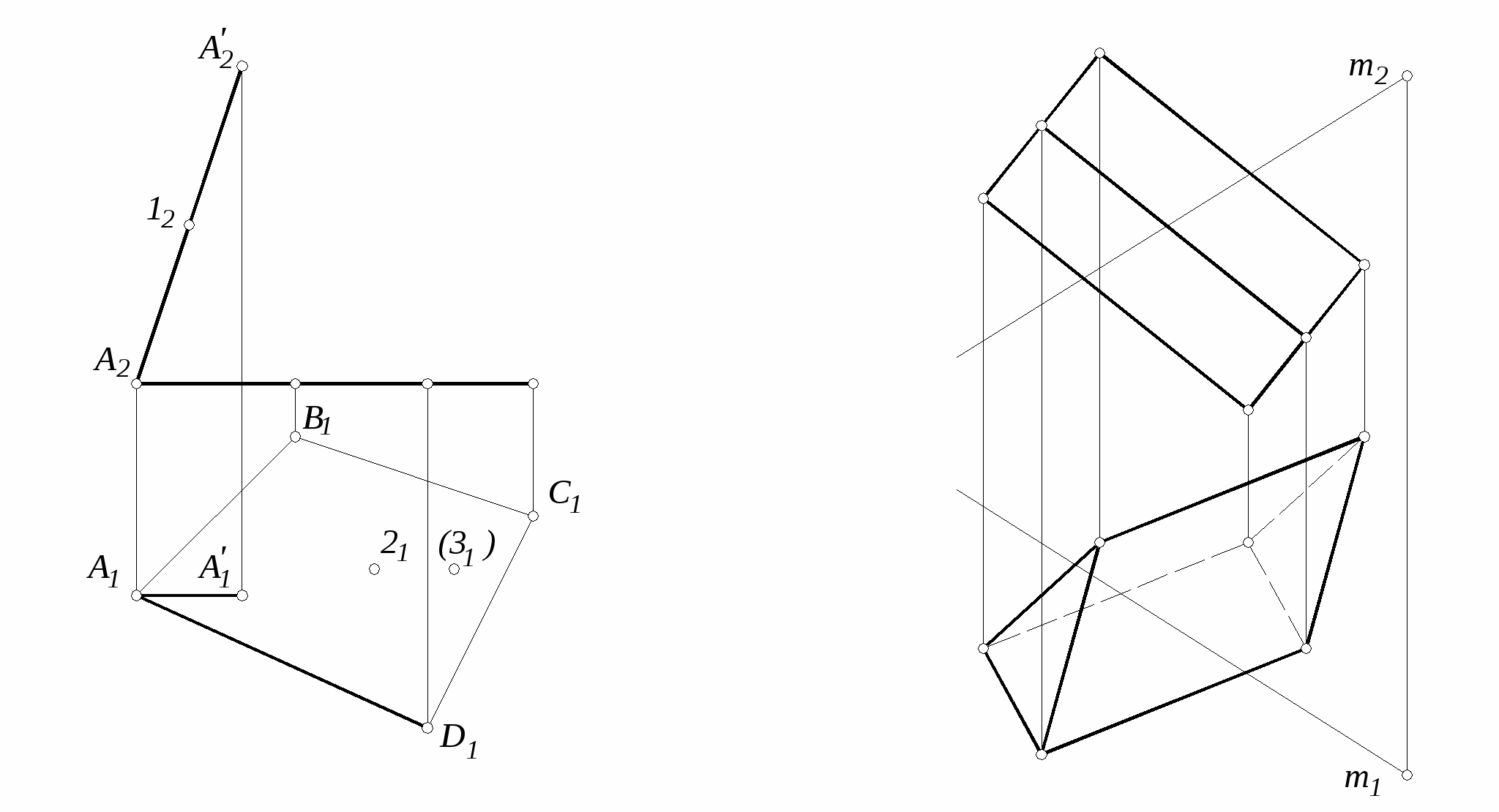 45. Построить профильную проекцию призмы и найти недостающие проекции точек, принадлежащих граням этой призмы. Определить положение ребер и граней призмы относительно плоскостей проекций 45. Построить профильную проекцию призмы и найти недостающие проекции точек, принадлежащих граням этой призмы. Определить положение ребер и граней призмы относительно плоскостей проекций
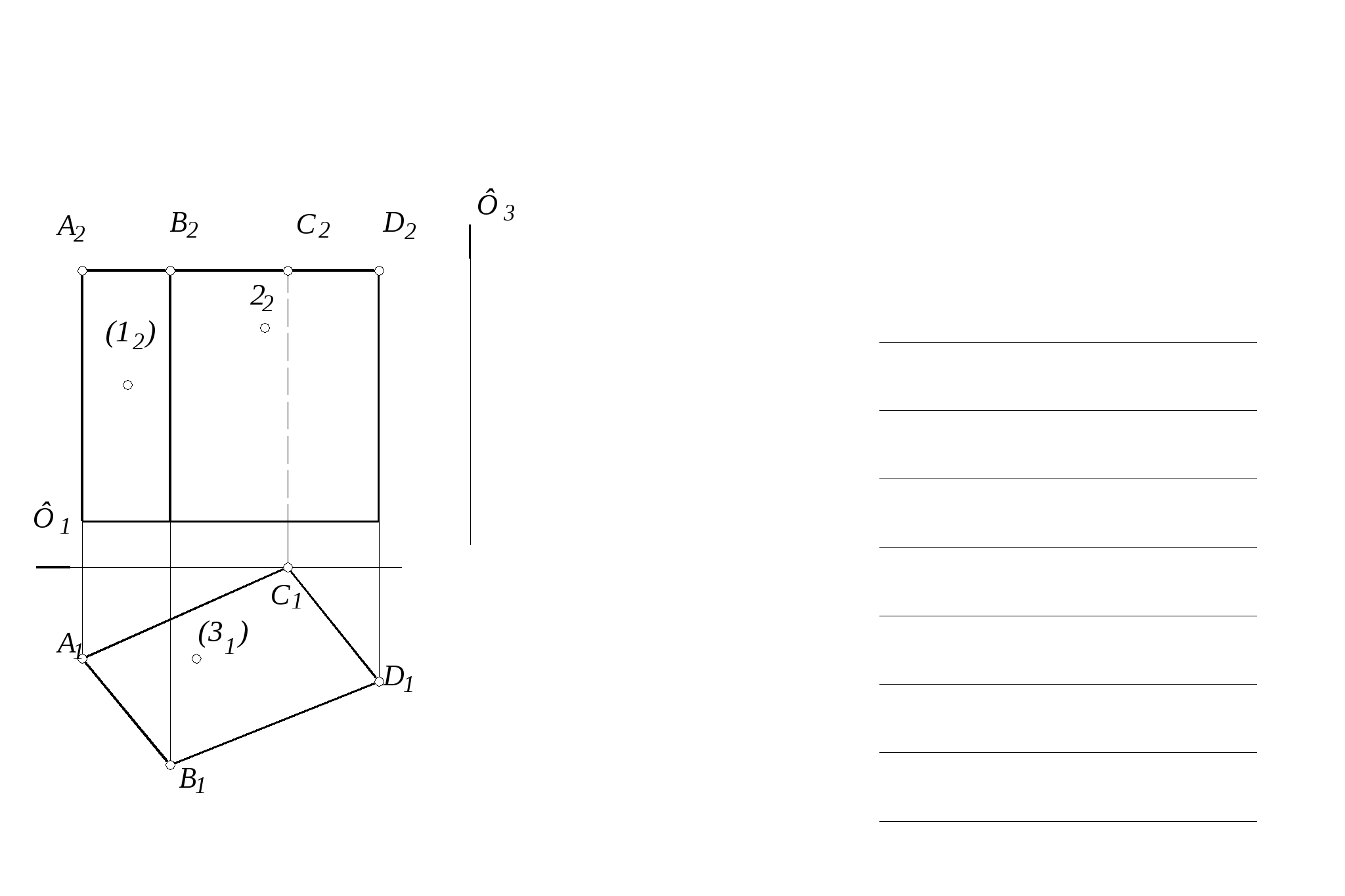
46. Построить три проекции линии пересечения поверхности призмы
с плоскостью . Определить натуральную величину фигуры
сечения. Построить полную развертку усеченной части призмы.
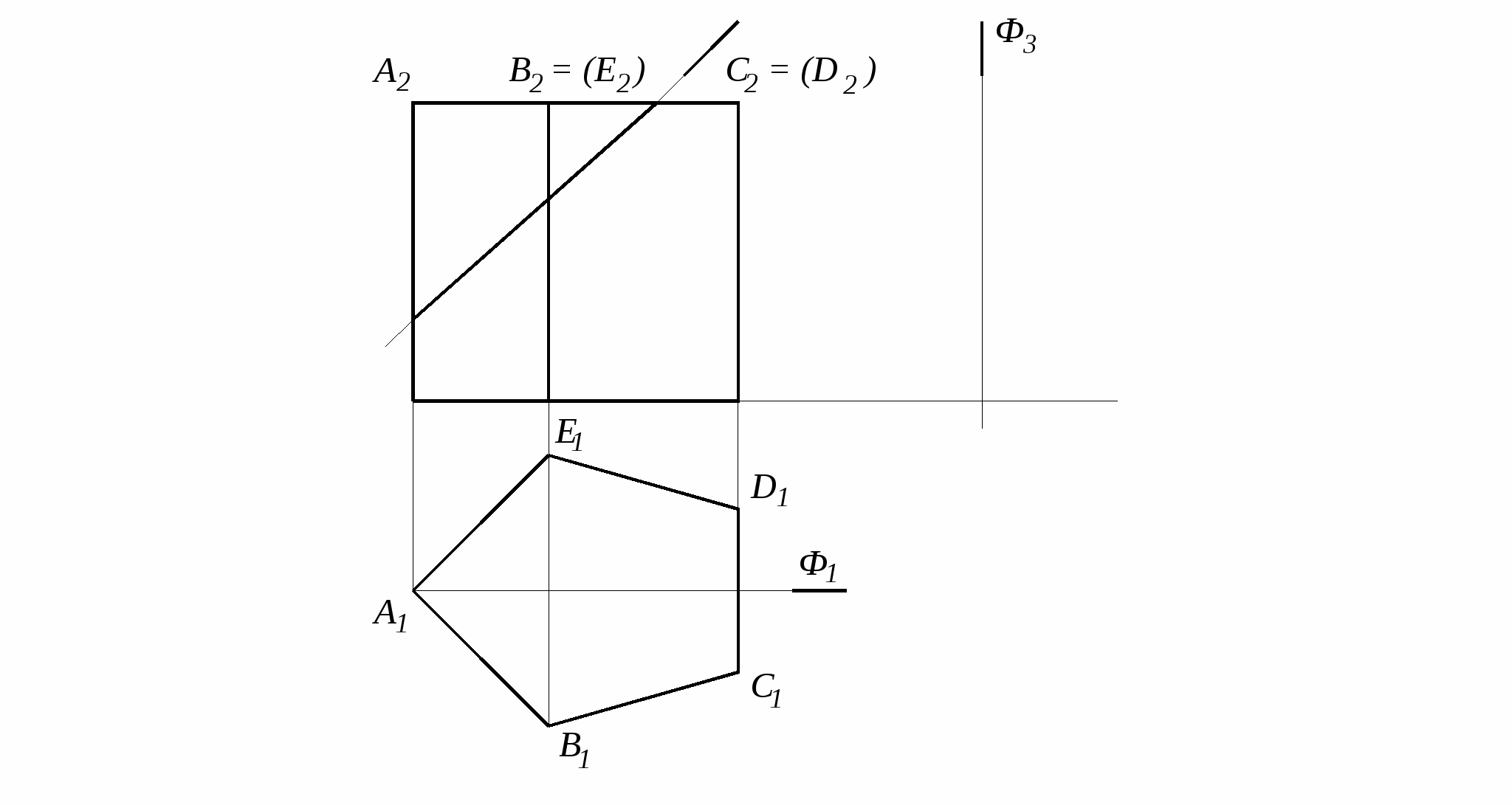

47. Построить три проекции призмы со сквозным отверстием (вырезом).
а)
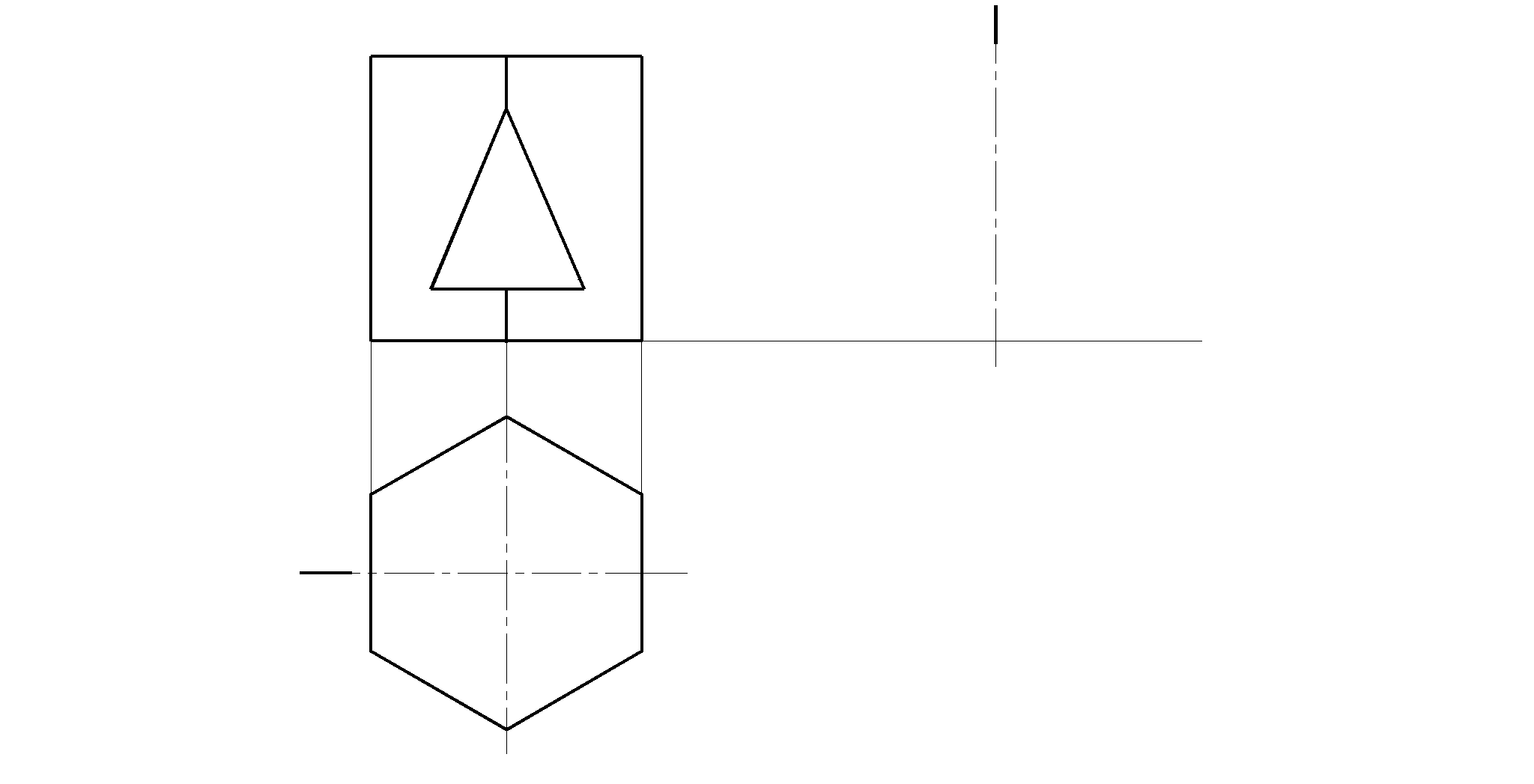
б)
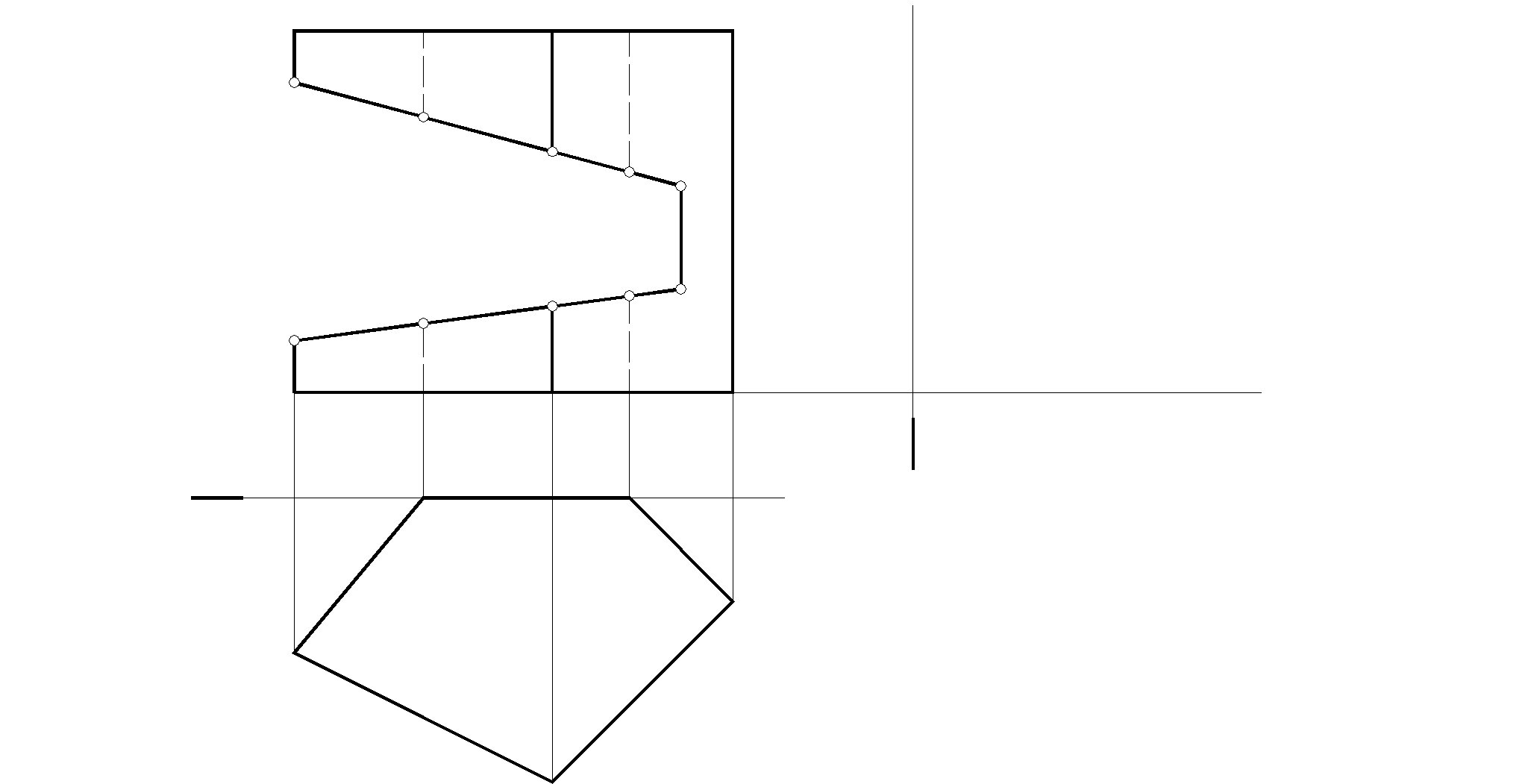
48. Достроить недостающие 49. Определить точки встречи
проекции поверхности и прямой l с многогранником
точек ей принадлежащих. и видимость участков прямой.
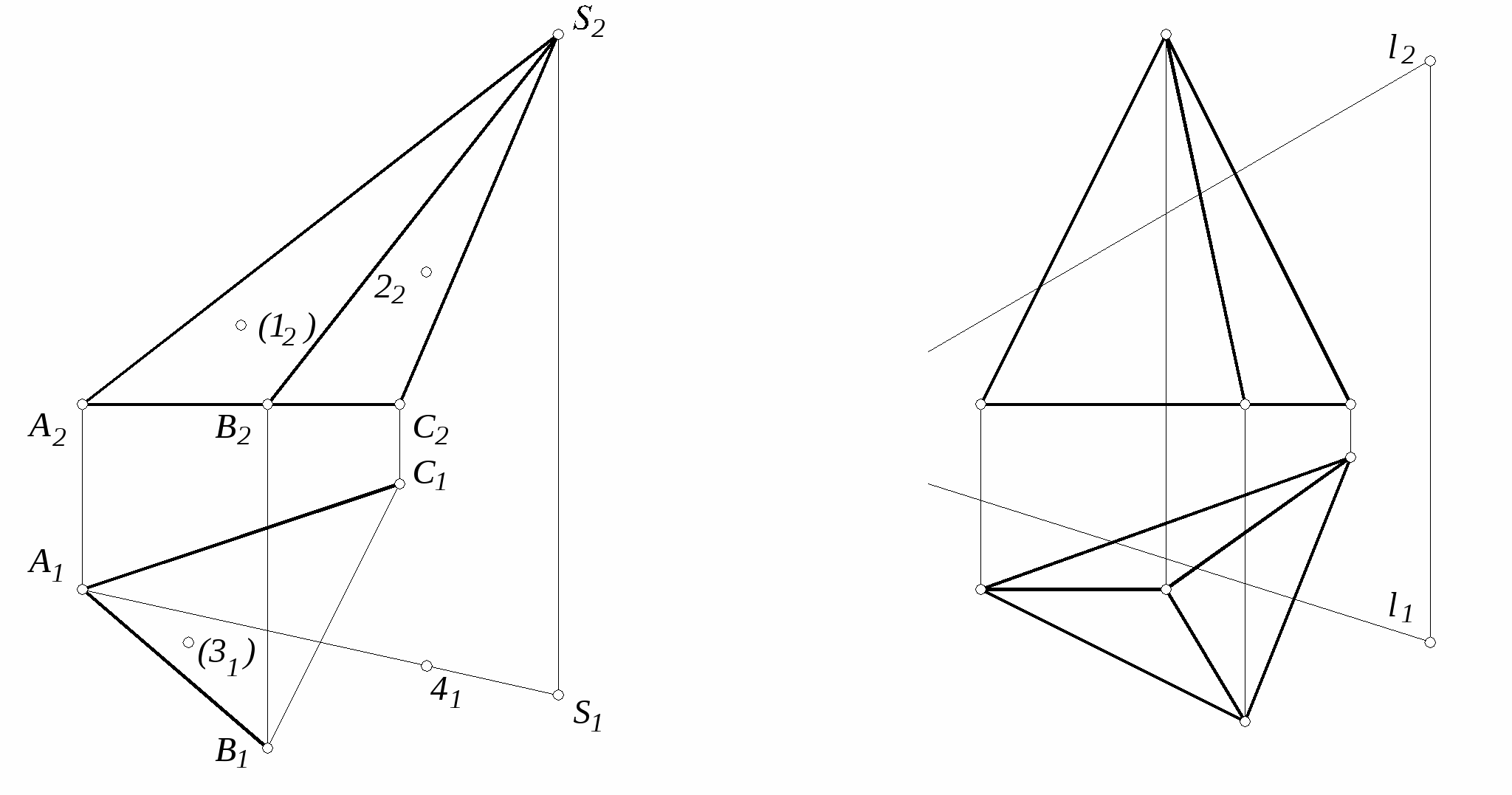
50. Построить профильную проекцию пирамиды и найти недостающие проекции точек, принадлежащих граням этой пирамиды. Определить положение ребер и граней пирамиды относительно плоскостей проекций
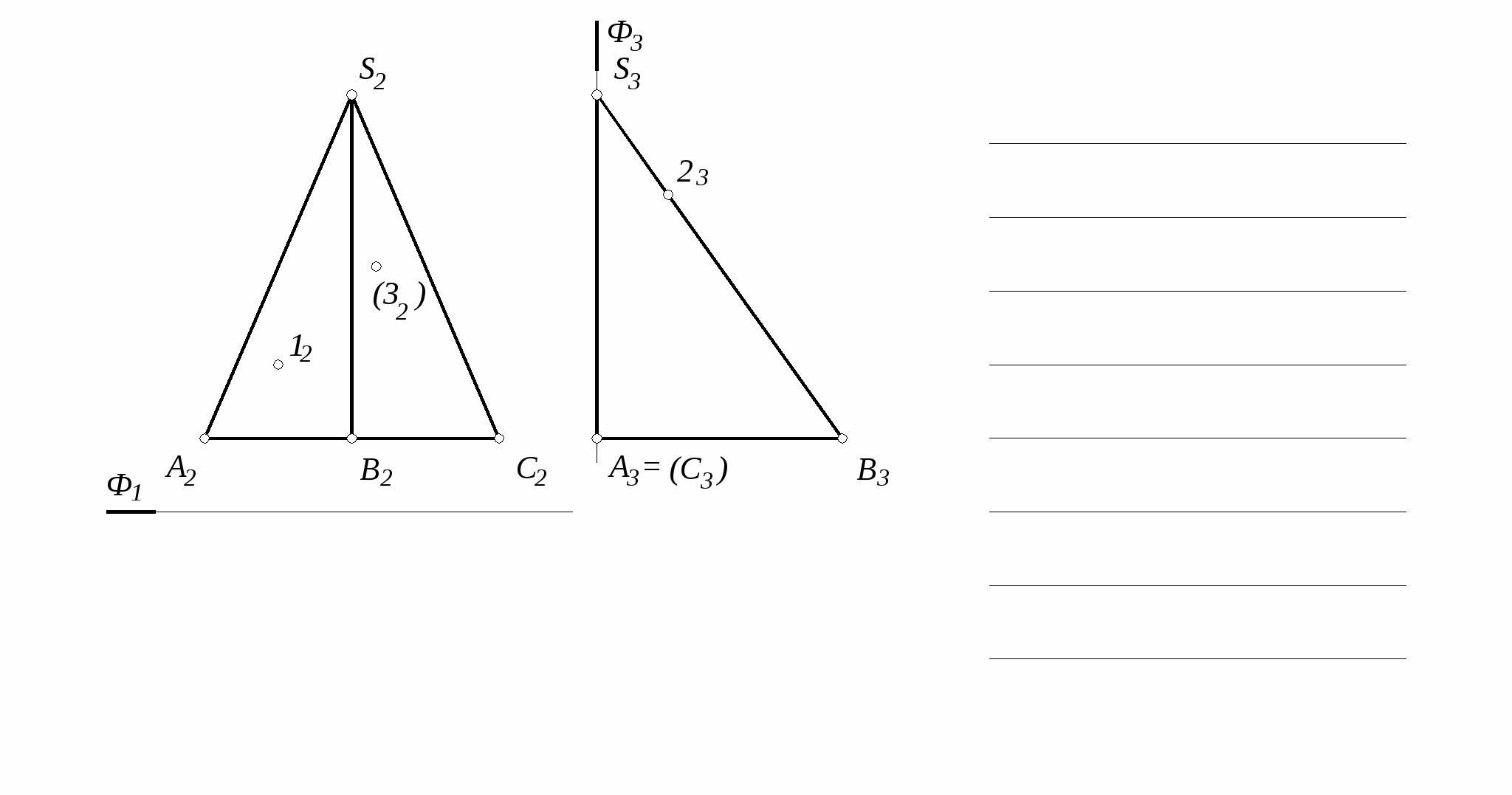
51. Построить три проекции линии пересечения поверхности пирамиды с плоскостью . Определить натуральную величину фигуры сечения. Построить полную развертку усеченной части пирамиды.
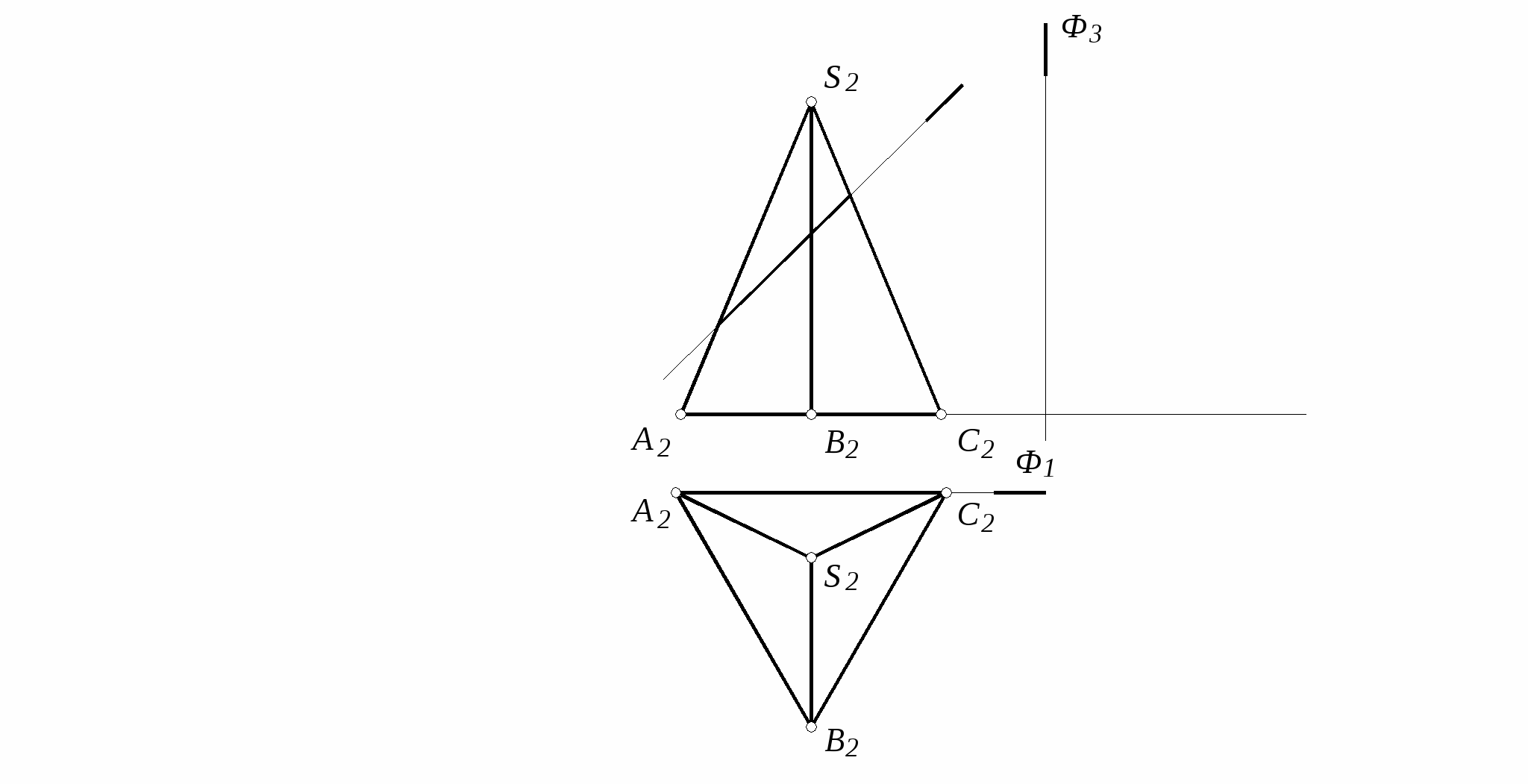
52. Построить три проекции пирамиды с вырезом (сквозным отверстием)
а)
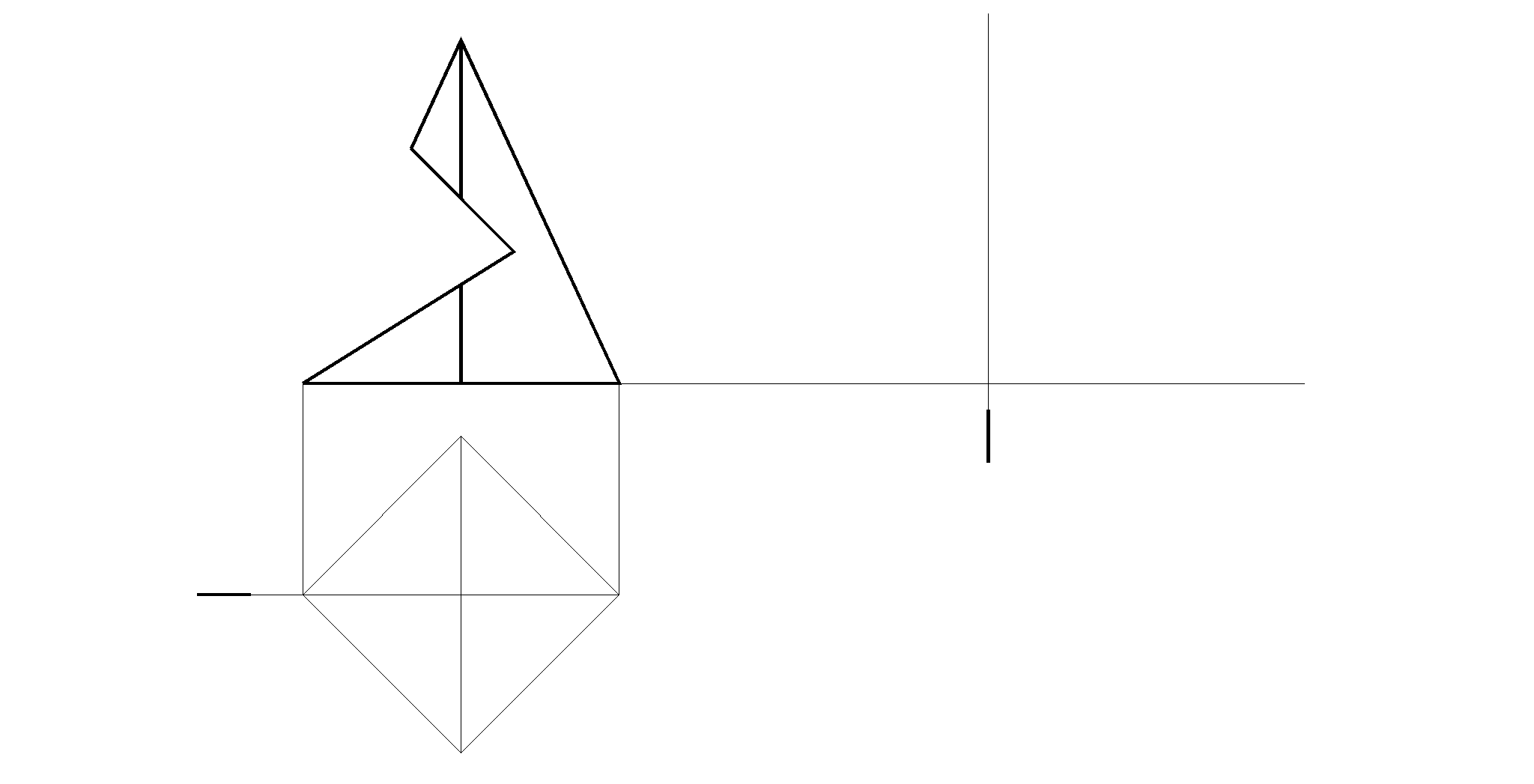
б)
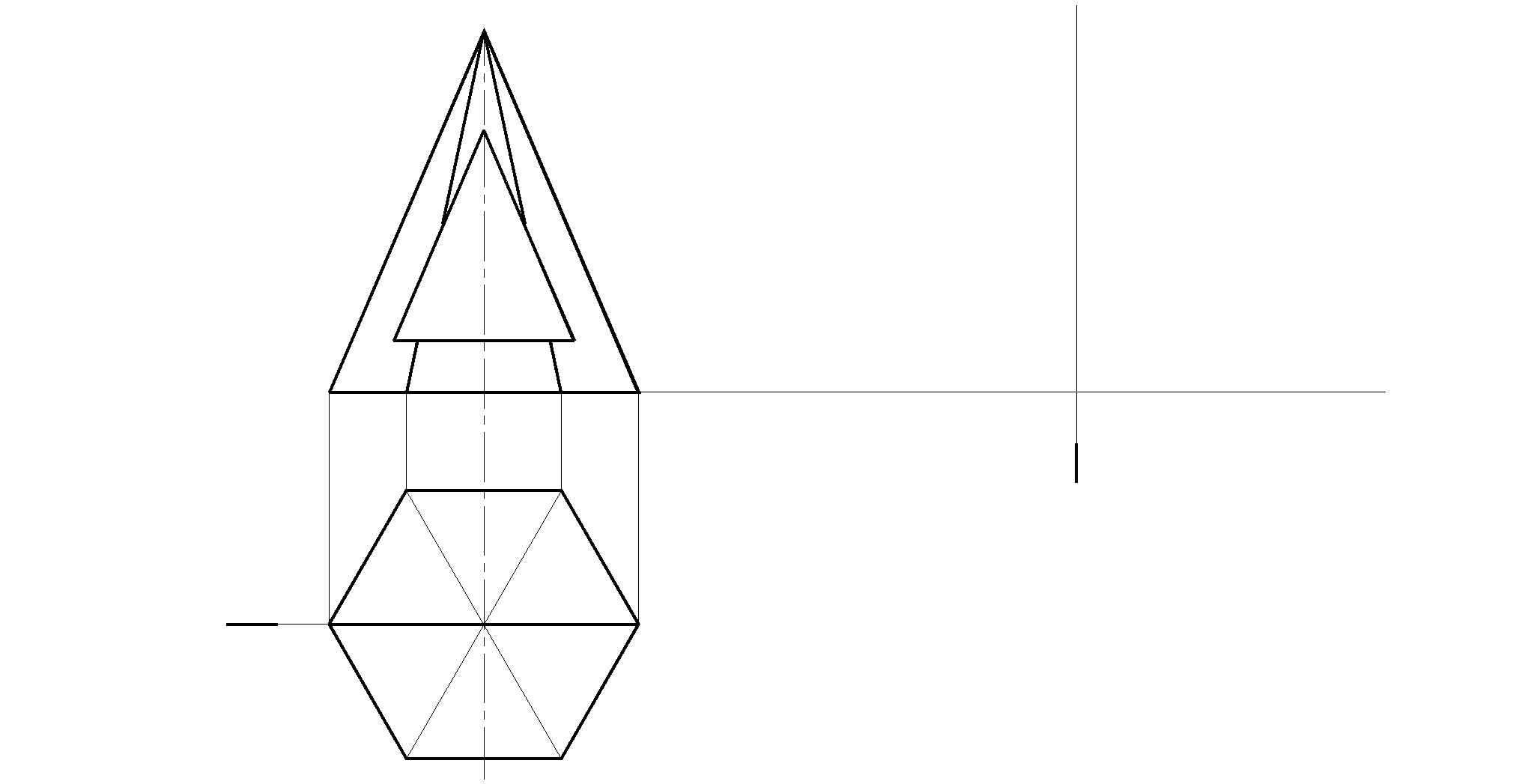
5.2 Примеры решения задач раздела 5
1
12(22)
(В3)
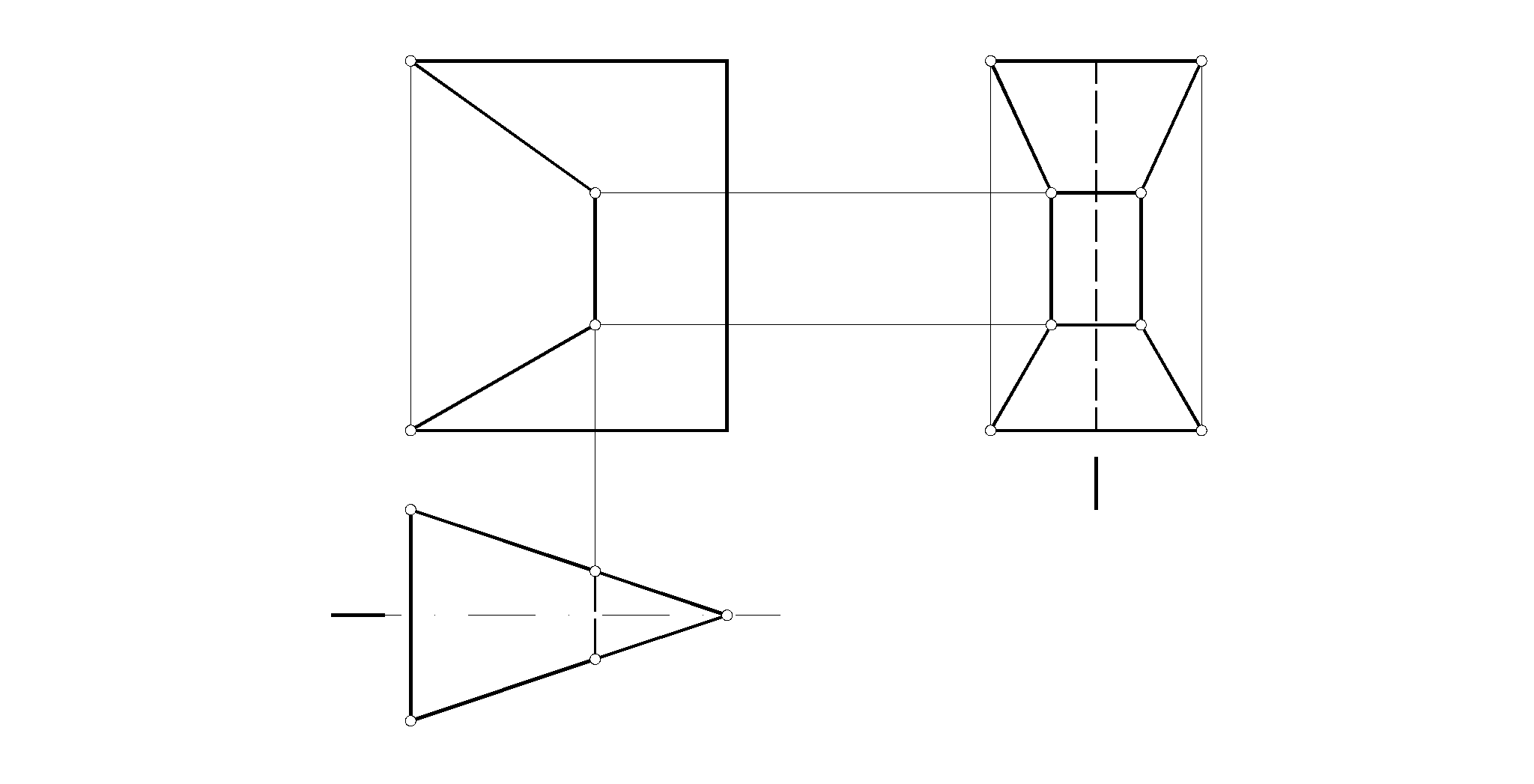
. Построить три проекции призмы с вырезом
23
13
В2
32(42)
52(62)
72(82)
Ф1
Ф3
А121(81)
С111(71)
(41)(61)
(31)(51)
В1
43
33
63
53
83
73
А2(С2)
А3
С3
2
S2
S3
. Построить три проекции пирамиды с вырезом

12(22)
32(42)
52(62)
72(82)
11
21
71
81
51
61
31
41
23
13
33
41
83(63)
73(53)
А1
D3
A2(D2)
S1
B1
C1
B2(C2)
D3(C3)
A3(B3)
Г2
Ф1
Ф3
6 ПОВЕРХНОСТИ ВРАЩЕНИЯ
6.1 Задачи к разделу 6
Что называется поверхностью вращения?
Укажите основные свойства поверхностей вращения.
Какие линии на поверхности вращения называются: параллелью, экватором, меридианом?
Какие фигуры могут быть получены при рассечении плоскостью кругового цилиндра, конуса, сферы?
Назовите методы нахождения точек на поверхностях вращения.
Как найти точки, принадлежащие сечению геометрического тела плоскостью?
Какие точки сечения называются опорными, случайными?
Сформулируйте алгоритм нахождения точек пересечения прямой с поверхностью вращения.
________________________________________________________________
Д
m2
12
32
i2
m1
i1
21
11
22
A2
B2
C2
i1
B1≡C1
остроить недостающие проекции поверхностей и точек, принадлежащих данным поверхностям.
53. 54.
A1
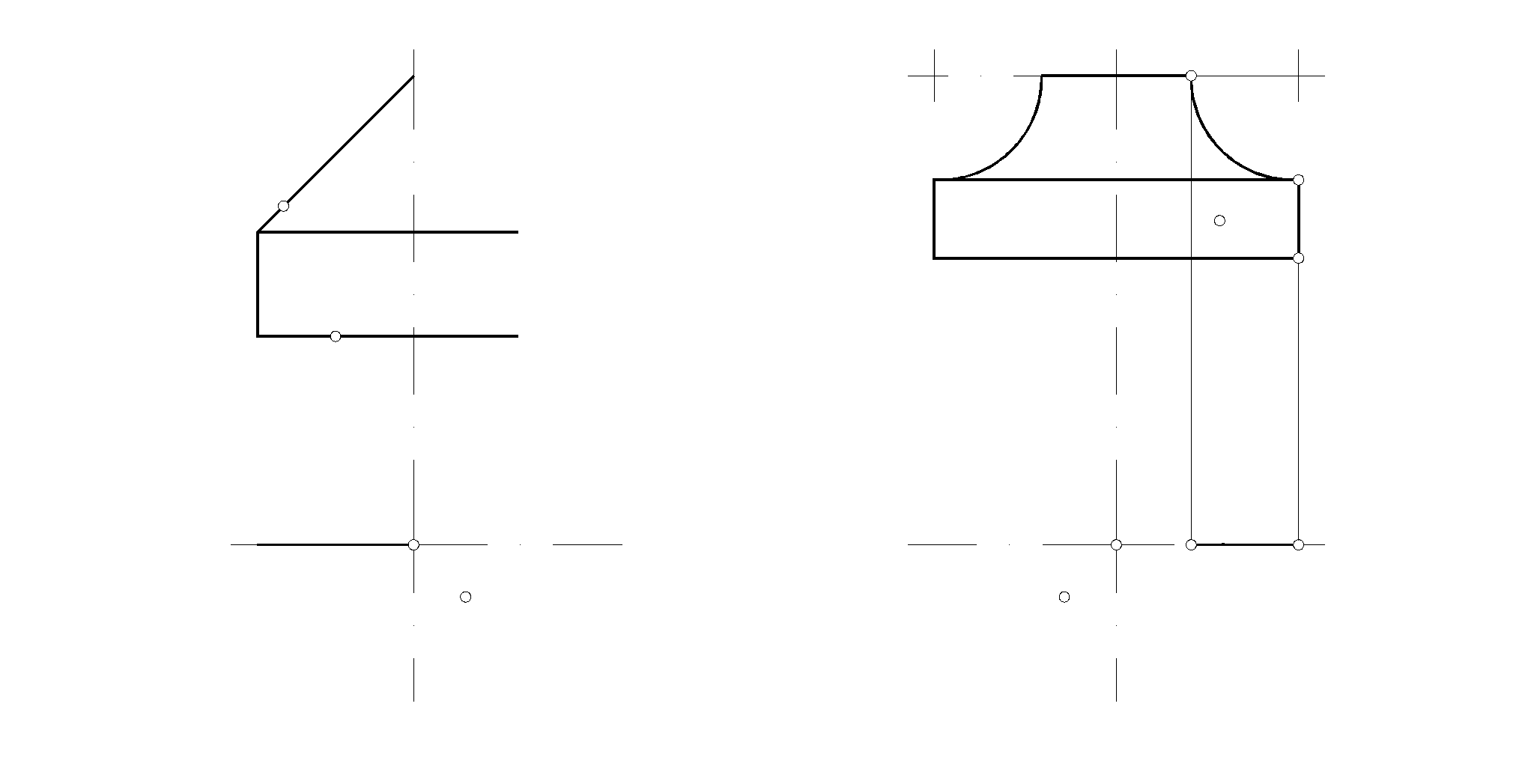
55. Построить три проекции линии пересечения поверхности цилиндра с плоскостью . Определить натуральную величину фигуры, полученной в пересечении. Построить полную развертку усеченной части цилиндра.
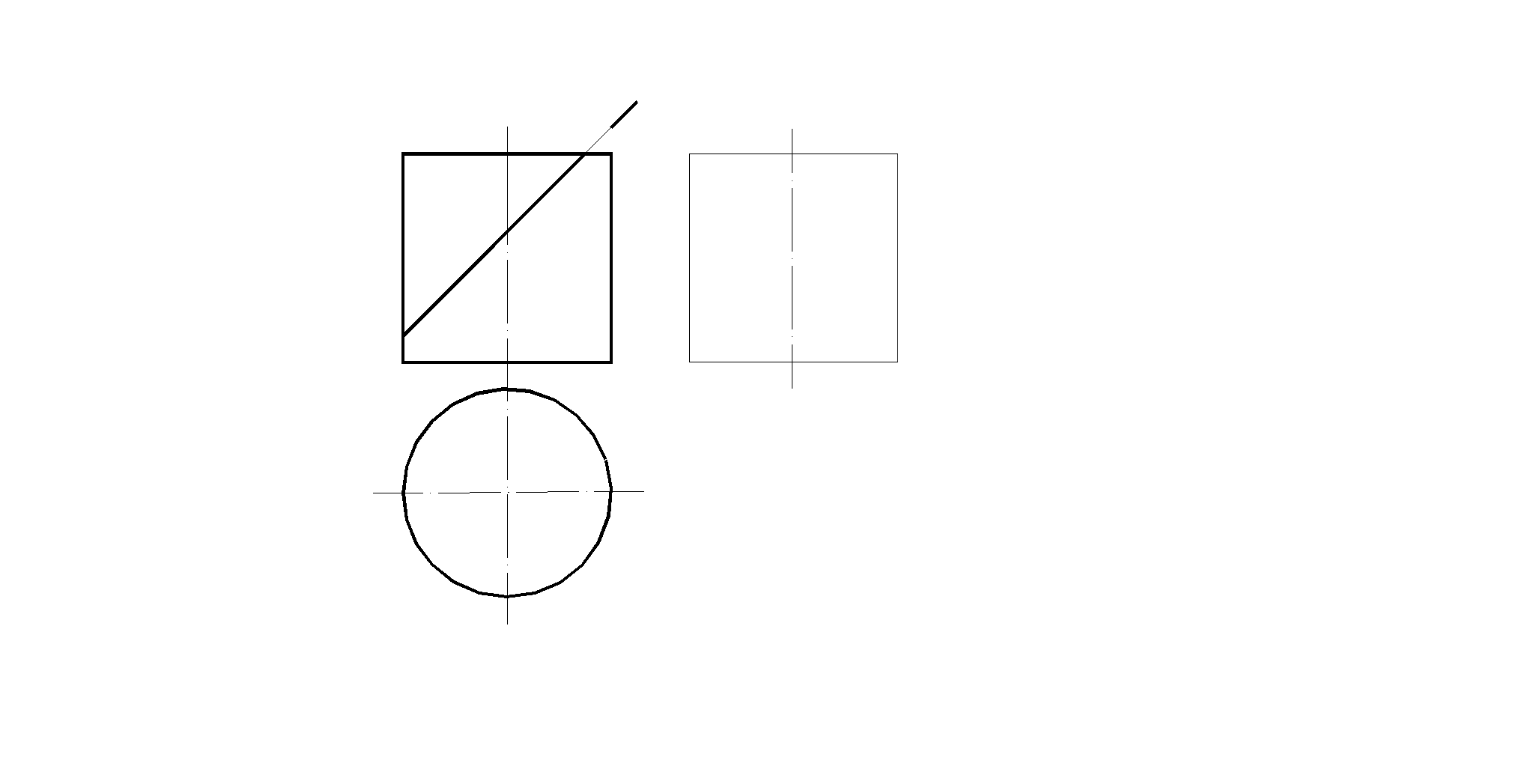
2
56. Построить проекции цилиндра с вырезом.

Ф1
Ф3
    
57. Построить проекции точек пересечения прямых l и m с поверхностью цилиндра. Определить участки видимости прямых.
а) б)
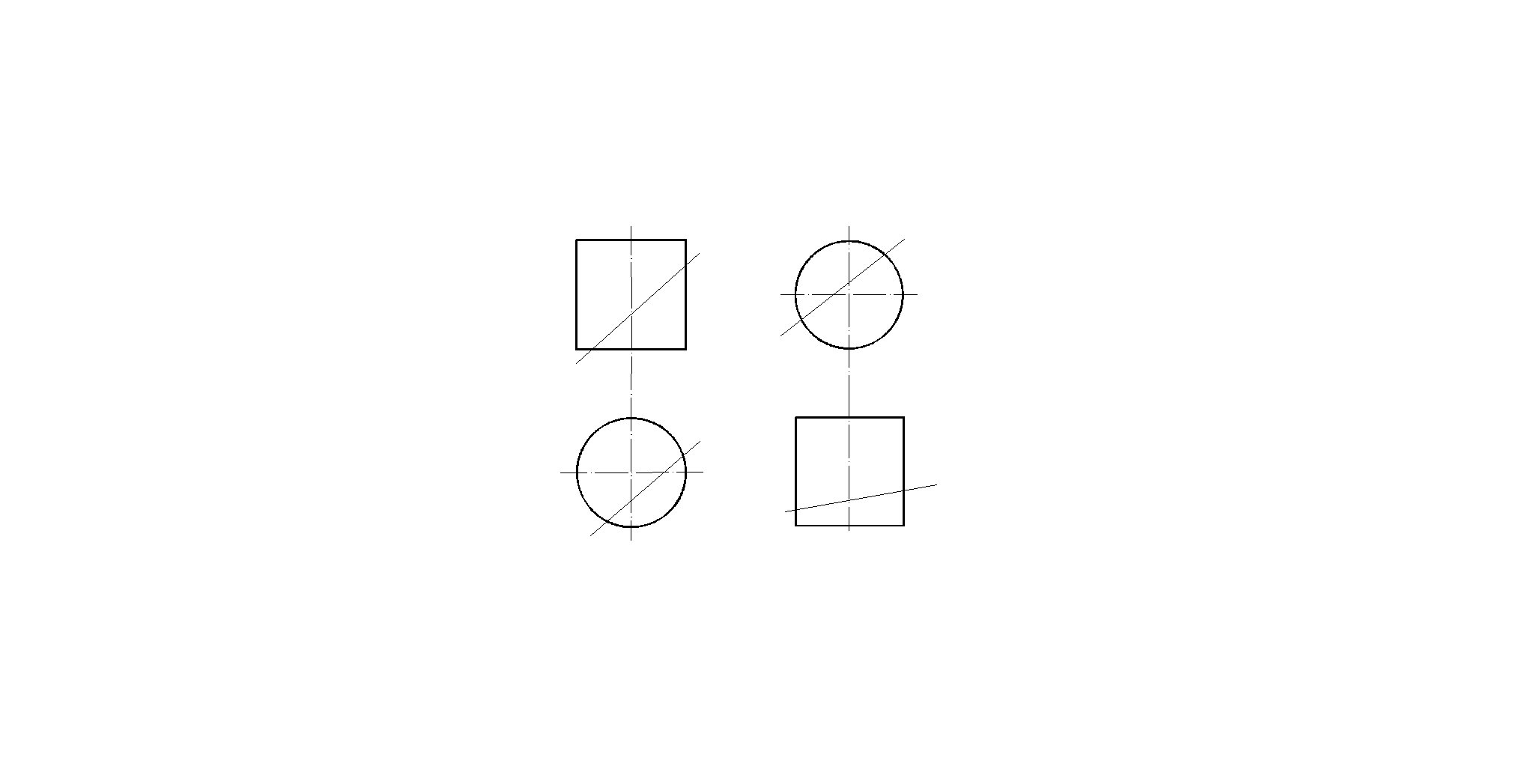
l2
l1
m2
m1
58. Построить три проекции линии пересечения поверхности конуса плоскостью . Определить натуральную величину фигуры сечения. Построить полную развертку усеченной части конуса.
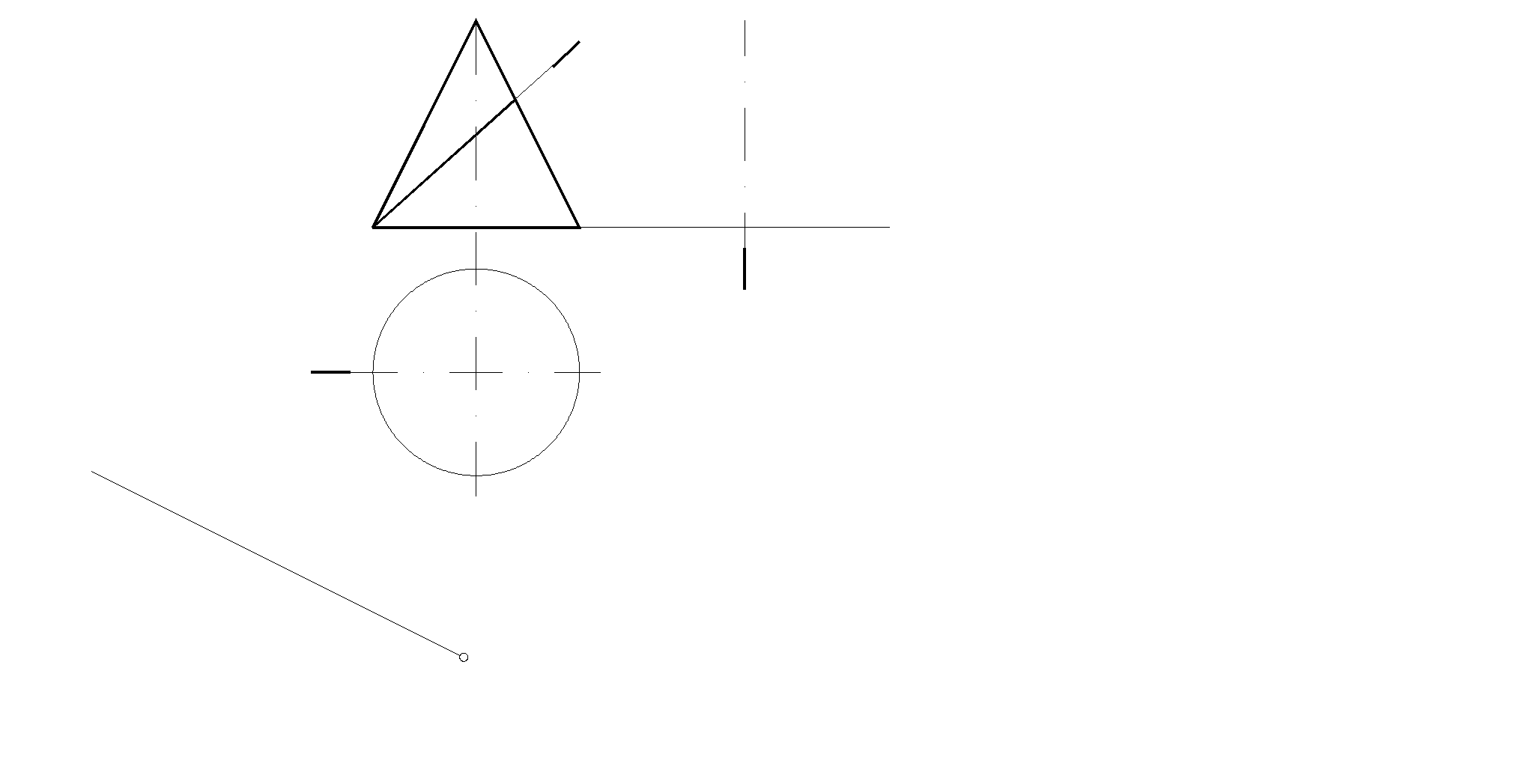
59. Построить три проекции конуса с вырезом
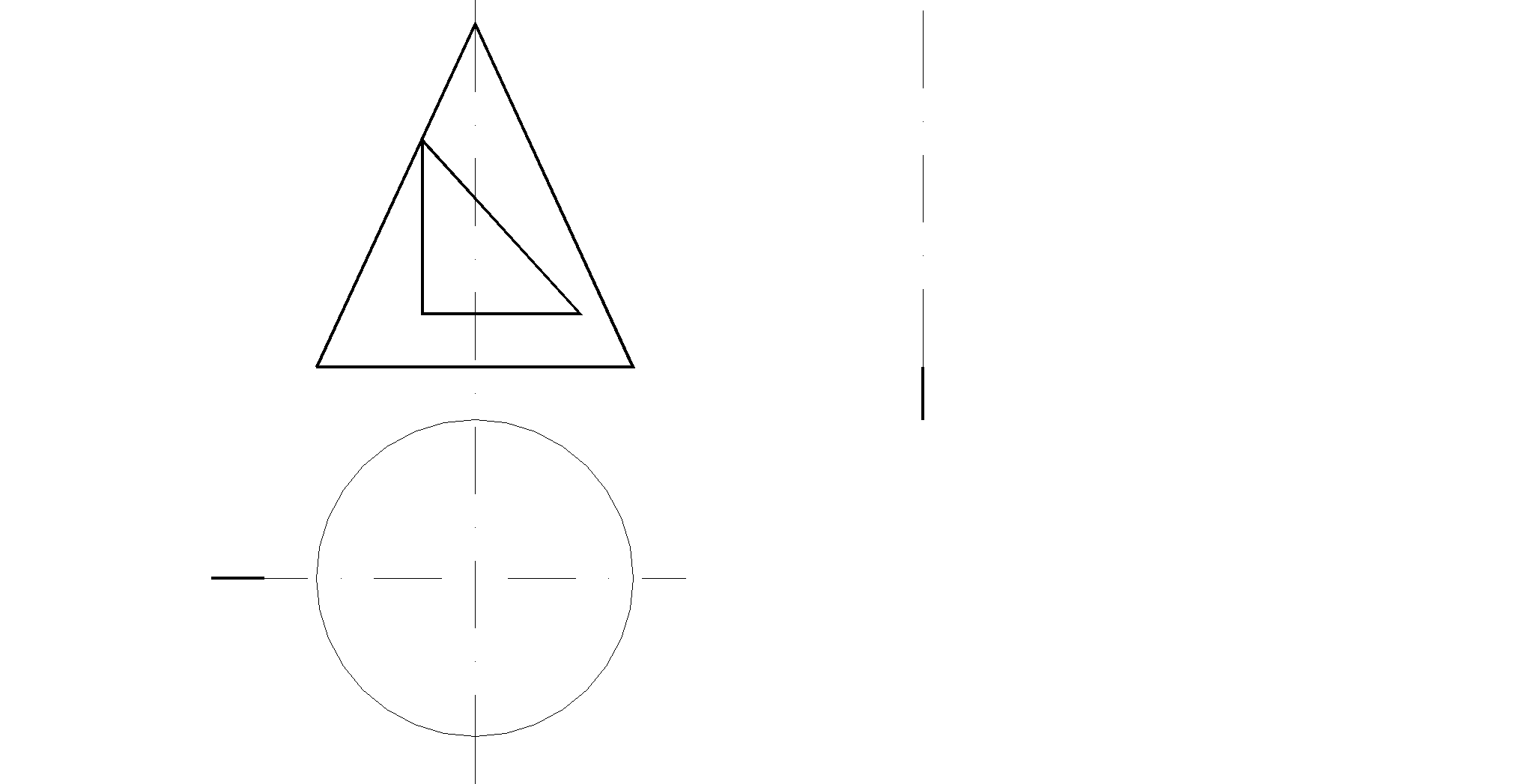
60. Построить проекции точек пересечения прямых h, i, l c поверхностью
l2
конуса.
i2
h2
h1
i1
l1
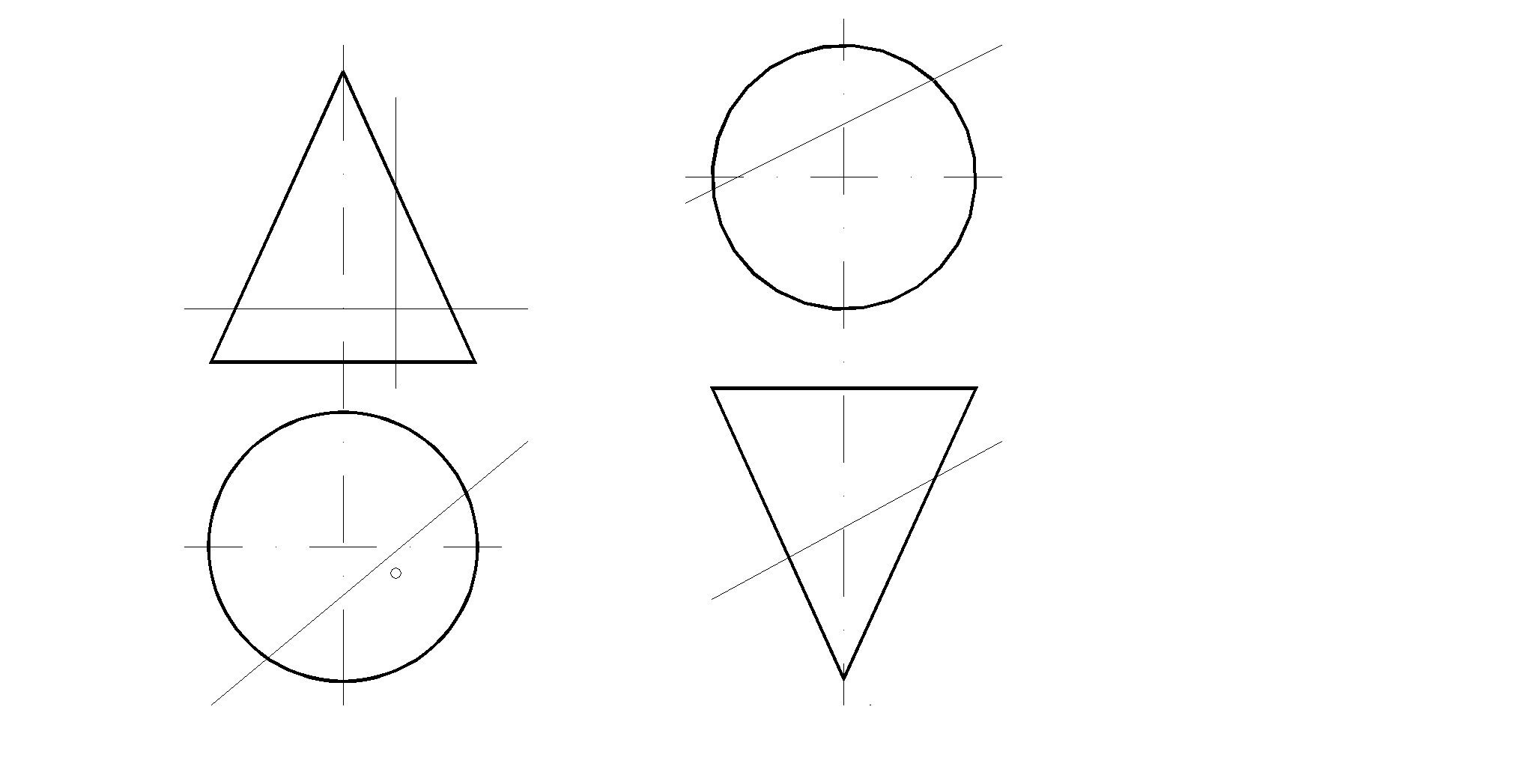
61. Построить недостающие проекции точек и линии на поверхности сферы.
62. Построить три проекции сферы с вырезом.
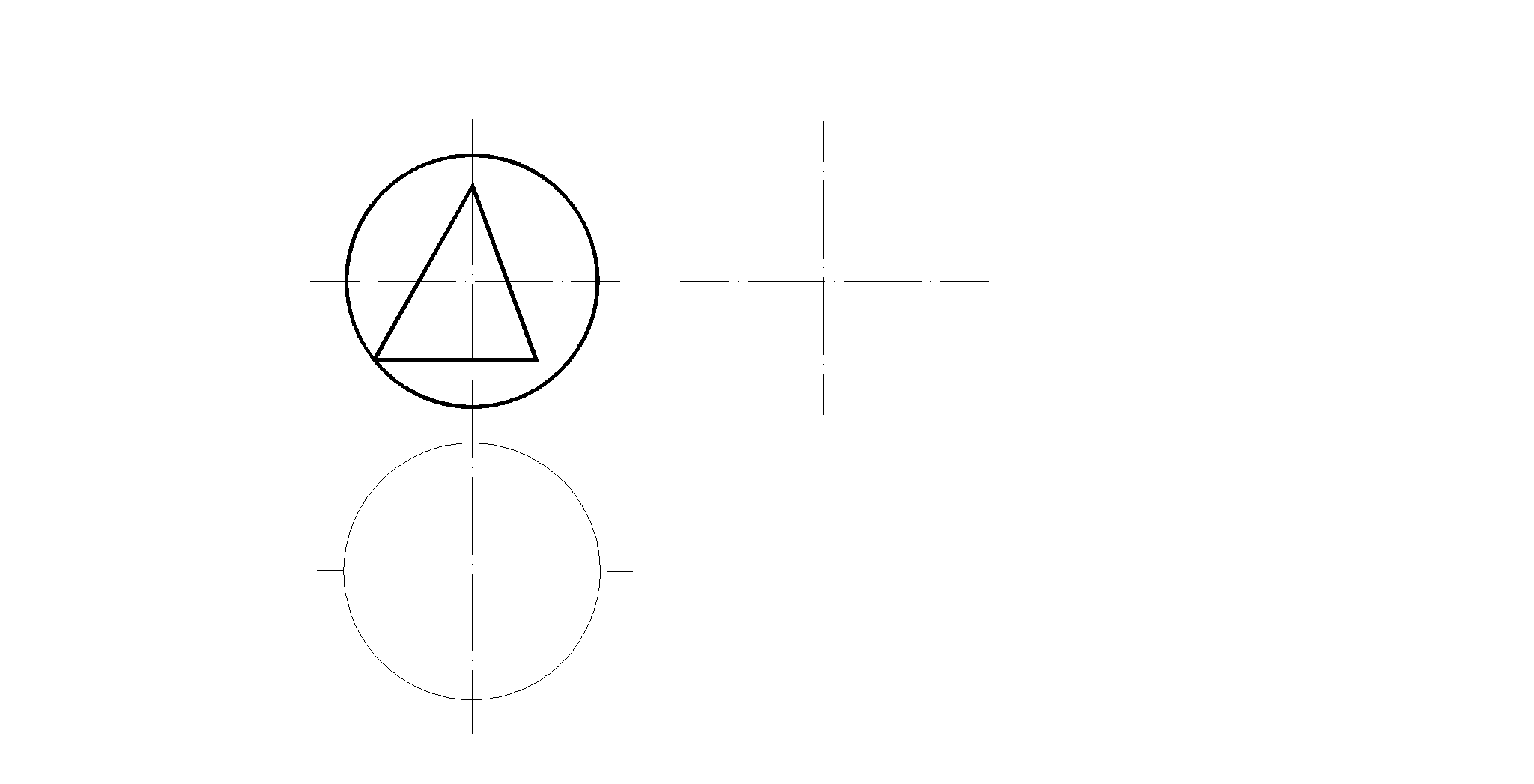
63. Построить проекции точек пересечения сферы с прямыми f и i. Определить видимость прямых.
f2
a)
б)

f1
i2
i1
64. Построить проекции точек пересечения тора с прямой m. Определить видимость прямой.
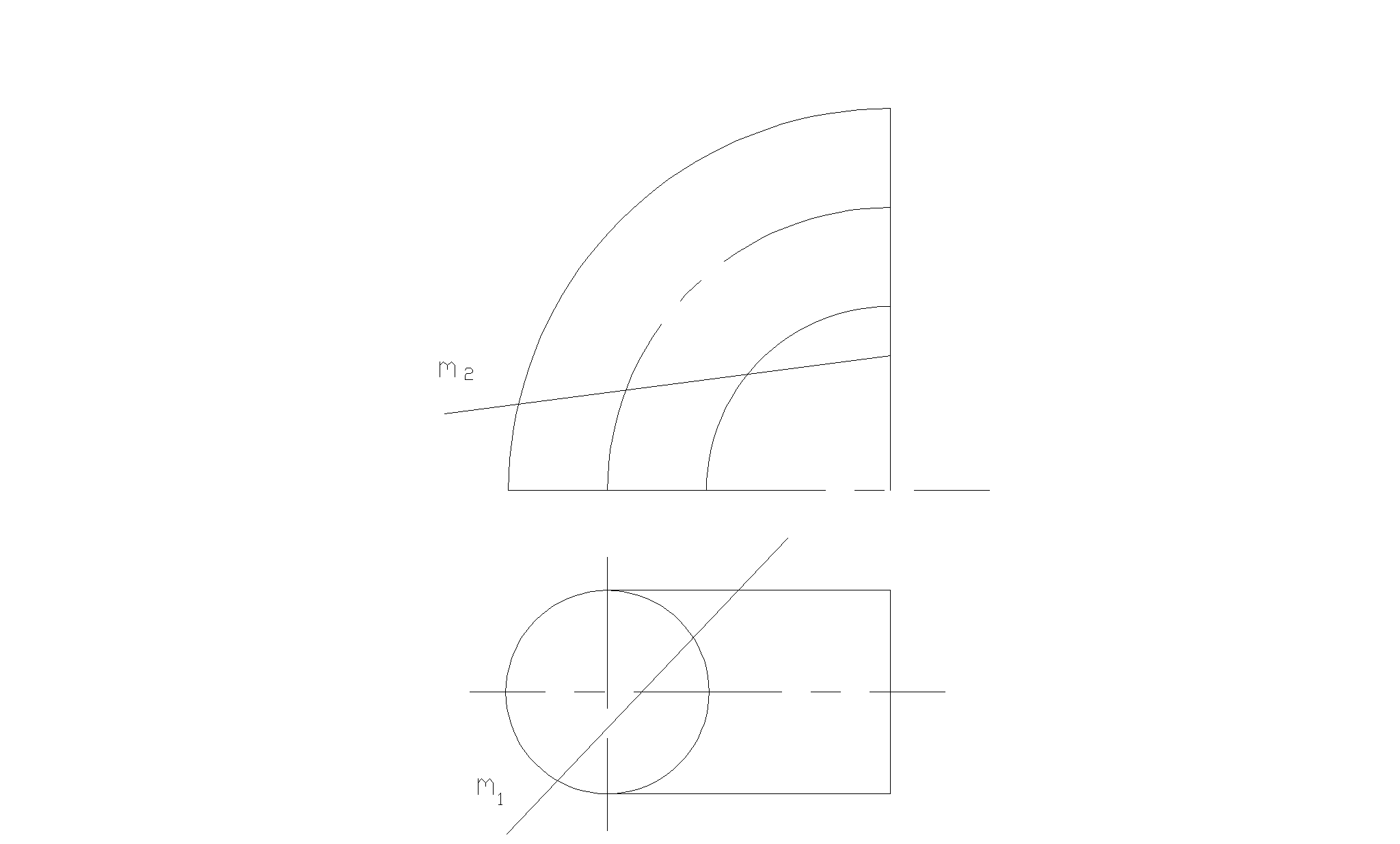
65. Построить три проекции тора с вырезом.
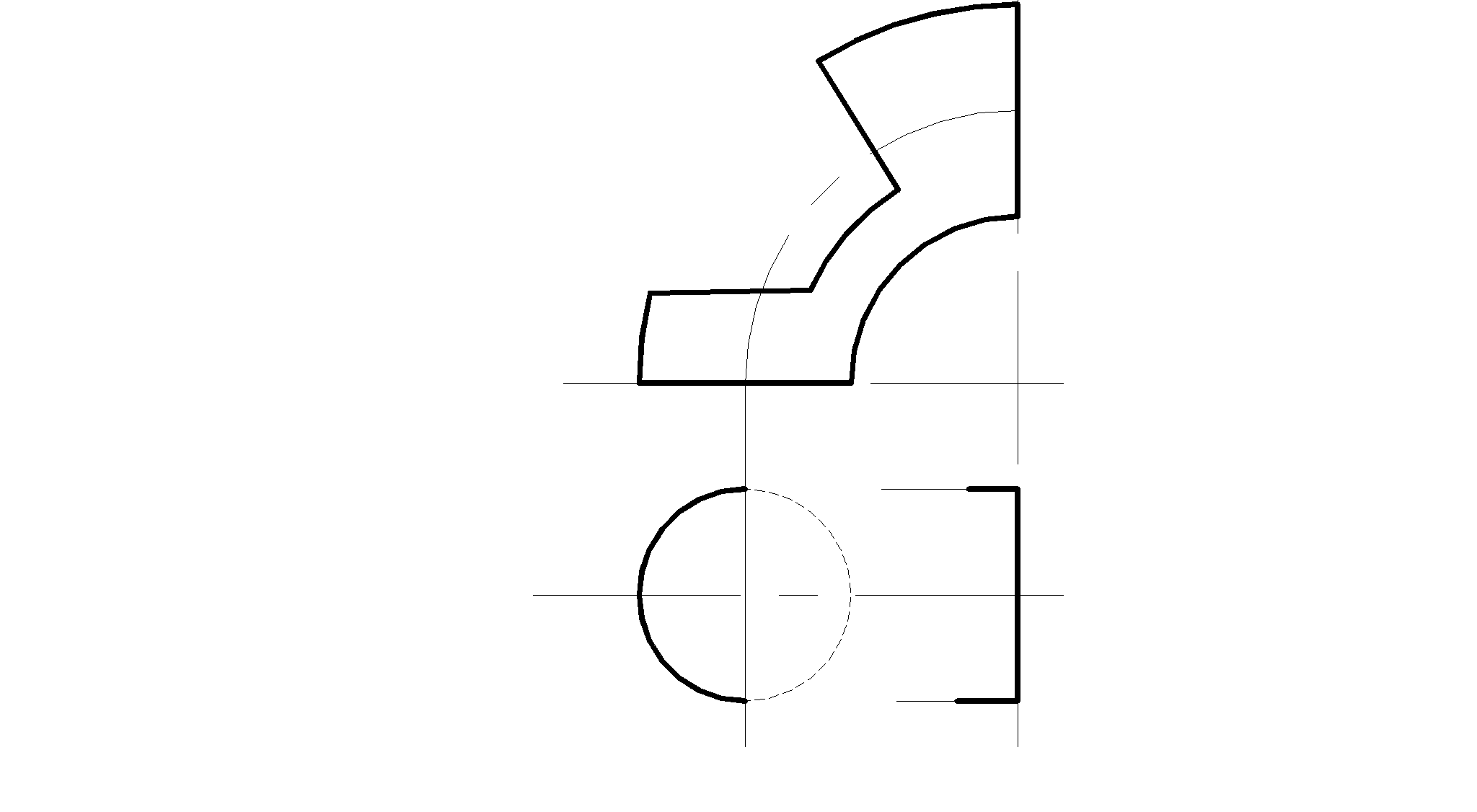
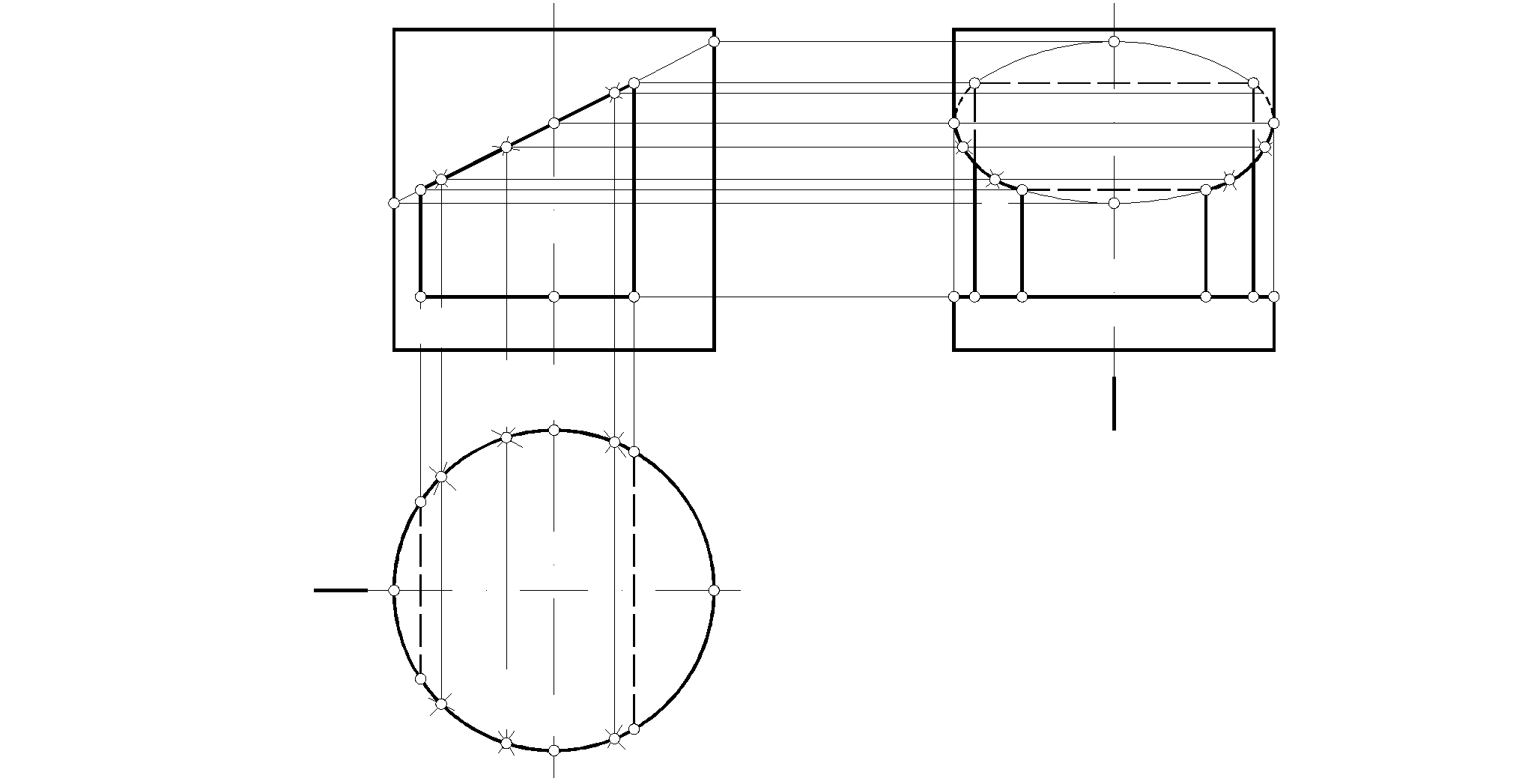
6.2 Примеры решения задач раздела 6
1. Построить три проекции цилиндра с вырезом
А2
C2(D2)
12 (22)
32(42)
52 (62)
72(82)
92 (102)
А3
13
23
D3
C3
(43)
(33)
83
73
(63)
(53)
103
93
Ф3
Ф1
(А1)
(В1)
(31)(51)
(41)(61)
(11)(91)
(21)(101)
(D1)(81)
(C1)(71)
2. Построить три проекции конуса с вырезом
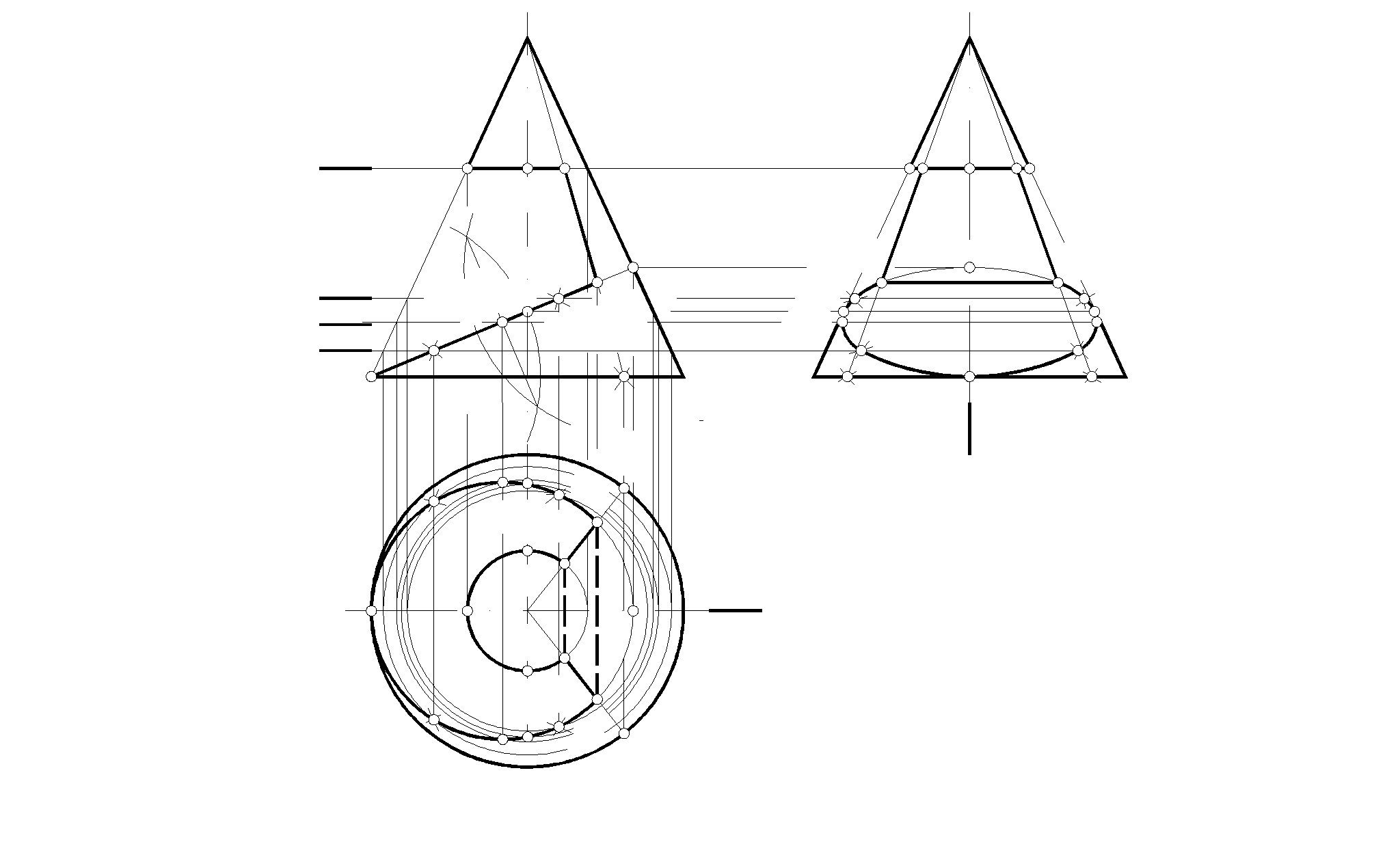 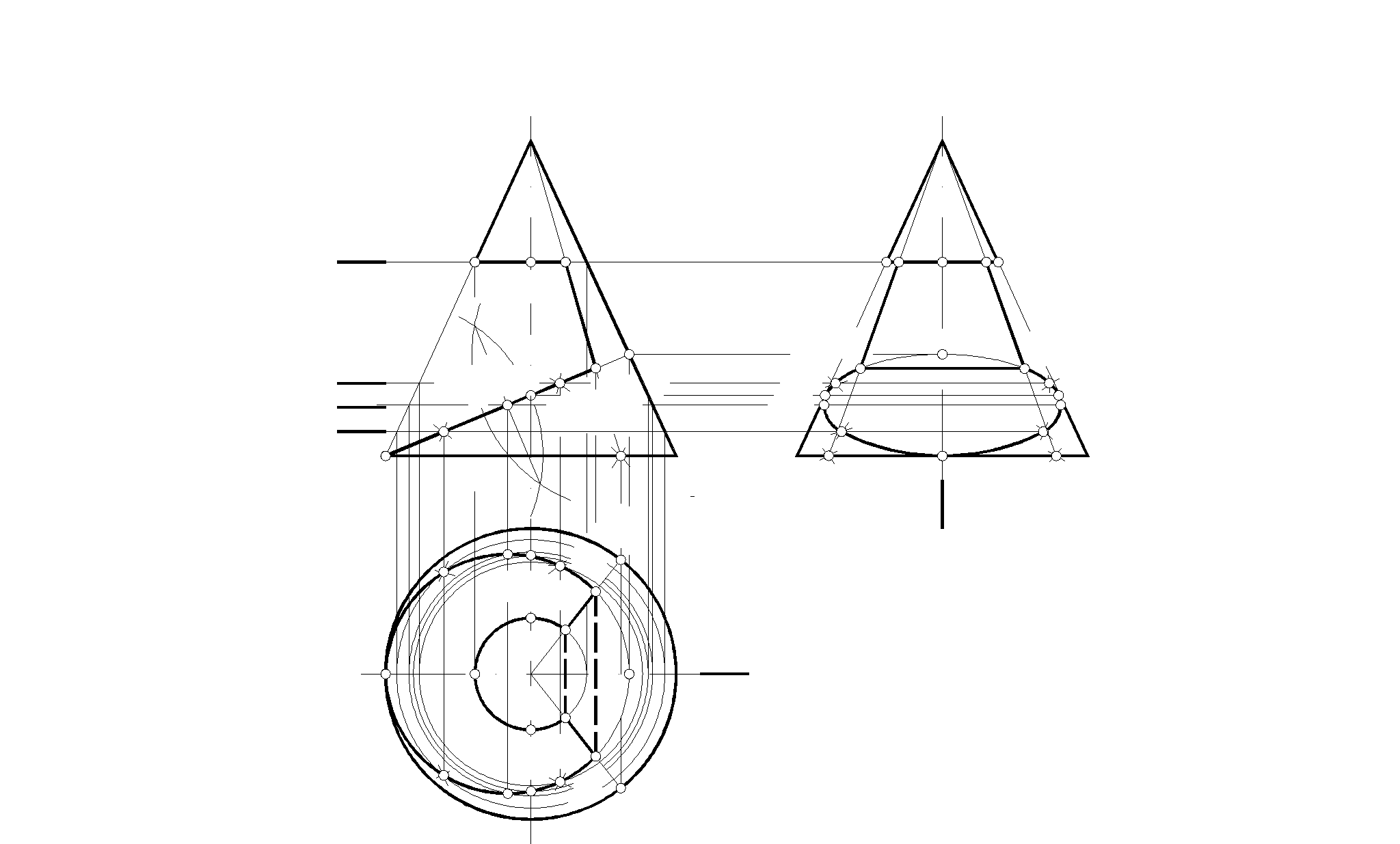
(42)(52)
(22)(32)
33
(С2)(D2)
(62)(72)
(82)(92)
23
13
(53)
12
(В3)
А3
A1
91
D1
71
B1
61
81
В2
C1
11
7 ПЕРЕСЕЧЕНИЕ ПОВЕРХНОСТЕЙ
7
.1 Задачи к разделу 7
Сформулируйте правило построения линии взаимного пересечения поверхностей многогранников.
Что представляет собой линия взаимного пересечения поверхностей многогранников в случаях:
все ребра одного многогранника пересекаются с гранями другого?
не все ребра одного многогранника пересекаются с гранями другого?
Сформулируйте правило построения линии пересечения многогранника с поверхностью вращения.
Что представляет собой линия пересечения многогранника с поверхностью вращения? Сформулируйте правило построения линии взаимного пересечения поверхностей вращения.
Как выбрать вспомогательные плоскости при построении линии пересечения:
двух конусов?
двух цилиндров?
конуса и цилиндра?
Что представляет собой линия взаимного пересечения поверхностей вращения в случаях:
все образующие одной поверхности пересекаются с другой поверхностью?
не все образующие одной поверхности пересекаются с другой поверхностью?
В чем заключается сущность метода вспомогательных сфер?
В каких случаях для построения линии пересечения поверхностей применяется метод вспомогательных сфер?
Частные случаи пересечения поверхностей вращения. Теорема Монжа.
________________________________________________________________
66. Построить проекции линии пересечения двух поверхностей.
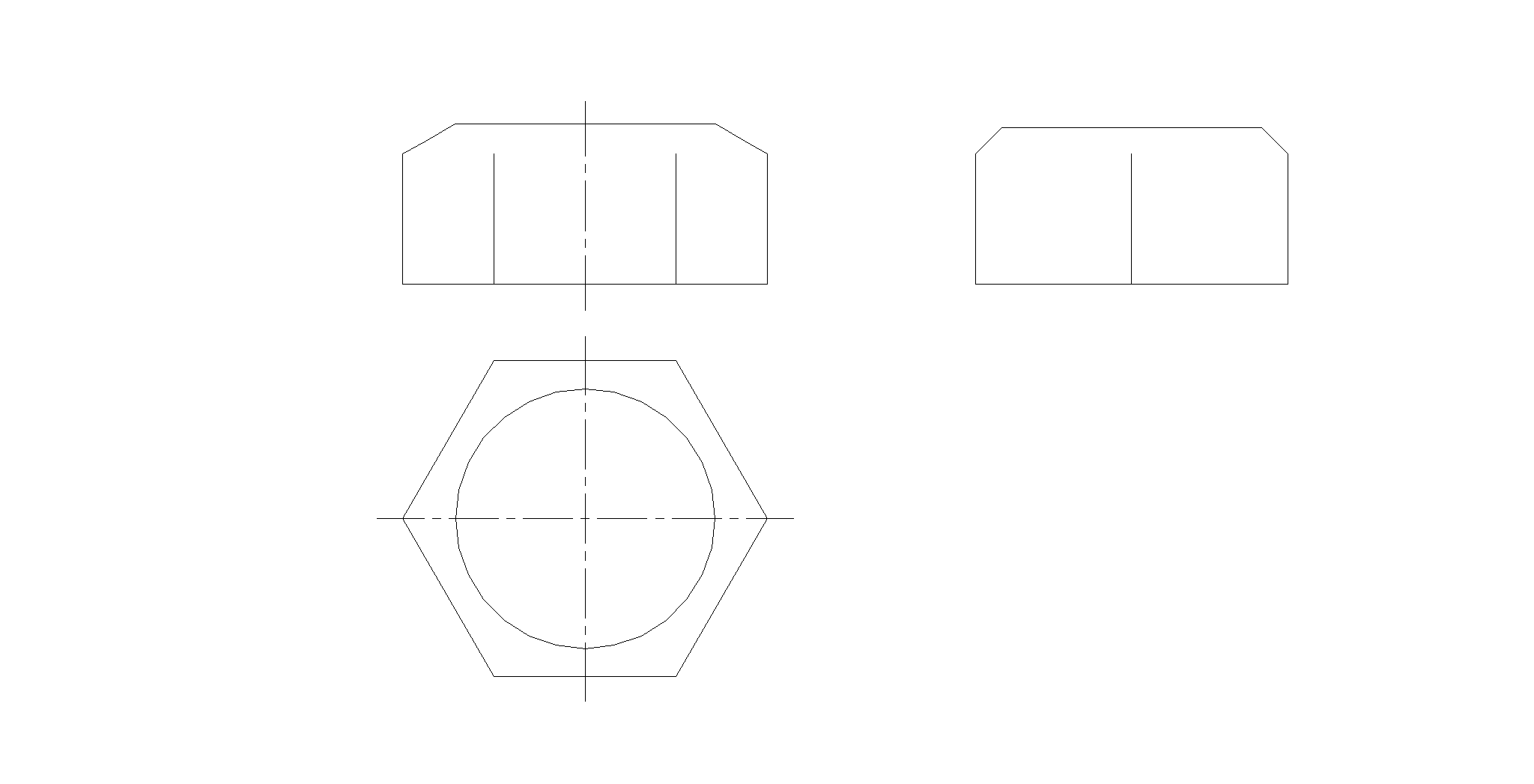
Построить проекции линии пересечения поверхностей
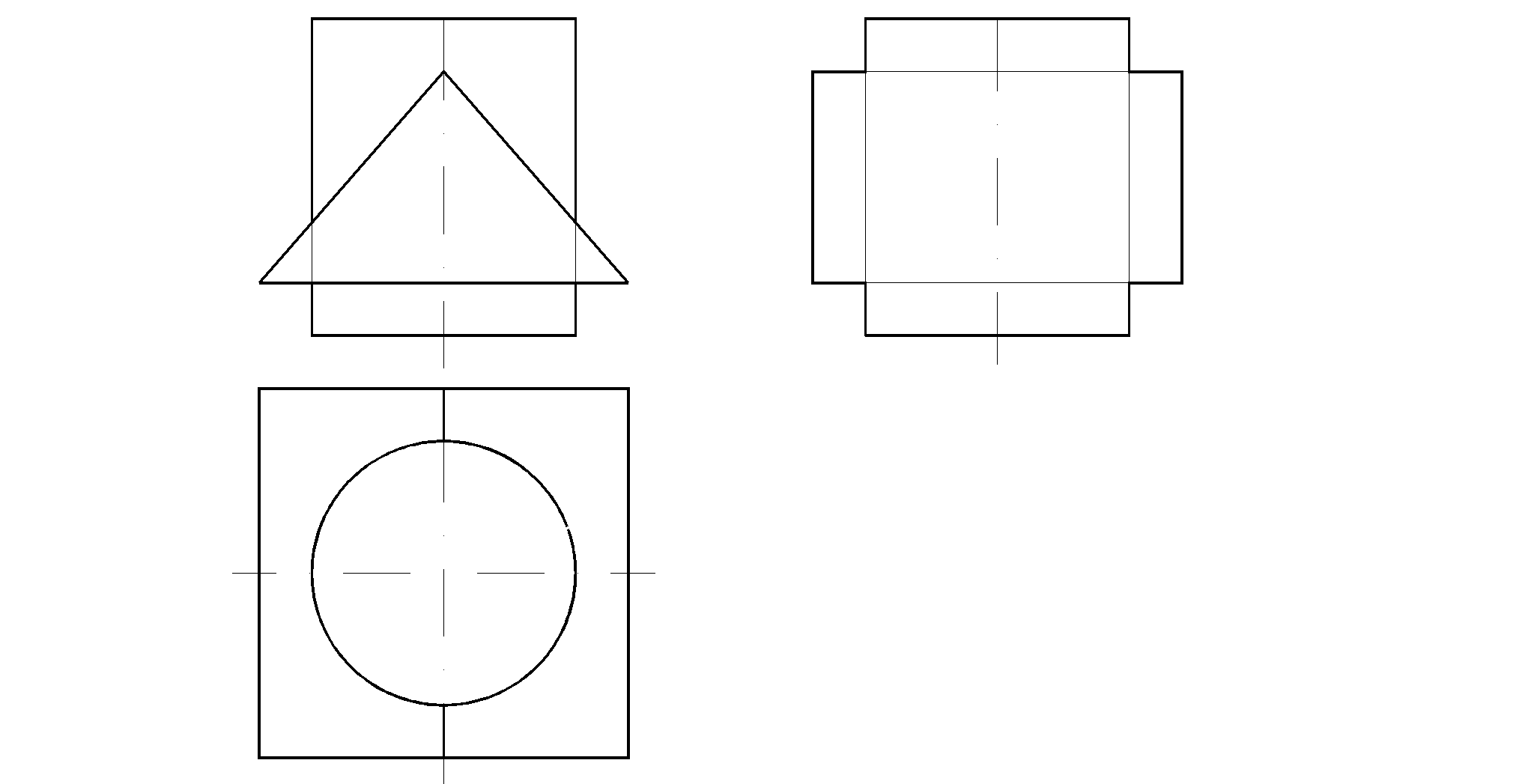
67.
68. 
69. Построить проекции линии пересечения поверхностей
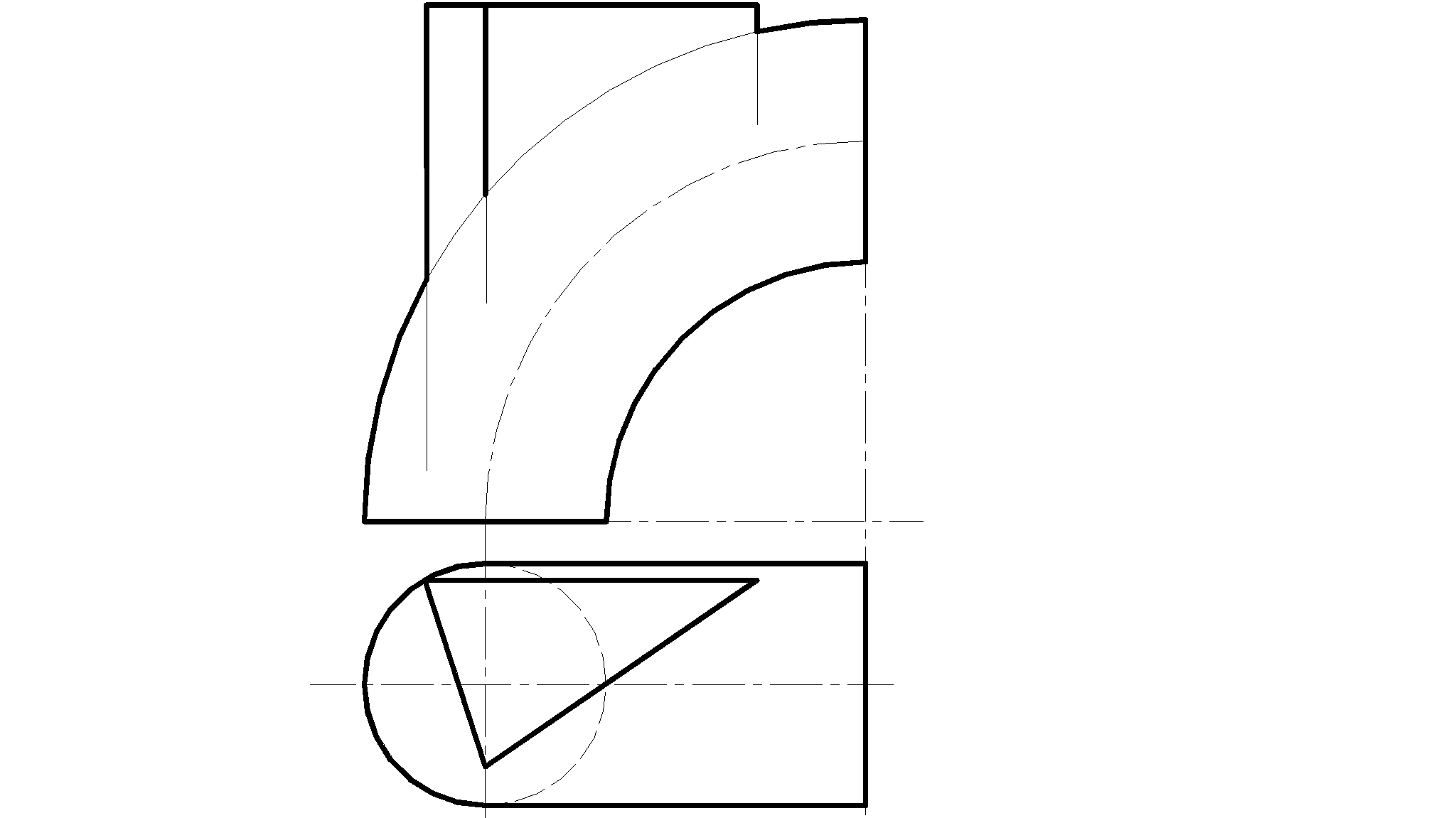
70. Построить проекции линии пересечения поверхностей
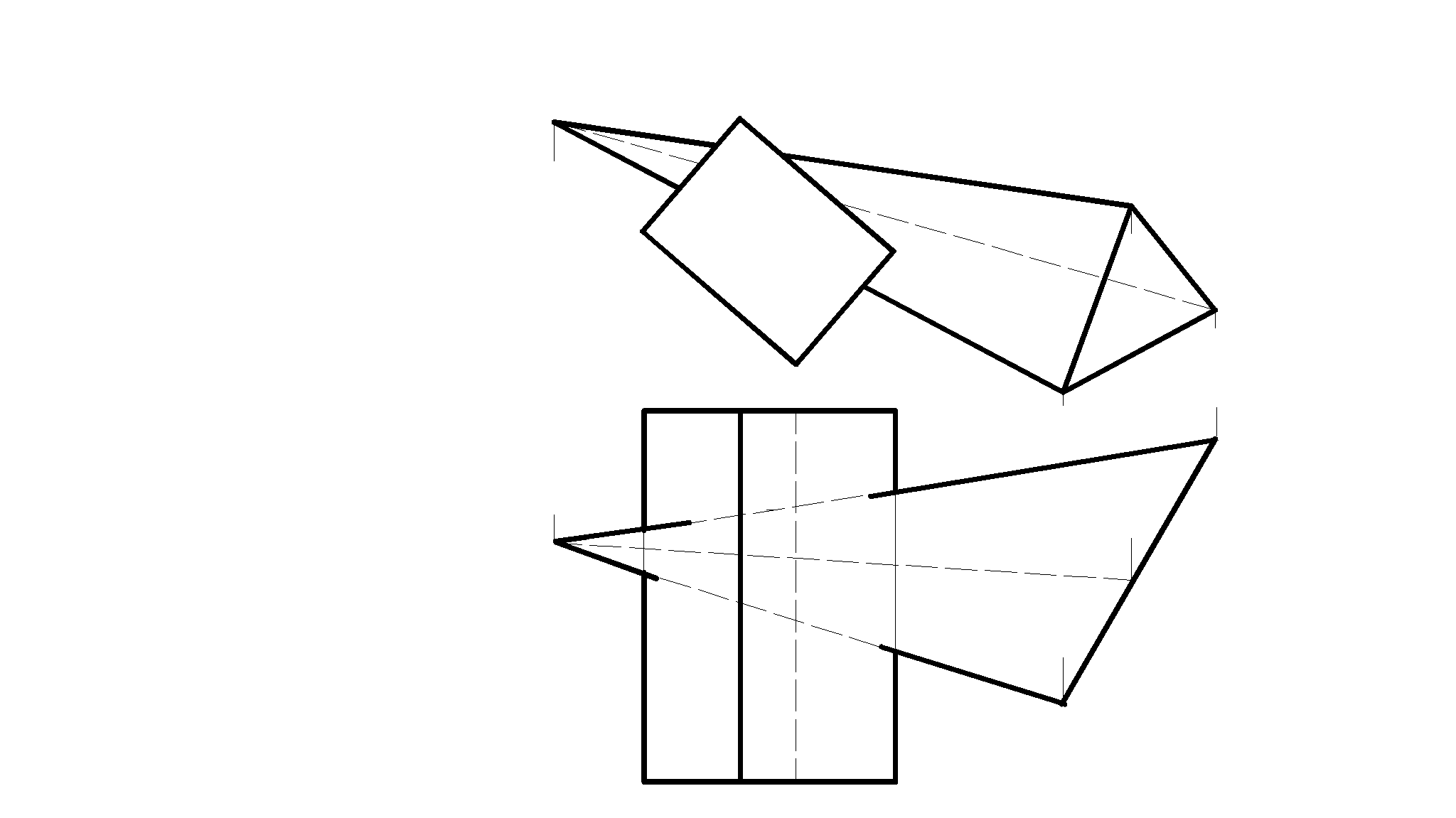
71. Построить проекции линии пересечения поверхностей
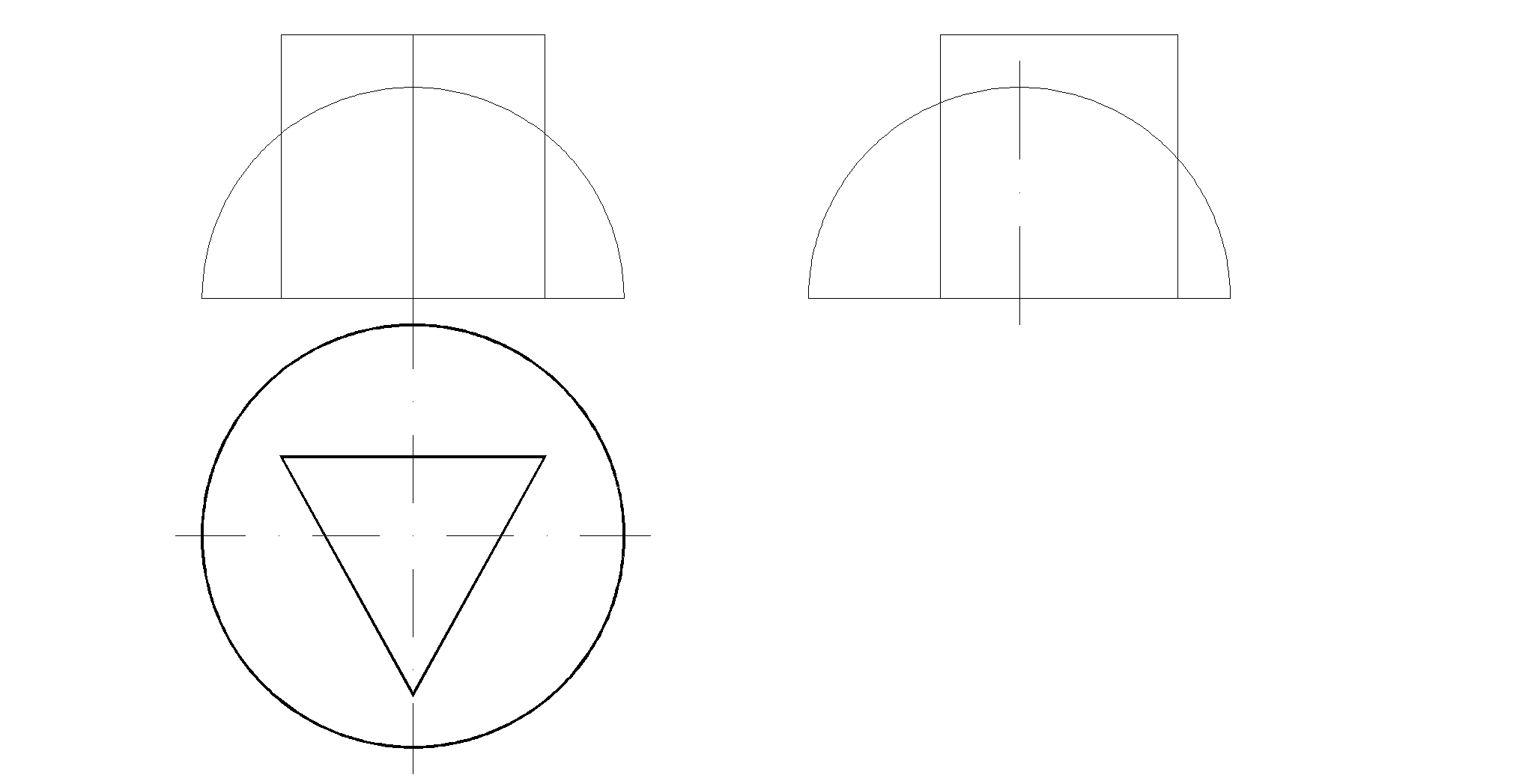
72. Построить проекции линии пересечения поверхностей
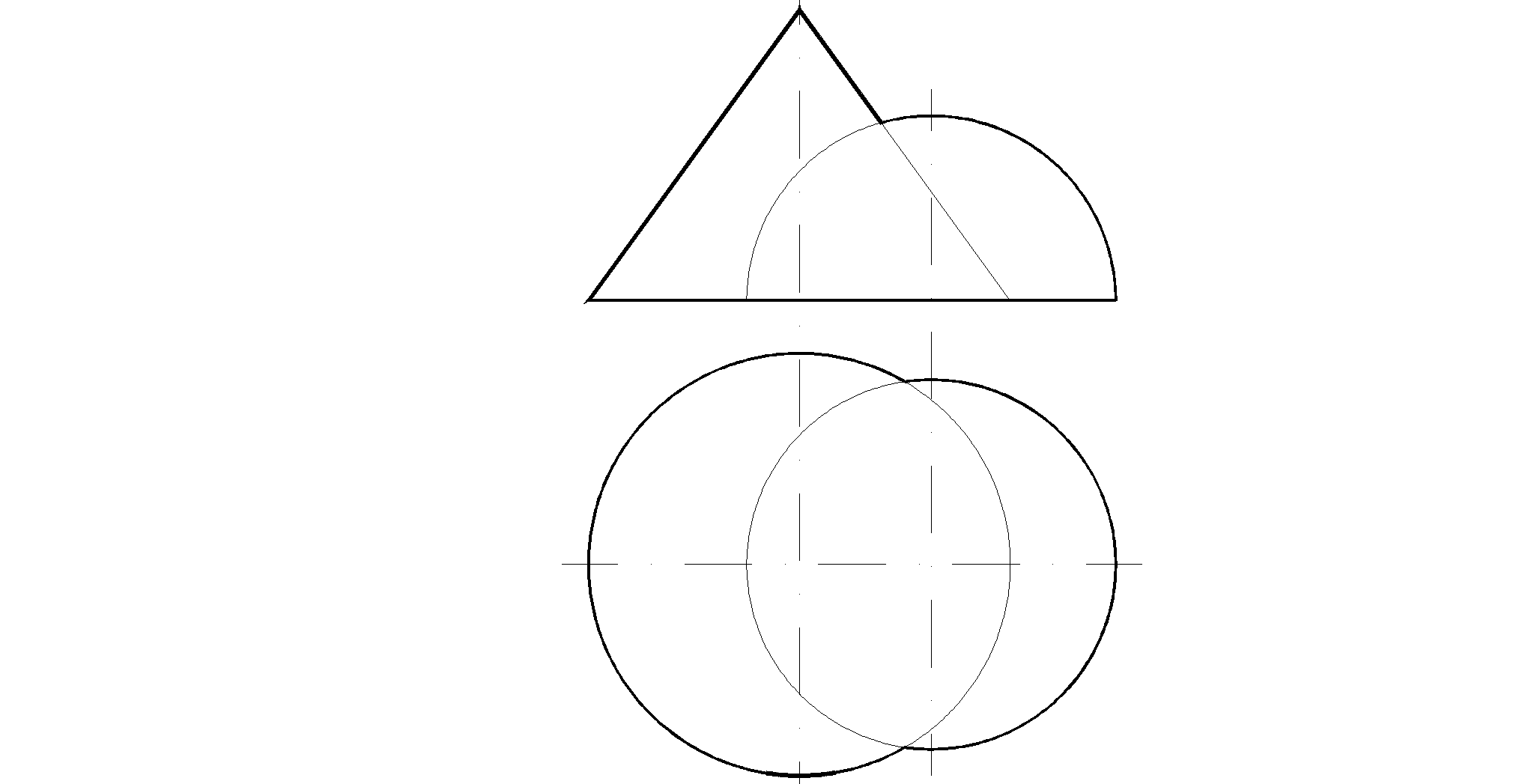
73. Построить проекции линии пересечения поверхностей
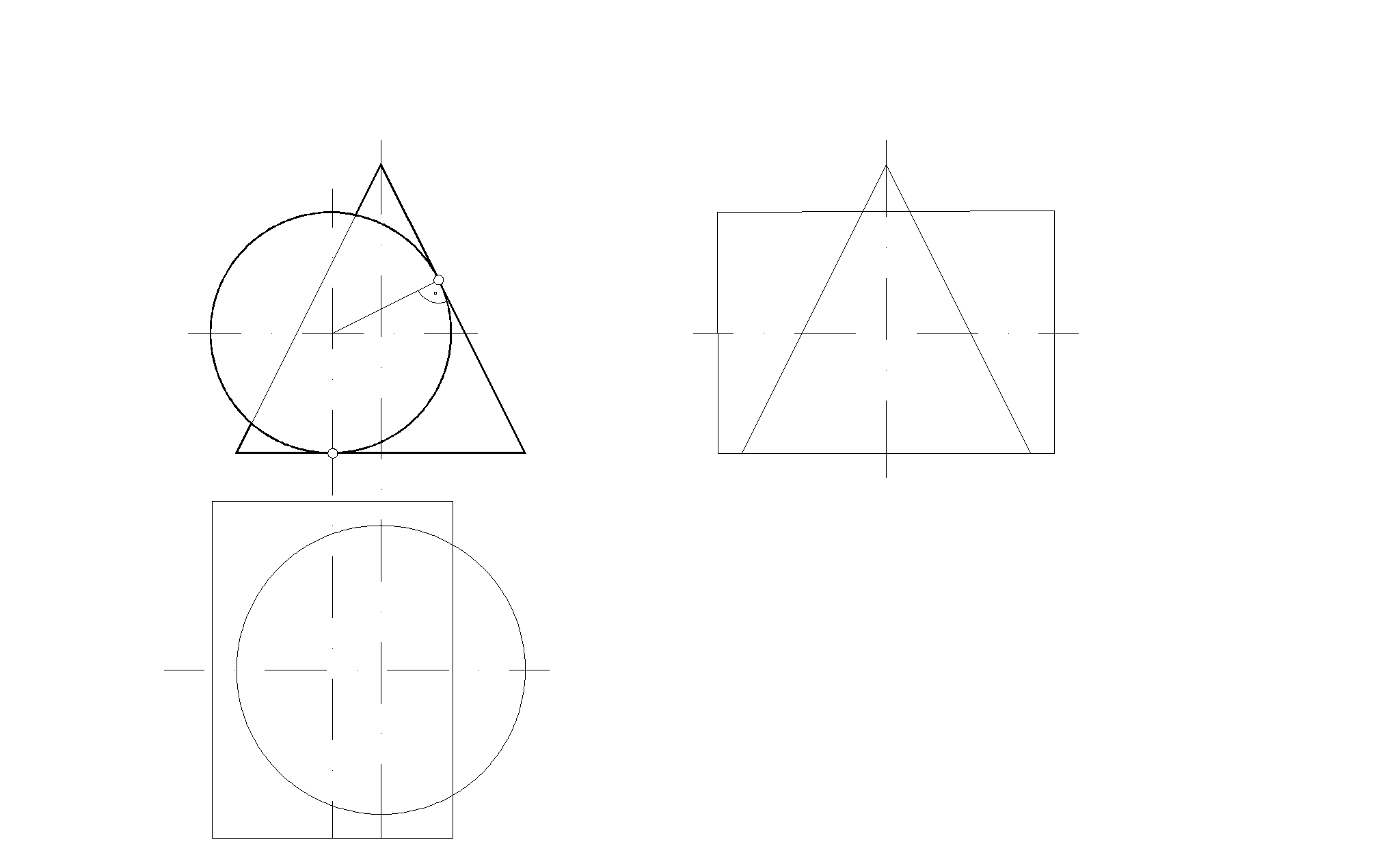
74. Построить проекции линии пересечения поверхностей
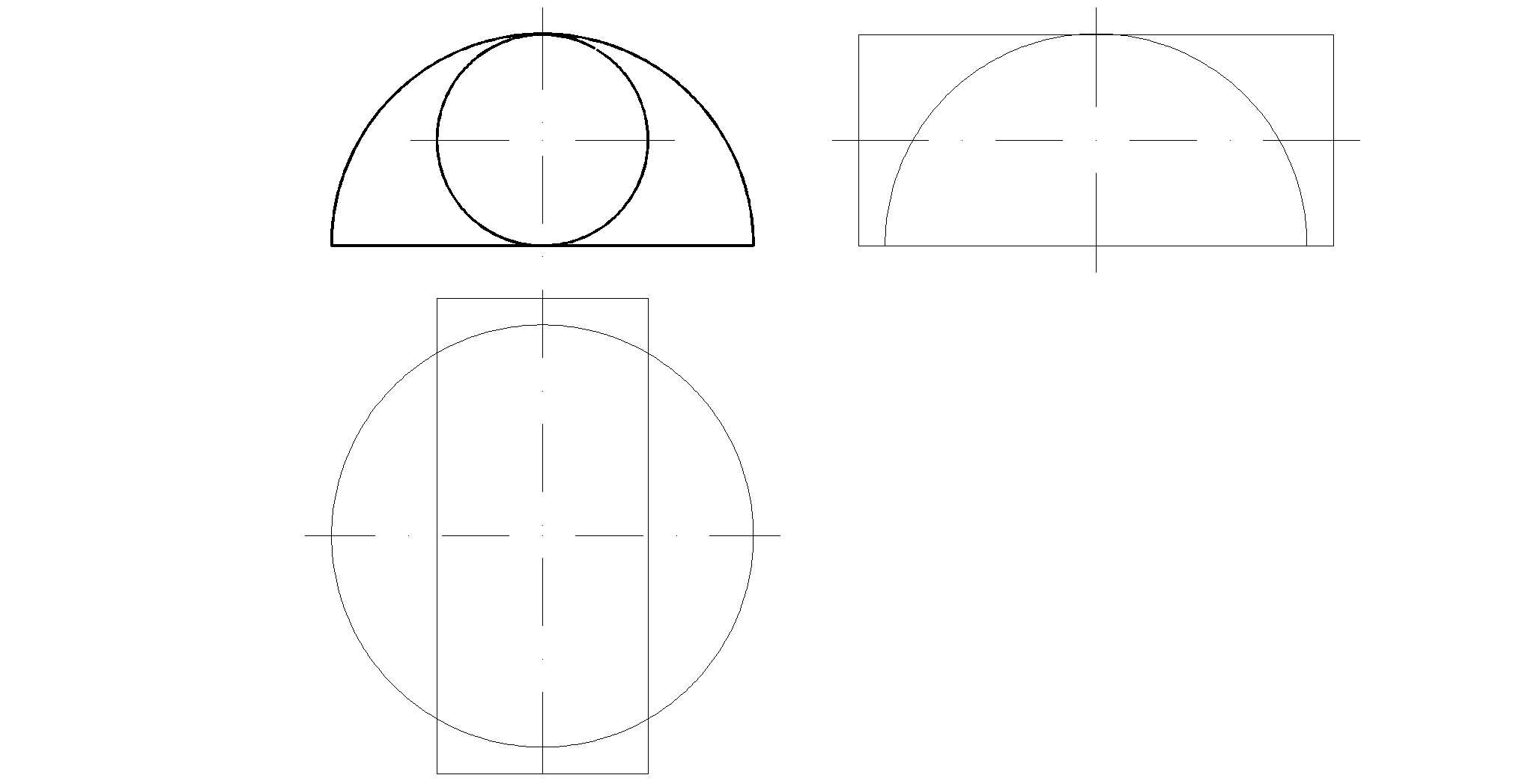
75. Построить проекции линии пересечения поверхностей.
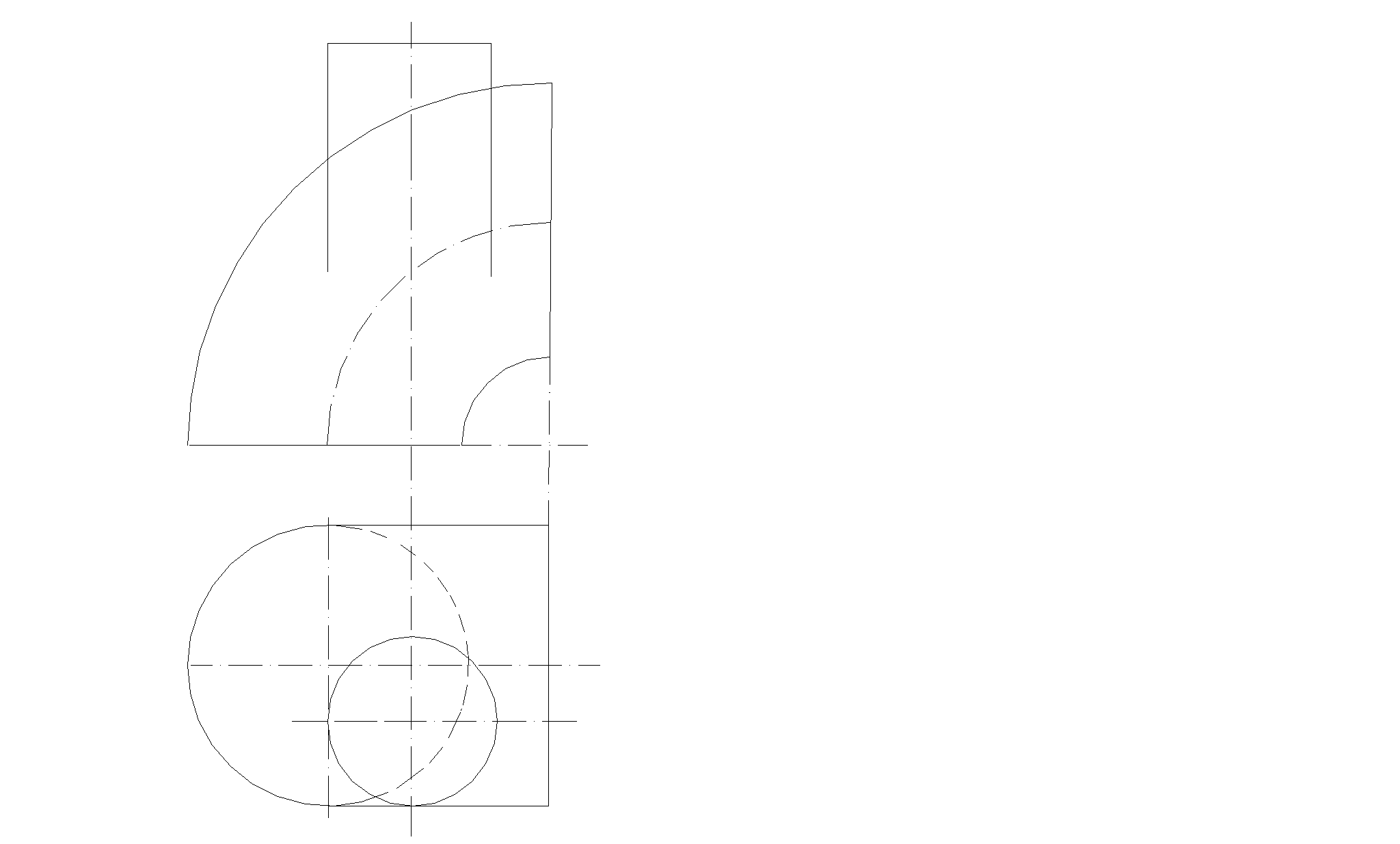
76. Построить проекции линии пересечения.
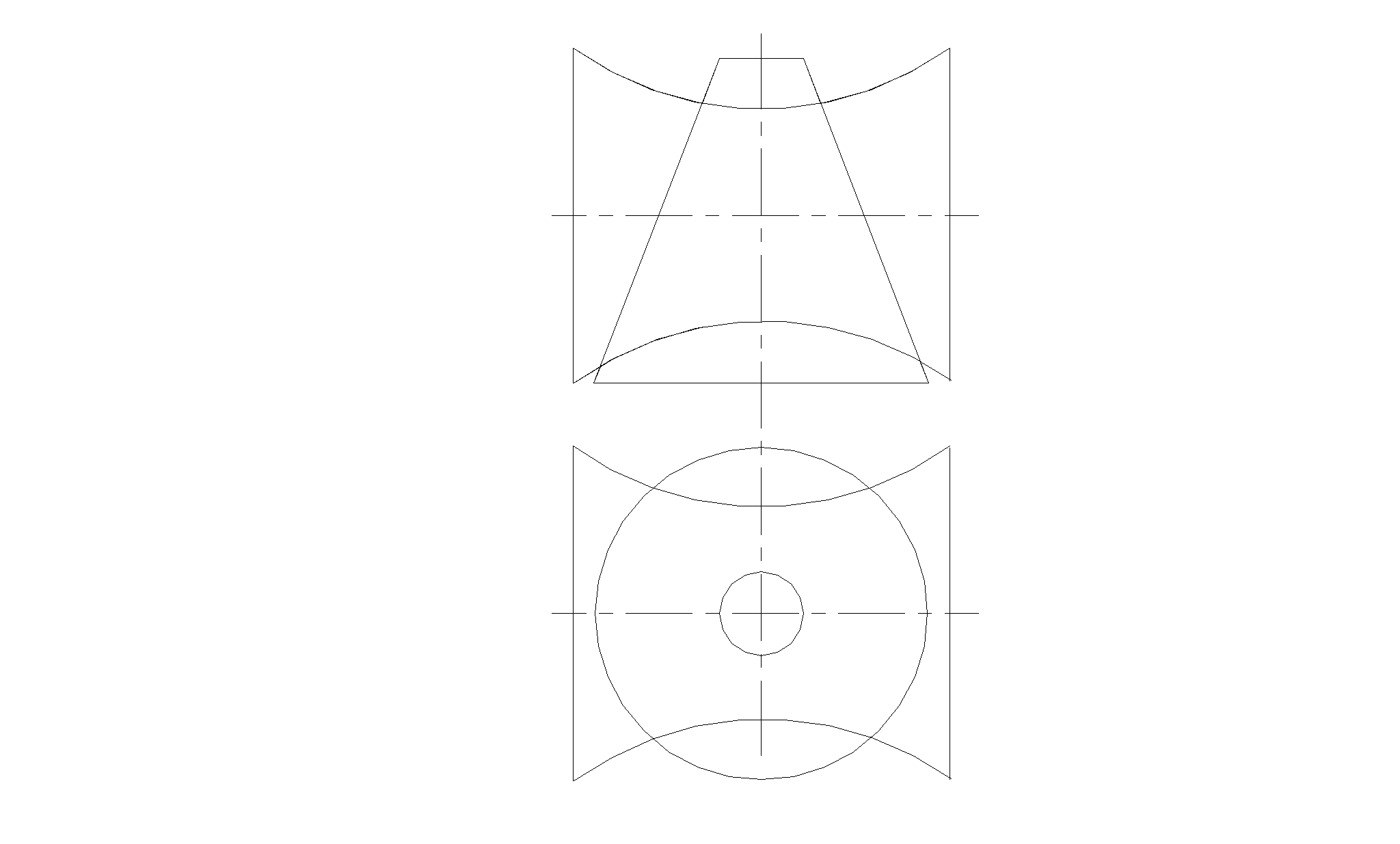
77. Построить проекции линии пересечения наклонного конуса и прямого кругового цилиндра (теорема Монжа).

78. Построить проекции линии пересечения поверхностей
(теорема Монжа)
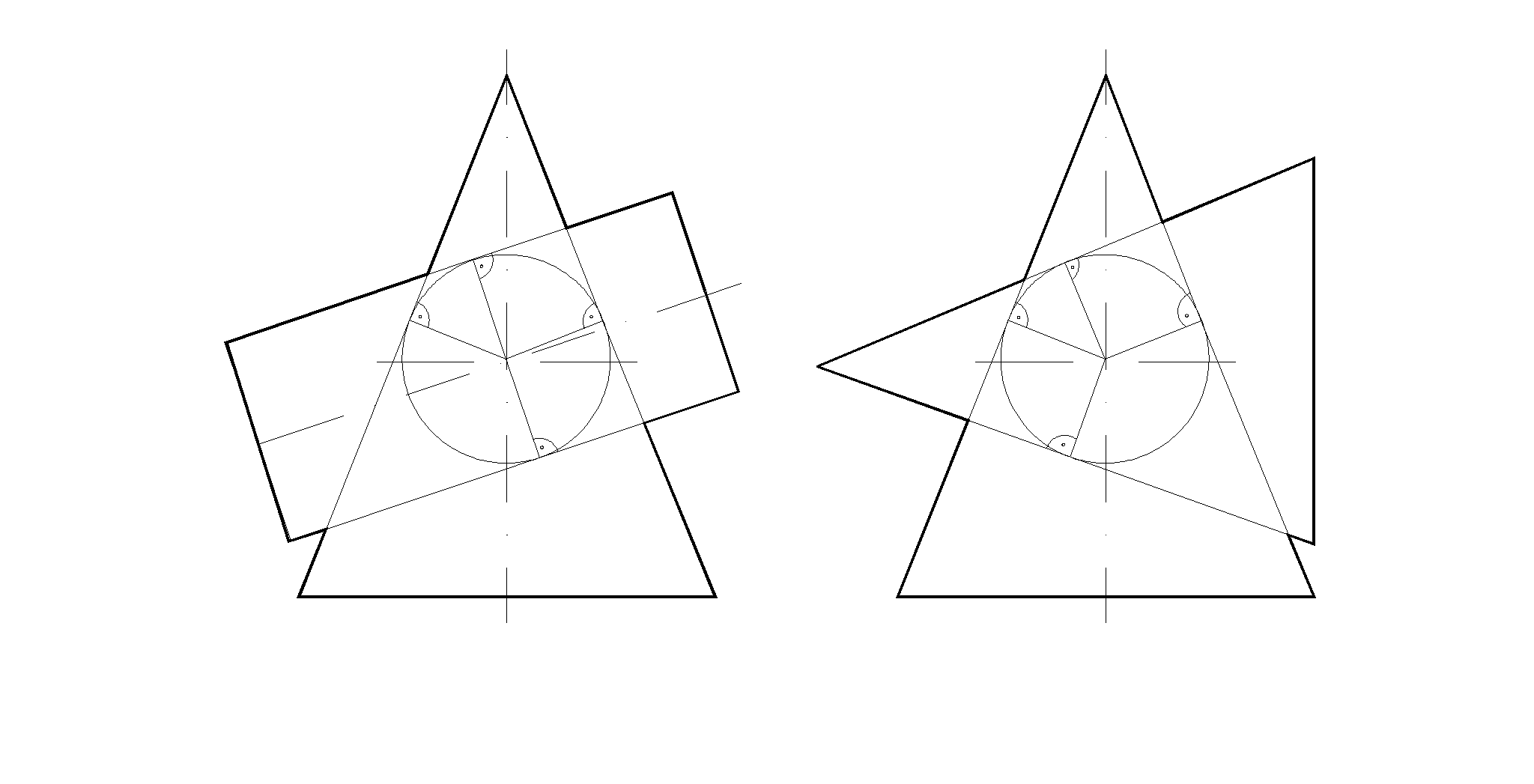
79. Построить проекции линии пересечения поверхностей (метод сфер)
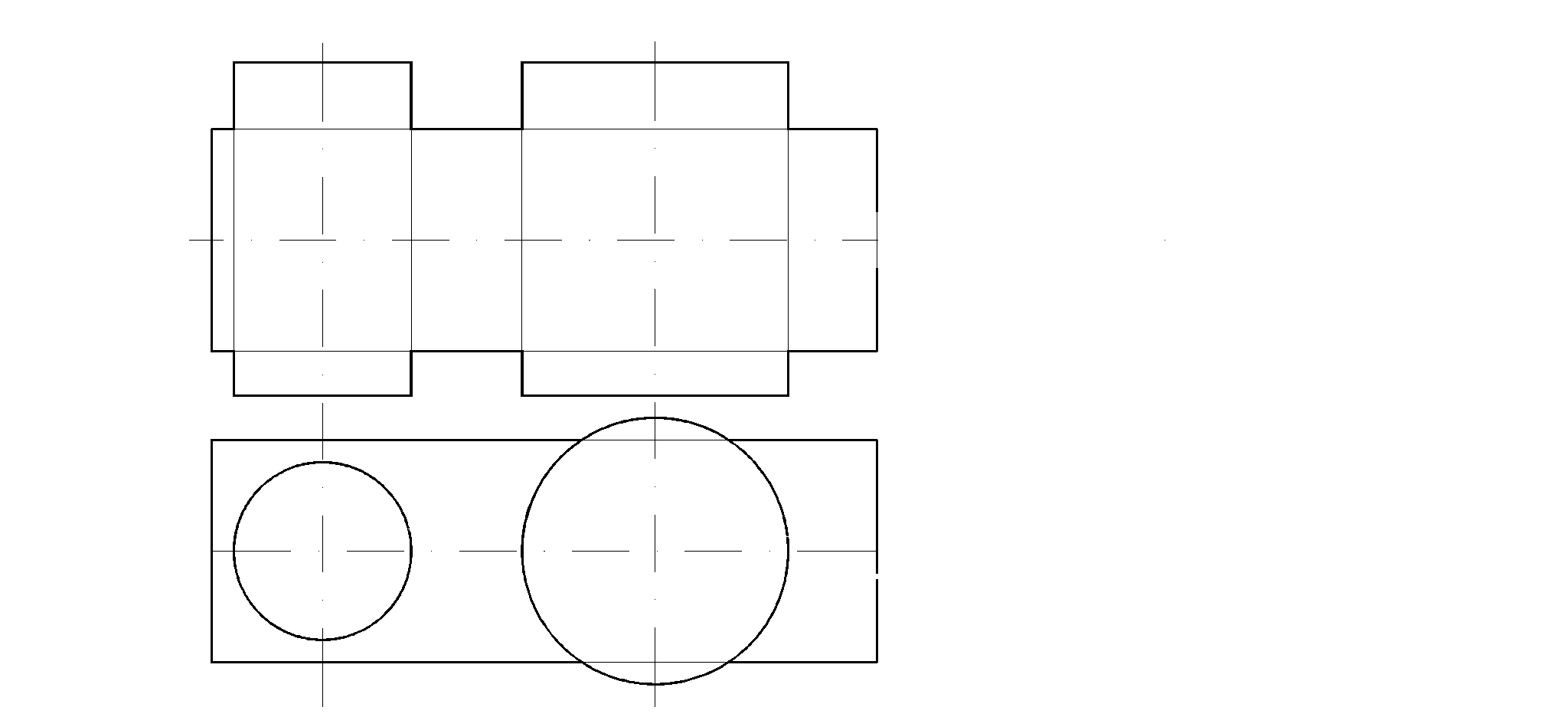
80. Построить проекции линии пересечения поверхностей (метод сфер)
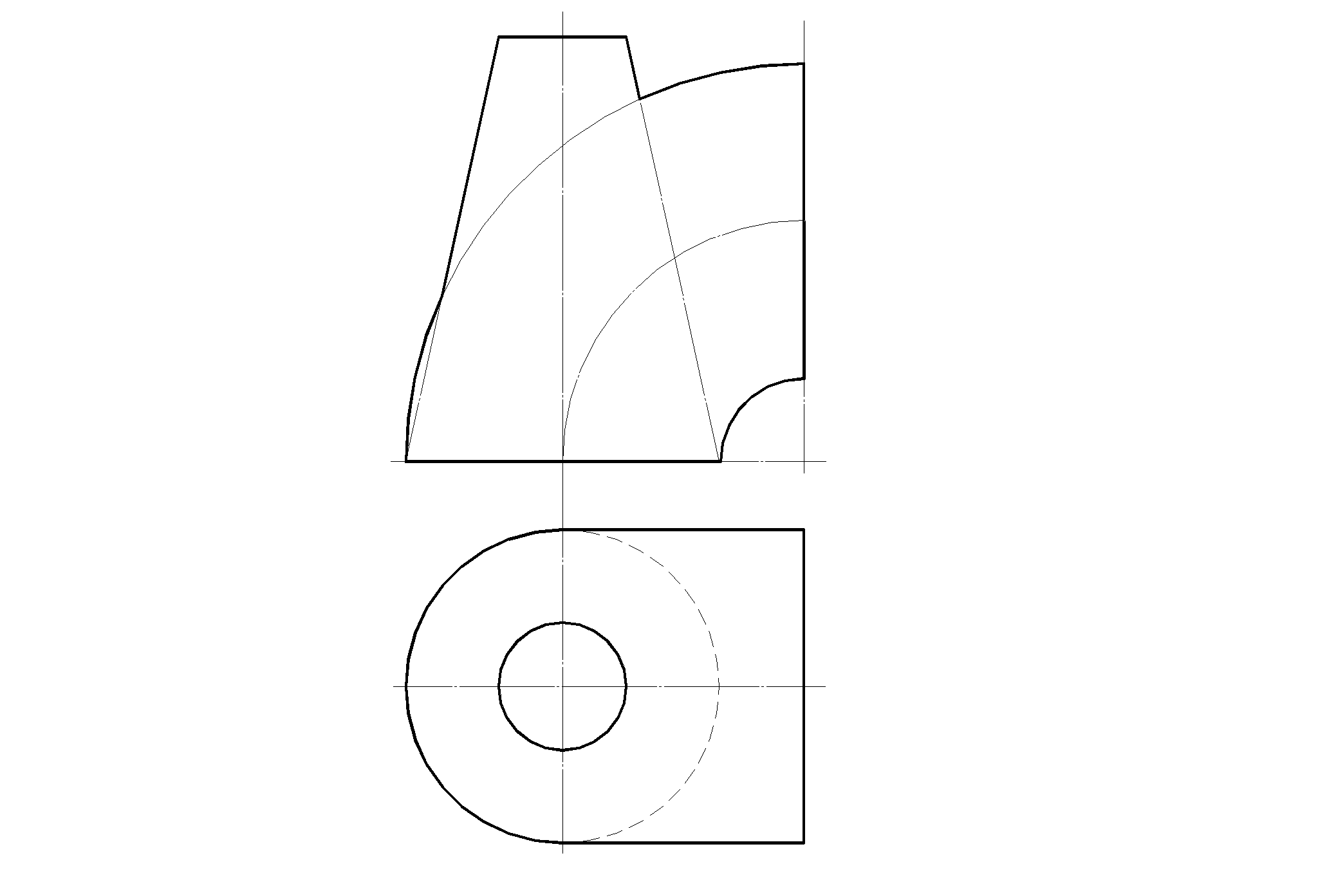
7.2 Примеры решения задач раздела 7
1. Построить проекции линии пересечения призмы с конусо
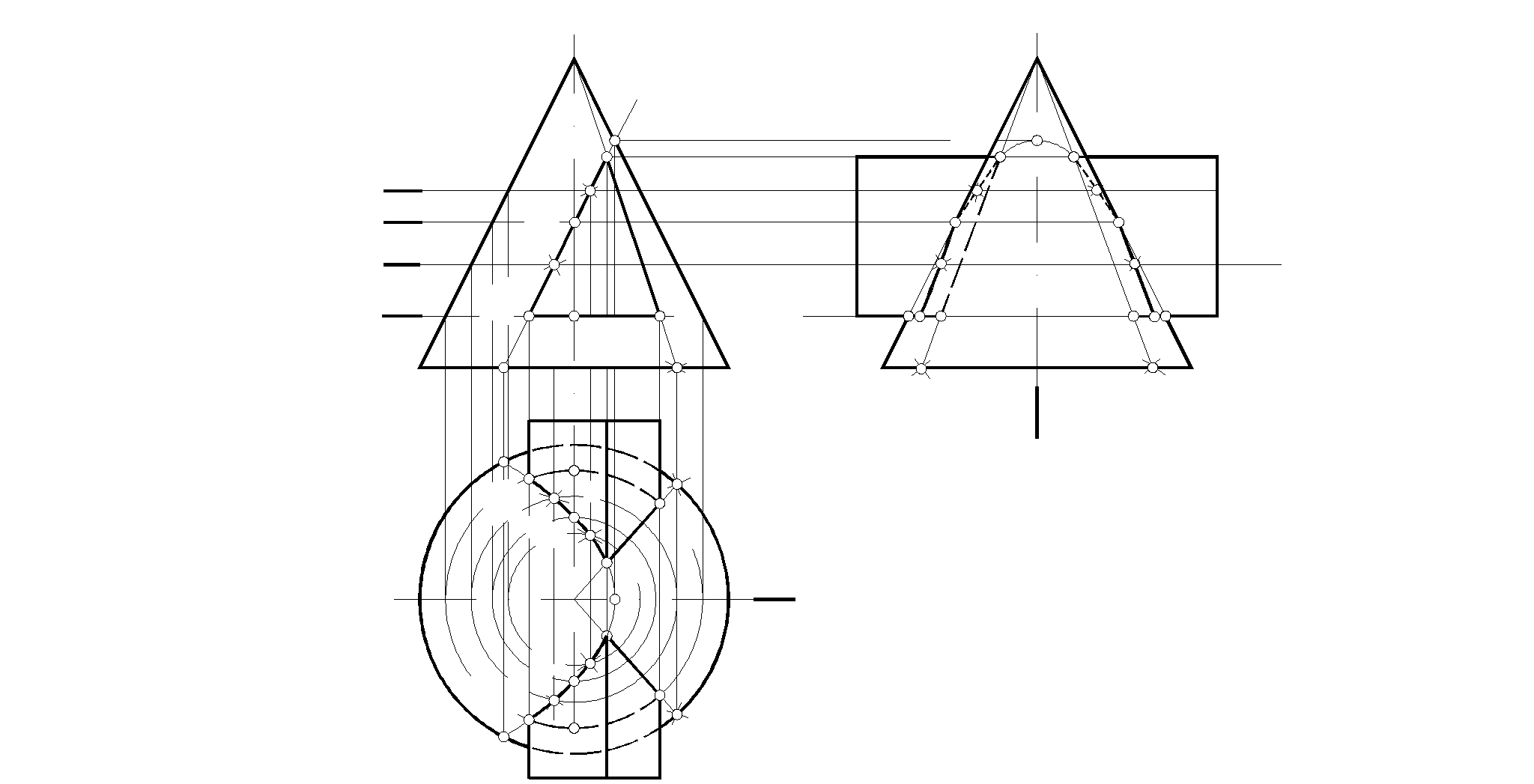
Г2
Г2
12(22)
32 (42)
52 (62)
72(82)
92(102)
21
41
61
51
81
(101)
(91)
11
31
71
103
(83)
43
23
(63)
(53)
33
93
13
(73)
Ф3
Ф1
Г2
Г2
12(22)
32 (42)
52 (62)
72(82)
92(102)
21
41
61
51
81
(101)
(91)
11
31
71
103
(83)
43
23
(63)
(53)
33
93
13
(73)
Ф3
Ф1
2
12
62 (72)
13
63
73
(71)
111
(41)
(81)
Ф3
. Построить линию пересечения цилиндра со сферой 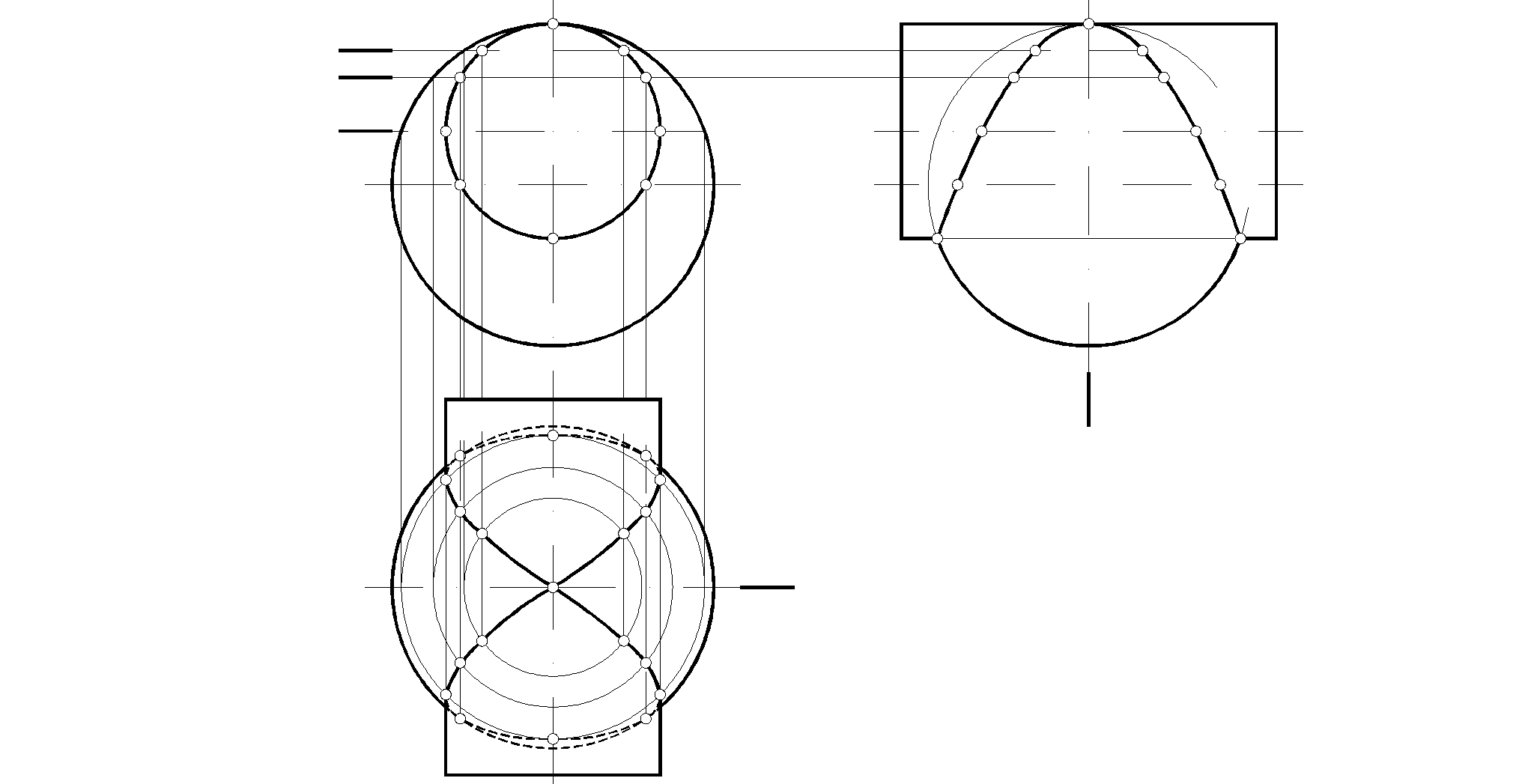
Г2
Г2
22 (32)
42 (52)
82(92)
102(112)
103 (23)
83 (43)
93(53)
113(33)
(61)
(51)
(91)
31
11
21
101
Ф1
Библиографический список
Боголюбов, С. К. Инженерная графика [Текст] : учеб. – 3-е изд., испр. и доп. / С. К. Боголюбов. – М. : Машиностроение, 2000. – 352 с.
Гордон, В. О. Курс начертательной геометрии [Текст] : учеб. для вузов / В. О. Гордон, М. А. Семенцов-Огиевский. – М. : Наука, 1998. – 336 с.
Чекмарев, А.А. Инженерная графика / А.А. Чекмарев. - М.: Высшая школа, 2008.- 411с.
2 Лагерь А.И.Инженерная графика/ А.И. Лагерь - М.: Высшая школа, 2006.- 312с.
ПРИЛОЖЕНИЕ А
(справочное)
Перечень ключевых слов
Аксонометрия
- косоугольная
- прямоугольная
Алгоритм
База
- вспомогательная
- измерительная
- конструкторская
- основная
- промежуточная
- технологическая
Вершина
Взаимное расположение
Вид
- главный
- дополнительный
- местный
Видимость
Геометрия начертательная
Грань
Графика
ЕСКД
Комплексный чертежа
Конкурирующие точки
Контур
Конус круговой
Конусность
Кривые
Линии чертежа
Метод Монжа
Образующая
Овал
Окружность
Определитель поверхности
Ортогональное проецирование
Оси аксонометрические
|
Параллельное проецирование
Пересечение
Перпендикуляр
Пирамида
Пластина
Плоскость
Поверхность
Построения геометрические
Преобразование комплексного чертежа
Призма
Проекция
Проецирование
Пропорциональность
Пространственные представления
Прямая линия
Развертка
Сечение
Симметрия
Следы секущей плоскости
Способы задания
Стандарт
Сфера
Точка
Теорема Монжа
Центральное проецирование
Центр проецирования
Цилиндр круговой
Чертеж
Экватор
Эллипс
Эпюр
|
ПРИЛОЖЕНИЕ б
(справочное)
Образец шрифта ГОСТ 2.104-81
АаБбВвГгДдЕеЖжЗзИиКкЛлМмНнОоПпРрСсТтУуФфХхЦцЧчШшЩщЬьЪъЫыЭэЮюЯя
1 2 3 4 5 6 7 8 9 0
АаБбВвГгДдЕеЖжЗзИиКкЛлМмНнОоПпРрСсТтУуФфХхЦцЧчШшЩщЬьЪъЫыЭэЮюЯя
1 2 3 4 5 6 7 8 9 0
АаБбВвГгДдЕеЖжЗзИиКкЛлМмНнОоПпРрСсТтУуФфХхЦцЧчШшЩщЬьЪъЫыЭэЮюЯя
1 2 3 4 5 6 7 8 9 0
АаБбВвГгДдЕеЖжЗзИиКкЛлМмНнОоПпРрСсТтУуФфХхЦцЧч
ШшЩщЬьЪъЫыЭэЮюЯя 1 2 3 4 5 6 7 8 9 0
Кафедра инженерной графики
Разраб. Пров. Т.контр. Н.контр. Утв.
Изм. Докум. Подп. Дата Лит. Масса Масштаб Лист Листов СибГТУ Гр.91-1
ИГ00 01.1 07 07 00 ГН
Точка. Прямая.
Пересечение прямой с плоскостью
Метрические задачи
Сечение поверхности плоскостями
Пересечение поверхностей
ПРИЛОЖЕНИЕ в
(справочное)
Обозначения и условности
А, В, С … или 1, 2, 3… - точки в пространстве обозначаются прописными буквами латинского алфавита;
а, в, с… - линии (прямые и кривые) в пространстве – строчными буквами латинского алфавита;
h – горизонтальная, f – фронтальная, p – профильная прямые уровня;
Г – горизонтальная, Ф – фронтальная, - профильная плоскости уровня,
– проецирующие плоскости в пространстве обозначаются прописными буквами греческого алфавита;
, , - углы в пространстве – строчными буквами греческого алфавита;
П – плоскости в поле проекций – прописной греческой буквой с подстрочным индексом: П1 – горизонтальная, П2 – фронтальная, П3 – профильная плоскости проекций. Остальные плоскости проекций – П4, П5, П6… Пn.
А, А, а, а, , - последовательность геометрических элементов в пространстве – теми же буквами, но с надстрочными индексами. Проекции точек, линий, плоскостей, поверхностей, углов на комплексном чертеже обозначаются теми же буквами, что и в пространстве, но с добавлением подстрочного индекса 1, 2, 3, 4 …n, соответствующего плоскости проекций: на плоскости П1 – А1; П2 – А2; П3 – А3 … Пn – Аn.
А0, а0 – не проекционные элементы на комплексном чертеже – теми же буквами, но с надстрочным индексом ноль.
x, y, z, s – оси проекций в пространстве;
А , , а - новые положения геометрических элементов после вращения или параллельного перемещения – теми же буквами, но с одной чертой наверху после первого вращения, с двумя после второго.
Обозначение отношений между геометрическими элементами:
= или совпадают, результат действия, равны;
// - параллельны;
- перпендикулярны;
/ - скрещиваются;
- принадлежит, является элементом;
- включает, содержит;
U - объединение;
∩ - пересечени
Ирина Игоревна Астапкович
Татьяна Владимировна Борисова
Маргарита Николаевна Кузьмичёва
Ольга Степановна Мельникова
НАЧЕРТАТЕЛЬНАЯ ГЕОМЕТРИЯ
ИНЖЕНЕРНАЯ ГРАФИКА
Учебное пособие
|
|
|
 Скачать 1.75 Mb.
Скачать 1.75 Mb.
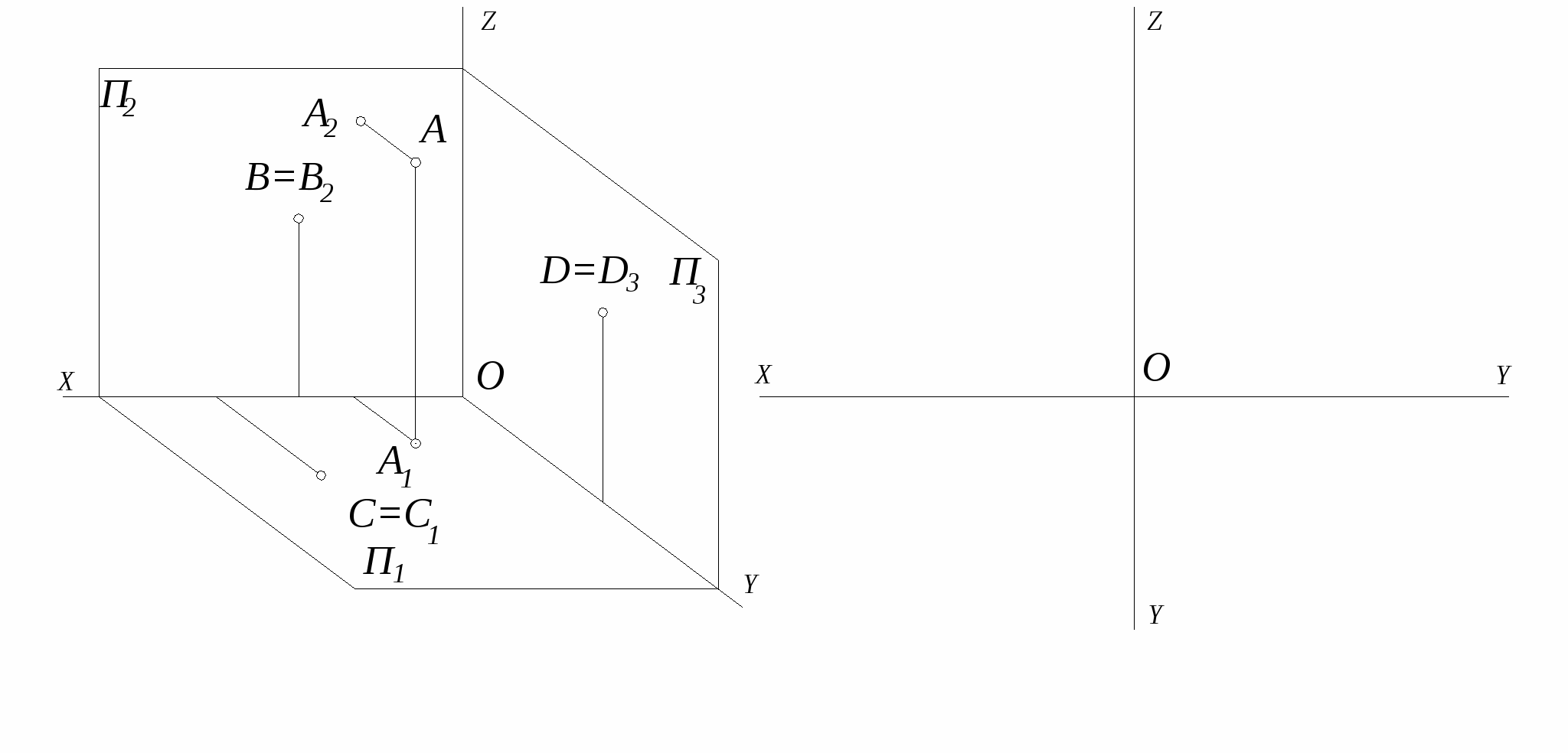
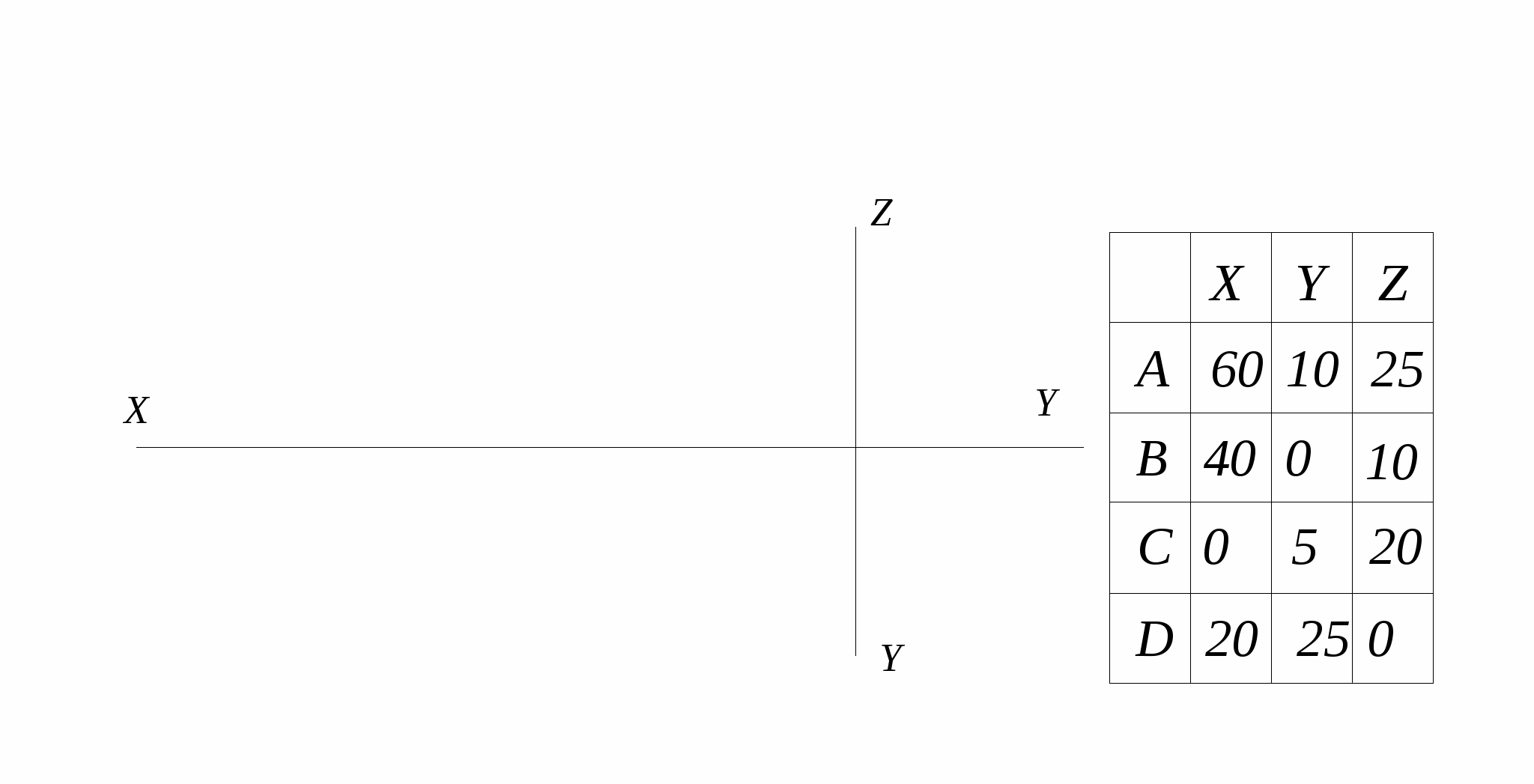 3. Относительно базовой точки А построить проекции точек:
3. Относительно базовой точки А построить проекции точек:
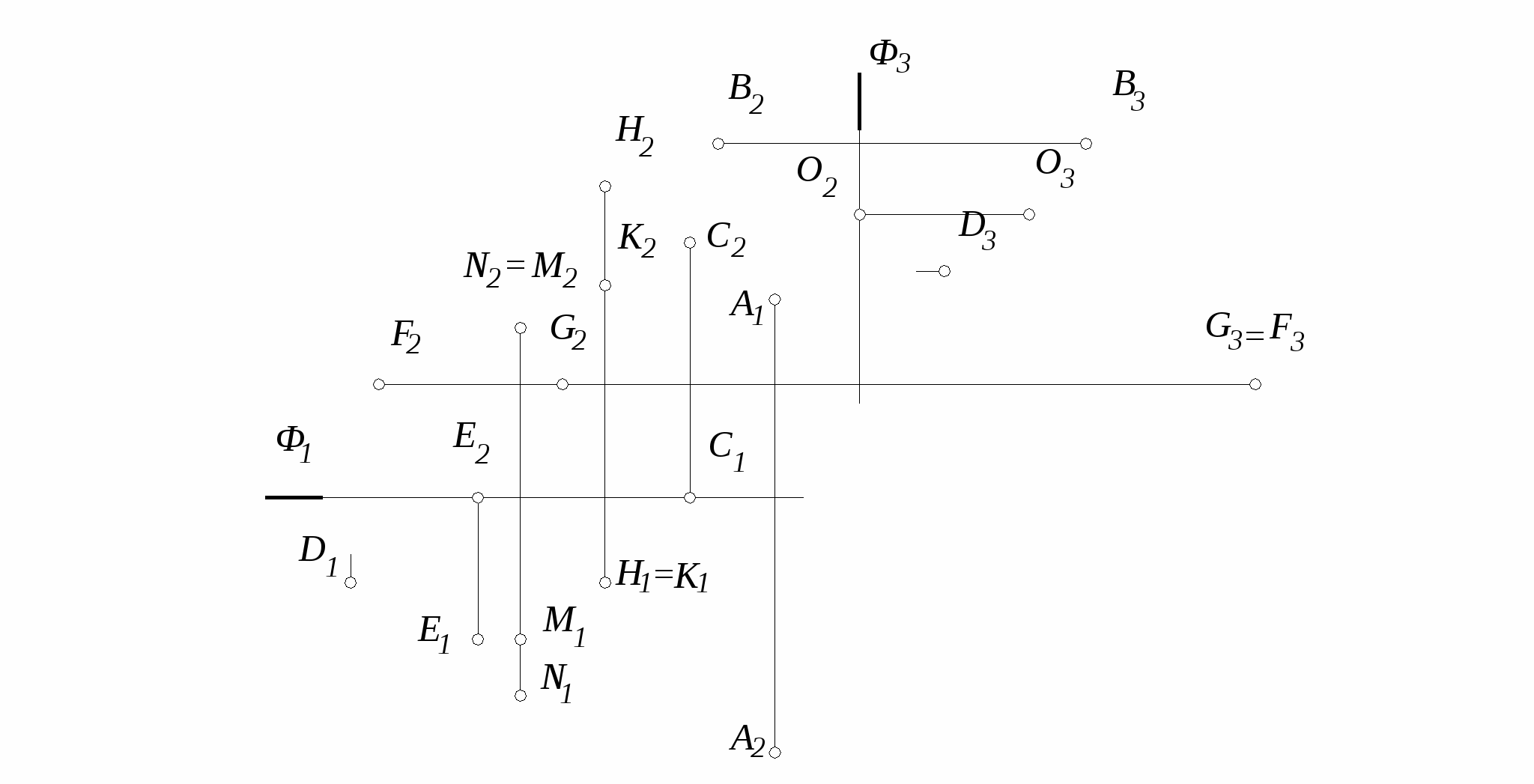

 В (А) – выше;
В (А) – выше; 
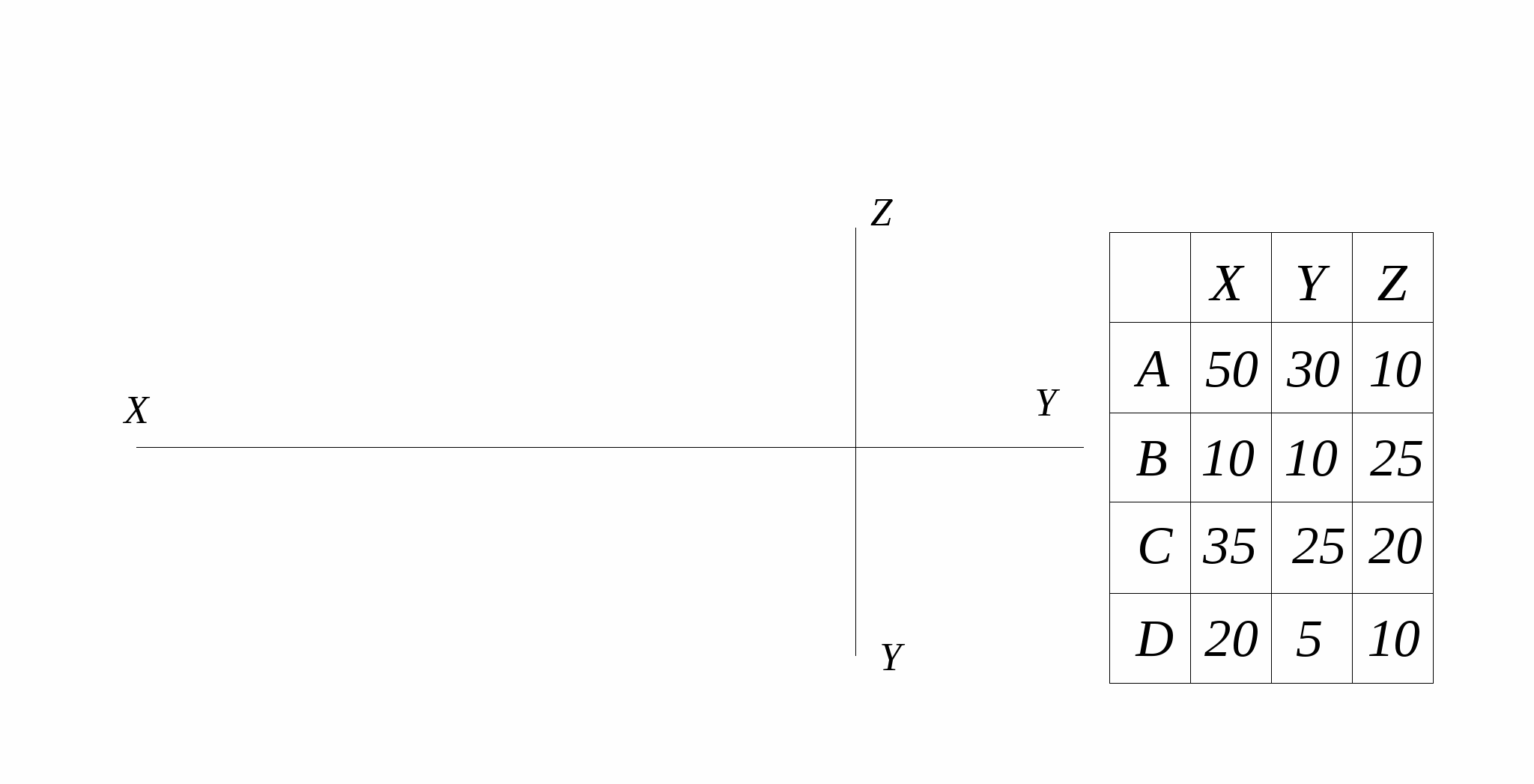











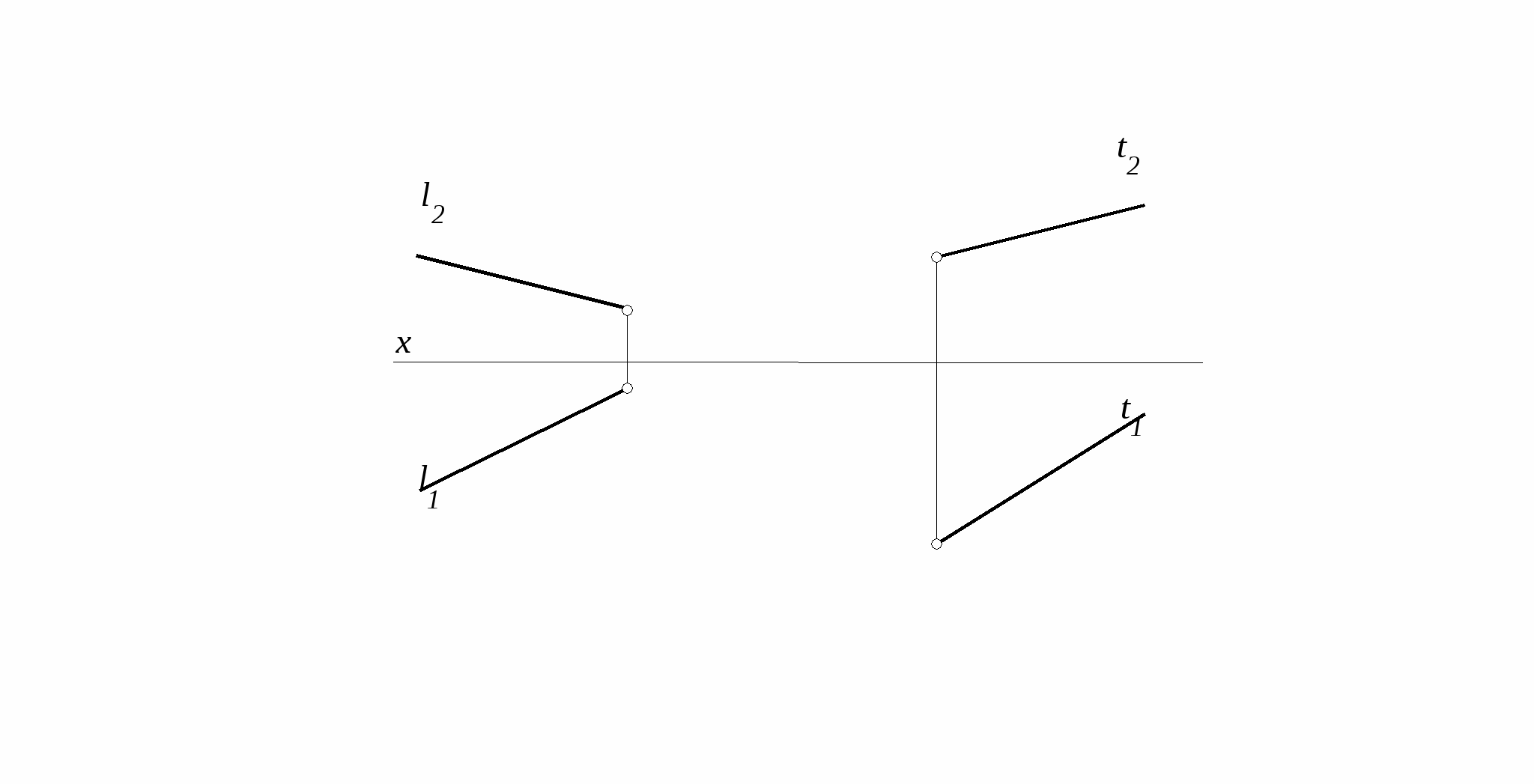












 _________________________________________________________________
_________________________________________________________________
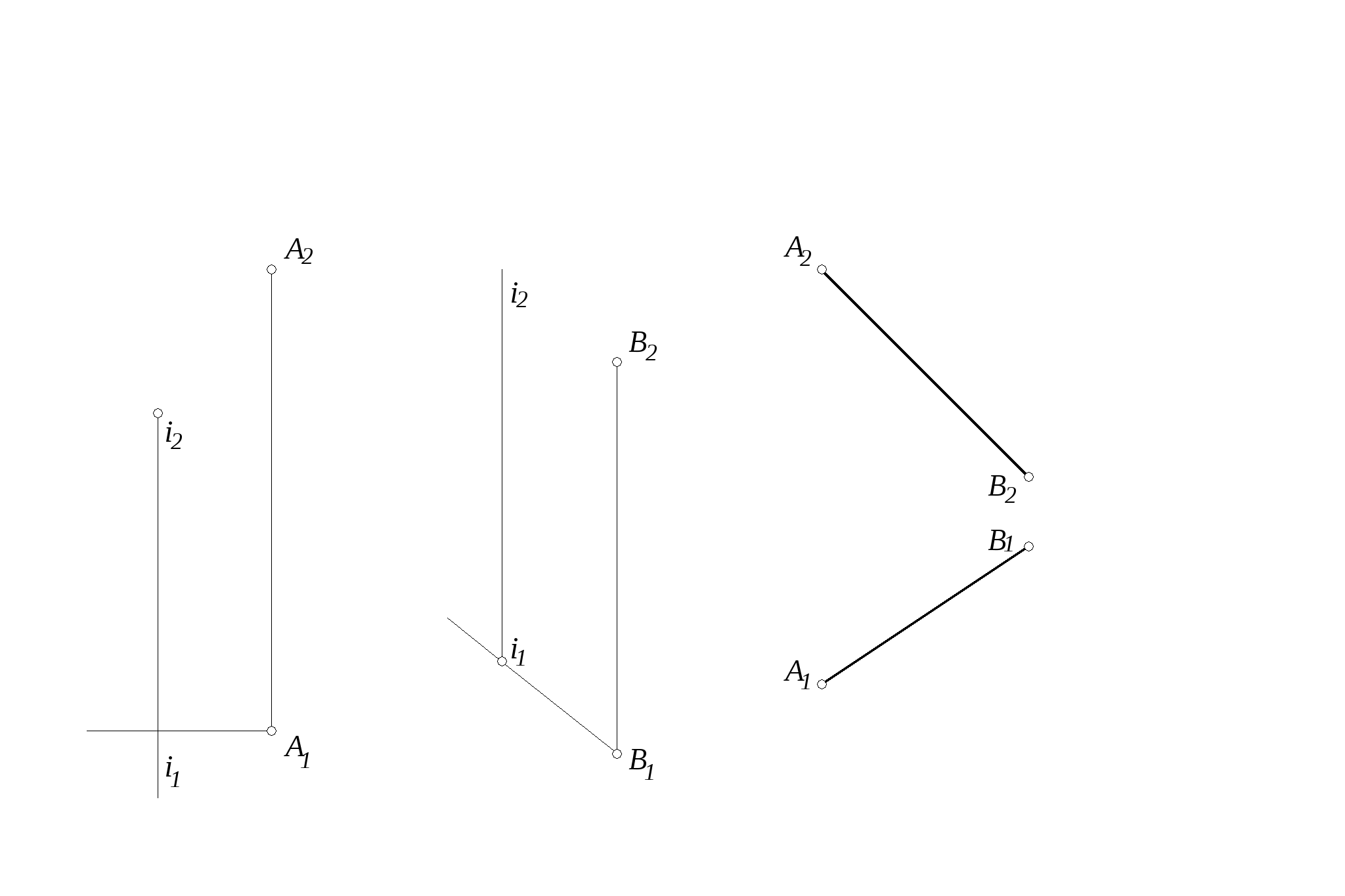


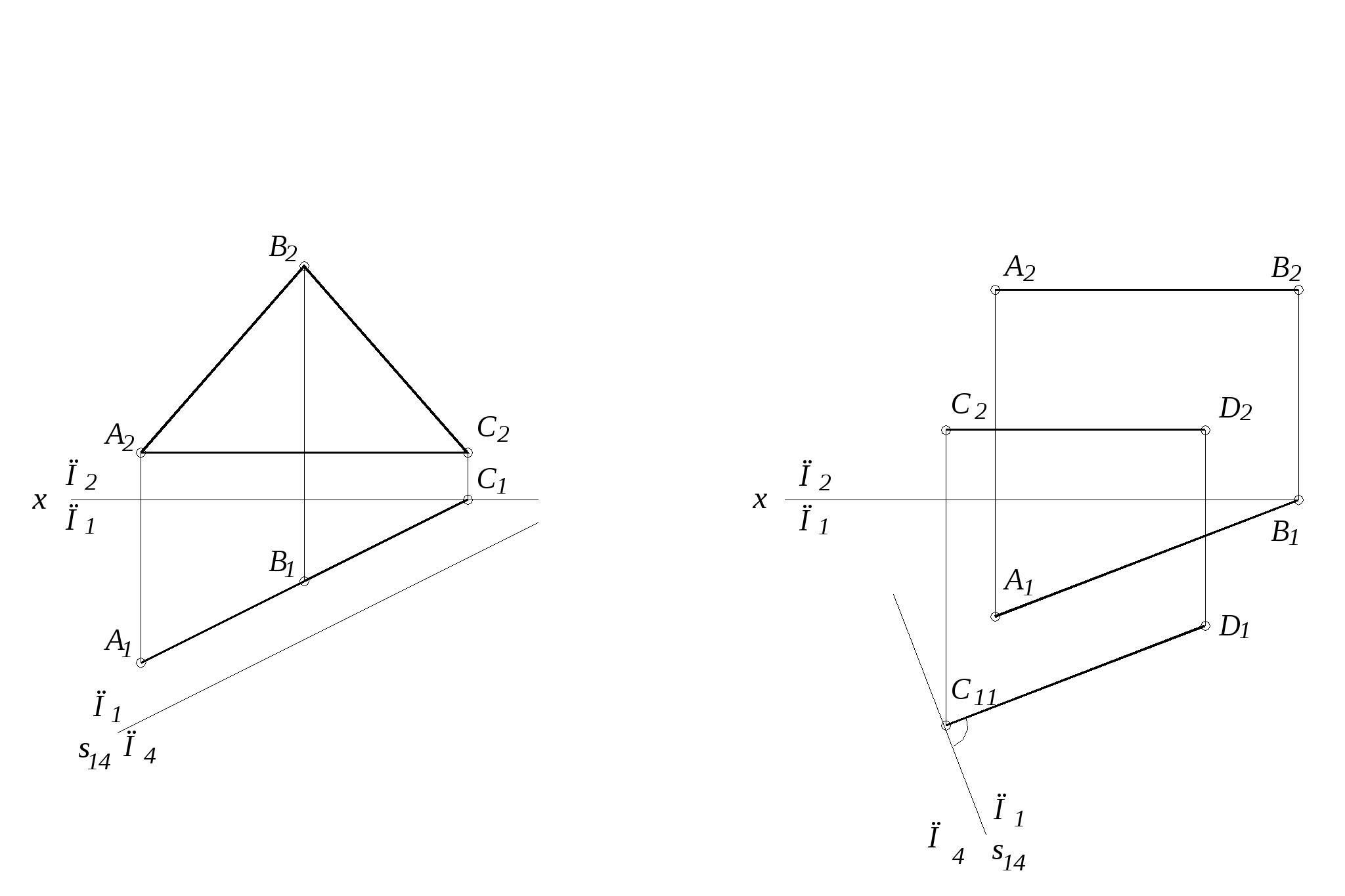






 45. Построить профильную проекцию призмы и найти недостающие проекции точек, принадлежащих граням этой призмы. Определить положение ребер и граней призмы относительно плоскостей проекций
45. Построить профильную проекцию призмы и найти недостающие проекции точек, принадлежащих граням этой призмы. Определить положение ребер и граней призмы относительно плоскостей проекций