высшая мат-ка. высшая математика 2. I и ii порядка Введение. Исследование
 Скачать 432.79 Kb. Скачать 432.79 Kb.
|
|
6. Дифференциальное уравнение первого порядка в полных дифференциалах. Определение. Пусть дифференциальное уравнение первого порядка представлено в виде M(x,y)dx+N(x,y)dx=0, Где M(x,y) и N(x,y) – функции двух переменных x и y. Тогда, если левая часть уравнения есть полный дифференциал некоторой функции U(x,y), т.е. dU(x,y)=M(x,y)dx+N(x,y)dy, то такое уравнение называется уравнением в полных дифференциалах. Уравнение в полных дифференциалах кратко можно представить в виде dU(x,y)=0, а поэтому общий интеграл (решение) такого уравнения имеет вид U(x,y)=0. Дифференциальное уравнение такого типа возникает, когда поведение системы подчинено условию сохранения некоторой величины U(энергии, массы, стоимости и т.д.). Отметим следующий признак, позволяющий определить является ли рассматриваемое уравнение уравнением в полных дифференциалах. Путьс dU(x,y)=M(x,y)dx+N(x,y)dy, тогда функции M(x,y) и N(x,y) должны быть для U(x,y) частными производными первого порядка, соответственно, по переменным x и y, т.е. 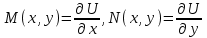 . .Предполагая функции M(x,y) и N(x,y) непрерывными и имеющими непрерывные частные производные, соответственно, по y и x, т.е. выполнение соотношений 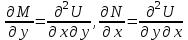 , ,из тождества 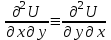 получаем, что для M(x,y) и N(x,y) должно выполняться условие 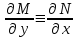 . .Полученное условие является не только необходимым, но и достаточным для того, чтобы уравнение M(x,y)dx+N(x,y)dy=0 Было уравнением в полных дифференциалах. Нахождение общего решения уравнения в полных дифференциалах проводится в два этапа. На первом этапе функция U(x,y) рассматривается как функция только аргумента x, переменная y получает как бы фиксированное значение 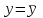 . Тогда соотношению . Тогда соотношению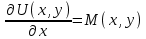 ставится в соответствие дифференциальное уравнение 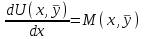 . .Пусть его общее решение представляется в виде 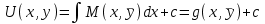 . .Но так как решение уравнения зависит от y, то в общем решении постоянная c является функцией y, т.е. c=h(y). Следовательно, общее решение предыдущего дифференциального уравнения, снимая с y условие закрепления его значения, имеет вид U(x,y)=g(x,y)+h(y). На втором этапе находится вид функции h(y). Для этого обратимся к соотношению 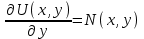 , ,в котором уже закрепляется как бы значение переменной x. Используя данное соотношение и вид функции U(x,y), получаем дифференциальное уравнение, связывающее переменные h и y: 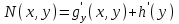 или или 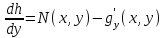 . .Интегрируя это уравнение, находим его общее решение 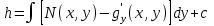 . .Из 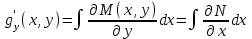 , получаем окончательный вид функции U(x,y), а именно , получаем окончательный вид функции U(x,y), а именно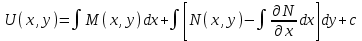 или или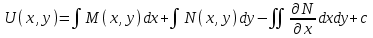 . .В последнем двойном интеграле вместо 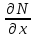 можно взять функцию можно взять функцию 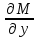 (т.к. (т.к. 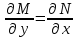 ). Тогда функция U(x,y) получает вид ). Тогда функция U(x,y) получает вид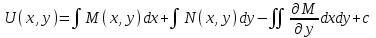 . .Так как общее решение исходного дифференциального уравнения записывается в виде U(x,y)=c=const, то, заменяя две постоянных на одну, получаем следующий вид общего решения уравнения 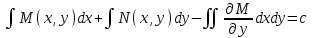 или или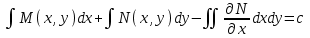 . .Пример 1. Дано дифференциальное уравнение (6x2y2+6xy-1)dx+(4x3y+3x2y+2y)dy=0. В нем M(x,y)=6x2y2+6xy-1, N(x,y)=4x3y+3x2y+2y. Из 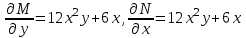 и тождества и тождества 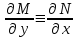 , ,Следует, что данное уравнение является уравнением в полных дифференциалах. Проведем его решение в два этапа. На первом решаем уравнение 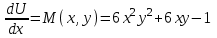 или dU=(6x2y2+6xy-1)dx, или dU=(6x2y2+6xy-1)dx,в котором переменная y считается закрепленной. Интегрируя это уравнение, получаем U(x,y)=2x3y2+3x2y-x+h(y). На втором этапе определяем вид функции h(y), используя для этого соотношение 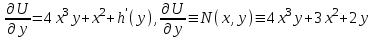 и дифференциальное уравнение для h и y 4x3y+3x2+h/(y)=4x3y+3x2+2y или 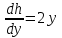 . .Интегрируя последнее, получаем h=y2+c. Общий интеграл исходного уравнения тогда можно записать в виде 2x3y2+3x2y-x+y2=c. Пример 2. Найти решение уравнения 2xsinydx+(3y2+x2cosy)dy=0. Проверяем, является ли оно уравнением в полных дифференциалах? Для этого из M(x,y)=2xsiny, N(x,y)=3y2+x2cosy Находим 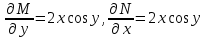 . .Так как, очевидно, выполняется условие 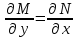 , ,то уравнение есть уравнение в полных дифференциалах. Сначала решаем уравнение 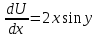 или dU=2xsinydx, или dU=2xsinydx,считая y постоянной. Интегрирование уравнения дает U(x,y)=x2siny+h(y). Затем находим функцию h(y), используя соотношения 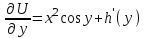 , с одной стороны, и , с одной стороны, и 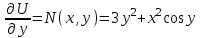 , с другой стороны. Соотношения приводят к дифференциальному уравнению , с другой стороны. Соотношения приводят к дифференциальному уравнению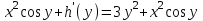 или или 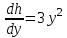 . .Интегрируя последнее уравнение, получаем h=y3+c. Тогда общий интеграл исходного дифференциального уравнения записывается в виде X2siny+y3+c=0. Далее рассмотрим понятие интегрирующего множителя. Ранее отмечалось, что уравнение в полных дифференциалах возникает, когда поведение системы сохраняет некоторую величину U, т.е. удовлетворяет соотношению U(x,y)=c. Дифференциальным аналогом его является уравнение dU(x,y)=0 или M(x,y)dx+N(x,y)dy=0, Где 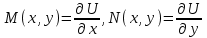 . .Предположим теперь, что частные производные функции U(x,y) представимы в виде 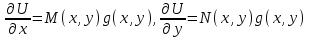 . .Тогда соотношению U(x,y)=e будет соответствовать уравнение в полных дифференциалах вида M(x,y)g(x,y)dx+N(x,y)g(x,y)dy=0. Если теперь данное уравнение разделить на общий множитель слагаемых g(x,y), то получим уравнение M(x,y)dx+N(x,y)dy=0. Решение последнего уравнения эквивалентно решению предыдущего, из которого оно получено, однако оно может уже не являться уравнением в полных дифференциалах, также для него возможно будет 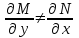 . .В то же время после умножения его на множитель g(x,y), оно становится уравнением в полных дифференциалах. Определение. Функция g(x,y) называется интегрирующим множителем дифференциального уравнения M(x,y)dx+N(x,y)dy=0, Если после умножения его на эту функцию оно становится уравнением в полных дифференциалах. Данный способ решения дифференциального уравнения называется методом интегрирующего множителя. Найдем условие, которому должен подчиняться интегрирующий множитель g(x,y). Из предложения, что уравнение M(x,y)g(x,y)dx+N(x,y)g(x,y)dy=0 Становится уравнением в полных дифференциалах следует выполнение условия 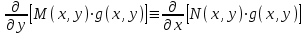 . .Разверернув левую и правую части этого тождества 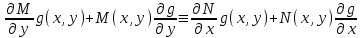 , ,заключаем, что функция g(x,y) должна являться решением уравнения 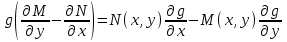 . .В общем случае решение данного уравнения вызывает затруднения. Отметим два случая, когда его решение становится проще. Случай первый. Пусть 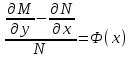 . .Тогда интегрирующий множитель можно искать в виде функции зависящей только от x. Действительно, пусть g=g(x). Тогда в виду 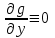 ; получаем, что искомая функция g(x) является решением дифференциального уравнения ; получаем, что искомая функция g(x) является решением дифференциального уравнения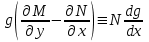 или или 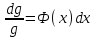 , ,интегрируя которое, находим 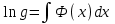 , т.е. , т.е. 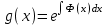 . .Второй слуяай относится к аналогичной ситуации, когда 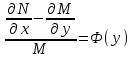 . .Тогда интегрирующий множитель ищется в виде функции только от y, т.е. g=g(y). Аналогично предыдущему, не трудно видеть, что функция g(y) является решением уравнения 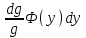 и представляется в виде 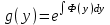 . .Пример 3. Дано уравнение (y2-3xy-2x2)dx+(xy-x2)dy=0. Из M(x,y)=y2-3xy-2x2, N(x,y)=xy-x2, 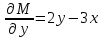 , , 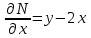 следует следует 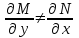 , т.е. уравнение не является в полных дифференциалах. , т.е. уравнение не является в полных дифференциалах.Однако из соотношения  вытекает, что можно найти такой интегрирующий множитель g=g(x), после умножения на который исходное уравнение становится уравнением в полных дифференциалах. Указанный множитель находим из уравнения 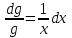 , ,интегрируя которое получаем 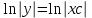 , или g=xc. Так как в качестве множителя достаточно взять одну из функций, то положим c=1 и, тогда, g=x. , или g=xc. Так как в качестве множителя достаточно взять одну из функций, то положим c=1 и, тогда, g=x.Умножая исходное уравнение на множитель g=x, получаем (xy2-3x2y-2x3)dx+(x2y-x3)dy=0, являющееся уже уравнением в полных дифференциалах. Интегрируя его, находим 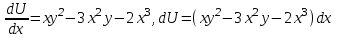 , ,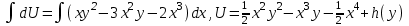 , ,затем из U/y=x2y-x3+h/(x) и U/y=N(x,y)=x2y-x3 получаем x2y-x3+h/=x2y-x3, т.е. 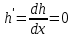 и, и,следовательно, h=c=const. Таким образом, общее решение имеет вид 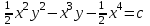 . .Пример 4. Требуется решить уравнение (2xy2-y)dx+(y2+x+y)dy=0. Из M(x,y)=2xy2-y, N(x,y)=y2+x+y, 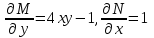 следует следует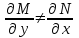 . .Однако из соотношения 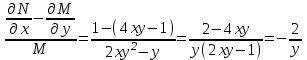 , ,вытекает, что для исходного дифференциального уравнения существует интегрирующий множитель g=g(y), с помощью которого уравнение становится уравнением в полных дифференциалах. Интегрирующий множитель находится из уравнения 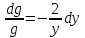 . .Интегрируя его, получаем 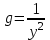 . .Умножая исходное уравнение на множитель 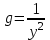 , приходим к уравнению , приходим к уравнению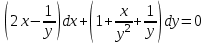 . .Это уравнение является уже уравнением в полных дифференциалах. Решаем его 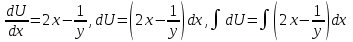 , ,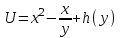 , ,затем из 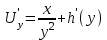 и и 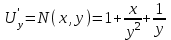 , ,получаем 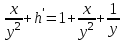 или или 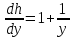 . .Интегрируя последнее уравнение, имеем 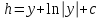 . .Таким образом, общий интеграл исходного уравнения имеет вид 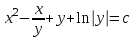 . .7. Дифференциальные уравнения второго порядка. Обыкновенное дифференциальное уравнение второго порядка имеет следующий общий вид F(x,y,y/,y//)=0 или 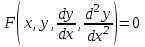 . .Наше знакомство с дифференциальными уравнениями второго порядка будет ограничено рассмотрением линейного дифференциального уравнения второго порядка с постоянными коэффициентами. Определение. Линейным дифференциальным уравнением второго порядка с постоянными коэффициентами называется уравнение вида y//+py/+qy=h(x), где p и q – числа, h(x) – некоторая функция от x. Если в этом уравнении 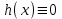 , то оно называется однородным линейным дифференциальным уравнением второго порядка. , то оно называется однородным линейным дифференциальным уравнением второго порядка.Рассмотрим решение однородного уравнения 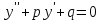 . .Этому явлению может быть поставлено в соответствие квадратное уравнение вида 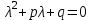 , ,Называемое характеристическим. Его корни 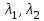 , как известно, определяются формулами , как известно, определяются формулами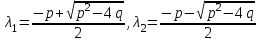 . .Возможны следующие три случая для вида корней 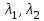 этого уравнения: 1) корни уравнения – действительные и различные; 2) корни – действительные и равные; 3) корни уравнения – комплексно-сопряженные. Для каждого из этих случаев однородное дифференциальное уравнение имеет свой вид общего интеграла. этого уравнения: 1) корни уравнения – действительные и различные; 2) корни – действительные и равные; 3) корни уравнения – комплексно-сопряженные. Для каждого из этих случаев однородное дифференциальное уравнение имеет свой вид общего интеграла.Случай 1. Дискриминант характеристического уравнения положителен, т.е. p2-4q>0. Тогда оба корня 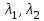 действительные и различные. В этом случае общее решение однородного уравнения имеет вид действительные и различные. В этом случае общее решение однородного уравнения имеет вид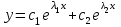 , ,где c1, c2 – произвольные постоянные. Действительно, если 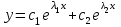 , то , то 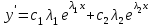 , , 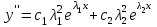 . Подставляя выражения для y,y/ и y// в уравнение получим . Подставляя выражения для y,y/ и y// в уравнение получим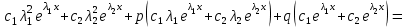 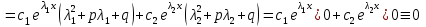 . .Случай 2. Дискриминант характеристического квадратного уравнения равен нулю, т.е p2-4q=0. Тогда оба корня 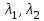 действительные и равные, т.е. действительные и равные, т.е. 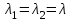 . .В этом случае общее решение однородного уравнения имеет вид 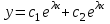 . .Случай 3. Дискриминант характеристического квадратного уравнения отрицателен, т.е. p2-4q<0. Тогда говорят, что квадратное уравнение не имеет действительных корней (или что оба корня являются комплексно-сопряженными). В этом случае, обозначая 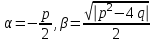 , общее решение однородного уравнения дается в виде , общее решение однородного уравнения дается в виде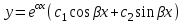 . .Рассмотрим теперь решение неоднородного уравнения y//+py/+g(y)\h(x), где h(x) – некоторая функция от x. Пусть в этом уравнении q=0, тогда, используя подстановку y/=z, y//=z/, приходим к решению линейного дифференциального уравнения первого порядка z/+pz=h(x). |
