Задание № 2 - кинематика точки. И инженерной графики
 Скачать 77.42 Kb. Скачать 77.42 Kb.
|
|
российский государственный геологоразведочный университет имени серго орджоникидзе (МГРИ) кафедра механики И ИНЖЕНЕРНОЙ ГРАФИКИ Расчетная работа по теоретической механике № 2 Кинематическое исследование движения точки по заданным уравнениям движения в декартовых координатах Вариант № 14 Выполнил: студент группы студенческий билет № ___________________ _____________ ___________________ (подпись) (ФИО) Проверил: доцент каф. Механики и инженерной графики Москва, 2022 Точка М движется в плоскости OXY (рис.). Траектория точки на рисунках показана условно. Закон движения точки задан уравнениями x = f1(t); y = f2(t), где x и y выражены в см, t - в с. Найти уравнение траектории точки, определить скорости и ускорения точки, а также ее касательное и нормальные ускорения, радиус кривизны в соответствующих точках траектории, для момента времени t = 1с. Указания. Задание относится к кинематике точки и решается с помощью формул, по которым определяются скорость и ускорение точки в декартовых координатах, а также формул для определения тангенциального и нормального ускорения точки. В данном задании все кинематические характеристики движения определяются для моментов времени t = 0 с и t = 1 с. При решении некоторых вариантов следует учесть известные тригонометрические зависимости: cos2 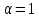 - 2·sin2 - 2·sin2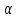 = 2·cos2 = 2·cos2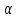 – 1; – 1;sin 2·  2·sin 2·sin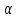 ·cos ·cos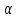 . .
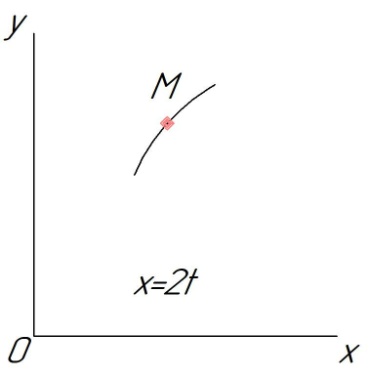 Рис. 2. 4 Решение: 1. Определим уравнение траектории, по которой движется точка М. Для этого представим уравнение в виде x = 2·t => t = x/2 ; y = 8·sin( 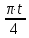 ) . ) .Тогда y = 8·sin( 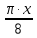 ) . ) .Это уравнение синусоиды: у , см 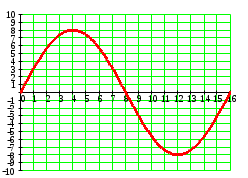 х , см х , смрис. 1, а Из уравнений для x и y следует, что х ≥ 0 ; -8 ≤ у ≤ 8 . Таким образом, траекторией точки М является колебательный процесс с амплитудой А = 8 см . График траектории точки M показан на рис. 1, а . 2. Определяем начальное положение М0 точки и направление ее движения. При t = 0 x0 = 0; y0 = 0 . В начальный момент времени точка находится в начале координат и движется слева направо . При t = 1 с x = 2 см ; y = 4·√2 см . 3. Определяем скорость точки М vx = 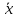 = dx/dt = 2 ; = dx/dt = 2 ;vy = 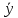 = dy/dt = 2·π·cos ( = dy/dt = 2·π·cos (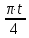 ) . ) . Модуль скорости:  = = 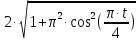 . .Направление вектора скорости: 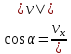 = = 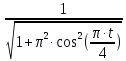 ; ;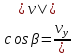 = = 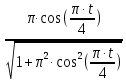 , ,где α и β – углы между направлением вектора скорости v и положительным направлением осей координат OX и OY соответственно. При t = 1 с получаем: vx = 2 см/с ; vy = 0 см/с ; α = 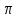 ; β = ; β = 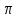 /2 . /2 .4. Определяем ускорение точки М ax = 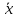 = d2x/dt2 = -2 = d2x/dt2 = -2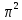 sin sin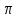 t ; t ;ay = 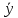 = d2y/dt2 = - 4 = d2y/dt2 = - 4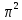 cos2 cos2 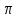 t . t .Модуль полного ускорения 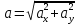 = =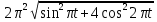 Направление вектора ускорения: 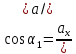 = = 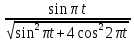  = = 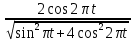 где α1 и β1 – углы между направлением вектора полного ускорения a и положительными направлениями осей OX и OY. Касательное (тангенциальное) ускорение найдем, дифференцируя по времени уравнение скорости 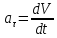 , но учитывая, что , но учитывая, что2v 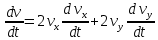 или va = vXaX + vYaY , или va = vXaX + vYaY ,Получаем 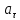 = =  = == 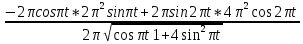 = ==  = == 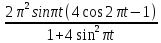 Нормальное ускорение определяется из равенства an = 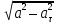 = = 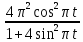 При t = 1с ax = 0; ay = 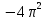 ; a = ; a = 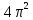 ; a = 0; an = ; a = 0; an =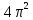 ; α1 = - ; α1 = -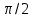 ; β1 = ; β1 = 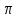 5. Находим радиус кривизны траектории в функции времени: 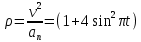 3/2 3/26. Проверяем правильность вычисления радиуса кривизны траектории по формуле: 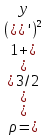 Вычисляем производные: y‘ = dy/dx = -x; y’’ = d2y/dx2 = -1 Тогда 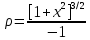 = (1+4sin2 = (1+4sin2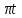 )3/2 )3/2При t = 1с 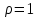 см. см.На траектории (рис. 1, б) показывают положение точки М при t = 1 с и направления векторов v; an ; 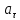 ; a. ; a. а) 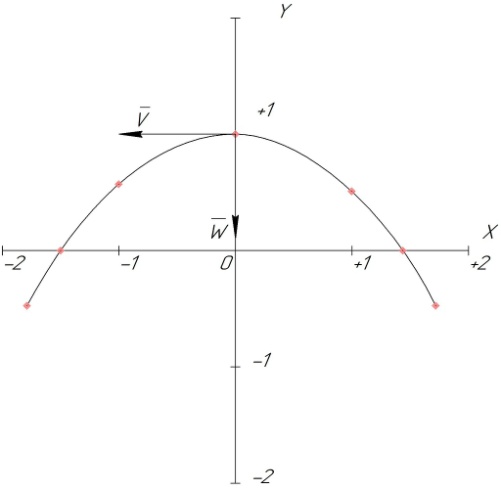 б) Рис. 1 (а, б) |
