Курсовая работа мтуси отс. кр. И массовых коммуникаций российской федерации
 Скачать 0.83 Mb. Скачать 0.83 Mb.
|
|
Сигнал ДЧМ представляется в виде: 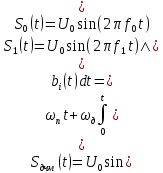 Где ωп – частота переносчика, ωд – девиация частоты. 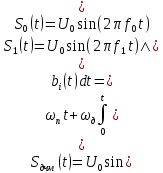 Разложение сигнала в ряд по гармоническим составляющим: 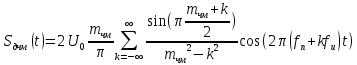 Где 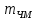 – индекс частотной модуляции – индекс частотной модуляции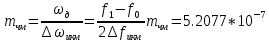 Bычислим ширину спектра ДЧМ: 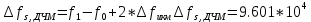 При неизвестной амплитуде 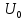 вычисляют нормированный спектр: вычисляют нормированный спектр: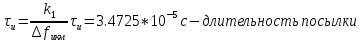 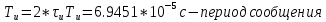 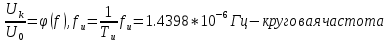 построить в масштабе график нормированного спектра сигнала дискретной модуляции и отметить на нем найденную ширину спектра. 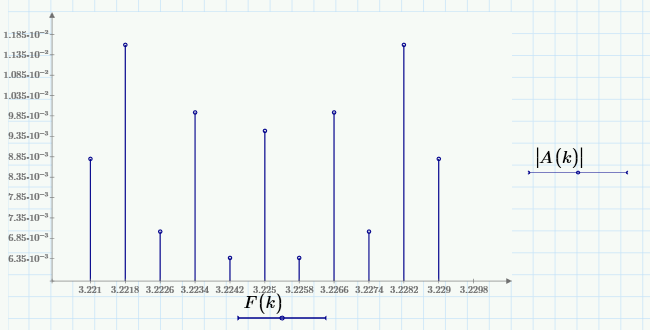 Рисунок 7 - График нормированного спектра сигнала ДЧМ Значения нормированного спектра  Рассматривая НКС как аддитивный гауссовский канал с ограниченной полосой частот, равной ширине спектра сигнала дискретной модуляции, и заданными спектральной плотностью мощности помехи и отношения сигнал-шум: рассчитать приходящиеся в среднем на один двоичный символ мощность и амплитуду модулированного, дисперсию (мощность) аддитивной помехи в полосе частот сигнала, дисперсию (мощность) аддитивной помехи в полосе частот сигнала, пропускную способность НКС; Мощность гауссовского белого шума: 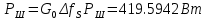 Мощность сигнала дискретной модуляции: 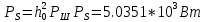 Мощность и амплитуда модулированного сигнала, приходящиеся в среднем на один двоичный символ: 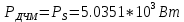 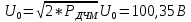 Пропускная способность НКС: 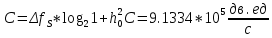 построить в масштабе четыре графика ФПВ мгновенных значений и огибающих УГП, и суммы гармонического сигнала с УГП. 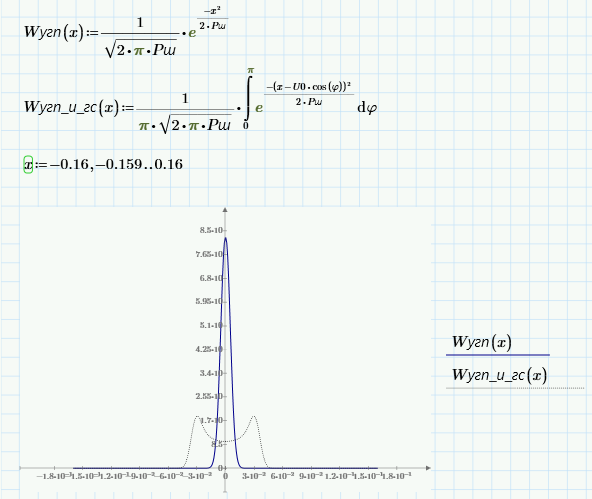 Рисунок 8- График функции плотности вероятности УГП и УГП+ГС 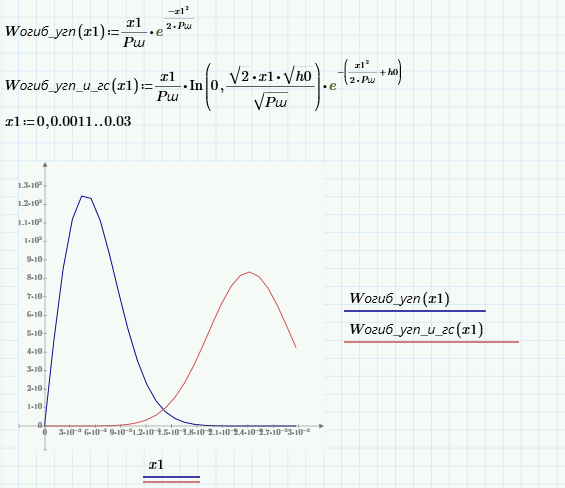 Рисунок 9 – График огибающих УГП и УГП+ГС С учетом заданного вида приема (детектирования) сигнала дискретной модуляции: рассчитать среднюю вероятность ошибки в двоичном ДКС, скорость передачи информации по двоичному симметричному ДКС. показатель эффективности передачи сигнала дискретной модуляции по НКС; За количественную меру помехоустойчивости в системах электросвязи принимают среднюю на бит вероятность ошибки: 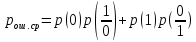 При равенствах априорных вероятностей р(0) = р(1) = 0.5, а также условных вероятностей р(1/0) = р(0/1) = рош (условие симметричности двоичного ДКС), средняя на бит вероятность ошибки равна рош.ср = рош 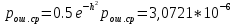 Скорость передачи информации по двоичному симметричному ДКС: 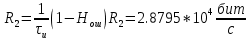 Показатель эффективности системы передачи: 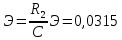 изобразить схему приемника сигналов дискретной модуляции и коротко описать принцип его работы, пояснить случаи. когда он выносит ошибочные решения. Приемник сигналов ДЧМ     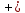 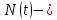 помеха (шум) в НКС помеха (шум) в НКС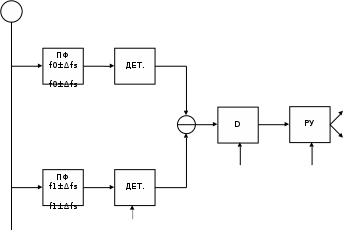   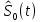  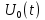 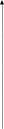   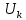 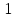  ВУ      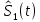 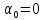 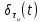  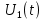 Детектор – это линейная система с переменными параметрами Схема детектора состоит из перемножителя и ФНЧ, прошедшего полосовой фильтр с эффективной полосой пропускания равной 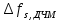 К детектору подводятся опорный сигнал 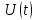 и далее перемножается с принятым, потом эти сигналы поступают на вычитающее устройство, далее сигнал поступает на дискретизатор к которому подводится последовательность дискретизирующих импульсов и далее перемножается с принятым, потом эти сигналы поступают на вычитающее устройство, далее сигнал поступает на дискретизатор к которому подводится последовательность дискретизирующих импульсов 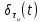 с периодом с периодом 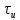 . .В РУ отсчеты 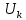 сравниваются с пороговым напряжением сравниваются с пороговым напряжением 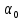 и если и если 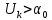 , то передана 1, или если , то передана 1, или если 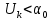 , то передан 0. Из-за помех в канале связи амплитуда сигнала изменяется и РУ может ошибаться: при передаче 0 принимать 1 или же при передаче 1 принимать 0. , то передан 0. Из-за помех в канале связи амплитуда сигнала изменяется и РУ может ошибаться: при передаче 0 принимать 1 или же при передаче 1 принимать 0.Рассматривая отклик декодера ПРУ как случайный дискретный сигнал на выходе 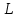 -ичного ДКС: -ичного ДКС:рассчитать распределение вероятностей дискретного сигнала на выходе декодера, скорость передачи информации по 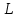 -ичного ДКС, относительные потери в скорости передачи информации по -ичного ДКС, относительные потери в скорости передачи информации по 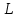 -ичного ДКС; -ичного ДКС;Распределение вероятностей дискретного сигнала на выходе детектора: 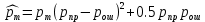
Энтропия ошибочных решений: 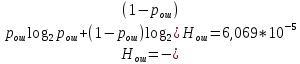 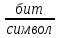 Энтропия восстановленного L-ичного сигнала: 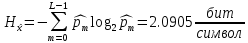 Скорость передачи информации по L-ичному ДКС: 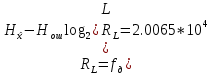 Относительные потери в скорости: 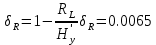 построить в масштабе график закона распределения вероятностей отклика декодера и сравнить его с законом распределения вероятностей отклика квантователя. 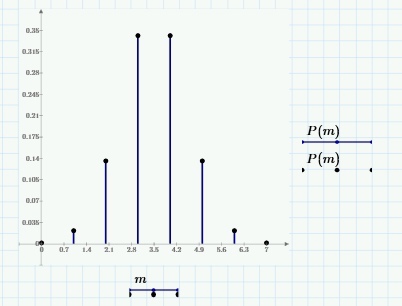 Рисунок 10 - Закон распределения вероятностей отклика декодера Полагая ФНЧ на выходе ЦАП приемника идеальным с полосой пропускания, равной начальной энергетической ширине спектра исходного сообщения: рассчитать дисперсию случайных импульсов шума передачи на выходе интерполятора ЦАП, СКПП, ССКП и ОСКП; Рассчитать дисперсию случайных импульсов шума передачи на выходе интерполятора ЦАП, среднюю квадратическую погрешность шума передачи (СКПП), суммарную начальную СКП восстановления непрерывного сообщения (ССКП), относительную СКП (ОСКП). 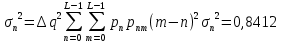 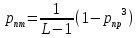 СКПП: 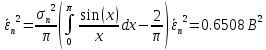 ССКП: 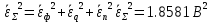 ОСКП: 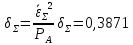 |