Гармонические колебания (1). I. механические колебания колебательным движением называют всякий процесс

• Название: I. механические колебания колебательным движением называют всякий процесс
• Дата: 28.12.2020
• Размер: 397 Kb.
• Имя файла: Гармонические колебания (1).doc
• Тип: Документы; #165022

I. МЕХАНИЧЕСКИЕ КОЛЕБАНИЯ
Колебательным движением называют всякий процесс,

характеризуемый той или иной степенью повторяемости: колебания ветвей деревьев, струн музыкальных инструментов, шатунов в поршневых двигателях, напряжения и тока в колебательном контуре, вибрации мостовых конструкций, фундаментов и т.д.

Для возникновения колебаний необходимо выполнение следующих трех

условий:

1. 
   система должна иметь положение равновесия;
   
2. 
   при отклонении от равновесия появляется возвращающая сила;
   
3. 
   инерционность системы не позволяет ей сразу остановиться и поэтому она “проскакивает” положение равновесия.
   

1. 
   Гармонические колебания
   

Наиболее простым видом колебаний являются гармонические колебания,

совершаемые по закону синуса или косинуса:

,	(1.1)
,	(1.2)

где x – смещение колеблющейся точки от положения равновесия;

А – амплитуда колебаний, т.е. модуль максимального смещения точки;

t + ₀ – фаза колебания; ₀ – начальная фаза, т.е. значение фазы в момент времени t = 0;  - круговая (циклическая) частота колебания. Заметим, что для перехода от выражения (1.1) к выражению (1.2) достаточно изменить на /2 начальную фазу колебания.

Широко используются связанные с круговой частотой характеристики колебаний – период и частота. Периодом Т называют время совершения одного полного колебания, при этом

.

(1.3)

Частота  - число колебаний, совершаемых в единицу времени, очевидно,

(1.4)

Единицы измерения рассмотренных величин в СИ: смещения и амплитуды – 1 м; фазы – 1 рад (радиан); круговой частоты – 1 рад/с; периода – 1 с; частоты –

1 Гц (герц) = 1 с^-1. Широко применяются внесистемные единицы частоты: килогерц

(1 кГц = 10³ Гц) и мегагерц (1 МГц = 10⁶ Гц). Фазу в ряде случаев измеряют в угловых градусах (180⁰ =  рад  3,14 рад).

В дальнейших рассуждениях и при решении задач будем исходить из формулы (1.1).

Скорость колеблющейся точки:

(1.5)

Ускорение:

(1.6)

Модули смещения, скорости и ускорения достигают максимальных значений, когда становятся равными  1 значения тригонометрических функций, входящих в соответствующие уравнения:

	(1.7)
	(1.8)

(1.9)

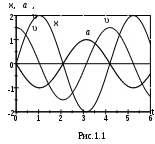x_m, _m, называются соответственно: амплитуда смещения, амплитуда скорости и амплитуда ускорения.

Как видно из выражений (1.5) и (1.6), величины скорости и ускорения при гармоническом колебании также изменяются по гармоническому закону, при этом скорость опережает смещение по фазе на /2, а величина ускорения совершает колебания в противофазе к смещению (опережает или отстает на ). Графики зависимости от времени t смещения x, скорости  и ускорения приведены на рис. 1.1.

Рассмотренные выше соотношения являются кинематическими. С точки зрения динамики гармоническими являются колебания, совершаемые под действием упругой или квазиупругой силы. Согласно закону Гука, величина упругой силы

(1.10)

где x – величина деформации,

k – коэффициент жесткости тела.
Под квазиупругой (как бы упругой) понимают неупругую по природе силу, величина которой пропорциональна смещению точки от положения равновесия, а направление – противоположно смещению, т.е. для квазиупругих сил равенство (1.10) такжесправедливо. Обычно эти силы называют возвращающими, т.к. они в любой момент всегда направлены к положению равновесия. Описываемый ниже пружинный маятник совершает колебания под действием упругой силы, а математический и физический – под действием квазиупругой. Следует отметить, что во всех трех случаях речь идет о свободных (собственных) колебаниях, которые совершаются системой, выведенной из положения равновесия и предоставленной затем с самой себе.

Важно заметить, что мы рассматриваем лишь малые колебания маятников, т.к. только при этом условии величина возвращающей силы пропорциональна смещению от положения равновесия.

Величина возвращающей силы определяется по второму закону Ньютона: . С учетом выражения (1.6)

.

(1.11)

Сравнение (1.10) и (1.11) приводит к выражению

.

(1.12)

Из (1.11) и (1.12) следует, что амплитуда силы

.

(1.13)

Пружинный маятник представляет собой груз (материальную точку), подвешенный на пружине. Период свободных колебаний пружинного маятника

(1.14)

где m – масса груза; k – коэффициент жесткости пружины.

Математический маятник – материальная точка, подвешенная на невесомой, нерастяжимой нити, совершает колебания с периодом

(1.15)

где – длина маятника; g  9,81 м/с² – ускорение свободного падения.

Физическим маятником называют твердое тело, совершающее под действием силы тяжести колебания вокруг горизонтальной оси, называемой осью качания. Период свободных колебаний физического маятника определяется по формуле

(1.16)

где J - момент инерции маятника относительно оси качания;

m – его масса; – длина маятника, под которой понимают расстояние от оси качания до центра масс (центра тяжести) маятника.

(1.17)

Момент инерции физического маятника относительно оси качания может быть определен по теореме Штейнера:

(1.18)

где J₀ – момент инерции тела относительно оси, проходящей через центр масс тела и параллельной оси качания; b – расстояние между этими осями; m – масса тела.

Напомним формулы, по которым определяются моменты инерции некоторых тел:

материальной точки массой m, движущейся по окружности радиуса R:

(1.19)

тонкого обруча (или тонкостенного полого цилиндра) массой m радиуса R относительно оси, совпадающей с его геометрической осью вращения:

(1.20)

сплошного однородного диска (цилиндра) массой m относительно оси, совпадающей с его геометрической осью вращения:

(1.21)

сплошного однородного шара радиуса R относительно оси, проходящей через его геометрический центр:

(1.22)

тонкого стержня длиной относительно оси, перпендикулярной ему и проходящей через его середину:

(1.23)

Потенциальная энергия материальной точки, совершающей свободные гармонические колебания:

(1.24)

(1.24)

Кинетическая энергия

(1.25)

Если система, совершающая колебания, замкнута и консервативна, то ее полная механическая энергия

(1.26)

(см. закон сохранения механической энергии).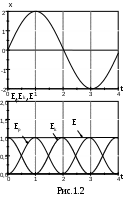


Очевидно, при этом не будет изменяться и амплитуда А колебания, т.е. колебания будут незатухающими.

На рис. 1.2 изображен график гармонического колебания (верхний чертеж) и графики зависимости от времени потенциальной, кинетической и полной механической энергии колеблющейся системы.

Анализ формул (1.24) и (1.25) и графика (рис. 1.2) приводит к выводу:

когда

(1.27)

когда

(1.28)

ПРИМЕРЫ РЕШЕНИЯ ЗАДАЧ
Задача 1.1. Точка совершает гармоническое колебание с частотой

2 Гц. В момент времени t = 0 скорость точки достигает максимального значения


Дано:

 = 2 Гц;

_max = 60 см/с =

=0,60 м/с




x = f (t) - ?

_max = 60 см/с. Записать (с числовыми коэффициентами) закон движения x = f (t) точки.

Решение:

Для того, чтобы записать закон движения (см. формулу (1.1)) с числовыми коэффициентами, нужно определить

величины А,  и ₀.

Круговую частоту  определим из формулы (1.4):


Для определения амплитуды колебания воспользуемся формулой (1.5).

Максимального (по модулю) значения _max скорость достигает при

(см. формулу (1.8)), откуда



Определим теперь начальную фазу ₀ колебания. По условию задачи в момент времени t = 0 скорость . Из уравнения (1.5):



тогда



Запишем закон движения:



Д ано:

t = 2 c

x = f (t) - ?

x - ?  - ?

- ?
Задача 1.2. На рис.1.3 показан график зависимости ускорения 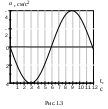точки от времени t при гармоническом колебании. Записать закон движения x = f (t) колеблющейся точки, определить смещение, скорость и ускорение точки в момент времени t = 2 c.

Р ешение:

Для записи закона движения точки нужно,

как и в задаче 1.1, определить величины

А, , и ₀. Как видно из графика рис.1.3,

период колебания Т = 12 с, следовательно,

круговая частота



Для определения амплитуды колебания проанализируем формулы (1.6) и (1.9):

, значит, откуда Величину определим из графика:



Тогда

Величину ₀, на первый взгляд, проще всего определить, рассмотрев колебание в момент времени t = 0, когда = 0. Однако у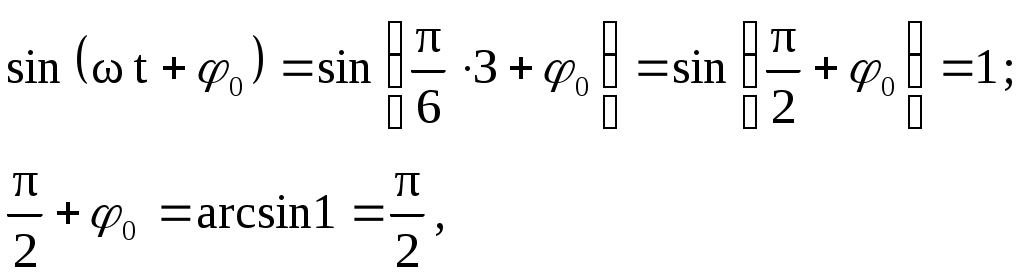скорение (так же, как и величины x и ) принимает равное нулю значение дважды за период, что может привести к ошибке в определении начальной фазы. Для исключения ошибки рассмотрим колебание в момент

t = 3 с, когда (с таким же успехом можно провести решение и для момента t = 9 c, когда ). Итак, для момента t = 3 c:



откуда



Запишем закон движения:


Определим величины x,  и для момента времени t=2 c:






Задача 1.3. К спиральной пружине подвешен грузик, в результате чего пружина растянулась на 4,6 см. Каков будет период колебаний грузика, если его немного оттянуть вниз и затем отпустить?


Дано:

x₀ = 4,6 см =

=4,610^-2 м;

g  9,81 м/с²




Т - ?
Решение:

Описанная в условии задачи система представляет собой пружинный маятник, период свободных колебаний которого определяется по формуле (1.14):

(1.29)

В данном случае силой, растягивающей пружину в состоянии покоя (до начала колебаний), является сила тяжести грузика P = mg, которая уравновешивается упругой силой, возникающей в пружине: .

Согласно закону Гука тогда в нашем случае



Подставив величину k в уравнение (1.29), получим:



(Для упрощения расчетов можно считать, что ²  g или ).
Задача 1.4. Однородный диск радиусом 20 см колеблется около горизонтальной оси, проходящей по образующей цилиндрической поверхности диска. Определить период свободных колебаний такого маятника.


Дано:

R = 20 см =

=0,20 м;

g  9,81 м/c²




Т - ?
Решение:

Диск (см. рис.1.4), описанный в условии задачи, представляет собой физический маятник, период колебаний которого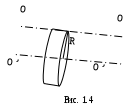


(1.30)

(см. формулу (1.16)).

Момент инерции J относительно оси качания ОО найдем, используя теорему Штейнера:



где - момент инерции диска относительно оси , проходящей через центр масс диска; b – расстояние между осями. В нашем случае b = R, тогда



Длина маятника в нашем случае также равна радиусу диска ( = R). Подставив значения J и в формулу (1.30), получим:


Задача 1.5. Колебания материальной точки массой 12 г совершаются согласно закону Определить амплитуды (т.е. максимальные значения) возвращающей силы и кинетической энергии точки.


Дано:

m = 12 г = 1,210^-2 кг

x = 0,06 sin 10t м



F_m - ? E_кm - ?

Решение:

Способ 1:

Величина возвращающей силы в любой момент времени .

Ускорение



Максимальная величина ускорения = 6 м/с², тогда

амплитуда силы

F_m = m = 1,210^-26 Н = 7,210^-2 Н = 72 мН

Амплитуда кинетической энергии , скорость колеблющейся точки



Очевидно, что _m = 0,6 м/с, тогда



Способ 2:

Величина возвращающей силы в любой момент времени определяется по закону Гука (см. формулу (1.10)):

.

С учетом формул (1.12) и (1.13), амплитуда силы равна:

.

Амплитуду смещения А и циклическую частоту  определяем из уравнения движения (см. условие задачи):

А = 610^-2 м;  = 10 рад/с.

Тогда



Кинетическая энергия колеблющейся точки определяется по формуле (1.25). Максимальное (амплитудное) ее значение – по формуле (1.27).

С учетом выражения (1.13) получаем:

.