Механика грунтов. Ответы на вопросы. I механика грунтов
 Скачать 0.94 Mb.
|
|
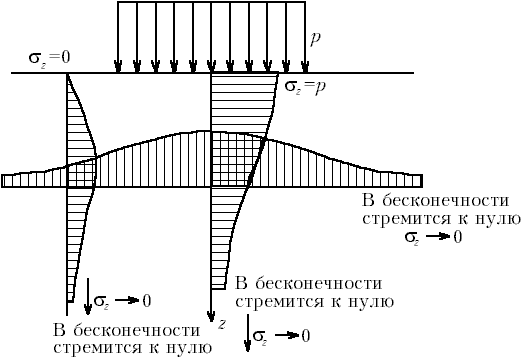
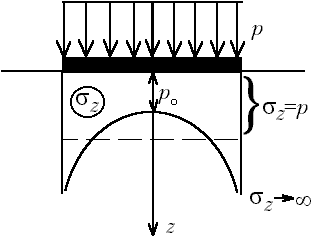
М.8.5. Что такое изолинии напряжений и какой вид имеют изолинии главных напряжений в случае плоской задачи, когда на участке границы полуплоскости приложена равномерно распределенная нагрузка? Изолинии напряжений это линии, во всех точках которых соответствующие напряжения равны. Изолинии главных напряжений, как наибольшего, так и наименьшего, представляются дугами окружностей, проходящих через концевые точки загруженного участка. М.8.6. Какой вид имеют эпюры вертикальных нормальных напряжений z в случае плоской задачи, когда на участке границы приложена равномерно распределенная нагрузка? Эпюры вертикальных нормальных напряжений z изображены на рис. М.8.6.
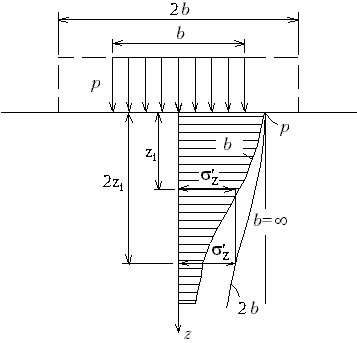
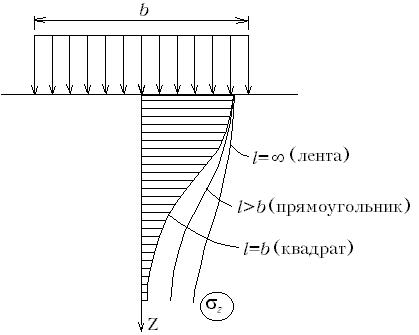
М.8.7. Какие безразмерные координаты приняты в нормах (СНиП) для расчета напряжений? Для расчета напряжений в нормах (СНиП) приняты две относительные координаты и , причем  и  , где b ширина (наименьшая сторона) подошвы прямоугольного фундамента, l его длина (всегда l b). М.8.8. При каком значении , где l длина загруженного участка, b его ширина, считается, что напряжения z в пространственной и в плоской задачах практически можно считать совпадающими? Считается, что при = 10 мы имеем значения напряжений z, которыми для практических целей можно пользоваться и в случае плоской деформации, то есть когда следовало бы считать = . М.8.9. Каким образом, зная эпюру напряжений z вдоль оси z при равномерно распределенной нагрузке, действующей на участке шириной b, построить эпюру z, если нагрузка будет действовать в пределах участка шириной 2b? Как будет трансформироваться эпюра z при дальнейшем увеличении ширины участка, в пределах которого она приложена? Если имеется эпюра напряжений z при ширине загруженного участка b, то, зная ординату z на глубине z, нужно эту же ординату для случая ширины 2b отложить на глубине 2z и т.д. (рис.М.8.9).
При дальнейшем росте ширины загруженного участка напряжения будут все медленнее рассеиваться и при увеличении b до бесконечности эпюра z будет иметь постоянную ординату z p. Все эти эпюры имеют верхнюю ординату, равную p, и выходят поэтому из одной точки.
М.8.11. Каким образом влияет на эпюру z при местной нагрузке наличие жесткого подстилающего слоя? В нижней части эпюры напряжений z , построенных для оси симметрии, вблизи границы жесткого подстилающего слоя происходит так называемая "концентрация" напряжений, то есть их увеличение по сравнению с эпюрой для безграничного снизу слоя (полупространства). Эта концентрация напряжений имеет местное значение и с удалением от границы жесткого подстилающего слоя сравнительно быстро убывает (рис.М.8.11).
М.8.12. Каким образом распределяются напряжения z под подошвой жесткого штампа? Чему равны реактивные напряжения под краем штампа? Чему равны реактивные напряжения под серединой ленточного и круглого жестких штампов?
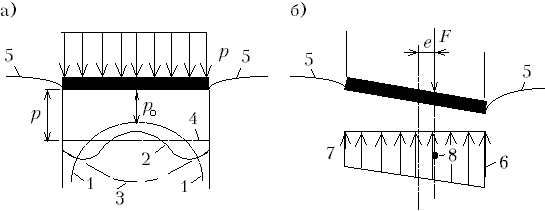
В соответствии с решением задачи об абсолютно жестком штампе, плотно примыкающем к поверхности упругого полупространства и нагруженном симметричной нагрузкой, эпюра реактивных давлений имеет седлообразное очертание с минимальной ординатой в середине и наибольшими ординатами реактивных давлений, равными бесконечности, у краев. Эти бесконечно большие давления у краев штампа вызывают необходимый из постановки задачи "излом" поверхности в краевых точках. Если среднее давление под подошвой штампа равно p, то под серединой ленточного штампа ордината эпюры равна 0,637p (то есть 2p/ ), а под круглым штампом 0,5p (рис.М.8.12). М.8.13*. Что следует сделать, чтобы проверить условие равновесия, пользуясь эпюрой реактивных напряжений под подошвой штампа? Для этой цели следует найти объем эпюры реактивных давлений (для плоского штампа на единицу длины), и этот объем должен равняться суммарной внешней нагрузке, действующей на штамп, то есть сумма проекций на вертикальную ось действующих сил должна равняться нулю (условие равновесия). М.9. РАСЧЕТ ДЕФОРМАЦИЙ ОСНОВАНИЙ СООРУЖЕНИЙ М.9.1. Какой обычно практически считается эпюра приложения нагрузки на основание? Каким образом учитывается заглубление фундамента в основание? Эпюра приложения нагрузки на основание считается обычно равномерной, если нагрузка симметричная, или трапецеидальной, если нагрузка приложена с эксцентриситетом. Заглубление фундамента обычно учитывается в форме равномерной вертикально действующей пригрузки по краям фундамента. М.9.2*. Какой вид имеет эпюра реактивных напряжений под жестким штампом? Каким образом на нее влияют области пластической деформации? Эпюра реактивных напряжений (давлений) под жестким штампом, полученная из решения теории упругости, имеет форму "седла" с максимумом под краями (ординаты равны бесконечности) и минимумом в середине (менее средней величины давления). Поскольку грунт (да и любой материал) не может воспринимать бесконечно больших давлений, то под краями начинают развиваться области пластической деформации, а ординаты эпюры реактивных давлений превышать предельные значения не могут. Но чтобы выполнить условие равновесия, то есть чтобы не нарушался объем (площадь) эпюры, повышаются ординаты эпюры во внутренней ее части (рис.М.9.2,а). В случае эксцентричного приложения внешней нагрузки вместо прямоугольной эпюры мы имеем трапецеидальную (рис.М.9.2,б) и применительно к ней делаются те же построения, какие показаны на рис.М.9.2,а.
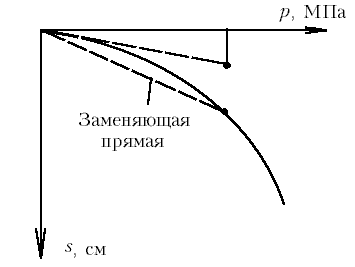
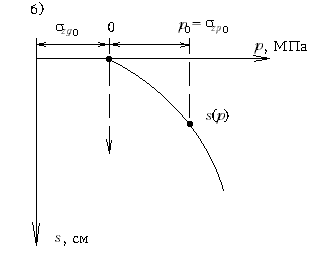
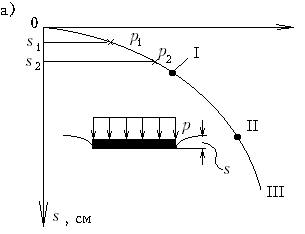
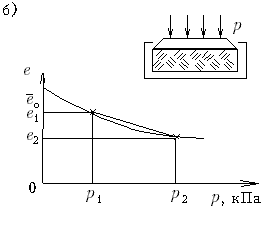
М.9.3. Какой вид имеет кривая зависимости "осадка-нагрузка" для штампа и какой вид ей придают при расчете осадки? Кривая зависимости "осадка-нагрузка" для штампа имеет вид, представленный на графике. При расчете осадки эту кривую на интересующем нас участке заменяют прямой (рис.М.9.3).
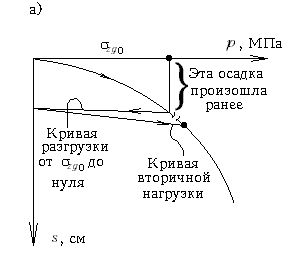
М.9.4. Что называется "осадочным" давлением и какое обоснование дается тому, что осадка рассчитывается не на полную величину давления? Осадочным давлением po именуется разность давлений полного передаваемого основанию через подошву фундамента и "бытового" - природного давления, которое испытывает грунт на отметке заложения подошвы фундамента. Таким образом, осадка рассчитывается не на полную величину прикладываемого давления, а на уменьшенную. Обоснованием для этого служит то, что осадки в грунтовом массиве от веса вышележащей толщи уже завершились, а упругие деформации подъема незначительны, также как и повторные осадки (упругие и остаточные) при нагрузке в пределах давления от вышележащей толщи грунта. Поэтому кривая "осадки-нагрузки" будет иметь вид, показанный на рис.М.9.4.
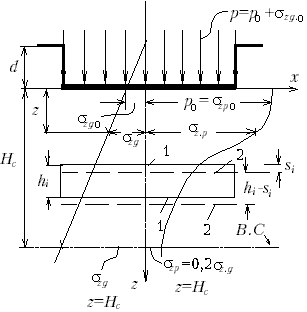
М.9.5. Какие основные допущения заложены в расчете осадки способом послойного суммирования? От какого горизонта отсчитывается эпюра природного давления? Основные допущения следующие: 1. Осадка происходит только при давлениях, превышающих природное давление на отметке заложения подошвы фундамента. 2. Связь между давлением и относительной деформацией линейная и может быть описана зависимостью закона Гука. 3. Напряжения в грунтовом массиве распределяются в соответствии с решениями теории упругости. 4. Рассчитывается эпюра давлений z по глубине только по оси симметрии нагрузки (x = 0), и эти напряжения считаются одинаковыми вдоль горизонтальной оси x. Таким образом, имеет место некоторое завышение напряжений, действующих вдоль оси x, против средних значений в пределах ширины подошвы фундамента. 5. Считается, что грунт не претерпевает бокового расширения и сжимается только в вертикальном направлении (за счет этого осадка несколько преуменьшается). Схема показана на рис.М.9.5.
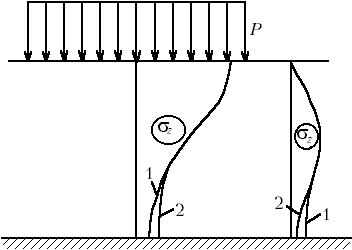
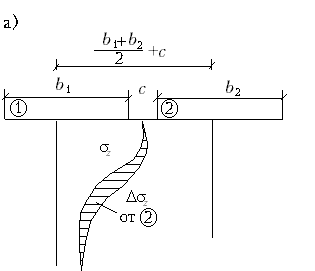
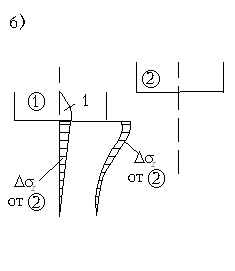
Эпюра природного давления отсчитывается от отметки поверхности грунта от природного рельефа. М.9.6. Какими принимаются боковые давления при расчете осадки способом послойного суммирования? Можно ли считать, что боковое расширение грунта в этом способе полностью не учитывается? При расчете осадки способом послойного суммирования боковые деления принимаются такими, какими они получаются при сжатии грунта в одометре, то есть  Хотя при расчете осадок боковое расширение грунта в этом способе и не учитывается (принимается, что боковые деформации равны нулю), но косвенно они учитываются тем, что распределение напряжений получено из решения теории упругости для полупространства (или полуплоскости), в котором считалось, что среда имела возможность боковых перемещений. Таким образом, оно непосредственно не учитывается, а косвенно и частично учтено. М.9.7. В формуле расчета осадки способом послойного суммирования имеется коэффициент . От чего он зависит? Коэффициент определяется из выражения 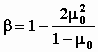 и, следовательно, зависит только от коэффициента Пуассона грунта (коэффициента относительной поперечной деформации). В СНиП 2.02.01-83 условно принято постоянное значение для (считается, что = 0,8). М.9.8. В каких пределах ведется суммирование осадки при расчете методом послойного суммирования? Всегда ли принимается при определении положения нижней границы сжимаемой толщи коэффициент 0,2? В методе послойного суммирования осадки суммируются до той отметки, когда осевые дополнительные по отношению к природным напряжения не снизятся до 20 % от природных (бытовых) на этой же отметке. Эта отметка считается нижней границей сжимаемой толщи (В.С.), а осадками за счет сжатия нижерасположенной толщи пренебрегают. Однако, если ниже расположены слабые грунты с модулем деформации E < 5 МПа, то нижнюю границу сжимаемой толщи следует опустить до той отметки, где дополнительные по отношению к природным давления составят 10 % от природных, а не 20 % как обычно. М.9.9*. Получается ли линейная зависимость осадки от нагрузки в методе послойного суммирования? Нет, не получается в связи с тем, что положение нижней границы сжимаемой толщи изменяется в зависимости от действующего сверху осадочного давления чем больше осадочное давление, тем ниже при прочих равных условиях будет положение нижней границы сжимаемой толщи. Поэтому зависимость осадки от нагрузки не будет линейной. М.9.10. От каких факторов зависит положение нижней границы сжимаемой толщи в методе послойного суммирования (будет ли она располагаться ниже или выше)? Зависит от: удельного веса грунтов основания; наличия горизонта грунтовых вод; заглубления фундамента; нагрузки на фундамент; ширины фундамента; соотношения сторон подошвы фундамента в плане; наличия слоя слабого грунта в основании. М.9.11. Каким образом влияют расположенные рядом фундаменты друг на друга? Как строится эпюра напряжений z при наличии расположенного рядом фундамента? Как поступить, если подошвы соседних фундаментов расположены в разных уровнях? При расположении фундаментов рядом наличие одного из них влияет на осадку соседнего фундамента. Это обстоятельство следует учитывать при расчете осадки (рис.М.9.11). Поэтому к дополнительным давлениям z рассчитываемого фундамента следует добавить значения напряжений z, возникающих в этом месте от соседнего фундамента, пользуясь способом угловых точек. Если отметки подошвы одного и другого фундаментов одинаковы, то эпюра дополнительных давлений будет иметь нулевую ординату вверху. Если соседний фундамент 2 имеет более высоко расположенную подошву, то эпюра получит в уровне подошвы рассчитываемого фундамента 1 конечное значение дополнительного от соседнего фундамента 2 давления z.
М.9.12. Для какого случая получено решение задачи об осадке фундамента, в котором учитывается влияние всех компонентов напряжений? Для однородного изотропного грунта, у которого и модуль деформации E0 и коэффициент Пуассона 0 постоянны. М.9.13. Как вычислить значения модуля деформации грунта E0, необходимые для расчета осадки, по результатам штамповых испытаний в поле или компрессионных испытаний в одометре? На кривой "осадка-нагрузка" штампа выбираются две точки, в пределах которых ведется спрямление. Рекомендуется, чтобы первая точка соответствовала бы давлению в грунте в точке отбора образца от собственного веса вышележащих слоев p1, а вторая соответствовала бы полному давлению p2 от веса грунта и ожидаемой нагрузки от сооружения. Имеется в виду, что кривая в диапазоне выбранных двух давлений хорошо бы аппроксимировалась прямой. Для вычисления модуля деформации E0, МПа, используется формула 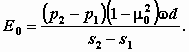 Здесь s2 и s1, см величины осадки, соответствующие давлениям p1 и p, МПа; d диаметр штампа, см; коэффициент формы штампа, равный 0,85; 0 коэффициент Пуассона грунта, принимаемый обычно 0,3 для песков и супесей и 0,4 для глин. По результатам компрессионных испытаний в одометре величина E0, МПа, вычисляется по формуле 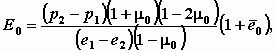 где e1 и e2 значения коэффициентов пористости, соответствующие давлениям p1 и p2;  величина начального коэффициента пористости, получаемая на оси величин e (см.М.4.5, рис.М.9.13).
|
