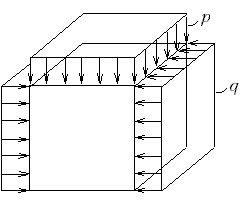
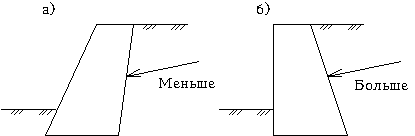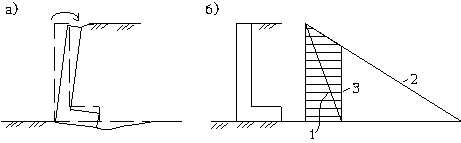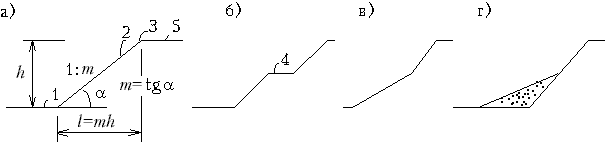Механика грунтов. Ответы на вопросы. I механика грунтов
 Скачать 0.94 Mb. Скачать 0.94 Mb.
|
|
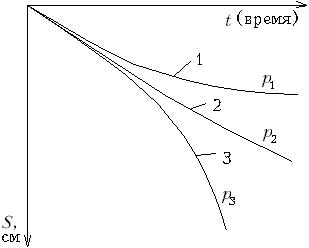
М.12.3. Как деформируется грунт во времени и как выглядит график "осадка-время"? Если взять кубик связного грунта (глины), то при малых давлениях, прикладываемых к нему сверху, происходит затухание осадки со временем и ее стабилизация (фаза затухающей ползучести 1) (рис.М.12.3). При дальнейшем увеличении нагрузки осадка будет нарастать практически с постоянной скоростью и не стабилизироваться (фаза установившейся ползучести 2). Дальнейший рост нагрузки приведет к такому состоянию, когда скорость нарастания осадки со временем будет расти и, наконец, произойдет полное разрушение грунта. Это - фаза прогрессирующего течения 3.
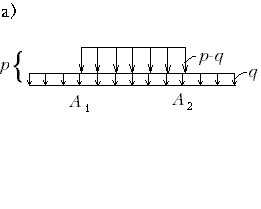
М.12.4. Назовите фазы деформирования и где находятся границы этих фаз на графике "осадка нагрузка"? 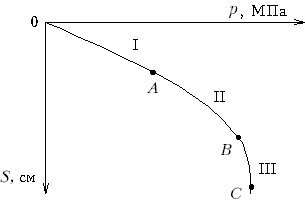 На кривой "нагрузка-осадка" (рис.М.12.4), полученной для штампа, находящегося на поверхности основания, можно различить три фазы: I фазу уплотнения, II фазу образования зон сдвигов, размер которых растет с ростом нагрузки и III фазу полного выпирания (потеря несущей способности основанием). М.12.5. Какая схема принимается для определения границы I фазы? Какой коэффициент бокового давления грунта в условиях естественного залегания 0 принимается в схеме Пузыревского-Герсеванова? Если 0 1, будет ли зарождение пластической области происходить раньше или позднее? Для определения границы I фазы принимается схема, когда основание загружено равномерно распределенной нагрузкой p, расположенной на участке шириной b. По бокам действует пригрузка q, а область предельного равновесия только начинает образовываться в точках A1 и A2. Коэффициент бокового давления 0 в схеме Пузыревского-Герсеванова принимается равным единице ( 0 = 1). Если 0 < 1 или 0 > 1, то в обоих случаях область пластической деформации будет зарождаться раньше, чем при 0 = 1 (рис.М.12.5).
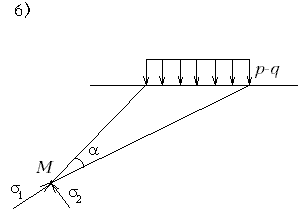
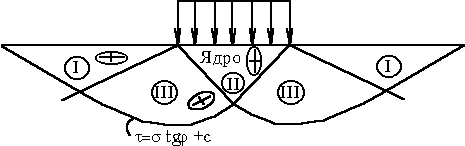
М.12.6. Какой вид имеют формулы для главных напряжений при загрузке конечного участка границы полуплоскости равномерно распределенной нагрузкой? Формулы для главных напряжений наибольшего 1 и наименьшего 2 имеют следующий вид: где угол видимости (см.рис.М.12.5). М.12.7. Принимаются ли для расчета первой критической нагрузки полные значения напряжений, в которых учитывается собственный вес грунта, или только дополнительные напряжения от внешней нагрузки? При выводе формулы для первой критической нагрузки принимаются полные значения напряжений, представляющие собой суммарные напряжения от внешней нагрузки р, пригрузки q и веса грунта в рассматриваемой точке на глубине z, равные z. Напряжения считаются передающимися по гидростатичекому закону как от веса z, так и от пригрузки q, т.е. как от тяжелой жидкости. Поэтому считается, что 0 = 1. М.12.8. Какое ставится экстремальное условие, чтобы получить недостающее уравнение для определения величины первой критической нагрузки? Экстремальное условие заключается в том, что надо найти такое значение угла видимости , чтобы при нем глубина расположения точки с предельным состоянием z была бы максимальной, то есть производная М.12.9. Какой вид имеет обобщенная формула Пузыревского-Герсеванова? В виде скольких слагаемых ее можно представить? Чему равны коэффициенты формулы M ,Mq,Mc и от чего они зависят? Чему равна величина zmax по Пузыревскому-Герсеванову и по СНиП? Обобщенная формула Пузыревского-Герсеванова имеет следующий вид 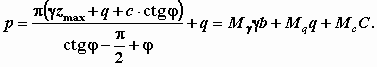 Коэффициенты равны 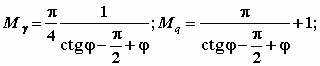 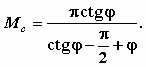 При выводе коэффициента Мсогласно СНиП принимается zmax=b/4, коэффициенты М, Мq и Мc зависят только от угла внутреннего трения грунта . У Герсеванова и Пузыревского было принято, что zmax= 0. М.12.10. Каким образом происходит процесс развития областей пластических деформаций под фундаментом с ростом нагрузки? 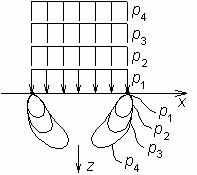 Считатется, что области пластических деформаций зарождаются у краев фундамента; далее с ростом нагрузки они распространяются вглубь и начинают заходить под фундамент (рис.М12.10). Наконец, при нагрузке, достигающей несущей способности основания, обе области пластических деформаций смыкаются на оси фундамента и происходит резкое проседание его вниз. М.12.11*. Какой вид имеет схема расчета несущей способности основания "по Прандтлю"? Что называется "упругим ядром" и где оно находится? При расчете величины несущей способности "по Прандтлю" предполагается существование трех зон: зоны с максимально напряженным состоянием I (или зоны пассивного давления), зоны с минимально напряженным состоянием II (или зоны активного давления) и переходной между ними зоны III, позволяющей получить плавное изменение напряжений без скачков в них. При этом предполагается, что нагрузка является равномерной и не имеет горизонтальной составляющей. В действительности мы прикладываем нагрузку с помощью жесткого шероховатого штампа, поэтому непосредственно под ним вместо зоны с минимально напряженным предельным состоянием формируется зона, в которой нет предельного состояния и которая как бы сливается со штампом, составляя с ним одно целое. Эта зона называется "упругим" или "жестким" ядром (рис.М.12.11).
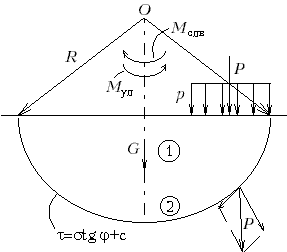
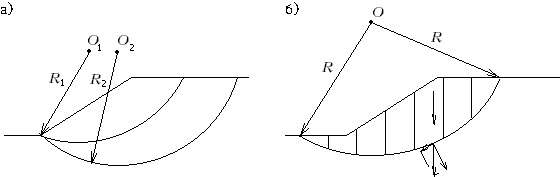
М.12.12. Какое условие, связывающее напряжения, следует ставить на линии, ограничивающей область выпирания? На этой линии ставится условие Кулона М.12.13. Большее или меньшее значение имеют коэффициенты N , Nq и Nc в формуле несущей способности, чем соответственно коэффициенты М , Мq и Мc в обобщенной формуле Герсеванова-Пузыревского и от чего они зависят? Поскольку коэффициенты М , Мq и Мcотвечают лишь незначительным по размерам областям пластической деформации, а соответственные им коэффициенты N , Nq и Nc полному раскрытию этих областей, то, естественно, последние больше по своим значениям, чем первые. И те и другие зависят от угла внутреннего трения , а если нагрузка имеет кроме вертикальной еще и горизонтальную составляющую, то и от угла наклона равнодействующей к вертикали. Максимальное значение всех коэффициентов мы получаем, если нет горизонтальной составляющей. М.12.14. Какая основная идея положена в основу метода круглоцилиндрических поверхностей? В основе этого метода заложена идея о том, что при разрушении основания под фундаментом возникают две жесткие непредельные области, отделяющиеся друг от друга круглоцилиндрической поверхностью (рис.М.12.14). При предельных условиях одна (верхняя) область 1 скользит вдоль этой поверхности по другой нижней области 2. Благодаря условию, что обе области жесткие, возможно осуществление переноса действующих сил вдоль линий их действия и оперирование равнодействующими. Наиболее опасная круглоцилиндрическая поверхность находится путем пробного поиска и определения минимальной величины отношения момента всех удерживающих сил к моменту сдвигающихся сил.
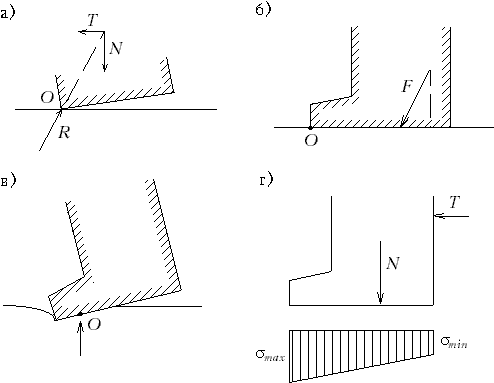
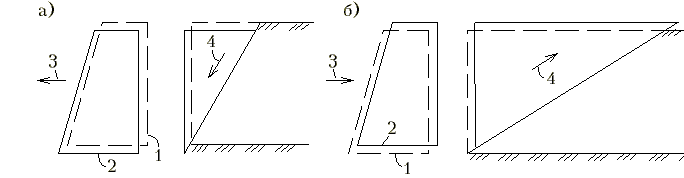
12.15*. Какие уравнения удовлетворяются и какие не удовлетворяются в способе круглоцилиндрических поверхностей? В способе круглоцилиндрических поверхностей полностью не удовлетворяются условия равновесия для проекций на оси (вертикальную и горизонтальную), так как нормальная по отношению к дуге окружности составляющая равнодействующей нагрузки умножается на коэффициент внутреннего трения и этим она переводится в касательную компоненту, в то время как фактически вдоль поверхности мобилизуется не все трение, а только часть его. То же самое делается и с силами сцепления, действующими вдоль потенциальной поверхности скольжения, которые мобилизуются лишь частично. Поэтому этот способ следует рассматривать как инженерный и недостаточно строгий. М.12.16. Какой вид имеет формула для коэффициента запаса (надежности)? Зависит ли коэффициент запаса устойчивости на сдвиг от радиуса окружности скольжения? Эта формула для способа круглоцилиндрических поверхностей имеет следующий вид: 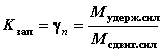 . .От радиуса отношение моментов сил, входящих в эту формулу, формально не зависит, однако когда отыскивается минимальное значение величины Kзап= n, то устанавливаются и радиус, и положение центра дуги, отвечающие условию этого минимума. М.12.17*. Каким образом рассчитывается устойчивость на сдвиг по плоскости контакта сооружения с основанием? 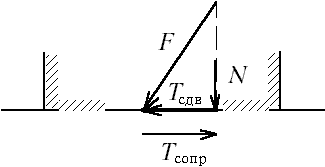 Если не учитывается величина отпора грунта со стороны, куда направлен сдвиг, то подсчитывается вертикальная составляющая действующих сил N (рис.М.12.17), затем она умножается на коэффициент трения f и добавляются силы сцепления по контакту C. После этого получившееся максимально возможное значение силы сопротивления делится на величину сдвигающей силы Tсдв и тем самым находится величина коэффициента запаса (надежности), то есть М.12.18. Каким образом рассчитывается устойчивость сооружения на опрокидывание? Устойчивость на опрокидывание (рис.М.12.18,а) оценивается по отношению моментов сил удерживающих и сил опрокидывающих, взятых относительно крайней точки. При этом считается, что сооружение как бы чуть приподнялось и поэтому реакция основания в виде сосредоточенной силы приложена в крайней точке, а, следовательно, в условие равновесия моментов она не войдет, так как проходит через этот полюс. Для того, чтобы увеличить устойчивость на опрокидывание, следует ввести слева у сооружения консоль (рис.М.12.18,б). В случае деформируемости основания вращение при опрокидывании происходит не вокруг одной крайней точки, а сооружение "входит" в грунт основания, поэтому и вращение произойдет вокруг центра, располагающегося в пределах подошвы сооружения (рис.М.12.18,в). Опрокидыванию предшествует крен сооружения. Обычно стремятся не допускать отрыва подошвы от грунта, кроме особых случаев (например, действия сейсмических сил), и ограничивать соотношение между максимальным и минимальным вертикальными напряжениями (рис.12.18,г). При установлении величин этих максимальных напряжений следует учитывать также и касательные усилия, возникающие по подошве сооружения.
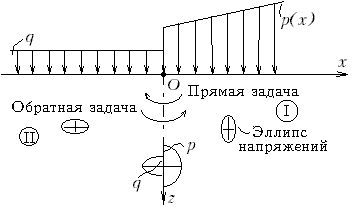
М.13. ТЕОРИЯ ПРЕДЕЛЬНОГО РАВНОВЕСИЯ ГРУНТОВ М.13.1. Каким образом записывается условие предельного равновесия в главных напряжениях? Каким образом это условие преобразуется в зависимость, в которую входят все три компонента напряжений (в декартовых координатах)? Условие предельного равновесия в главных напряжениях имеет вид С помощью круга Мора и теоремы Пифагора, согласно которой 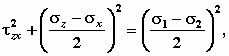 а также учитывая, что М.13.2*. Сколько неизвестных компонентов напряжений мы имеем в случае плоской задачи, осесимметричной задачи, пространственной задачи в общем случае? В случае плоской задачи мы имеем три неизвестных компонента напряжений, в случае осесимметричной задачи четыре, а для пространственной задачи в общем случае шесть компонентов напряжений. М.13.3*. Какие дополнительные зависимости привлекаются к уравнениям равновесия в теории предельного равновесия сыпучей среды в плоской, осесимметричной и пространственной задачах и сколько этих дополнительных зависимостей? К двум уравнениям равновесия в случае плоской задачи привлекается одно условие, связывающее компоненты напряжений, условие предельного равновесия. В случае осесимметричной задачи к двум уравнениям равновесия (проекции на оси координат) привлекается также одно условие предельного равновесия, а дополнительным, поскольку компонентов в уравнениях четыре, является условие равенства между собой двух главных напряжений (промежуточное равно минимальному или максимальному). В случае пространственной задачи мы имеем три уравнения равновесия и одно уравнение предельного равновесия - таким образом, не хватает двух уравнений. М.13.4*. В каких случаях общая система уравнений теории предельного равновесия является замкнутой? В каких случаях и сколько уравнений не хватает для получения замкнутости системы? Что называется условием "полной" и "неполной" сыпучести? В случае плоской задачи система оказывается полностью замкнутой. В случае осесимметричной задачи не хватает одного уравнения и привлекается условие "полной сыпучести" путем приравнивания промежуточного главного напряжения минимальному или максимальному, после чего система становится замкнутой. Если не привлечь этого условия, то система будет незамкнутой (неполной). В случае пространственной задачи не хватает двух уравнений и система оказывается незамкнутой. М.13.5*. Чему равен порядок системы дифференциальных уравнений в частных производных? Какой порядок имеет система дифференциальных уравнений теории упругости (плоская задача) и теории предельного равновесия сыпучей среды? Порядок системы дифференциальных уравнений в частных производных равен сумме порядков входящих в нее уравнений. Система дифференциальных уравнений теории упругости имеет четвертый порядок, а система уравнений теории предельного равновесия второй порядок, так как уравнение предельного равновесия включает только компоненты напряжений, но не их производные. Это уравнение второй степени, но нулевого порядка. М.13.6. Что дают нам произвольные постоянные интегрирования и произвольные функции интегрирования, получаемые в результате решения основной системы уравнений теории упругости и теории предельного равновесия сыпучей среды? Произвольные постоянные интегрирования позволяют из общего решения системы обыкновенных дифференциальных уравнений получить частное решение, удовлетворяющее краевым условиям. Произвольные функции, получающиеся в результате интегрирования системы дифференциальных уравнений в частных производных, позволяют получить частное решение, удовлетворяющее граничным условиям рассматриваемой задачи. В теории упругости и в теории предельного равновесия это напряжения на границе области. Вдоль участка границы возможно задать два граничных условия в теории предельного равновесия это нормальное и тангенциальное напряжения на границе. В теории упругости граничные условия могут быть заданы в напряжениях или перемещениях, могут быть и смешанного типа. М.13.7*. Чем отличаются дифференциальные уравнения гиперболического, параболического и эллиптического типов? Что называется характеристикой дифференциального уравнения и как ее найти? Сколько существует характеристик? Характеристикой дифференциального уравнения называется линия на плоскости, вдоль которой частные производные не могут быть однозначно определены (детерминант оказывается равным нулю). Характеристики системы дифференциальных уравнений могут быть найдены путем приравнивания всех детерминантов системы нулю. Система гиперболического типа (теория предельного равновесия сыпучей среды) имеет два семейства действительных характеристик, система параболического типа (теория фильтрационной консолидации) одно и система эллиптического типа (теория упругости) два семейства мнимых характеристик. М.13.8*. С чем совпадают характеристики системы дифференциальных уравнений теории предельного равновесия сыпучей среды? Сколько систем характеристик мы имеем в плоской задаче теории предельного равновесия? Характеристики системы дифференциальных уравнений теории предельного равновесия сыпучей среды совпадают с линиями скольжения. В плоской задаче мы имеем два семейства характеристик, следовательно, два семейства линий скольжения, вдоль которых выполняется условие М.13.9. Каким образом решаются уравнения теории предельного равновесия сыпучей среды? Уравнения теории предельного равновесия сыпучей среды в общем случае решаются численным способом, поскольку система эта нелинейная (в условие предельного равновесия напряжения входят в квадрате). Лишь очень ограниченное количество задач может быть решено в конечном виде. М.13.10*. Всем ли граничным условиям может удовлетворять система уравнений теории предельного равновесия сыпучей среды? Нет, не всем. Не все граничные условия могут обеспечить такое напряженное состояние, при котором в каждой точке выполняется предельное условие. Поскольку основная система имеет второй порядок и произвольных функций интегрирования две (а в теории упругости их четыре), этих двух функций "не хватает", чтобы удовлетворить любым граничным условиям. М.13.11. Как ставятся конкретные задачи в теории предельного равновесия сыпучей среды? Конкретные задачи ставятся следующим образом: на одной части границы области заданы напряжения по величине и по направлению. Требуется отыскать величину (при заданном направлении действия) или направление (при заданной величине) напряжений на соседней части границы области, исходя из того, что в каждой точке области имеет место предельное состояние. М.13.12*. Имеется ли единственность в постановке задач в теории предельного равновесия сыпучей среды и в теории упругости? В теории предельного равновесия такой единственности нет, поскольку основным уравнением предельного равновесия является квадратное уравнение относительно напряжений. Поэтому имеет место двойственность, и правильную постановку задачи подсказывают результаты экспериментальных исследований. В теории упругости вся система линейная, поэтому имеет место единственность решения задач. М.13.13. Какие простейшие задачи теории предельного равновесия сыпучей среды решаются в замкнутом виде? Простейшие задачи, решаемые в теории предельного равновесия в замкнутом виде, это задачи об активном и пассивном давлениях грунта на подпорную стену при ее гладкой вертикальной поверхности, примыкающей к засыпке, и при горизонтальной поверхности грунта засыпки. Также решается задача о грунтовой трубе, находящейся в предельном состоянии под действием давления изнутри (или снаружи). Имеются еще некоторые задачи, но число их весьма ограничено. М.13.14. Каким образом влияет удельное сцепление в зоне простейшего напряженного состояния на боковые напряжения x при заданном напряжении z? В зоне минимального напряженного состояния (зоне активного давления) величина x с ростом сцепления c уменьшается, а в зоне максимального напряженного состояния (зоне пассивного давления) величина x с ростом сцепления c увеличивается. М.13.15*. Откуда произошло название зон с простейшим напряженным состоянием зоны минимально напряженного состояния и зоны максимально напряженного состояния? Зона минимального напряженного состояния называется так потому, что эллипс напряжений в ней имеет наименьшую ось горизонтальной и быть "тоньше" не может (при той же вертикальной оси). Зона максимального напряженного состояния имеет "лежачий" эллипс напряжений и горизонтальная ось эллипса быть больше не может (при той же вертикальной оси). Таким образом, горизонтальная ось эллипса при неизменной вертикальной оси определяет эти названия. М.13.16. В чем заключается постановка прямой и обратной задач теории предельного равновесия сыпучей среды? В прямой задаче об основании задана нагрузка по величине и направлению и отыскивается величина пригрузки (при заданном ее направлении) или направление (при заданной ее величине). В обратной задаче об основании задана пригрузка (по величине и направлению) и отыскиваются величина нагрузки (при заданном ее направлении) или ее направление (при заданной величине). Таким образом, три условия всегда оказываются заданными, а одно подлежит определению. М.13.17*. Для чего нужна переходная зона между зонами с максимальным и минимальным напряженными состояниями в задачах теории предельного равновесия сыпучей среды? Включение в рассмотрение переходной зоны (зона III на рис.М.12.11) позволяет получить непрерывность всех компонентов напряжений при переходе из одной зоны в другую и плавный поворот осей эллипсов напряжений. М.13.18*. Чем отличаются разрывное и неразрывное решения и какие компоненты напряжений претерпевают разрыв? Разрывное и неразрывное решения задачи об основании дают резко различную величину несущей способности. В этой задаче при переходе от зоны с минимальным напряженным состоянием к зоне с максимальным напряженным состоянием претерпевает разрыв на границе зон вертикальное напряжение z, а напряжение x является непрерывным (в обеих зонах xz = 0).
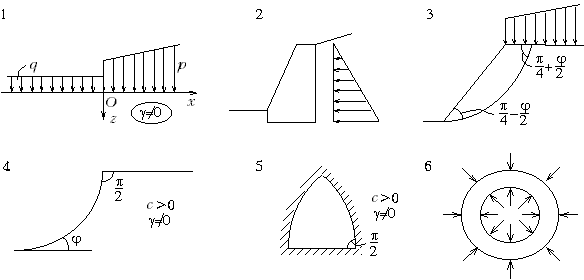
М.13.19. Какой вид имеет формула несущей способности по Прандтлю и что получается, если среда не обладает трением ( =0)? Формула несущей способности p, кПа, по Прандтлю (в ней рассматривается сыпучая среда) имеет следующий вид: где q пригрузка, кПа. При разрывном решении эта формула выглядит так: 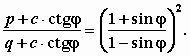 Если среда не обладает трением, то из первой формулы получим (по Прандтлю) а из второй М.13.20*. Где располагается "особая точка" и каковы ее свойства? "Особая точка" (cм.рис.М.13.18, точка О) располагается в месте, где кончается нагрузка и начинается пригрузка, то есть имеет место скачок в величине усилий, приложенных на границе. Особая точка обладает тем свойством, что при подходе к ней по различным лучам мы получаем различие напряжения от наибольшего (нагрузка) до наименьшего (пригрузка). Таким образом, в особой точке имеет место многозначность напряжений. М.13.21. Нужны ли эксперименты для правильной постановки задачи с использованием основных уравнений теории предельного равновесия сыпучей среды? Да, нужны не только для проверки получаемых величин напряжений, как обычно, но и для постановки, связанной с неоднозначностью (двойственностью) решений теории предельного равновесия сыпучей среды. М.13.22. Какие инженерные задачи рассматриваются в теории предельного равновесия сыпучей среды? В теории предельного равновесия обычно рассматриваются следующие задачи (рис.М.13.22) с целью определения: 1) несущей способности основания (зависимости нагрузки от пригрузки или наоборот); 2) давления грунта на подпорную стенку активного и пассивного; 3) устойчивости откоса заданного очертания (необходимой пригрузки сверху, обеспечивающей предельное состояние); 4) формы предельно устойчивого откоса; 5) формы свода обрушения связного грунта при подземной проходке; 6) предельного давления в грунтовой трубе.
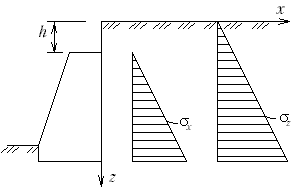
М.13.23. Какова предельная высота вертикального откоса? Как ее найти? По теории предельного равновесия неподкрепленный вертикальный откос может иметь высоту h не более где - удельный вес грунта. Эта высота находится из условия, что в самой нижней точке такого откоса горизонтальное напряжение x = 0, а вертикальное z= h. Для решения задачи используется условие предельного равновесия (рис.М.13.23).
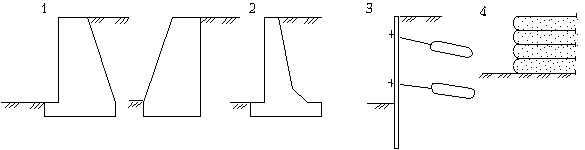
М.13.24. Каков предельный угол наклона сыпучего откоса? Предельный угол наклона сыпучего откоса равен углу внутреннего трения . М.13.25. Какую форму имеет предельно устойчивый откос без пригрузки? Какие условия ставятся на его контуре? 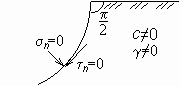 На контуре откоса рис.М.13.25 касательное напряжение n и нормальное напряжение n должны быть равны нулю. М.13.26. Что означает термин "отрицательная пригрузка" в задаче о несущей способности основания? "Отрицательная пригрузка" означает, что для обеспечения предельного состояния во всех точках массива грунта необходимо приложить на границе не сжимающие, а растягивающие напряжения, то есть "тянуть вверх", что не реально. Поэтому не во всей области основания практически возможно обеспечить предельное состояние. М.14. РАСЧЕТ ДАВЛЕНИЯ ГРУНТОВ НА ОГРАЖДЕНИЯ М.14.1. С какой целью применяются подпорные стены? Подпорные стены применяются для удержания грунтовых массивов от сползания в том случае, когда устройство искусственного откоса невозможно, а естественный склон необходимо удерживать от сползания. М.14.2. Чем гравитационные подпорные стены отличаются от облегченных гибких подпорных стен? При гравитационных подпорных стенах (рис.М.14.2) устойчивость на сдвиг обеспечивается их весом (весом материала стены и грунта, находящегося над подошвой стены), а горизонтальная составляющая давления земли воспринимается силой трения, развивающейся в плоскости подошвы стены. Облегченные гибкие стены заделываются в основание и их устойчивость на сдвиг обеспечивается развитием пассивного отпора в нижней части, а также возможным наличием анкерной заделки в верхней части стены.
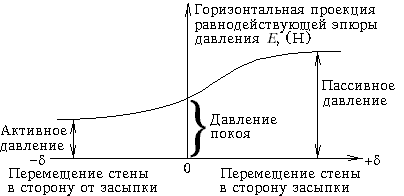
М.14.3. Какой вид имеет диаграмма давления на стену в зависимости от ее поступательного перемещения? Диаграмма давления, возникающего между засыпкой и задней гранью стены, показана на рис.М.14.3.
Активное давление минимально возможное давление, пассивное максимально возможное давление. М.14.4. Что называется активным давлением грунта на стену и когда оно проявляется? Активным называется минимальное из всех возможных для данной стены давление на нее грунта, проявляющееся в том случае, если стена имеет возможность переместиться в сторону от засыпки под действием давления грунта. Активное давление иногда называется распором (рис.М.14.4,а)
М.14.5. Что называется пассивным давлением грунта на стену и когда оно проявляется? Пассивным называется максимальное из всех возможных для данной стены давление ее на грунт, проявляющееся в том случае, если стена имеет возможность перемещаться в сторону засыпки под действием внешних сил. Пассивное давление называется отпором (рис.М.14.4,б). М.14.6. Что называется "давлением покоя" и когда оно проявляется? Давлением покоя называется такое давление грунта на стену, которое соответствует нулевому ее перемещению, то есть это такое боковое давление, которое имеет место в массиве грунта, когда стены нет, а поверхность грунтового массива горизонтальна. М.14.7. Какие усилия действуют на подпорную стену и как рассчитывается ее устойчивость? На подпорную стену действует давление грунта и давление воды. Если над засыпкой имеется пригрузка, то она создает дополнительное усилие, действующее на стену. В расчете учитывается также вес стены и лежащего непосредственно над ее подошвой грунта. В связи с заглублением стены в грунт может быть учтено действующее с противоположной засыпке стороны пассивное давление (отпор), хотя это обстоятельство в запас устойчивости часто не учитывается. Если на стену постоянно действуют усилия со стороны лицевой грани, то они также принимаются в расчет. М.14.8. Каким образом из уравнения предельного равновесия получить эпюру давления грунта на гладкую подпорную стену и действующее усилие? Показать двойственность решения. Уравнение предельного равновесия, записанное в декартовых координатах, имеет вид 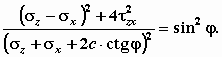 Рассматривая простейшее напряженное состояние, соответствующее гладкой без трения подпорной стене и горизонтальной поверхности засыпки, когда zx = 0, и извлекая корень из обеих частей этого уравнения, получим 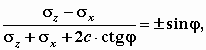 то есть линейное уравнение относительно напряжений z и x. Напряжение z полагается равным z. Находятся напряжения x. , то есть ординаты эпюр давления грунта на подпорную стену. М.14.9. Каким образом влияет на величину активного и пассивного давлений на стену удельное сцепление в грунте? При одинаковом не изменяющемся значении угла внутреннего трения с увеличением удельного сцепления в грунте c активное давление уменьшается, а пассивное увеличивается. М.14.10*. Каким образом влияет на величину равнодействующей активного давления грунта на подпорную стену наклон задней грани стены? Если задняя грань стены имеет уклон в сторону засыпки, то давление уменьшается (рис.М.14.10,а), в противоположную сторону увеличивается (рис.М.14.10,б).
М.14.11*. Каким образом влияет на величину равнодействующей активного давления грунта на подпорную стену увеличение шероховатости задней грани? С ростом шероховатости поверхности стены, как правило, активное давление уменьшается, а пассивное увеличивается. М.14.12. В чем суть предложений Кулона по расчету давления грунта на подпорную стену? По Кулону призма обрушения всегда ограничивается плоскостью (а не криволинейной поверхностью), как по теории предельного равновесия в общем случае. Далее разыскивается экстремальный случай (наклон этой плоскости) из условия максимума для активного давления и минимума для пассивного давления. М.14.13. Какими конструктивными приемами при одинаковом объеме материала стены можно увеличить ее общую устойчивость на сдвиг и опрокидывание? 1. Часть материала гравитационной стены заменить грунтом, чтобы создать необходимый вес. 2. Устроить дренаж в засыпке. 3. Засыпку провести грунтом с возможно большим углом внутреннего трения. 4. Со стороны лицевой грани стены сделать выступ - консоль (против опрокидывания). 5. Заднюю грань стены наклонить, чтобы стена лежала на грунте. М.14.14. Какой вид имеет эпюра реактивных давлений под подошвой стены и с помощью какого приема ее можно сделать более равномерной? Для какой цели нужно иметь более равномерную эпюру реактивных давлений? Эпюра реактивных давлений принимается линейной (трапеция). Более равномерной ее можно сделать, увеличив выступ консоли у лицевой стороны стены. Чем равномернее эпюра давлений, тем меньше вероятность перекоса стены вследствие осадки грунта основания. М.14.15*. Что представляет собой явление "навала" подпорной стены на грунт и от чего он возникает? Всегда ли следует его учитывать? Явление "навала" подпорной стены на грунт связано с ее неравномерной осадкой и наклоном задней грани вследствие этой осадки в сторону засыпки (рис.М.14.15). В результате давление становится больше активного и это обстоятельство следует учитывать при расчете самой стены на прочность. Навал стены целесообразно учитывать только при высоких подпорных стенках.
М.14.16. Какой вид приобретает эпюра активного давления грунта с учетом явления "навала" и после трамбования засыпки? Использование какого грунта для засыпки уменьшает активное давление на стенку? С учетом навала эпюра давления увеличивается и занимает промежуточное положение между эпюрой активного и пассивного давления (см. рис.М.14.15,б). Практически давление увеличивается до 10-15 % (на высокую стену). Такое же изменение в эпюре вызывает уплотнение засыпки трамбованием (этот эффект учитывается на глубину уплотнения). Чем больше угол внутреннего трения в грунте засыпки, тем меньше активное давление. Поэтому использование крупнообломочного грунта или крупного песка приводит к уменьшению активного давления грунта. М.14.17*. Почему нужен дренаж за стеной и каким образом влияет наличие воды в засыпке на общее активное давление грунта на стену? Дренаж за стеной нужен потому, что он снимает давление воды на стену и уменьшает фильтрационное противодавление на подошву грунта. При наличии дренажа увеличивается устойчивость стены. Несмотря на то, что в случае обводнения грунт "становится легче" за счет взвешивания скелета в воде, давление воды больше, чем это "облегчение", и суммарное давление обводненного грунта на стену больше, чем необводненного. Ординаты эпюры давления x при гладкой стене и горизонтальной засыпке равны Здесь второе слагаемое зависит от давления воды. М.14.18*. Каким образом отличается давление грунта на стену "по Кулону" от давления по теории предельного равновесия (активное и пассивное)? Активное давление может быть равно давлению "по Кулону" или быть больше его (на несколько процентов). Пассивное давление может быть равно давлению "по Кулону" или резко превышать его (в отдельных случаях даже в три раза). М.14.19*. Какие предположения делаются при расчете гибких подпорных стен? Что такое "коэффициент постели"? При расчете гибких подпорных стен предполагается, что ордината эпюры бокового давления грунта на стену связана с прогибом стены в этом месте чем больше прогиб, тем меньше давление. Коэффициент постели это коэффициент пропорциональности между перемещением и давлением, имеющий размерность, совпадающую с размерностью удельного веса. М.14.20*. Как рассчитывается подпорная стена с ломаной задней гранью? Cтена продолжается до верха и рассчитывается как будто наклон задней грани всюду одинаков, а затем из этой эпюры используется только та часть, которая приходится на фактически существующий участок стены. В целом эпюра получается ломаной. М.15. ОТКОСЫ М.15.1. Что называется откосом? Откосом называется искусственно созданная наклонная поверхность, ограничивающая естественный грунтовый массив или насыпь. М.15.2. Что такое заложение откоса? Где находится бровка откоса? Для чего устраиваются бермы? Заложение откоса это горизонтальная его проекция. Бровка откоса - линия, которая находится там, где начинается горизонтальная часть его гребень. Бермы горизонтальные площадки, которые устраиваются для общего уположения откоса, а также по технологическим обстоятельствам (рис.М.15.2).
М.15.3. От каких факторов зависит устойчивость откосов? Устойчивость откосов зависит от: прочности грунтов под откосом и в его основании, причем характеристики прочности могут изменяться со временем; удельного веса грунтов под откосом и в его основании; крутизны откоса; высоты откоса; нагрузок на поверхности откоса; фильтрации воды через откос; положения уровня воды, насыщающей грунт в теле откоса. Откосы земляных плотин и дамб в подводной части обычно более пологие, чем в надводной. М.15.4. Какой характер может носить разрушение откоса? Разрушение откоса может происходить внезапно и носить характер обвала или оплыва, а также проявляться в виде длительного оползания, что особенно характерно для глинистых грунтов. В ряде случаев грунты оснований под откосом являются менее прочными, чем грунты в теле откоса. Тогда становится возможным их выдавливание из-под откоса, с обрушением всего откоса или его части. М.15.5. Какие основные причины могут вызвать нарушение устойчивости откосов? Какими мероприятиями можно увеличить устойчивость откосов? Возможные причины нарушения устойчивости откоса: излишняя его крутизна; подрезка откоса в нижней части; утяжеление откоса вследствие увлажнения грунта; уменьшение величины прочностных характеристик грунта тела откоса вследствие увлажнения или других обстоятельств; нагрузка на гребне откоса; динамическое воздействие и т.д. Мероприятия по увеличению общей устойчивости: 1) уположение откоса (рис.М.15.2,б); 2) пригрузка его нижней части (рис.М.15.2,г); 3) дренирование откоса; 4) закрепление грунтов тела откоса; 5) применение свай; 6) устройство подпорной стены и т.д. Укрепление поверхности откоса может быть достигнуто устройством одежды, высевом трав с прочной корневой системой и т.д. М.15.6. Какой откос называется предельно устойчивым? Предельно устойчивым называется откос, под которым в каждой точке грунт находится в предельно напряженном состоянии. Теоретически предельно устойчивый откос из сыпучего грунта песка имеет прямолинейный контур с углом наклона к горизонту, равным углу внутреннего трения. Предельно устойчивый откос из связного глинистого грунта криволинейный (см.рис.М.13.25), книзу он постепенно уполаживается и стремится к наклону, приближающемуся к углу внутреннего трения. Наиболее рациональное очертание откоса близкое к предельно устойчивому. М.15.7. Каким образом проводится расчет устойчивости откосов по методу круглоцилиндрических поверхностей? Как рассчитать разнородный откос по методу круглоцилиндрических поверхностей? По методу круглоцилиндрических поверхностей проводится серия возможных дуг окружностей и для каждой из них составляется отношение моментов удерживающих и сдвигающих сил. Далее отыскивается методом пробных поисков минимум этого отношения. В том случае, если откос разнородный, то зона, ограничиваемая поверхностью откоса и дугой проведенной окружности, делится на вертикальные равные по ширине отсеки, а для каждого из них составляются величины моментов удерживающих и сдвигающих сил. Далее моменты удерживающих и сдвигающих сил отдельно суммируются и отыскивается их отношение, которое называется коэффициентом надежности. Следующий заключительный этап поиск минимального значения коэффициента надежности (рис.М.15.7).
М.15.8. Каким образом отыскиваются положение центра и радиус дуги окружности, по которой наиболее вероятно скольжение в откосе? Отыскивается такая дуга окружности, для которой отношение моментов сил удерживающих и сил сдвигающих минимально. Для этой цели берется не менее девяти положений центров дуг, а затем графически отыскивается минимальное значение отношения этих моментов. М.15.9. В каких случаях можно обойтись без расчетов устойчивости откосов? Расчет устойчивости откосов обязательно делается при их высоте более 5 м. Однако при неблагоприятных условиях следует проводить проверку устойчивости откосов и при меньших их высотах, например при наличии фильтрующейся воды, слоистого напластования грунтов с падающими слоями и др. Крутизна невысоких до 5 м откосов при благоприятных условиях обычно нормируется по виду и состоянию грунтов, а также высоте откосов из условий техники безопасности. М.15.10. Что такое "прислоненный откос" и каковы предпосылки его расчета? 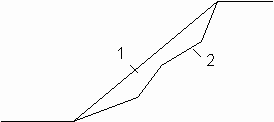 Прислоненный откос покоится обычно на более плотном и крепком грунте (рис.15.10). Поэтому поверхностью скольжения служит контур поверхности более прочного грунта. Составляется условие равновесия массы грунта, которая может сползти, и вычисляется отношение суммарных сил, удерживающих откос и вызывающих его сползание. Это отношение и явится коэффициентом надежности. М.16. ДИНАМИЧЕСКИЕ СВОЙСТВА ГРУНТОВ М.16.1. Чем вызываются динамические воздействия на грунты? Динамические воздействия связаны с вибрацией вследствие действия машин и механизмов, особенно с неуравновешенными вращающимися частями, с ударными воздействиями, со взрывами, с перемещающимся транспортом, с сейсмическим воздействием, действием фильтрационных потоков и др. М.16.2. Как можно подразделить динамические воздействия на грунты? Динамические воздействия можно подразделить на слабые, которые могут часто действовать относительно длительное время, и сильные, которые могут действовать и кратковременно, возможно даже однократно (удар, взрыв). По времени действия усилия подразделяются на длительно действующие и кратковременные. М.16.3. Что происходит в грунтах при динамических воздействиях на них? Вибрация во время динамических воздействий уменьшает силы междучастичного трения и сопротивление сдвигу. Сильные импульсные воздействия могут вызвать дополнительные осадки и просадки. При определенной частоте колебаний междучастичное трение в сыпучих грунтах может настолько уменьшиться, что грунт приобретает свойства вязкой жидкости даже при малом количестве воды в нем. При наличии большого количества воды в грунте она может не успеть покинуть поры, в которых находилась, поэтому возникает поровое противодавление, уменьшающее сопротивление сдвигу. При динамических воздействиях в основном уменьшаются межчастичные силы трения, а в меньшей степени уменьшается угол внутреннего трения. Угол внутреннего трения будет уменьшаться вследствие разрыхления грунта, то есть увеличения его пористо- сти (рис.М.16.3). При ускорениях колебаний до одного "g", как показали опыты, угол внутреннего трения практически не изменялся. Удельное сцепление после действия динамических нагрузок также может уменьшиться, однако, как правило, незначительно, но для этого нужны достаточно интенсивные динамические воздействия, разрушающие цементационные связи. Причиной слабого уплотнения маловлажных глинистых грунтов является наличие большой связности у частиц, и, как следствие, относительно высокая прочность агрегатов частиц грунта. М.16.4. В чем заключается разжижение песчаных грунтов? 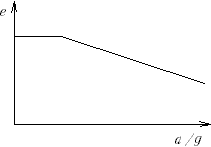 Разжижение песчаных грунтов заключается в том, что с ростом частоты колебаний они начинают "течь" как вязкая жидкость. Разжижение начинается после преодоления порога колебаний по частоте. До разжижения, при меньшей частоте колебаний до этого порога, проявляется виброползучесть. Чаще всего разжижаются водонасыщенные мелкие и пылеватые пески. Чем больше пористость грунта, тем при меньших динамических воздействиях начинается разжижение. Отсутствие в грунте напряжений именно переменного знака исключает возможность разжижения песчаных грунтов. Статическая нагрузка не только снижает возможность разрушения структуры грунта, но и уменьшает уплотняемость несвязных грунтов при динамической нагрузке. М.16.5. Что представляет собой виброуплотнение грунта? Виброуплотнение это уменьшение пористости грунта при динамическом воздействии на него. При отсутствии внешней пригрузки уплотнение сыпучих грунтов песков начинается при любых, даже слабых динамических воздействиях, и при этом может быть достигнуто почти полное их уплотнение. М.16.6. Какое воздействие на грунты оказывают взрывы в них? 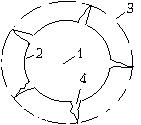 При взрыве на грунт действует высокое давление, создающее сферическую ударную волну. За фронтом этой волны происходит сжатие грунта и смещение по радиальным направлениям, а за счет этого в тангенциальном направлении происходит раздвижка грунта и получаются радиальные трещины (рис.М.16.6). М.16.7. Для каких целей применяются взрывы в строительстве? Взрывы в строительстве применяются для рыхления грунтов при их разработке, а также для их уплотнения, например при предварительном замачивании лессовидных просадочных грунтов или мелких и пылеватых рыхлых песков. Взрывы применяются в скважинах для их расширения при устройстве набивных свай и опор. Применяются также направленные взрывы для перемещения земляных масс это взрывы на выброс. Таким образом представляется возможным создавать дамбы и земляные плотины. М.16.8. Какие виды грунтов наиболее опасны при наличии сейсмических воздействий? Сейсмические колебания могут вызвать потерю устойчивости водонасыщенных несвязных грунтов и их переход в разжиженное состояние. Относительно наименее опасными являются скальные, полускальные и крупнообломочные плотные грунты. Более опасны все виды песков плотные и средней плотности маловлажные и влажные, а также глинистые грунты с малыми значениями показателя текучести и величины коэффициента пористости. Наиболее опасными являются рыхлые пески независимо от их влажности и крупности, а также глинистые грунты с большой пористостью и водонасыщенностью. М.16.9. Чем характеризуется интенсивность колебаний при сейсмических воздействиях? Интенсивность колебаний характеризуется коэффициентом сейсмичности отношением величины сейсмического ускорения к ускорению силы тяжести. Она зависит от динамичности и формы собственных колебаний сооружения. М.16.10. Какие воздействия на грунты оказывает перемещающийся транспорт? Сотрясение грунта, обусловленное движением транспорта, обычно значительно слабее сейсмических воздействий. Однако в связи с длительностью действия этих нагрузок и если они имеют большую интенсивность, то могут служить причиной развития незатухающих осадок и даже вибротекучести грунтов. Часть I. Механика грунтов
|