Механика грунтов. Ответы на вопросы. I механика грунтов
 Скачать 0.94 Mb. Скачать 0.94 Mb.
|
|
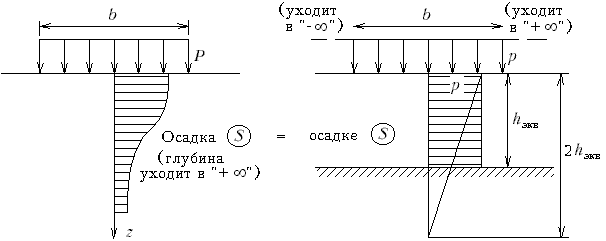
М.9.14. Когда рекомендуется применять способ расчета осадки с использованием расчетной схемы в виде линейно-деформируемого слоя конечной толщины? Этим способом предлагается пользоваться, если модуль деформации грунта основания более 100 МПа или если модуль деформации E0> 10 МПа, но ширина подошвы фундамента более 10 м. В этом случае осадочное давление считается равным полному. М.9.15. В чем состоит идея метода эквивалентного слоя (по Н.А.Цытовичу)? Идея заключается в том, что приравниваются осадки, с одной стороны, штампа (гибкого или жесткого), находящегося на упругом однородном линейно-деформируемом полупространстве, а, с другой стороны, поверхности безграничного линейно-деформируемого слоя при тех же величинах внешней нагрузки, действующей одинаково по всей границе этого слоя, и модуля деформации. В результате этого приравнивания находится толщина такого слоя hэкв, названного эквивалентным (рис.М.9.15).
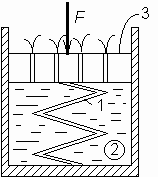
М.9.16. Для каких случаев используется в расчетной практике способ эквивалентного слоя? Для случаев неоднородных грунтов основания и при расчете затухания осадки во времени по теории фильтрационной консолидации. М.9.17. Почему в формулу осадки для жесткого штампа на упругом полупространстве не входит глубина сжимаемой толщи? Потому, что полупространство снизу не ограничено (толщина равна бесконечности) и при решении задачи отыскивается несобственный интеграл. Если бы толщина была ограничена конечным размером, она входила бы в окончательную формулу осадки. М.9.18. От каких факторов зависит коэффициент в формуле осадки для полупространства? Чему он равен для круга, квадрата, "ленты"? Этот коэффициент зависит от формы в плане загруженной площадки (квадрат, круг, прямоугольник), а также от жесткости штампа (гибкий штамп или жесткий). Для круга и жесткого штампа он равен 0,79, для квадрата 0,88, для "ленты" (соотношение размеров сторон 10:1 и более) - 2,12. М.9.19. Какой вид имеет эпюра давлений z по глубине в методе эквивалентного слоя? В методе эквивалентного слоя она имеет форму прямоугольника, распространяющегося на всю толщину эквивалентного слоя. Однако затем этот прямоугольник заменяется равновеликим треугольником с высотой, равной двум толщинам эквивалентного слоя (см. рис.М.9.15). М.9.20. Из какого предположения выводится среднее значение коэффициента относительной сжимаемости в способе эквивалентного слоя? Среднее значение коэффициента относительной сжимаемости в способе эквивалентного слоя выводится из предположения, что осадка однородного основания при среднем значении коэффициента относительной сжимаемости равна суммарной осадке отдельных слоев, то есть приравниваются осадки и, исходя из этого, получается среднее значение коэффициента относительной сжимаемости. При вычислении напряжений в пределах каждого слоя используется треугольная эпюра напряжений z по глубине, распространяющаяся на двойную толщину эквивалентного слоя (см.рис.М.9.15). М.9.21. Почему согласно способу эквивалентного слоя считается, что сжатие грунта происходит на глубину эквивалентного слоя, а не на двойную его глубину? Потому, что эпюра напряжений z считается треугольной, распространяющейся на двойную глубину эквивалентного слоя, а эта треугольная эпюра по площади равновелика прямоугольной эпюре, распространяющейся на глубину эквивалентного слоя. М.9.22*. Каким образом определяется крен жесткого фундамента? Крен рекомендуется определять, исходя из решения для эксцентрично загруженного жесткого штампа, находящегося на упругом полупространстве. Коэффициенты для формулы в зависимости от соотношения сторон вычислены и приведены, например, в СНиПе. М.10. ДЕФОРМАЦИИ ГРУНТОВЫХ ОСНОВАНИЙ ВО ВРЕМЕНИ М.10.1. С чем связано то обстоятельство, что грунты деформируются не сразу после приложения нагрузки, а на это требуется определенное время? Это связано с тем, что деформация грунта определяется изменением его пористости и для деформирования грунта нужно деформирование междучастичных связей. Эти связи часто бывают вязкопластичными и деформируются не сразу, а с течением времени. Кроме того, в порах грунта содержится вода и изменение пористости, особенно полностью водонасыщенного грунта, связано с необходимостью отжатия воды из пор грунта, на что требуется время. М.10.2. С какой скоростью в твердых телах распространяются напряжения? В твердых телах напряжения распространяются со скоростью звука. М.10.3. Какой представляется модель полностью водонасыщенного глинистого грунта? Что моделирует диаметр отверстий в поршне? К.Терцаги предложил для полностью водонасыщенного глинистого грунта такую модель: цилиндр, заполненный водой, внутри которого имеется стальная пружина. Цилиндр закрыт поршнем, имеющим весьма малые отверстия. Если на этот поршень поставить груз, то опускание поршня возможно только за счет выдавливания из цилиндра лишней воды. Поршень начнет надавливать на пружину и остановится лишь тогда, когда все усилия груза полностью передадутся на пружину. При этом лишняя вода из цилиндра выдавится наружу. Диаметр отверстий моделирует фильтрационную способность грунта чем мельче отверстия, тем медленнее выдавливается вода и медленнее идет процесс осадки (рис.М.10.3).
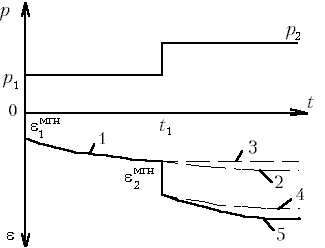
М.10.4. В чем заключаются предпосылки теории фильтрационной консолидации? Предпосылки теории фильтрационной консолидации сводятся к следующему: скелет грунта линейно-деформируемый, деформируется мгновенно после приложения к нему нагрузки и вязкими связями не обладает; структурной прочностью грунт не обладает, давление в первый момент полностью передается на воду; грунт полностью водонасыщен, вода и скелет объемно несжимаемы, вся вода в грунте гидравлически непрерывна; фильтрация подчиняется закону Дарси. М.10.5. Какие напряжения вызывают сжатие грунта? Только эффективные, то есть передающиеся на скелет грунта. Нейтральное давление на сжатие грунта не влияет. М.10.6. Какие случаи изменения полного давления (эпюры напряжений z) рассмотрены на практике и являются типовыми? Рассмотрены три случая: 1) эпюра прямоугольная; 2) эпюра треугольная с вершиной вверху, у границы (имеется в виду сжатие грунта от собственного веса); 3) эпюра треугольная с вершиной внизу и конечной ординатой вверху (эта эпюра соответствует способу эквивалентного слоя). М.10.7. Какой вид имеет основное уравнение (уравнение Павловского), из которого выводится уравнение теории фильтрационной консолидации? Каков его физический смысл? Это уравнение для одномерного случая имеет вид где q единичный расход фильтрующейся воды (скорость), м/с; n пористость грунта; z координата (вдоль оси z происходит фильтрация), м; t - время, с. Это уравнение неразрывности (сплошности). М.10.8. Какой вид имеет уравнение фильтрационной консолидации для одномерной задачи и пространственной (трехмерной) задачи? Уравнение для одномерной задачи следующее: 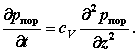 Для пространственной задачи оно имеет вид 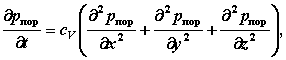 где cV коэффициент консолидации; Как видно из этих уравнений, оба они линейные относительно М.10.9. С помощью какого допущения линеаризуется уравнение фильтрационной консолидации? Уравнения, приведенные в п.М.10.8, линейные. Однако при их выводе пришлось прибегнуть к допущениям. Одно из них заключается в следующем. Уравнение фильтрационной консолидации линеаризуется с помощью того, что используется среднее значение коэффициента пористости eсред, поэтому 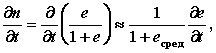 и принимается линейная зависимость между приращениями коэффициента пористости и эффективного давления (закон пористости) 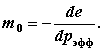 М.10.10. Что представляет собой коэффициент консолидации, на что он указывает и какую имеет размерность? Коэффициент консолидации 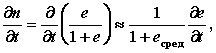 и имеет размерность м2/с. Он указывает на скорость прохождения процесса консолидации чем больше коэффициент консолидации, тем быстрее она проходит. М.10.11*. Какой порядок имеет уравнение фильтрационной консолидации и к какому типу дифференциальных уравнений оно принадлежит? Уравнение Фурье линейное, второго порядка и параболического типа. Оно является уравнением, описывающим нестационарный процесс, так как содержит время. М.10.12*. В чем состоит метод Фурье решения уравнения теории фильтрационной консолидации? Метод Фурье состоит в следующем. Поскольку основное уравнение линейное и содержит два переменных аргумента (координаты и время), то решением его будет сумма частных решений. Частные решения отыскиваются в виде произведения двух неизвестных функций одной от координаты, другой от времени. В результате мы получаем уравнение, распадающееся на два обыкновенных дифференциальных уравнения, которые легко интегрируются. Дальнейшая задача связана с определением постоянных интегрирования исходя из граничных и начального условий. М.10.13*. Какие граничные и начальное условия ставятся для слоя глинистого грунта? Начальное условие: при t = 0 имеем p=pпор, а pэфф = 0, то есть в первый момент все давление передается на воду, а на скелет не передается. Граничные условия в задаче о слое грунта, лежащем на водоупоре, сводятся к тому, что: 1) на верхней границе полное давление равно эффективному, то есть при z = 0 и t>0 имеем pэфф = p, pпор = 0; 2) на нижней границе имеем нулевой градиент, то есть при z = h имеем М.10.14*. В чем заключается некорректность в постановке граничных условий для слоя глинистого грунта? Незначительная некорректность заключается в рассмотрении начального момента времени t = 0 и верхней границы z = 0. С одной стороны, исходя из начального условия при t = 0 на верхней границе pпор = p, но в то же время на верхней границе при z = 0 должно быть pэфф = p. Поэтому приходится граничное условие рассматривать при t>0, но не при t = 0. М.10.15. Что представляет собою фактор времени и какую он имеет размерность? Фактор времени М.10.16. Что представляет собою степень консолидации, на что она указывает, в каких пределах изменяется и какова ее размерность? Степень консолидации U указывает на то, какая часть полной осадки произошла к данному моменту времени. Степень консолидации безразмерна и изменяется от нуля (при t = 0) до единицы (при t = ). М.10.17. Каким образом следует вести расчет по теории фильтрационной консолидации, чтобы воспользоваться готовыми таблицами? Следует найти, задаваясь степенью консолидации U, по таблице величину фактора времени N и далее по формуле по N найти соответствующую величину времени t. Таким образом вычисления сильно упрощаются. М.10.18. Каким образом изменяется время консолидации для двух слоев различной толщины при одной и той же степени консолидации? В этом случае отношение времен оказывается пропорциональным отношению квадратов высот (так как U одно и то же, то и N одно и то же), следовательно, если отношение высот равно 10, то время для достижения одной и той же степени консолидации будет не в 10, а в 100 раз больше. М.10.19. Каким образом ползучесть грунта влияет на осадку глинистого грунта во времени? Учет ползучести скелета грунта обычно изменяет процесс протекания осадки грунта во времени. В частности, если грунт не полностью водонасыщен, то порового давления почти не возникает. В маловодонасыщенном грунте влага при его сжатии перемещается вместе со скелетом и поровое давление практически отсутствует. Сжатие относительная деформация в слое происходит во всех точках одинаково, а скорость общей осадки прямо пропорциональна толщине слоя. Ползучесть скелета затягивает процесс деформирования. При полностью водонасыщенном грунте относительная деформация разная в различных точках по глубине слоя. Она зависит от времени и координаты точки. Ползучесть увеличивает при этом поровое давление по сравнению с тем, когда ее нет, и деформации в скелете считаются происходящими мгновенно, как в модели грунтовой массы. Осадка при проявлении ползучести будет происходить более медленно, чем без нее. М.10.20*. В чем состоит основная идея уравнения наследственной ползучести Больцмана-Вольтерры? Основная идея состоит в том, что при каждой ступени нагрузки процесс протекает независимо от того, какая нагрузка была до этого, но считается, что от всех предыдущих ступеней нагрузки процесс не завершился. Поэтому процесс как бы ступенчато сдвинут, а конечный результат, поскольку уравнение линейно, является суммой (интегралом) результатов всех предшествующих нагружений. На рис.М.10.20 представлены диаграммы, иллюстрирующие процесс деформирования, описываемый теорией наследственной ползучести.
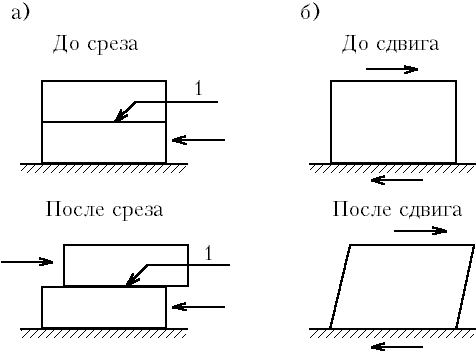
М.10.21*. Каким образом следует получить ядро ползучести и какие три случая при этом встречаются? Ядро ползучести получается экспериментальным путем. Для различных стадий ползучести оно описывается принципиально различными функциями. Три случая, это: 1) затухающая ползучесть; 2) установившаяся ползучесть и 3) прогрессирующая ползучесть. Если взять кубик связного грунта (глины), то при малых давлениях, прикладываемых к нему сверху, происходит затухание осадки со временем и ее стабилизация (фаза затухающей ползучести). При дальнейшем увеличении нагрузки осадка будет нарастать практически с постоянной скоростью и не стабилизироваться (фаза установившейся ползучести). Дальнейший рост нагрузки приведет к такому состоянию, когда скорость нарастания осадки будет со временем расти и, наконец, произойдет полное разрушение грунта. Это фаза прогрессирующего течения или прогрессирующей ползучести (см.также М.12.3). М.10.22. Чем различаются первичная и вторичная консолидация? Первичная консолидация это фильтрационная консолидация. Вторичная консолидация связана с ползучестью скелета грунта, которая при первичной консолидации не учитывается. Расчет деформаций с учетом вторичной консолидации связан со значительными математическими сложностями даже при решении одномерной задачи. М.11. ПРОЧНОСТЬ ГРУНТОВ И МЕТОДЫ ЕЕ ОПРЕДЕЛЕНИЯ М.11.1. Чем вызывается сопротивление грунта срезу? Сопротивление грунта срезу вызывается сопротивлением междучастичных связей, зависящим от прикладываемого давления. Прочность связей зависит от вида грунта, его влажности и плотности. М.11.2. Какая разница между срезом и сдвигом? Какой вид имеет схема прямого среза? Срез происходит по определенной поверхности. Схема разрушения представлена на рис.М.11.2. Деформация сдвига захватывает некоторый объем и связана с перекашиванием прямоугольного элемента. Под прямым срезом в механике грунтов понимается срез, изображенный на рис.М.11.2, однако часто под сдвигом понимается и прямой срез, а эти понятия отождествляются.
|