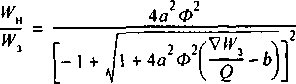Теплофикация и тепловые сети. И тепловые

• Название: И тепловые
• Анкор: Теплофикация и тепловые сети
• Дата: 27.03.2022
• Размер: 2.4 Mb.
• Имя файла: Теплофикация и тепловые сети.docx
• Тип: Учебник; #420164
• страница: 21 из 101

Рис. 4.1. Зависимость Q

1 — качественное регулирование, 2 — качественно- количественное регулирование, 3, 4 — количествен­

ное регулирование

При количественном регулировании т > 1. Тогда как видно из уравнения (4.5)

Q>W.

При качественно-количественном регу­лировании 0 < т < 1. Как видно из выражения (4.5), в этом случае

Q

На рис. 4.1 приведена зависимость

Q при различных системах регу­лирования.

3. 
   ТЕПЛОВЫЕ ХАРАКТЕРИСТИКИ ТЕПЛООБМЕННЫХ АППАРАТОВ И УСТАНОВОК
   

Оборудование абонентских установок состоит из различного рода теплообменных аппаратов, нагревательных приборов, водо­водяных подогревателей, калориферов и т.п.

Расчет регулирования современных сис­тем централизованного теплоснабжения проводится по уравнениям, описывающим работу различного типа теплообменных ап­паратов в нерасчетных условиях. В таких условиях обычно известны только темпера­туры теплоносителей на входе в теплоис­

пользующие установки и, как правило, неизвестны температуры теплоносителей на выходе из них. Поэтому уравнение теп­ловой нагрузки теплообменных аппаратов в форме Q = АТА/ неудобно для расчета ре­жимов регулирования, так как заранее неиз­вестно значение А/, которое в этом случае приходится определять методом последова­тельных приближений.

Расчет регулирования значительно об­легчается при использовании так называе­мых тепловых характеристик теплообмен­ных аппаратов, в которые в качестве мно­жителя входит не средняя разность темпе­ратур между теплообменивающимися пото­ками А/, а максимальная разность темпера­тур греющей и нагреваемой сред на входе в аппарат Д, которая при расчете регулиро­вания, как правило, известна.

Тепловая нагрузка всех видов конвек­тивных теплообменных аппаратов может быть определена по уравнению характери­стики [60, 101, 106]

2-eW^V, (4.6)

где Е — удельная тепловая нагрузка на еди­ницу меньшего эквивалента расхода И^/_м и на 1 °C максимальной разности температур V, или коэффициент эффективности теплообменного аппарата; 1Т_М = (Gc)_M — меньшее значение эквивалента расхода те- плообменивающихся сред, Дж/(с'К) или ккал /(ч ■ °C); G — расход теплоносителя, кг/с или кг/ч; с — теплоемкость теплоно­сителя, Дж/(кг'К) или ккал/(кг-°C); V = = Tj - /₂ — максимальная разность темпе­ратур между греющим и нагреваемым теп­лоносителями, т.е. разность температур греющего и нагреваемого теплоносителей на входе в аппарат, °C; Т] — температура греющего теплоносителя; /₂ — температу­ра нагреваемого теплоносителя; индекс 1 соответствует «горячему концу» теплоно­сителя, т.е. греющему на входе в аппарат и нагреваемому на выходе из него; индекс 2 — «холодному концу» теплоносителя, т.е.

греющему на выходе из аппарата и нагре­ваемому на входе в него.

Величина е представляет собой тепло­вую нагрузку аппарата, отнесенную к еди­нице меньшего эквивалента расхода тепло- обменивающихся потоков и I °C макси­мальной разности температур.

Если при выводе уравнения характери­стики теплообменных аппаратов принима­ется среднелогарифмическая разность тем­ператур между греющей и нагреваемой сре­дами, то выражение для расчета коэффици­ента эффективности е принимает вид экспо­ненциальной зависимости.

При использовании наиболее простых схем теплообменных аппаратов, когда движение теп- лообменивающихся сред происходит по принци­пу противотока или прямотока, эти имеют следующий вид [46, 60, 106]:

противоточный аппарат

_{е =} . J--g

'-V

прямоточный аппарат

- 0)(^_м/^+ 1)

где ш = kF/ W_M — режимный коэффициент; kF — произведение коэффициента теплопередачи теп­лообменного аппарата на площадь его поверхно­сти нагрева; W_M, W₅ — меньшее и большее зна­чения эквивалентов расхода теплообмениваю- шихся сред; е = 2,718 — основание натуральных логарифмов.

Для аппаратов с перекрестным током тепло­носителей уравнения для расчета коэффициента е представляют собой очень сложные зависимо­сти, практически непригодные для обычных ин­женерных расчетов. Для некоторых случаев пе­рекрестного тока (например, с самоперемеши- ваюшимися теплоносителями) в литературе во­обще отсутствуют уравнения для расчета коэф­фициента Е.

Уравнение для расчета коэффициента е значительно упрощается, если при его выво-



де разность температур между греющей и нагреваемой средой описывается линейной зависимостью, имеющей в пределах исполь­зования уравнения характеристики близкую сходимость со среднелогарифмической раз­ностью температур. В качестве такой линей- 122
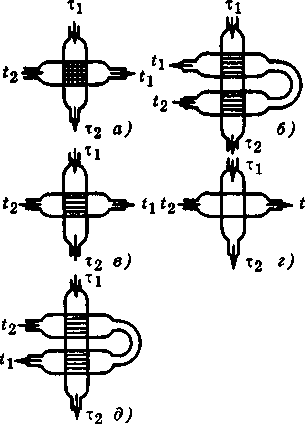
Рис. 4.3. Схемы движения теплоносителя при
перекрестном токе

а — оба теплоносителя без перемешивания; б — два
хода одного теплоносителя без перемешивания проти-
вотоком и одни ход другого теплоносителя с переме-
шиванием; в — один ход одного теплоносителя без
перемешивания и один ход другого теплоносителя с
перемешиванием; г — оба теплоносителя с переме-

шиванием; д — два хода одного теплоносителя без
перемешивания прямотоком и один ход другого теп-
лоносителя с перемешиванием

ной зависимости и при всех практически применяющихся схемах движения теплоно­сителей в теплообменных аппаратах (рис. 4.2 и 4.3) может быть использована за­висимость, предложенная автором [101, 106];

Д? = V - aSt_M - b8t₆, (4.8)

где Д/— средняя разность температур меж­ду греющей и нагреваемой средами, °C; St— перепад температур теплоносителя в теплообменном аппарате, °C; для греющего теплоносителя 5/ = Tj — т₂, для нагреваемо­го 8Z = f _t - t₂i индекс «б» соответствует боль­

шему перепаду температур теплоносителя, индекс «м» — меньшему; а и Ь — постоян­ные коэффициенты, зависящие от схемы движения теплоносителя в теплообменнике.

На рис. 4.2 и 4.3 показаны различные схемы движения теплоносителей. При всех схемах значение коэффициента Ь в (4.8) по­стоянно и равно 0,65. Ниже приведены зна­чения коэффициента а для рассматривае­мых схем движения теплоносителей:

ТЕПЛОФИКАЦИЯ И ТЕПЛОВЫЕ СЕТИ 1

ЭНЕРГЕТИЧЕСКАЯ ЭФФЕКТИВНОСТЬ ТЕПЛОФИКАЦИИ 22

31 35

ТЕПЛОВОЕ ПОТРЕБЛЕНИЕ 66

«V' ^_ ^с(^В р ^— ^11 о)’ 74

'1’н1 93

СИСТЕМЫ ТЕПЛОСНАБЖЕНИЯ 100

.Es 113

РЕЖИМЫ РЕГУЛИРОВАНИЯ СИСТЕМ ЦЕНТРАЛИЗОВАННОГО ТЕПЛОСНАБЖЕНИЯ 148

8,=8-8₂. (4.68) 194

Й>1 = W'/W'_o= ; 206

О^р О 208

iV, = W₀₊iV_r = ₊ (4.85а) 208

*2 = W'_Q-^_r 208

Qo ' 212

а_т=е'_отМ- (4.IH) 219

а и Ь. 222

ГИДРАВЛИЧЕСКИЙ РАСЧЕТ ТЕПЛОВЫХ СЕТЕЙ 231

8jPi.2 8/?1, 263

ГИДРАВЛИЧЕСКИЙ РЕЖИМ ТЕПЛОВЫХ СЕТЕЙ 275

ⁿ\^Q ^{+ s}c 278

■Н_п 278

Н, 278

У m = — • (6.20) 286

V ^{1 S}B-n ^sC-n ^SM-n ^Sm 286

= 7/yPg называется давлением гидравли­ческого удара. 306

z_y = lla, (6.58) 308

/⁼ 1\.2 ⁺h.-l ⁺ /з-4 ⁺ ^5-6 ^{+ 1}в-\- 308

H_y = Jllg, 309

р_у<(р_л-р_р). (6.62) 309

где s_B = ар / f— волновое сопротивление 309

Волновое сопротивление равно давле­нию (напору) гидравлического удара, возни­кающему в трубопроводе при изменении 309

в нем объемного расхода на 1 м /с за время 310

Н = Н /7Л 310

Н - Н у‘°/у‘ 310

ТЕПЛОФИКАЦИОННОЕ ОБОРУДОВАНИЕ ТЭЦ 313

1/а, + 1/а₂ + S5/X 318

ОБОРУДОВАНИЕ ТЕПЛОВЫХ ПУНКТОВ (ПОДСТАНЦИЙ) 328

Н„ = Н_о - AZ = Н_о- (Z_c - Z_a) = idem, (8.1) 331

Н_О = Н_П + AZ. (8.2) 331

d₃ 2g 342

— = ^с— ; и = GJG_n— коэффицн- 346

0,6и+ 2-7о,36и²+2,4и+2,4 348

чЛ'в-‘_н№ = 2₀^d-+ > или 364

n ^FSP^CP 364

. Q_o ^

t,Q_o^_oy _/о_ 365

д₀У _е^2/Р 365

Q_o 365

О2₀^/(1₀Г) 365

ОБОРУДОВАНИЕ ТЕПЛОВЫХ СЕТЕЙ 378

^d_B 404

п₂ = = Pdj/W = pd_B/(2$), (9.7) 404

M₀ = q/²/12, (9.12) 405

Я = и ⁺ Я²_г> (9 13) 405

/ = jYla^W/q (9 17а) 406

NR> Q_Bs + Q_Bp.r, (9.19) 409

S = nd²_abpap. (9.24) 412

п. — . \⁷ '^а) 417

\EJ 418

к 418

„ г у² ds 418

к к 418

^Edm_maxy 418

+ 0,67/³ + /,/² - 4/?/² + 2/?²/- 1,33/?³} 419

ст= 1,5ДЕб/(л+I)//² (9 51) 420

i_K = 4>r/l, (9.53) 420

ТЕПЛОВОЙ РАСЧЕТ 423

т -1₀= qR\ (10.2) 423

R = Л_в + Я_тр + Л_и + R_H, (10.4) 423

Д=1/(я<Ах), (10.5) 424

AR 428

, (10.18) 428

₌ ln(4t/J) ₍₁о.2о) 430

h„ = h + h^, (10.21) 430

^R4K ^{+ R}K ^{+ Л}гр 431

!//?,+ ! /R₂+...+1 /R_n+ 1 /Л_к._о 431

R_o = —±—\nJTT(2h/b')², (10.30) 2лХп, 432

1х² + (у + /г)² 432

Q_M = ql₃, (10.36) 432

T}_H = (Q_r-Q_H)/Q_r=i-Q»/Qr (Ю.38) 433

А₂ = А,-g/(l+g)/G (10.41) 433

R = R_CU+R = In — 436

Контрольные вопросы и зодания 437

ЭКСПЛУАТАЦИЯ ТЕПЛОВЫХ СЕТЕЙ 438

^С 'к 444

(E_H+f)k_H (11.5) 445

t - t В II 449

^{_ _}Q р 449

b + cl 449

относительная повреждаемость теп­ловой сети 452

относительный аварийный недоотпуск тепловой энергии 452

Qo ⁷ 455

⁷Qo ⁷ 455

Qo 455

pg 461

z = -2 2 ₊ 462

МЕТОДЫ РАСЧЕТА ЭФФЕКТИВНОСТИ ИНВЕСТИЦИЙ В ЭНЕРГЕТИЧЕСКИЕ ОБЪЕКТЫ 470

Р ⁼ Рср ^{+ ь + с}> О²-⁹) 480

^ок " чдд₅ - чдд₄ ' 482

ТП- О'. т К. 482

т П. - О' 482

₊ ЧДД,(р₂-Р|) ^{Pl +} чдд, -чдд₂ 483

I 0,(1 + Р)‘ 483

_Ид ₌ = 484

ВР\ - И_{ - //, = ВР₂ - И₂ - Н₂. (12.21) 488

Р = П_щк,/К, (12.24) 488

РАСЧЕТ ТЕХНИКО-ЭКОНОМИЧЕСКИХ ПОКАЗАТЕЛЕЙ ТЕПЛОСНАБЖАЮЩИХ СИСТЕМ 490

+1)]а, (13.3) 491

^G_{В п} ГП Л_д 494

^L = i^L^i^^G- <¹³-¹²) 494

К_йК = к_йКУ, (13.15) 495

А-_аб = Л_рЛ (13.17) 495

К,_я = К_тб + К_тт, (13.19) 495

Затраты на сырье и основные материа­лы, руб/год, определяются в виде 497

И = У У^к Ц* + 497

Затраты на вспомогательные мате­риалы, руб/год, покупаемые со стороны, 497

т 497

Затраты на топливо определя­ 497

пдв 501

а) Земельный налог 503

г) Налог на владельцев транспортных средств 505

G.^p,n_l G₂^P2^2 507

Др_с = Л_л£(1 + а), (13.62) 507

т 1 + т₂ + ... + т_п 509

3 = + М_{у с} <7_{Т с}т_? + (/, + £) х 521

■k^>(E+ftk_mly. (13,98) 523

у_р = m(b + cf)d^1,2, (13.103) 524

^Т" ^Тн - ¹ 525

ОГЛАВЛЕНИЕ 571

Если в (4.8) под Д? понимается средне­арифметическая разность температур (как это обычно имеет место при расчете по­верхностей нагрева радиаторов отопитель­ных установок), то а = 0,5 и Ь = 0,5.

При использовании предложенной авто­ром линейной зависимости (4.8) для сред­ней разности температур уравнение для расчета коэффициента эффективности име­ет вид [101] где со = kF/ — режимный коэффициент; е» — коэффициент эффективности теплооб­менного аппарата с бесконечно большой поверхностью нагрева (F —>• оо).

Значение е* находится на основе экспо­ненциальных уравнений расчета е для про- тивоточных и прямоточных аппаратов на основе формул (4.7) из условия F = оо.

Введение знака неравенства в правую часть (4.9) связано с использованием при выводе расчетного уравнения для е линей­ной разности температур (4.8) вместо сред­нелогарифмической.

Неравенство указывает на то, что физи­чески значение е не может превысить значе­ние так как температура нагреваемой среды ни в одном из сечений теплообменно­го аппарата не может превысить температу­ру греющей среды, поскольку локальные значения разности температур теплообме- нивающихся сред всегда больше нуля, т - -Г>0.

Для соблюдения неравенства в правой части (4.9) пользуются следующим прави­лом: если при расчете по (4.9) получается е < е», то это значение е и принимается для дальнейших расчетов; в том случае, если е > е», для дальнейших расчетов принима­ется е = е».

При противотоке, а также в тех случаях, когда в процессе теплообмена изменяется фазовое состояние одного или обоих тепло­носителей (конденсация, кипение), е* = 1;

при прямотоке е. =

Уравнение (4.9) действительно во всей области возможного практического исполь­зования теплообменных аппаратов, т.е. в пределах 0 < WJ £ 1; 0 £ ш £ °о. Другой области физически не существует.

Уравнения (4.6)—(4.9) универсальные. Они действительны при любой схеме дви­жения теплоносителей. На основе этих уравнений может быть практически решена любая задача, связанная с режимом работы теплообменных аппаратов в нерасчетных условиях.

Поскольку для противоточных аппара­тов при F = оо е = 1, то из (4.6) следует, что коэффициент эффективности противоточ- ного теплообменника представляет собой отношение тепловой нагрузки данного теп­лообменника к тепловой нагрузке теплооб­менника с бесконечно большой площадью поверхности нагрева при одинаковых в обо­их случаях значениях меньшего эквивален­та расхода теплообменивающихся потоков и при одной и той же максимальной разно­сти температур.

Когда в процессе теплообмена имеет ме­сто изменение фазового состояния одного из теплоносителей (пароводяные подогре­

ватели, паровоздушные калориферы, испа­рители с водяным обогревом и др.), т.е. ко­гда IVq = оо, уравнение (4.9) принимает вид

Если в процессе теплообмена меняется фазовое состояние обоих теплоносителей, т.е. когда W₆ = fF_M = оо, уравнение характе­ристики (4.6) принимает вид

Q = kFV. (4.1!)

Сопоставление результатов расчета по (4.9) с результатами расчета по экспонен­циальным уравнениям, базирующимся на среднелогарифмической разности темпера­тур, показывает хорошую сходимость. Максимальное расхождение для аппара­тов, в которых имеет место изменение фа­зового состояния одного из теплоносите­лей, составляет около 6 %. Для аппаратов, в которых фазовое состояние теплоносите­лей не меняется, в частности для противо- точных водо-водяных подогревателей, максимальное расхождение обычно не пре­вышает 3—4 % [106].

Из совместного решения уравнений теп­лопередачи и теплового баланса выводится также предложенное автором уравнение для расчета коэффициента эффективности отопительных установок с учетом режима работы смесительного узла присоединения к тепловой сети [101]

0,5 + и 1 " * ’

— + —

1 + и со

где и — коэффициент смешения в узле при­соединения; со - k₀F/ 1V₀ — режимный коэф­фициент; k₀F— произведение коэффициен­та теплопередачи нагревательных приборов установки на площадь их поверхности нагрева²¹; W_o — эквивалент расхода сетевой воды, поступающей в узел присоединения отопительной установки.

При выводе (4.12) принято 1К_М/ ИС = 0 в связи с тем, что эквивалент расхода возду­ха, омывающего отопительные приборы, IV₆ во много раз больше эквивалента расхо­да греющей воды протекающей через нагревательные приборы отопительной ус­тановки. Кроме того, в исходном уравнении теплопередачи отопительных приборов принята среднеарифметическая разность температур, поскольку к этой разности тем­ператур относятся обычно все эксперимен­тальные и расчетные значения коэффици­ентов теплопередачи нагревательных при­боров отопительных установок.

В частном случае, при отсутствии сме­сительного устройства в узле присоедине­ния отопительной установки, т.е. при и = О, уравнение (4.12) принимает вид

Поскольку при F = оо е₀ = 1, то из (4.6) следует, что коэффициент эффективности отопительной установки представляет со­бой отношение тепловой нагрузки данной отопительной установки к тепловой нагруз­ке отопительной установки с бесконечно большой площадью поверхности нагрева­тельных приборов при одинаковых в обоих случаях расходах и температурах сетевой воды, поступающей в отопительную уста­новку и одинаковых внутренних температу­рах отапливаемых помещений.

Коэффициент теплопередачи теплооб­менных аппаратов к является переменной величиной, зависящей от условий теплооб­мена. В аппаратах с принудительной кон­векцией (водо-водяные и пароводяные по­догреватели, паро- и водовоздушные кало­

риферы и др.) коэффициент теплопередачи зависит в первую очередь от скорости теп­лоносителей, не изменяющих своего агре­гатного состояния в процессе теплообмена.

Для упрощения расчета режимов регу­лирования значение режимного коэффици­ента аппарата (0 можно определять точно расчетным или опытным путем только для одного произвольно выбранного режима работы аппарата, который назовем основ­ным. Будем обозначать этот режим индек­сом «ос». При всех других режимах работы этого аппарата его режимный коэффициент можно определить путем пересчета по предложенной автором формуле

со = aJrn'ir”²/W_M, (4.14)

где и_ос = k_QZFI(W_MQi:) — режимный коэф­фициент для основного режима; к_ос — ко­эффициент теплопередачи подогревателя при основном режиме; W_n = ^_п/^_пос!

^ = ^_в/^_в._ос; = ^_M/Pr_MOC; FK_noc,

W^Z_{B ос}, W_{M ос} — эквиваленты расхода тепло­носителей соответственно первичного (греющего), вторичного (нагреваемого) и меньшего из них при режиме аппарата, при­нятом за основной; W_n, И^/_в, IV_M — эквива­ленты расхода этих же теплоносителей при любом режиме работы аппарата.

В зависимости от режима может иметь место как W_n = 1Т_М, так и W_B = W_M.

Показатели степени и т₂ зависят от вида теплоносителя, конструкции подог­ревателя и состояния поверхности нагре­ва. В противоточных секционных водо-во­дяных подогревателях = 0,33—0,5; «2 — 0,33—0,5. Как показывают результа­ты испытания, при расчете водо-водяных подогревателей можно практически при­нимать И] = т₂ = 0,5, тогда (4.14) принима­ет вид

щ = Ф^₆/^_ы, (4.15)

где Ф — параметр водо-водяного подогре­вателя, для данного подогревателя величи­на практически постоянная,

^ф = (4.16)

Как показали проведенные исследова­ния, значение параметра секционных водо­водяных подогревателей прямо пропорцио­нально их длине:

Ф=Ф_у/, (4.17)

где Фу — удельный параметр, отнесенный к единице длины подогревателя; / — длина подогревателя, м.

Удельный параметр Ф_у зависит в основ­ном от отношения площадей сечений труб­ного и межтрубного пространств и практи­чески не зависит от удельной площади по­верхности нагрева, приходящейся на еди­ницу длины подогревателя, т.е. от номера или диаметра корпуса подогревателя. Пара­метр подогревателя остается практически постоянным в широком диапазоне измене­ния W₅ и W_M [39, 101].

Для всех типоразмеров секционных водо-водяных подогревателей, приведен­ных в приложении 20, можно практически принимать одно и то же значение удельного параметра Ф_у = 0,11/м при чистой поверх­ности нагрева, т.е. при отсутствии на ней накипи и загрязнений.

Можно также принимать для всех типо­размеров пластинчатых подогревателей, приведенных в приложении 21, практиче­ски одно и то же значение удельного пара­метра одного канала Ф_у = 1,1/м.

Для пароводяных подогревателей и паро­воздушных калориферов, в которых имеет место конденсация греющего пара, при тур­булентном течении нагреваемой среды мож­но принимать в (4.14) = 0, т₂ 0,33—0,5.

Для водовоздушных калориферов при турбулентном течении теплоносите­лей можно принимать Щ] = 0,12—0,20 и т₂ = 0,33—0,5.

Из совместного решения (4.9) и (4.15) выводится предложенная автором формула для расчета коэффициента эффективности противоточных водо-водяных подогре­вателей

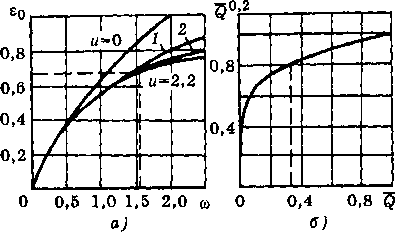
Зависимость е = /(Ф, приведена на

рис. 4.4. Зная эквиваленты и Wg, пара­метр подогревателя Ф и температуры грею­щей и нагреваемой сред т, и t₂ на входе в теплообменный аппарат, легко с помо­щью рис. 4.4 или (4.18) определить значе­ние е, а затем по (4.6) — тепловую нагрузку аппарата при любом режиме.

Рассмотрим некоторые задачи из области те­плоснабжения, решаемые однозначно на основе уравнения характеристики теплообменных ап­паратов.

К этому классу задач относятся следующие:

1. 
   Определение тепловой производитель­ности теплообмеиного аппарата (нагрузки) Q при данных эквивалентах расхода теплоносите­лей W_M и 1T₆, максимальной разности темпера­тур V и параметре подогревателя Ф. Вначале на­ходят е по (4.9) или (4.18), а затем Q по (4.6).
   
2. 
   Определение максимальной разности тем­ператур V при заданных эквивалентах 1T_M и тепловой нагрузке Q и параметре подогревателя Ф. Находяте по (4.9) или (4.18), азатем V по (4.6).
   
3. 
   Определение комплекса kF или параметра подогревателя Ф при заданных эквивалентах 1Т_М и (Tg. тепловой нагрузке Q. максимальной разно­сти температур V и противоточной схеме движе­ния теплоносителей.
   

Как видно из рис. 4.2, Az₆ = V - 8z_M; Az_M = V - Sfg.

Из уравнения теплового баланса

g = 1К_б 8z_M = 1К_М 8z₆, (4.19)

откуда 8z_M = Ql W₆\ 8z₆ = Ql W_M.

Из уравнения теплопередачи

Из совместного решения следует

V- Q/HF

In

v-g/ис

kF = О —

По найденному значению kF с помощью (4.16) находят параметр теплообменного аппарата.

Аналогично может быть решена задача для прямоточной схемы.

4. 
   В некоторых задачах приходится опреде­лять неизвестное значение эквивалента расхода одного из теплоносителей по заданным зна­чениям: эквивалента расхода другого теплоноси­теля W₃, максимальной разности температур V, тепловой нагрузки Q, параметра подогревателя Ф. В частности, такая задача возникает при рас­чете режима регулирования водо-водяных по­догревателей горячего водоснабжения, когда по заданному расходу вторичного (нагреваемого) теплоносителя W₃ = необходимо найти неиз­вестный расход первичного (греющего) теплоно­сителя W_n =
   

Сложность решения такой задачи в том, что заранее неизвестно, что больше, или W_H, и по­этому нельзя непосредственно воспользоваться уравнением (4.18).

Такого типа задачи могут быть решены сле­дующим образом.

Определяют тепловую нагрузку аппарата Q, из условия равенства эквивалентов расхода греющей и нагреваемой сред, т.е. при W_H = (Т₃

Если заданное значение Q < Q*, то при заданных условиях 1Е_Н < W₃; если Q > Q„ то W_H > W₃; при Q = Q* W_H= W₃.

С помощью (4.6) и (4.18) выводят уравнение для расчета Q* секционных водо-водяных подог­ревателей: на основе (4.18) при W_M = 1К₆;

1_ ₌ Ф

^£ 1 + Ф 1 + Ф

e- = ^V^ = Y- (4.22)

Когда Q > Q*, что соответствует 1Е_Н > И'₃, зна­чение 1К_Н находят по формуле



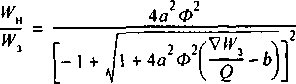
Когда Q < Q₃, что соответствует W_H < W₃, зна­чение 1Е_И находят по формуле

Тепловую нагрузку отопительных уста­новок при любом режиме работы определя­ют по (4.6) и (4.12).

Режимный коэффициент радиаторных отопительных установок определяется по формуле

—и/(1 +и)

Фдво

СО = , (4.25)

где Ф_о — параметр отопительной установки;

во - £?₀/(?_{о ос}—отношение расхода теп­лоты на отопление при данном режиме к рас­ходу теплоты на отопление при основном ре­жиме. Обычно в качестве основного режима для отопления принимают режим при рас­четной наружной температуре / В этом случае 0_О = Q_o/Q'_o; = IV_O/W'_O —

отношение эквивалента расхода сетевой во­ды на отопление при данном режиме к экви­валенту расхода сетевой воды на отопление при расчетном режиме, т.е. при наружной температуре f_{H 0}.

Параметр отопительной установки опре­деляется по формуле где 8т'_о и Д/_о — перепад температур сете­вой воды в отопительной установке и сред­няя разность температур в отопительном приборе между греющей водой и воздухом в отапливаемом помещении при расчетном режиме, т.е. при наружной температуре ?_{н 0}.

В большинстве случаев в системах цен­трализованного теплоснабжения жилых и общественных зданий

8т' = 150-70 = 80 °C;

ДГ₀ = (95 + 70)/2 - 18 = 64,5 °C;

Ф_о = 80/64,5= 1,24; и = 2,2.

В зависимости от типа отопительных приборов и схемы их присоединения к стоякам отопительной установки значе­ние показателя степени в формуле (4.25) п- 0,17—0,33. В большинстве случаев п = 0,25, в этих условиях (4.25) принимает вид