Теплофикация и тепловые сети. И тепловые

• Название: И тепловые
• Анкор: Теплофикация и тепловые сети
• Дата: 27.03.2022
• Размер: 2.4 Mb.
• Имя файла: Теплофикация и тепловые сети.docx
• Тип: Учебник; #420164
• страница: 53 из 101

Рис- 8.16. Режим работы элеватора с регулируемым

соплом на отопительную установку и, И_р, Г_с = /1/_р1)

хода воды через сопло при регулировании к расходу при отсутствии регулирования, т.е. при полном выводе регулирующей иглы из сопла; Р_с —относительный расход воды через отопительную установку — отноше­ние расхода воды через отопительную уста­новку при регулировании к расходу воды при отсутствии регулирования.

Зависимость построена по (8.41). Уста­новка регулирующей иглы вызывает сниже­ние коэффициентов скорости сопла и вход­ного участка камеры смешения [39].

В пределах изменения f _р1 от 1 до 0,2 коэффициент скорости сопла изменяется по зависимости

Ф, ⁼ 0,7 + 0,2/_р1,

Коэффициент скорости входного участ­ка камеры смешения в элеваторе с регули­руемым соплом можно принимать <р₄ = 0,9.

Кавитационный режим струйных на­сосов. Уравнение характеристики элевато­ра (8.33) и уравнение характеристики сопла (8.38) выведены при условии работы струй­ного насоса на однофазной несжимаемой жидкости.

В системах централизованного тепло­снабжения при работе струйных насосов (элеваторов) на сильно нагретой воде дав­ления на отдельных участках проточной части аппарата могут оказаться ниже давле­ния насыщенного пара при температуре протекающей воды. Такие режимы возника­ют в первую очередь на участках с наиболее высокой температурой и наиболее низким давлением теплоносителя. Такими кавита­ционными участками в струйных насосах являются выходной участок сопла и вход­ной участок камеры смешения.

Кавитация в струйных насосах сопровож­дается режимами так называемого предель­ного расхода среды, для которых характерно, что снижение давления среды за кавитацион­ным сечением не сопровождается увеличе­нием расхода. Это свидетельствует о том, что внешние возмущения, возникающие в потоке после кавитационного сечения, не пе­редаются через это сечение. Поэтому при расчете кавитационных режимов принимают обычно скорость паровой фазы в кавитаци­онном сечении равной местной скорости звука.

Кавитационный режим сопла. На рис. 8.17 показана зависимость давления р_н в приемной камере струйного насоса от рас­хода воды через сопло G_p. Давление перед соплом постоянно (р_р = const).

При отсутствии кавитации давление в выходном сечении сопла равно давлению в приемной камере. В таком режиме умень­шение давления р_н в приемной камере струйного насоса сопровождается увеличе-



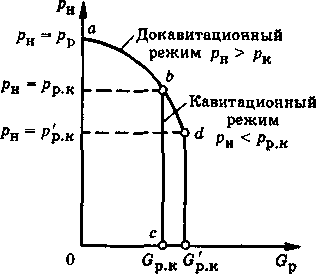
Рис. 8.17. Зависимость расхода воды через сопло от давления в приемной камере струйного насоса

нием расхода воды через сопло. Эта зависи­мость описывается уравнением

Gp = (8-42)

где Г_р — удельный объем воды перед со­плом, м³/кг.

Графически эта зависимость изображена на рис. 8.17 квадратичной параболой abd.

Если при температуре рабочей воды /_р и некотором давлении в приемной камере Рн Рр к ^в выходном сечении сопла возни­кает кавитационный режим, то при даль­нейшем снижении давления в приемной камере, т.е. при р_н < р_{р к}, давление в выход­ном сечении сопла не изменится и останет­ся постоянным р_{р к} = const; постоянным ос­танется также расход воды через сопло G_{p к} = const. Этот режим показан на рис. 8.17 вертикальной прямой Ьс. При дру­гой, более низкой температуре рабочей во­ды перед соплом t'_p < t_p кавитационный ре­жим наступит при более низком давлении в приемной камерер_н = р_рк <р_{р к}. Предель­ный расход воды через сопло в этом режиме будет более высоким G_{p к} > G_{p к}.

Проведенные исследования показыва­ют, что кавитационное давление р_{р к} в вы­ходном сечении сопла может быть опреде­лено по эмпирической формуле [68] гдер_{р н} — давление насыщенного пара при температуре воды перед соплом г_р; а — опытный коэффициент, зависящий от фор­мы и длины сопла. С увеличением длины сопла коэффициент а возрастает. Для предварительных расчетов можно принять а = 0,3—0,4.

Неравенство в правой части (8.43) пока­зывает, что кавитационное давление в вы­ходном сечении сопла р_{р к} не может быть меньше давления в приемной камере р_н. По­этому, если по (8.43) получается р_{р к} < р_н, следует принять р_{р к} = р_н. Кавитация в сопле может иметь место только прир_{р к} >р_н. Ско­рость истечения паровой фазы из сопла, м/с, при кавитационном режиме

= JbP_pK^ (8-⁴4)

где р_{р к} — давление в выходном сечении со­пла при кавитационном режиме, Па; Г_п — удельный объем сухого насыщенного пара при давлении р_{р к}, м³/кг; к — показатель адиабаты перегретого пара (для водяного пара к = 1,3).

Использование в (8.44) показателя адиа­баты перегретого, а не сухого насыщенного пара объясняется тем, что при обычном адиабатном расширении пара в сопле со­стояние сухого насыщенного пара в крити­ческом сечении сопла может быть получено только в том случае, когда перед соплом пар находился в перегретом состоянии. По­скольку в данном случае используются те же расчетные зависимости для определе­ния критической скорости, то показатель адиабаты должен относиться к состоянию пара на участке его докритического расши­рения, т.е. к перегретому пару.

Скорость водяной фазы в выходном се­чении сопла, м/с,

= Ъ&Р_р-Р_р,^_В’ (8-45) где (Pj — коэффициент скорости для водя­ной фазы. При кавитационном режиме ф! =0,97—0,99; Г_в — удельный объем воды при температуре t_{p к}, соответствующей дав­лению насыщения водяного парар_рк, м³/кг.

Энергетический баланс потока на участ­ке сопла между его входным и выходным

сечениями может быть записан в виде уравнения

2000 2000

энтальпии воды перед со­плом, пара и воды в выходном сечении со­пла, кДж/кг; х — паросодержание потока в выходном сечении сопла.

2

Величина w _в / 2000 очень мала по срав­нению с остальными членами уравнения, поэтому для упрощения ею можно пренеб­речь. Из (8.46) можно определить паросо­держание в выходном сечении сопла

А - А_ Е 2

А - А +

^{п в} 2000

Площадь выходного сечения сопла мож­но в первом приближении представить как сумму двух слагаемых — площади, зани­маемой водяным потоком, и площади, зани­маемой паровым потоком:

2

откуда массовая скорость, кг/(м • с), рабо­чего потока в выходном сечении сопла при кавитационном режиме

При отсутствии кавитации х = 0, q = w_B/i>_B.

Расход рабочего потока

С_р = <7/_р1. (8.48а)

Кавитационный режим камеры сме­шения. При постоянном перепаде давлений рабочего потока Др_р уменьшение сопротив­ления местной отопительной установки s_c приводит к увеличению развиваемого коэф­фициента инжекции и. Такая закономер-

ность действительна до тех пор, пока в ка­мере смешения элеватора не возникает кавитация.

При неизменных геометрических разме­рах элеватора и постоянных давлениях ра­бочей и инжектируемой среды р_р и р_н уве­личение коэффициента инжекции (смеше­ния) сопровождается уменьшением давле­ния р₂ во входном сечении камеры смеше­ния элеватора. Когда давление во входном сечении камеры смешения р₂ делается рав­ным давлению насыщенного пара р_{с н} при температуре /_с смешанного потока, возни­кает кавитация.

На рис. 8.18 представлена совместная характеристика элеватора и отопительной установки. На участке ab элеватор работает в докавитационном режиме. При уменьше­нии сопротивления местной системы от .?] до s₂ коэффициент инжекции увеличивает­ся от и до и_к.

При сопротивлении отопительной сис­темы s₂ возникает кавитация в камере сме­шения. При дальнейшем уменьшении со­противления местной системы, например, до Sj коэффициент инжекции остается по­стоянным: и_к = const.

Условие возникновения кавитационного режима в камере смешения р₂ ⁼Pc.h-

Метод расчета и_к приведен в [103].

6. 
   АККУМУЛЯТОРЫ ТЕПЛОТЫ
   

Для снижения начальных затрат на со­оружение системы теплоснабжения и упро­щения эксплуатации применяют различные методы выравнивания резкопеременной те­пловой нагрузки абонентов путем аккуму­лирования теплоты. При этом используется как естественная аккумулирующая способ­ность зданий и отдельных элементов систе­мы теплоснабжения (строительные конст­рукции отапливаемых зданий, трубопрово­ды тепловых сетей), так и специальные теп­ловые аккумуляторы, устанавливаемые у абонентов или в отдельных узлах системы теплоснабжения.

Аккумуляторы горячей воды. Расчет­ную емкость аккумуляторов для выравнива­ния графика тепловой нагрузки можно оп­ределять графическим методом, предло­женным А.В. Хлудовым [139].

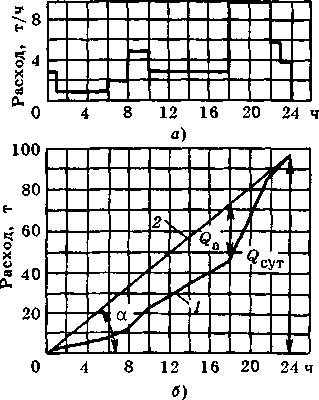
Сущность метода заключается в следую­щем. На основании суточного графика расхода теплоносителя (рис. 8.19, а) стро­ится интегральный график расхода 1 (рис. 8.19, б). Каждая ордината интеграль­ного графика расхода равна суммарному расходу теплоносителя от начала суток до момента, соответствующего указанной ор­динате. Интегральным графиком подачи при суточном выравнивании расхода тепло­носителя является прямая 2, соединяющая начало координат с конечной ординатой су­точного интегрального графика расхода. Угловой коэффициент интегрального гра­фика подачи равен среднечасовой подаче теплоносителя

tga ⁼ (?_cyT/24,

где (?_сут —суточный расход теплоносителя.

Емкость аккумулятора Q_a, требующаяся для указанного выравнивания нагрузки,