Статья по теме: критическое мышление. Ического мышления учащихся, мы проанализировали фгос по математике для основной школы и учебные материалы, используемые в школе
 Скачать 203.78 Kb. Скачать 203.78 Kb.
|
|
Для эффективного процесса обучения, который способствует развитию критического мышления учащихся, мы проанализировали ФГОС по математике для основной школы и учебные материалы, используемые в школе (учебник и дидактические работы по математике 5 класса авторы: Н.Я. Виленкин, В.И. Жохов, А.С. Чесноков, С.И. Шварцбурд). В ФГОС результатом изучения математики являются: развитие у учащихся способностей к анализу и нахождению нужной информации в тексте; самостоятельное планирование своей деятельности для достижения цели; умение оценивать правильность своих действий; самоанализ, самоконтроль и самооценка; развитие умений четко формулировать свои мысли как письменно, так и устно. Данные способности учеников, доказывает, что на уроках необходимо использовать разнообразные приемы для развития критического мышления. Нами предпринята попытка разработать модель развития критического мышления в преподавании математики. Модель построена на основе принципа систематичности, то есть вся структура едина и имеют логическую структуру. Содержание модели основывается на анализе ранее изученной психолого-педагогической литературы.   Модель содержит пять компонентов: целевой, содержательный, организационно-методических, диагностико-коррекционный и результативный. Модель содержит пять компонентов: целевой, содержательный, организационно-методических, диагностико-коррекционный и результативный.
Первый компонент модели (целевой) связан с целеполаганием. В нем показана основная цель – развитие критического мышления учащихся. Второй компонент модели (содержательный) показывает основные понятия, на которые мы опираемся в своем исследование и компоненты критического мышления, которые необходимо развивать в учениках. На основе анализа научной литературы под мышлением мы понимаем процесс познавательной деятельности человека, который отражает предметы и явления в их существенных связях и отношениях. Под критическим мышлением мы понимаем разумное направленное, рефлексивное мышление в процессе приобретения собственных знаний, которое включает поиск путей рационального решения проблем, анализ и синтез, оценку чужой и собственной информации, выявление полезных аспектов (И. О. Зигашев). То есть критическое мышление – это интеллектуальную деятельность человека, направленная на: Открытие, анализ, синтез и оценку информации. Развитие собственной точки зрения и умение ее логически аргументировать и доказывать. Анализ результатов своей деятельности. Компоненты составляющие критическое мышление мы выбрали из статьи «Теоретические основы развития критического мышления младших школьников» Сергеева Б.В., Оганесян В.А., которые основывается на критериях и показателях, выделенных Д. Клустером. Когнитивный компонент. Характеризует способности учащихся такие как: знание предмета, восприятие учебного материала. Аналитический компонент. Включает в себя: логичность (каждую информацию нужно проверять с точки зрения логики), рефлексию (процесс самопознания себя), оценку утверждений (показывает ценность какого-либо предмета или объекта). Личностный компонент. Включает в себя: толерантность (терпеливое отношение к чужому мнению), скептицизм (недоверчивое отношение к каким-либо знаниям), самостоятельность (умение самостоятельно поставить себе цель и добиться ее своими силами), прагматичность (способность выстраивать свою систему взглядов на жизнь), интегративность (объединение в целое ранее полученных однородных знаний). Деятельностный компонент. Включает умения, которые способствуют развитию критического мышления, то есть умение решать проблему, строить прогнозы, поиск логических ошибок и другие. В третьем компоненте модели (организационно-методический) рассматриваются приемы и средства, используемые на уроках. На основе анализа психолого-педагогической литературы по приемам развития критического мышления, мы попробовали создать свои педагогические приемы. Первый прием – «Блок знаний» основан на приемах: тонкие и толстые вопросы, верные и не верные утверждения, блок-схема (кластеры). Ниже представлена суть нашего приема. Учащимся выдается индивидуальная карточка с блок-схемой, в каждой ячейке схемы ученики выполняют задание: решить пример, выбрать верное или неверное утверждение, ответить на вопрос, решить математический ребус и другие. Все задания даются разнообразные, чтобы ученики смогли проверить свои знания по изучаемой теме. В зависимости от ответа ученик переходит на следующий этап. Таким образом учащиеся приходят к концу схемы, где на основе результатов выводят ответ на поставленный вопрос. Если ученики работают в парах, то каждому варианту выдается свое задание и итогом работы будет являться совместный ответ учеников, составленный по полученным результатам в заданиях. Аналогично происходит и при работе в группах по 4 человека, каждый работает со своей блок-схемой и в итоге приходят к совместному ответу. В конце коллективных обсуждений, ученики возвращаются к своим карточкам и анализируют свои действия, проверяют все ли верно решено, какие пробелы в знаниях есть и, что нужно повторить и подтянуть. Прием интересен учащимся, так как они быстро вливаются в процесс решения заданий и хотят прийти к результату быстрее, чем их одноклассники. Используя прием на уроках у учащихся развивается критическое мышление, так как во время работы с блок-схемой ученики анализируют и ищут новую информацию для решения заданий; при обсуждениях и составления ответов аргументируют и доказывают свою точку зрения; в конце работы с блок-схемой проводят рефлексию, то есть анализируют свою деятельность. Второй прием – «Математическая сумма». Прием основан на таких приемах как тонкие и толстые вопросы, ассоциации, корзина идей, мозговой штурм. Прием используется на стадии «вызов» для актуализации знаний. Учащимся в начале урока представлены две или три картинки, которые соединены между собой одной из четырех арифметических операций. Ученикам необходимо с помощью ассоциаций понять какой термин, математическое слово загадано. Сначала они записывают свои варианты ответов в тетрадях, а затем предлагают их классу и доказывают, что их ответ верный. Во время обсуждений учитель записывает все предположения учащихся на доску. В конце учитель показывает верный вариант ученикам и просит аргументировать учащихся, что оставшиеся варианты не верны. Данный прием способствует развитию: Синтеза информации. Собственной точки зрения и умению аргументировать ее. Терпеливости к чужому мнению. Исходя из выше выбранных приемов, мы выбрали средства, которые способствуют эффективному учебному процессу: раздаточный материал, таблицы, презентации. В данном компоненте еще мы описали формы работы: учащиеся работают не только индивидуально, но и в группах, что способствует повышению у них ранее описанных компонентов критического мышлению. Используя приемы и средства обучения, учитель может проводить как традиционные уроки, так и нетрадиционные (нестандартные). Взаимосвязь ученика с учителем, показанная в модели стрелкой, говорит о том, что их деятельности направлена на развитие личности учащихся, на взаимопомощь, взаимопонимание. Четвертый компонент модели (диагностико-коррекционный компонент) представляет собой диагностику уровней развития критического мышления учащихся. В результате которой выделяются три уровня критического мышления с учетом компонентов входящих в нее: высокий, средний, низкий. Если у ученика в процессе не наблюдается повышения уровня развития критического мышления, посредством использования промежуточных методик проверки уровня развития, то необходимо корректировать учебный процесс, то есть возвращаться на второй и третий компонент модели. Данная коррекция может быть индивидуальной или групповой, в зависимости от результатов промежуточной проверки.
Пятый компонент модели (результативный) показывает результаты после использования выбранных нами приемов на уроках математики для развития критического мышления учащихся пятых классов. Проверка модели на базе МАОУ СОШ №40 г. Тюмени в течение 2019-2020 учебного года с учениками 5 «Б» и 5 «В» классах. Всего в исследование приняли 68 учеников (34 учащихся в экспериментальной группе и 34 в контрольной группе). Для проверки уровня развития критического мышления была выбрана методика определения уровня критического мышления (Ю. Ф. Гущин, Н. В. Смирнов). Данная методика была выбрана не случайно, так как с помощью нее можно определить не только общий уровень развития критического мышления. Цель методики – исследование в целом уровня критического мышления обучающихся. Методика включает 15 тестовых заданий, ученикам нужно дать ответы и обосновать их. Каждое задание оценивается в 3 балла, максимальное количество баллов – 45. В зависимости от количества полученных баллов выявляется уровень сформированности критического мышления: Высокий уровень, если ученик набирает больше 36 баллов, то есть 80 % заданий должны быть правильно выполнены. Средний уровень, если ученик набирает от 15 до 36 баллов, то есть от 33 % до 80 % правильных ответов. Низкий уровень, если ученик набирает меньше 15 баллов, то есть меньше 33 % правильных ответов. Использование данной методики до начала эксперимента, то есть проведения уроков с приемами развития критического мышления, позволило определить, что у учащихся двух классов в большинстве случаев: 64 % (22 ученика) и 61 % (21 ученик) низкий уровень сформированности критического мышления, средний уровень показали 12 учащихся в одной группе и 11 учащихся во второй группе, высокий уровень показали по 1 ученику в каждом классе. У контрольной группы уроки проводились в обычном режиме без использования приемов развития критического мышления, а в экспериментальной группе на большинстве уроков наоборот использовались выбранные и разработанные нами приемы. Задания и темы уроков основывались на календарно-тематическом планирование и учебнике по математике 5 класса авторы: Н.Я. Виленкин, В.И. Жохов, А.С. Чесноков, С.И. Шварцбурд. Содержание курса «математика» в 5 классе предполагает повторение курса начальной школы (натуральные числа: сложение, вычитание, умножение и деление), знакомство с новой и основной темой «Дроби», которая включает в себя: обыкновенные дроби, смешанные числа, десятичные дроби и арифметические действия с ними, а также «проценты». Исходя из анализа содержания для эксперимента были отобраны темы «обыкновенные дроби», «смешанные числа» и «десятичные дроби», которые больше всего подходят для использования приемов развития критического мышления и являются ключевыми в обучение математики в 5 классе. Рассмотрим несколько примеров использования выбранных нами приемов на уроках математики. В теме «правильная и неправильная дробь» на третьей стадии урока «рефлексия» был использован метод «синквейн». На слайд для учеников была выведена структура синквейна и пример по теме «математика в целом:
Все ученики справились с данным заданием, им понравилось творческое задание, каждый придумал свой оригинальный синквейн, один из них представлен в таблице. Прием «фишбоун» использовался на уроке умножение и деление десятичных дробей как способ закрепления полученных знаний учащихся. Учащимся было дано задание представить в виде рыбного скелета правила, изученные в данной главе учебника. Данное задание было выдана ученикам как домашнее во время дистанционного обучения, один из вариантов представления «фишбоун» учениками на РИСУНОК. Некоторые ученики помимо основных правил умножения и деления десятичных дробей, выписывали умножение и деление десятичных дробей на 10, 100, 1000 и 0,1, 0,01, 0,001. 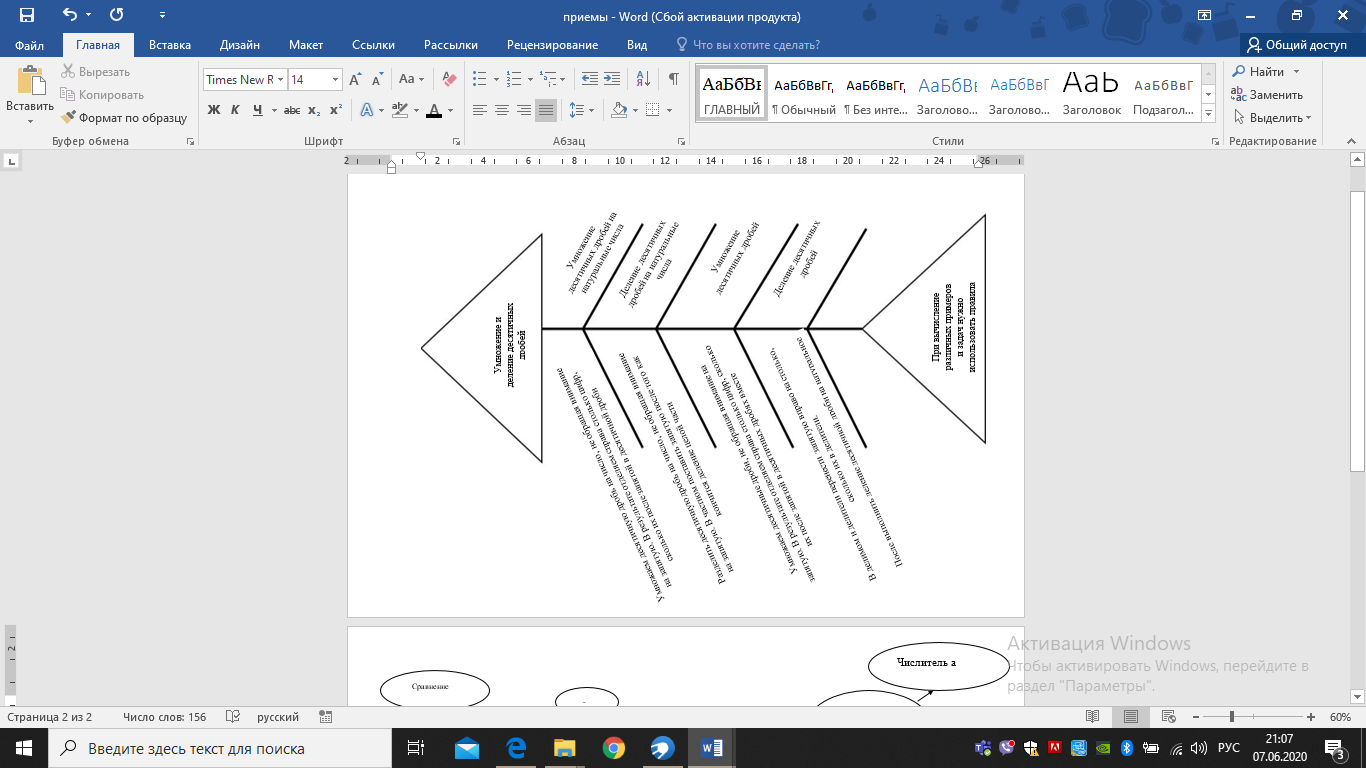 Диагностическая работа проводилась по той, что и на первом этапе эксперимента. После диагностики учащихся были обработаны и проанализированы результаты исследования.
По методики Ю. Ф. Гущина и Н. В. Смирнова видна большая разница между результатами начальной и контрольной диагностик. В начале эксперимента всего 1 ученик имел навыки критического мышления, но к концу эксперимента процент учащихся повысился на 32,4% и учеников с высоким уровнем развития критического мышления стало 12. Низкий уровень развития критического мышления на конец эксперимента показывают всего 5 учеников. В контрольной группе тоже увеличилось количество учеников с высоким и средним уровнями, но не так резко. Это доказывает, что уроки с использованием выбранных нами приемов проходили эффективно. Из результатов, полученных на контрольном этапе и сравнение их с результатами диагностик констатирующего этапа видно, что целесообразно использовать выбранные приемы на уроках математики для повышения уровня развития критического мышления учащихся. Уроки имели личностно-ориентированную направленность, ученики развивали навыки работы с изучаемым материалом, самостоятельно определяли цели учебной деятельности, составляли план для реализации цели. Также ученики составляли ребусы, сказки, кроссворды, задачи по конкретным темам и математики в целом. | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||

 Мышление
Мышление Ученик
Ученик