сопромат 33 каз. лекции. Іі блім материалдар кедергісі

• Название: Іі блім материалдар кедергісі
• Анкор: сопромат 33 каз. лекции.docx
• Дата: 10.04.2018
• Размер: 454.79 Kb.
• Имя файла: сопромат 33 каз. лекции.docx
• Тип: Документы; #17865
• страница: 3 из 3

§ 2.8. Созылу және сығылу кезіндегі материалдар кедергісінің негізгі есептеу өрнектері

№ п/п	Шаманың немесе шарттың атауы	Белгілеуі	Өрнегі
1.	Бойлық күші	N	Кесілген бөлшектің тепе-теңдігінің теңдеуі
2.	Тік кернеуі	s	s = N/A
3.	Абсолюттік ұзаруы	Dl	Dl = l¢ - l
4.	Салыстырмалы бойлық деформациясы	e	e =
5.	Гук заңы		s = e Е Dl =
6.	Бойлық және көлденең деформациялар араларындағы тәуелдік		e¢ = - n e
7.	Беріктік шарты		s = N/A £ sadm
8.	Көлденең қималардың орын ауыстыруы	w
9.	Қатаңдық шарты		emax £ eadm D lmax £ D ladm
10.	Деформацияның потенциалдық энергиясы	U

Бақылау сұрақтары:

1. 
   Ауданның статикалық моменті дегеніміз не? Өлшемі қандай?
   
2. 
   Орталық өстерге қатысты ауданның статикалық моменті қандай?
   
3. 
   Салмақ центрінің координаттары арқылы ауданның статикалық моменті қалай есептеледі?
   
4. 
   Өстік,полярлық,центрдентепкіш инерция моменті дегеніміз не?Өлшемі қандай? Таңбалары қандай?
   
5. 
   Координат өстерін параллель көшіргенде инерция моменттері қалай өзгереді?
   
6. 
   Координат өстері бұрылғанда инерция моменттері қалай өзгереді?
   
7. 
   Қай өстер бас инерция өстері деп аталады? Олардың орналасуы қалай анықталады?
   
8. 
   Қандай моменттер инерция бас моменттері деп аталады? Олар қалай есептеледі?
   

9.Тіктөртбұрыштың,дөңгелектің,сақинаның,үшбұрыштың инерция моменттері қалай есептеледі?

10. Инерция радиусы дегеніміз не?

11. Күрделі фигуралардың,таптау кескіндердің инерция моменттері қалай есептеледі?
3 Тарау. Жазық қималардың геометриялық сипаттамалары
§ 3.1. Негізгі түсініктер
1М. Бір ұшы қатаң бекітілген тіктөртбұрыш қималы сырықтың бос ұшында қадалған F күші әсер етеді. 3.1 а – б суреттерінде қиманың күштің әсер ету сызығына қатысты орналасуы және сырықтың деформацияланған өсі көрсетілген.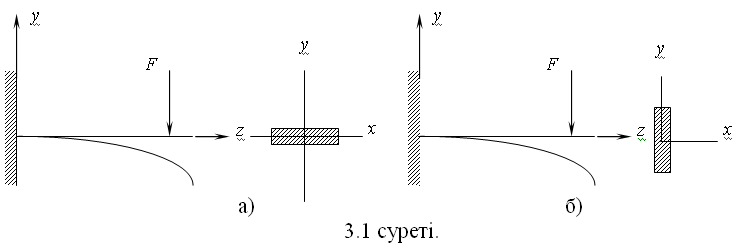



Келтірілген мысал, сырық өлшемі және әсер етуші күш өзгерілмей,тек қиманың F әсер ету сызығына қатысты орналасуы өзгерсе, сырықтың деформациясы өзгергенін, көрсетеді.

Жазық фигураның координат өстерге қатысты орналасуына тәуелді геометриялық сипаттамаларын енгізейік (3.2суреті):

А ауданының х және у координат өстеріне қатысты статикалық моменттері деп келесі өрнектермен анықталатын шамалар аталады:

(3.1)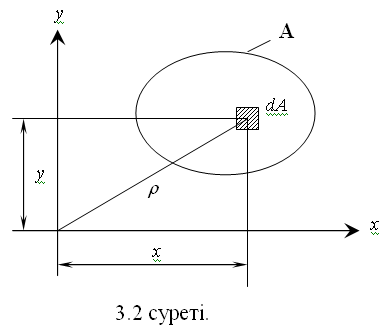



Ауданның статикалық моменттерінің өлшемі-см³, мм³, м³.

Егер жазық фигураның салмақ центрі белгілі болса,онда статикалық моменттер S_x, S_y салмақ центрінің координаттары х_с, у_с және фигура ауданы А арқылы есептеледі

S_x = Ау_с, S_y = Ах_с. (3.2)
Егер жазық фигураның салмақ центрі С арқылы х₀, у₀,координат өстерін (орталық өстері) өткізсек,онда орталық өстерге қатысты А ауданының статикалық моменттері нөлге тең.

А ауданының х және у координат өстеріне қатысты инерция моменттері деп келесі өрнектермен анықталатын шамалар аталады: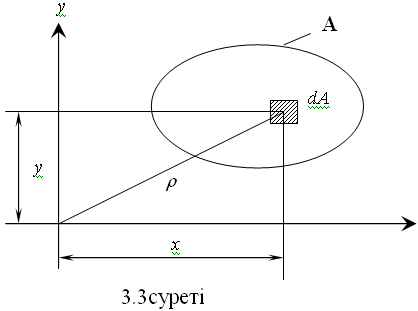




Жазық фигураның полярлық инерция моменті деп келесі шама аталады

(3.4)

J_x + J_y = J_r. 3.3 суретінен көрінеді.

Жазық фигураның центрдентепкіш инерция моменті деп келесі өрнекпен анықталатын шама аталады

(3.5)

Барлық инерция моменттерінің өлшемі – м⁴, см⁴, мм⁴. Келтірілген анықтамалар бойынша J_r, J_x, J_y тек оң таңбалы, ал S_x, S_y,J_xyоң,теріс және нөлге тең болуы мүмкін.
§ 3.2. Қарапайым фигуралардың инерция моменттері

Қарапайым фигураларға тіктөртбұрыш, дөңгелек, сақина,үшбұрыш жатады.

1. Тіктөртбұрыш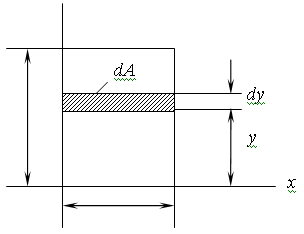
(3.6)
2.Дөңгелек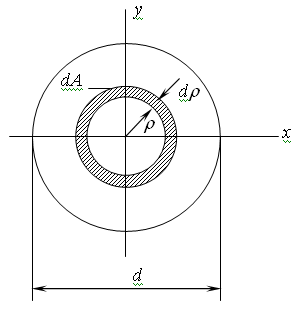
(3.7)

3. Сақина

(3.8)

4. Үшбұрыш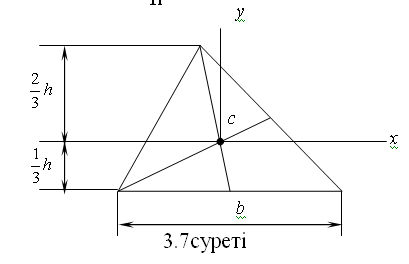

(3.9)
§ 3.3. Өзара параллель өстерге қатысты инерция моменттерінің тәуелдігі
Есеп шарты: Жазық фигураның x және y координат өстеріне қатысты геометриялық сипаттамалары J_x, J_y, J_xy S_x, S_y, J_xy, А белгілі. х, у өстеріне параллель х¢, у¢, өстеріне қатысты геометриялық сипаттамаларын анықтау керек.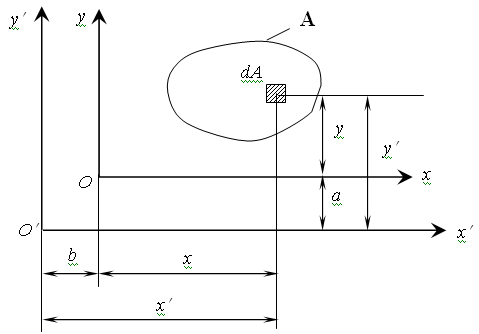

3.8суреті.
Берілгені: J_x, J_y, J_xy

S_x, S_y, S_xy

a, b

––––––––––––––

J_x¢, J_y¢, J_x¢y¢ – ?


(3.3) және (3.5)-ті пайдалана отырып, келесі нәтижеге келеміз:

(3.10)

(3.10) өзара параллель өстерге қатысты инерция моменттері арасында тәуелдікті көрсетеді.

Егер алғашқы өстер х, у орталық өстер болса,онда S_x = S_y = 0,ал (3.10) өрнектері келесі түрге келеді:

(3.11)
§ 3.4. Координат өстері бұрылған кездегі инерция моменттерінің өзгеруі
Есеп шарты: Жазық фигураның x және y координат өстеріне қатысты геометриялық сипаттамалары J_x, J_y, J_xy белгілі. х, у өстері координат басына қатысты a бұрышына бұрылған кезде пайда болған u және v өстерге қатысты геометриялық сипаттамаларын анықтау керек.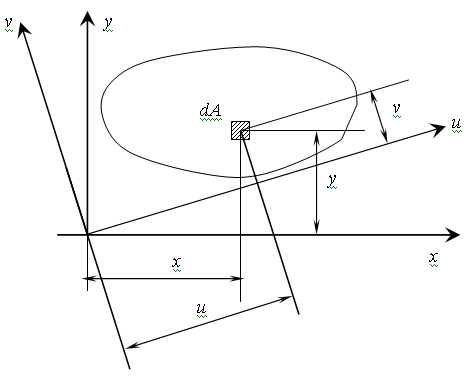

3.9суреті.

Берілгені:

J_x, J_y, J_xy.

a

–––––––––––

J_u, J_v, J_uv – ?
Элементарлық dAауданның ескі және координат жүйелеріндегі координаттары келесі тәуелдікпен байланысты
u = x cosa + y sina,

v = -x sina + y cosa
(3.3) және (3.5)-ке сүйеніп, (*)-пайдаланып,келесі нәтижеге келеміз:
J_u = J_x cos²a + J_y sin²a - J_xy sin2a,

J_v = J_x sin²a + J_ycos²a + J_xy sin2a, (3.12)

J_uv = ( J_x - J_y)sin2a + J_xy sin2a.

(3.12) – координат өстері бұрылған кездегі,инерция моменттерінің өзгеруі.

(3.12) – О центрінен өтетін өстер түйініне қатысты инерция моменттерін анықтайды.
§ 3.5. Инерция бас өстері,бас инерция моменттері.Бас инерция радиусы
О центрінен өтетін координат өстерінің жиынтығының арасында өзара перпендикуляр екі өс бөлінеді.Ол өстердің жеке қасиеттері бар:

1⁰. Өстерге қатысты центрдентепкіш инерция моменті нолге тең.

2⁰. Өстердің біріншісіне қатысты инерция моменті максималды,ал екіншісіне қатысты– минималды мәніне жетеді.

Аталған ерекшілігі бар өстер инерция бас өстері деп,ал сол өстерге қатысты инерция моменттері инерция бас моменттері деп аталады.

Инерция бас өстерінің орналасу жағдайын аталған қасиеттеріне сүйене отырып анықтаймыз:

(3.13)
(3.13) өрнегінен екі бұрыш және = + 90 анықталады. және бұрыштардың мәндерін (3.12)-дегі J_u, J_v-ке қойып ,инерция бас моменттерін табамыз

(3.14)

«+» таңбасы J_max-қа сәйкес,ал «–»таңбасы – J_min.

Көзге көрінер келесі:

1. Симметриялық фигуралардың симметрия өсі инерция бас орталық өстерінің біреуі болады,ал екіншісі салмақ центрінен симметрия өсіне перпендикуляр болады.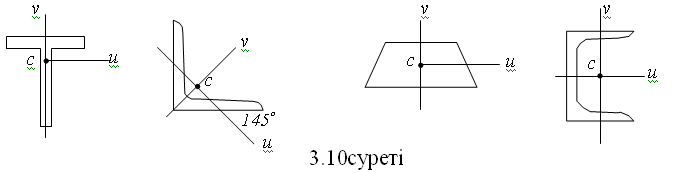

2. Егер жазық фигураның екі симметрия өсі бар болса,онда аталған өстер инерция орталық бас өстері болады.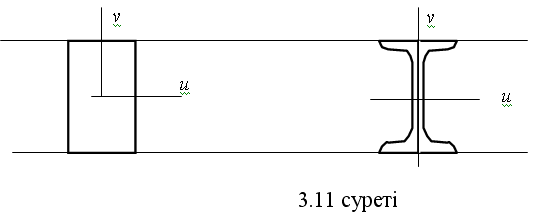


3. Егер жазық фигураның екі инерция орталық бас моментті бір біріне тең болса,ондай фигураның кез келген орталық өсі инерция бас өсі болып келеді және барлық орталық бас инерция моменттері бір біріне тең (дөңгелек, квадрат, дұрыс алтыбұрыштық, теңқабырғалы үшбұрыш).

Жазық фигураның өске қатысты инерция моментін инерция радиусы деп аталатын сызықты шаманың квадраты арқылы көрсетуге болады.Инерция бас өстеріне сәйкес инерция радиустары бас инерция радиустары деп аталады.

(3.15)

Таптау(илемделген темір бұйымдар) кескіндердің негізгі геометриялық сипаттамалары сұрыптама кестелерінде келтіріледі.
3.6. Күрделі фигуралардың инерция моменттері
Күрделі фигураның инерция моменті фигура бөлшектерінің инерция моментерінің қосындысына тең

J_x = (3.16)

Бұл жағдай анықталған интегралдың қасиеттерінен шешіледі

,

мұнда А = А₁ + А₂ + …

Сонымен,күрделі фигураның инерция моментін есептеу үшін,оны бірнеше қарапайым фигураға бөліп,сол фигуралардың инерция моменттерін есептеп,қосу керек.Аталған қасиет полярлық және центрдентепкіш инерция моменттері,ауданның статикалық моменттері үшін дұрыс.

Бақылау сұрақтары :

1. 
   Кедергінің қай түрі иілу деп аталады?
   
2. 
   Иілудің қандай түрлері кездеседі?
   
3. 
   Арқалық дегеніміз не?
   
4. 
   Арқалықтың көлденең қималарында қандай ІКФ-лері әсер етеді және олар қалай анықталады?
   
5. 
   q, Q_y, M_x араларында қандай дифференциалдық тәуелдіктер бар?
   
6. 
   а) Ұзындығы бойынша бірқалыпты таралған күшпен q; б) консоль ұшында қадалған күшпен жүктелген консольды арқалық үшін Q_y, M_x эпюрлерін салыңыз.
   
7. 
   Ортасында сыртқы қос күші әсер ететін екітіреулі арқалық үшін Q_y, M_x эпюрлерін салыңыз.
   
8. 
   Құрама арқалықтың Q_y, M_x эпюрлерінің ерекшілігі қандай?
   
9. 
   Егер: а) арқалық аралығында бірқалыпты таралған q күші әсер етсе ; б) арқалық аралығында бірқалыпты таралған q күші жоқ болса; в) егер арқалық қимасында қадалған F күші әсер етсе ; г) егер арқалық қимасында сыртқы момент Mәсер етсе Q_y, M_x эпюрлерінің түрлері қандай?
   

10. 
    Иілім деген не?
    
11. 
    Қиманың бұрылу бұрышы деп қандай шаманы атайды?
    
12. 
    Қиманың бұрылу бұрышы мен иілімнің араларында қандай байланыс бар?
    
13. 
    Иілген өстің нақты дифференциал теңдеуі қандай тәуелдіктің негізінде шығарылады?
    
14. 
    Иілген өстің жуықты дифференциал теңдеуінің түрі қандай? Бұл теңдеудегі «±» таңба неден тәуел?
    
15. 
    Тікелей интегралдаудау әдісінің мәні қандай?
    
16. 
    Интегралдаудың тұрақтылары қандай шарттардан анықталады ?
    
17. 
    Топсалы тіреу және қатаң бекіту үшін тіреу шарттары қандай ?
    
18. 
    Бастапқы параметрлер дегеніміз не?
    
19. 
    Бастапқы параметрлер әдісінде қолданатын арнайы әдістер қандай?
    
20. 
    Қатаңдық шартын жазыңыз .
    
21. 
    Мүмкіндік иілімді қалай таңдайды?