Эконометрика- задачи. Имеются следующие данные о выработке литья на одного работающего Х
 Скачать 1.76 Mb.
|
   Получили уравнение множественной регрессии: Y = 206,522 – 1,352 · х1 + 11,8 · х2 Коэффициент множественной корреляции равен 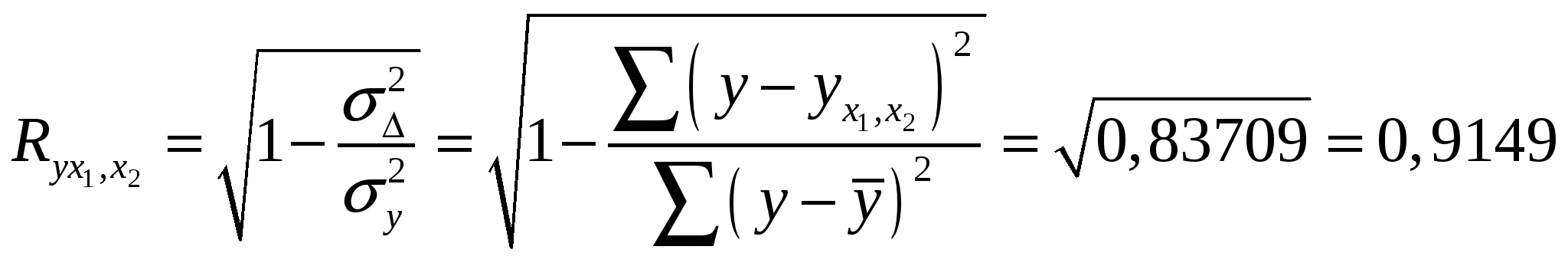 - связь сильнаяКоэффициент множественной детерминации равен 0,8371 или 83,71%, т.е. 83,71% вариации себестоимости 1 т литья объясняется за счет изменения выработки литья на одного работающего и брака литья. 3) оценим значимость полученных уравнений на уровне = 0,05. Уравнение парной линейной регрессии у = 283,056 – 1,617·x: 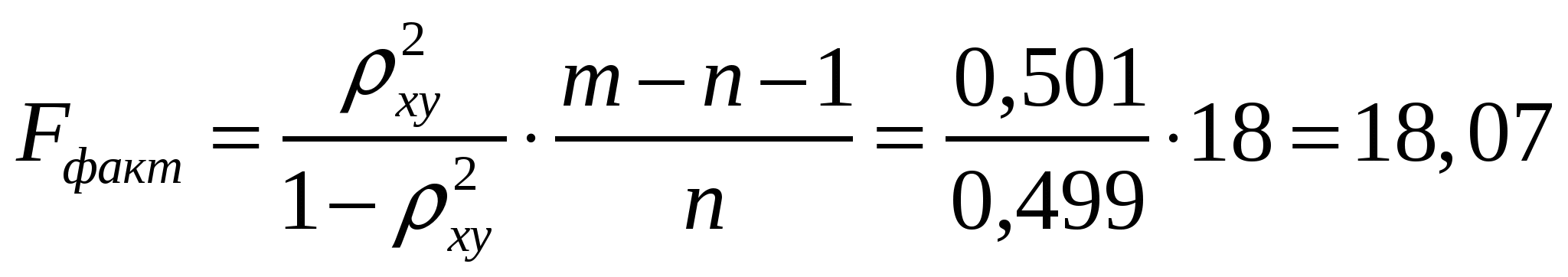 Fтабл = 4,35 < Fфакт, при а = 0,05. Следовательно, отклоняется гипотеза Н0о статистически незначимых параметрах этого уравнения. Уравнение множественной регрессии Y = 206,522 – 1,352 · х1 + 11,8 · х2 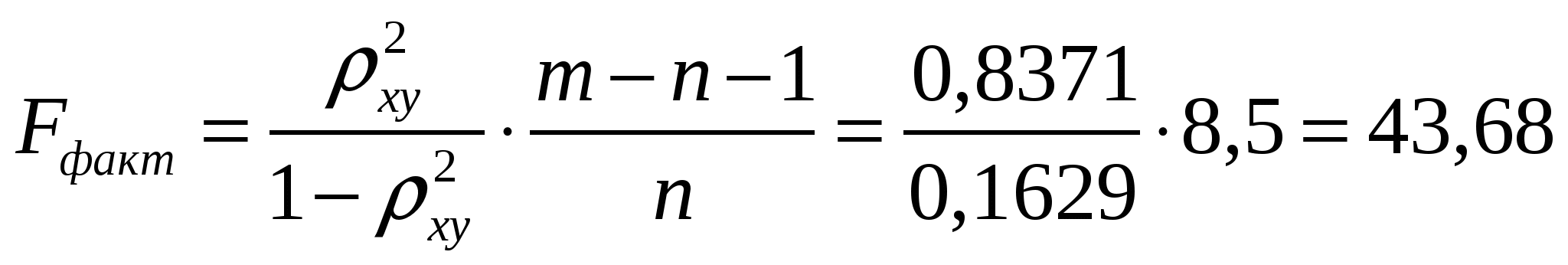 Fтабл = 4,41 < Fфакт, при а = 0,05. Таким образом, отклоняется гипотеза Н0о статистически незначимых параметрах этого уравнения. 4) установим значимость коэффициента регрессии при X2 на уровне = 0,05: Оценку статистической значимости параметра регрессии а2 проведем с помощью t-статистики Стьюдента. Выдвигаем гипотезу H0 о статистически незначимом отличии показателя от нуля:  tтабл для числа степеней свободы  и  составит 2,101.Определим случайную ошибку 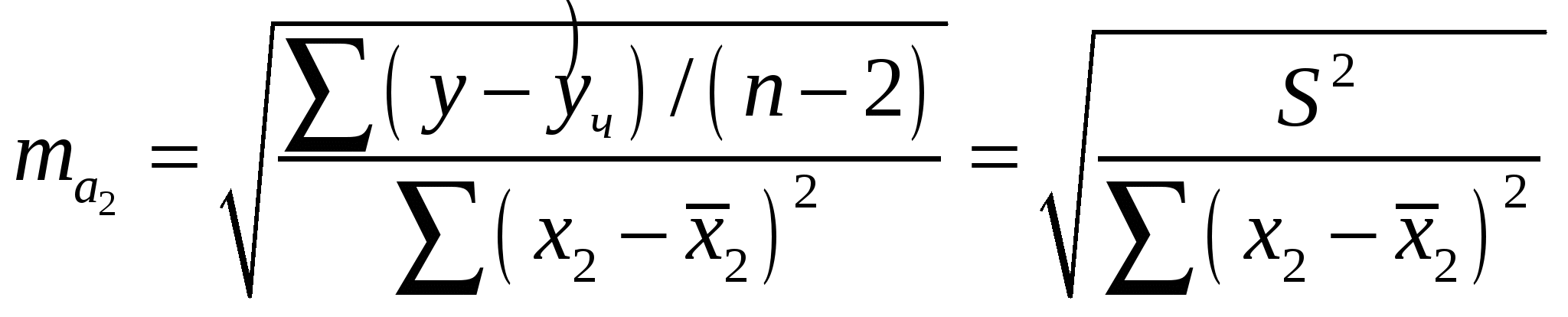 : ,где S2 – остаточная дисперсия на одну степень свободы, 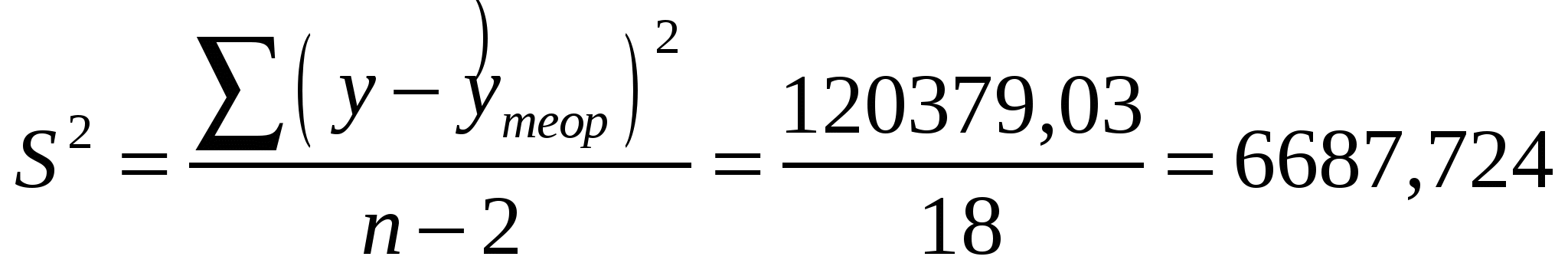 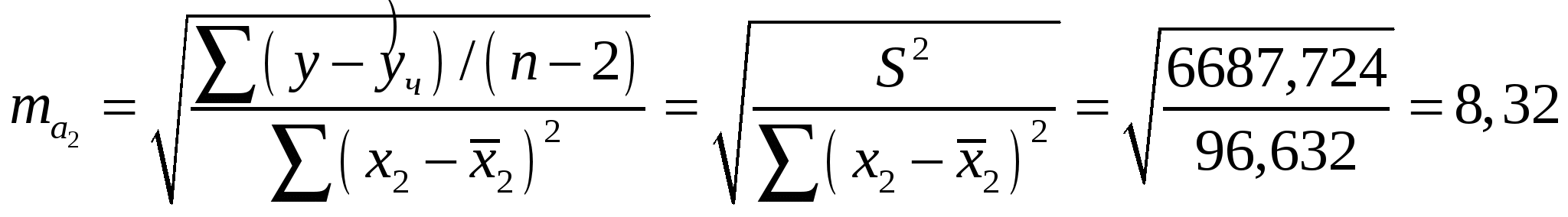 Тогда  .Фактическое значение t-статистики ниже табличного значения:  поэтому гипотеза H0 принимается, т.е. параметр а2 случайно отличается от нуля и статистически незначим. 5) получим точечную оценку среднего значения себестоимости 1т литья в цехах, в которых выработка литья на одного работающего составляет 40 т, а брак литья составляет 5%: Y = 206,522 – 1,352 · 40 + 11,8 · 5 = 206,522 - 54,08 + 59 = 211,442 (руб.) Задание 2. Имеются следующие данные о численности населения США в 1950-1985 гг. (млн. чел.)
Требуется обработать эти данные, выполнив следующие действия:
Решение. 1) Построим график динамического ряда. По оси Х откладываем годы, по оси Y – численность населения, млн. чел.: 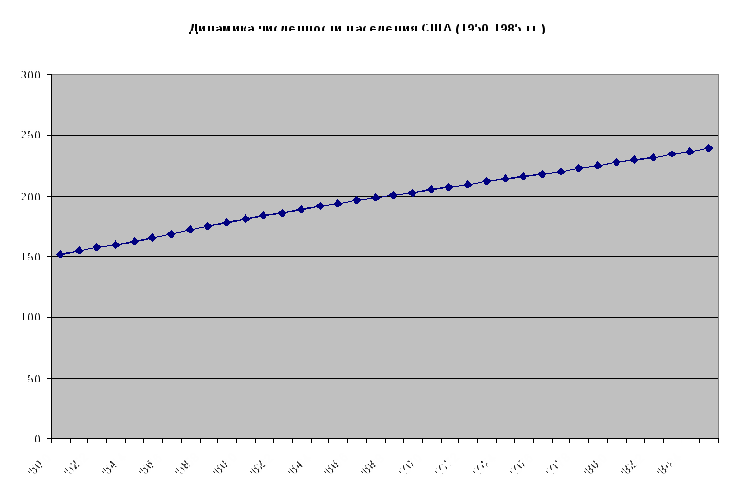 График показывает увеличение численности населения США и позволяет предположить линейную форму тренда изучаемого показателя. 2) В данном случае для выражения основной тенденции мы применим метод аналитического выравнивания по прямой. Для выравнивания ряда динамики по прямой используем уравнение  .Способ наименьших квадратов дает систему двух нормальных уравнений для нахождения параметров  и  : где у – исходный уровень ряда динамики; n – число уровней ряда; t – показатель времени, который обозначается порядковыми номерами, начиная от низшего.   Для того, чтобы упростить технику расчета, мы придадим показателям времени t такие значения, чтобы их сумма была равна нулю:  . В нашей задаче число уровней ряда четное (n = 36), поэтому учет времени будет вестись полугодиями. При этом уравнения системы примут следующий вид: и  ,откуда  - представляет собой средний уровень ряда динамики ( ); .В результате получаем следующее уравнение основной тенденции изменения численности населения США в период с 1950 по 1985 г.:  , где t – порядковый номер полугодия.3) Удалим трендовую составляющую из временного ряда и построим график остатков. Расчетные данные представим в таблице:
|