вкр. ВКР Лазарева. Имитационное моделирование систем массового обслуживания с динамическим приоритетом
 Скачать 1.02 Mb. Скачать 1.02 Mb.
|
Глава 2. Математическое описание модели§2.1. Постановка задачиРассмотрим многоканальную СМО, в которую поступают заявки двух типов: первый тип – главные, но поступающие редко заявки, второй тип – второстепенные, но зачастую поступающие заявки, которые при этом невозможно терять. Заявки обоих типов поступают самостоятельно друг от друга и образуют простейшие потоки с интенсивностями 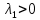 , , 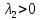 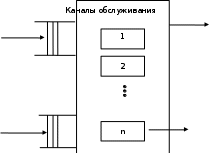 Рис.2.Схема СМО. Обслуживают заявки 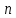 операторов имеющих одинаковую квалификацию со средним временем обслуживания операторов имеющих одинаковую квалификацию со средним временем обслуживания 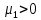 для первого типа заявок и для первого типа заявок и 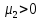 для второго. Для всего типа заявок формируется отдельная неограниченная очередь. для второго. Для всего типа заявок формируется отдельная неограниченная очередь.Всеобщая очередь в данном случае, видимо, не результативна, поскольку в таком случае главные, но редкие заявки первого типа будут долго ожидать начала обслуживания, что может быть недопустимо. Иные стратегии распределение источника (в данном случае 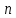 операторов), такие как стратегия абсолютного приоритета или стратегия подвижной границы [26], [37] также не результативны, так как допускают либо потери заявок второго типа либо большую часть времени операторы, зарезервированные под заявки первого типа, будут простаивать. операторов), такие как стратегия абсолютного приоритета или стратегия подвижной границы [26], [37] также не результативны, так как допускают либо потери заявок второго типа либо большую часть времени операторы, зарезервированные под заявки первого типа, будут простаивать.Следственно, предложена дальнейшая тактика с динамическим приоритетом. Заявки первого типа имеют относительный приоритет (ждут окончания обслуживания текущей заявки и после этого встают на внеочередное обслуживание). После обслуживания заявки первого типа приоритет переходит к заявкам второго типа, если есть заявки второго типа в очереди для заявок второго типа. Если заявок второго типа в очереди нет, то приоритет остается у заявок первого типа. Подобно, после выхода из СМО обслуженной заявки второго типа приоритет переходит к заявкам первого типа, если есть заявки первого типа в соответствующей очереди. Если заявок первого типа в очереди нет, то приоритет остается у заявок второго типа. То есть при наличии заявок обоих типов заявки проходят на обслуживание «через одного», а при отсутствии заявок одного из типов (заявки первого типа реже по условию) приоритет (очередность) не передается. Таким методом достигается приемлемое среднее время ожидания начала обслуживания для редких, но главных заявок первого типа при отсутствии необслуженных заявок второго типа и минимальных простоях операторов. §2.2. Математическая модель1. Опишем сначала работу по обработке заявок первого типа. Введем считающие процессы: 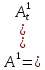 - число заявок первого типа, поступивших в систему за время - число заявок первого типа, поступивших в систему за время 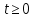 , , 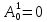 ; ; 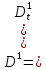 - число обслуженных заявок первого типа за время - число обслуженных заявок первого типа за время 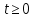 , , 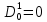 . .Точечные процессы 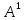 , ,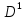 определяются своими компенсаторами определяются своими компенсаторами 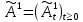 и и 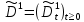 в соответствии с разложением Дуба-Мейера для субмартингалов [29]: в соответствии с разложением Дуба-Мейера для субмартингалов [29]: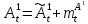 , (1) , (1)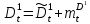 , (2) , (2)где 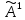 и и 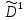 – неубывающие предсказуемые процессы – неубывающие предсказуемые процессы 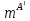 и и 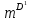 – мартингалы. – мартингалы.Для рассматриваемой в данной работе системы 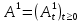 – пуассоновский процесс с компенсатором: – пуассоновский процесс с компенсатором: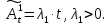 (3) (3)Компенсатор для процесса 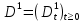 определяется следующим соотношением: определяется следующим соотношением: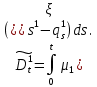 (4) (4)Здесь 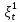 – число заявок первого типа в СМО в момент времени – число заявок первого типа в СМО в момент времени 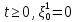 (в очереди или на обслуживании), (в очереди или на обслуживании), 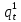 – число заявок первого типа в очереди в момент времени – число заявок первого типа в очереди в момент времени 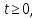 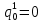 . Соответственно . Соответственно 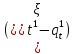 это число заявок первого типа, находящихся непосредственно на обслуживании в момент времени это число заявок первого типа, находящихся непосредственно на обслуживании в момент времени 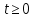 . .Кроме этого, для 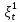 в момент времени в момент времени 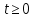 можно написать следующее основное балансовое соотношение: можно написать следующее основное балансовое соотношение: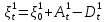 . (5) . (5)2. Аналогично опишем работу по обработке заявок второго типа. Введем считающие процессы: 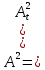 - число заявок второго типа, поступивших в систему за время - число заявок второго типа, поступивших в систему за время 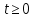 , , 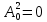 ; ; 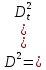 - число обслуженных заявок второго типа за время - число обслуженных заявок второго типа за время 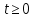 , , 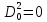 . .Точечные процессы 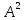 , ,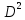 также определяются своими компенсаторами также определяются своими компенсаторами 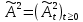 и и 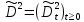 : :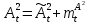 , (6) , (6)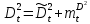 , (7) , (7)где 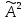 и и 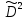 – неубывающие предсказуемые процессы – неубывающие предсказуемые процессы 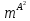 и и 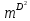 – мартингалы. – мартингалы.Аналогично 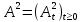 – пуассоновский процесс с компенсатором: – пуассоновский процесс с компенсатором: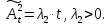 (8) (8)Компенсатор для процесса 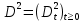 определяется следующим соотношением: определяется следующим соотношением: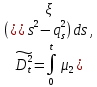 (9) (9)Здесь 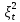 – число заявок второго типа в СМО в момент времени – число заявок второго типа в СМО в момент времени 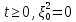 (в очереди или на обслуживании), (в очереди или на обслуживании), 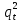 – число заявок второго типа в очереди в момент времени – число заявок второго типа в очереди в момент времени 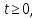 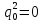 . .Для 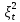 в момент времени в момент времени 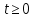 также можно написать основное балансовое соотношение: также можно написать основное балансовое соотношение: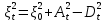 . (10) . (10)3. Опишем управление приоритетом через регулирование размеров очередей. Для размера очереди из заявок первого типа 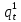 в момент времени в момент времени 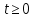 можно написать следующее балансовое уравнение: можно написать следующее балансовое уравнение: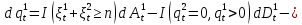 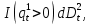 (11) (11)где 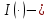 индикаторная функция, индикаторная функция, 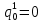 . Логика построения уравнения (11) следующая. Во-первых, размер очереди заявок первого типа . Логика построения уравнения (11) следующая. Во-первых, размер очереди заявок первого типа 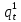 может увеличиться на одну заявку, если поступит заявка первого типа ( может увеличиться на одну заявку, если поступит заявка первого типа (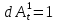 ) в момент, когда все ) в момент, когда все 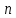 операторов заняты ( операторов заняты (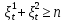 ). Во-вторых, размер очереди заявок первого типа ). Во-вторых, размер очереди заявок первого типа 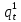 может уменьшиться на одну заявку, если закончится обслуживание заявки первого типа ( может уменьшиться на одну заявку, если закончится обслуживание заявки первого типа (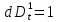 ), заявок второго типа в очереди нет ( ), заявок второго типа в очереди нет (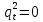 ), а заявки первого типа в очереди есть ( ), а заявки первого типа в очереди есть (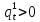 ). В-третьих, размер очереди заявок первого типа ). В-третьих, размер очереди заявок первого типа 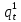 может уменьшиться на одну заявку, если закончится обслуживание заявки второго типа ( может уменьшиться на одну заявку, если закончится обслуживание заявки второго типа (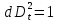 ) и есть заявки первого типа в очереди ( ) и есть заявки первого типа в очереди (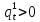 ). ).Аналогичное уравнение верно и для размера очереди из заявок второго типа 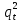 : :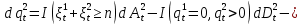 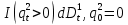 . (12) . (12)Логика построения уравнения (12) полностью совпадает с предыдущей формулой. Во-первых, размер очереди заявок второго типа 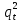 может увеличиться на одну заявку, если поступит заявка второго типа ( может увеличиться на одну заявку, если поступит заявка второго типа (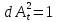 ) в момент, когда все ) в момент, когда все 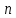 операторов заняты ( операторов заняты (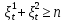 ). Во-вторых, размер очереди заявок второго типа ). Во-вторых, размер очереди заявок второго типа 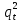 может уменьшиться на одну заявку, если закончится обслуживание заявки второго типа ( может уменьшиться на одну заявку, если закончится обслуживание заявки второго типа (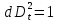 ), заявок первого типа в очереди нет ( ), заявок первого типа в очереди нет (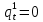 ), а заявки второго типа во второй очереди есть ( ), а заявки второго типа во второй очереди есть (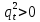 ). В-третьих, размер очереди заявок второго типа ). В-третьих, размер очереди заявок второго типа 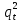 может уменьшиться на одну заявку, если закончится обслуживание заявки первого типа ( может уменьшиться на одну заявку, если закончится обслуживание заявки первого типа (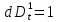 ) и есть заявки второго типа в очереди ( ) и есть заявки второго типа в очереди (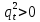 ). ). |
