вкр. ВКР Лазарева. Имитационное моделирование систем массового обслуживания с динамическим приоритетом
 Скачать 1.02 Mb. Скачать 1.02 Mb.
|
Глава 1. Теоретическая часть§1.1. Понятие СМОСистемой массового обслуживания (СМО) называется комплекс взаимосвязанных элементов, состоящий из некоторого числа обслуживающих единиц (каналов), в котором происходит удовлетворение массовых запросов (требований), поступающих в систему в случайные моменты времени. Обслуживание каждой заявки длится в течение некоторого случайного времени и зависит от показателей эффективности системы. После того, как заявка обслужена, она покидает канал, и система готова к приему очередной заявки. Примеры СМО - телефонная станция, автостоянка, кассир магазина, служба занятости. Основные элементы СМО - источник требований, входящий поток заявок, каналы обслуживания, выходящий поток заявок. Предметом теорииСМО является построение математических моделей (т. е. образов реального экономического объекта, описанных с помощью уравнений, формул, графиков, схем и т. д.) для теоретического анализа и практического использования свойств СМО. Показатели эффективности СМО - характеристики работы системы, описывающие ее способность справляться с потоком заявок. Эффективность функционирования СМО описывается такими показателями: 1) Эффективность использования СМО - абсолютная или относительная пропускные способности системы, среднее число занятых каналов (коэффициент использования СМО), средняя продолжительность использования СМО, интенсивность нагрузки канала; 2) Качество обслуживания заявок - среднее число заявок, обслуженных СМО в единицу времени, вероятность простоя системы, вероятность отказа в обслуживании, среднее число заявок в очереди, среднее число заявок в системе и др.  Рис.1: Многоканальная СМО. Поток заявок, поступающих в систему, характеризуется интенсивностью 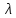 , то есть частотой появления заявок в системе, или средним числом заявок, поступающих в систему в единицу времени. , то есть частотой появления заявок в системе, или средним числом заявок, поступающих в систему в единицу времени.Интенсивность μ потока обслуживаний - это величина, обратная среднему времени обслуживания, или число заявок, обслуженных системой в единицу времени. Интенсивность нагрузки канала обслуживания ρ, - это величина, показывающая среднее число заявок, поступающее в систему за среднее время обслуживания одной заявки: 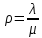 . . При этом его экономический смысл заключается в том, что показатель ρ, - это среднее число каналов, которое необходимо иметь, чтобы обслуживать в единицу времени все поступающие в систему требования. Условие 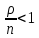 , , где n - число каналов обслуживания, означает, что необходимое число каналов обслуживания должно быть больше ρ. §1.2. Классификация СМОПо дисциплине обслуживания: — СМО с отказами, когда заявка, поступившая в систему в момент, когда все каналы заняты, остается необслуженной; — СМО с ожиданием (очередью), в которых заявка в случае занятости всех каналов становится в очередь и ожидает обслуживания; — Системы с ограничением длины очереди; — Системы с ограниченным временем ожидания; По месту нахождения источника требований: — Замкнутые СМО, когда источник требований находится в самой системе; — Открытые СМО, когда источник требований находится вне системы; По числу обслуживающих каналов: — Одноканальные; — Многоканальные. §1.3. Пуассоновский процессТочечным (считающим) процессом 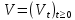 на некотором стохастическом базисе на некотором стохастическом базисе 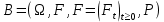 называется неубывающий процесс с называется неубывающий процесс с 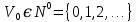 , кусочно-постоянными траекториями, допускающий только единичные скачки , кусочно-постоянными траекториями, допускающий только единичные скачки 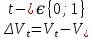 , и, следовательно, принимающий значения только из , и, следовательно, принимающий значения только из 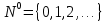 . .Пуассоновским (с некоторой интенсивностью λ > 0) на стохастическом базисе 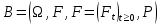 называется точечный процесс называется точечный процесс 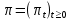 с нулевым начальным значением с нулевым начальным значением 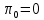 , допускающий разложение Дуба-Мейера: , допускающий разложение Дуба-Мейера: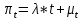 , , где 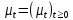 – локально квадратично-интегрируемый мартингал на базисе B с квадратичной характеристикой – локально квадратично-интегрируемый мартингал на базисе B с квадратичной характеристикой 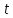 . .Из этого определения вытекают следующие свойства пуассоновского процесса: 1) 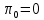 ; ;2) 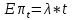 ; ;3) 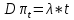 ; ;4) момент остановки 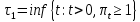 – момент первого скачка процесса π, имеет показательное распределение с функцией распределения – момент первого скачка процесса π, имеет показательное распределение с функцией распределения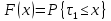 , равной: , равной: 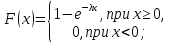 5) случайные величины 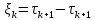 , «отделяющие» моменты k-х скачков процесса π (равные , «отделяющие» моменты k-х скачков процесса π (равные 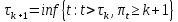 для всех для всех 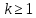 ) имеют показательное распределение с ф. р. ) имеют показательное распределение с ф. р. 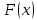 , совпадающей с ф. р. момента , совпадающей с ф. р. момента 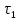 ; ;6) 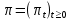 является процессом с независимыми приращениями, и случайные величины является процессом с независимыми приращениями, и случайные величины 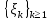 независимы; независимы;7) для каждого момента времени 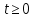 случайная величина случайная величина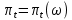 имеет распределение Пуассона: имеет распределение Пуассона: 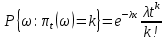 . .Каждая случайная величина полностью определяется своей функцией распределения. Для решения практических задач достаточно знать несколько числовых параметров, которые позволяют представить основные особенности случайной величины в сжатой форме. К таким величинам относятся в первую очередь математическое ожидание и дисперсия. |
