вкр. ВКР Лазарева. Имитационное моделирование систем массового обслуживания с динамическим приоритетом
 Скачать 1.02 Mb. Скачать 1.02 Mb.
|
§2.3. Итерационные формулы для компьютерного моделированияВыведем формулы, необходимые для имитационного моделирования СМО. На стохастическом базисе 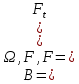 ) из формул (1)-(12) можно получить следующие инфинитезимальные соотношения: ) из формул (1)-(12) можно получить следующие инфинитезимальные соотношения: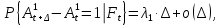 (13) (13)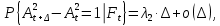 (14) (14)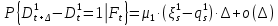 , (15) , (15)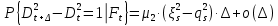 , (16) , (16)Формулы (13)-(16) позволяют, основываясь на понятии геометрической вероятности, провести имитационное моделирование. А именно, введя дискретизацию (шаг по времени) 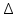 из условия из условия 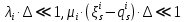 , ,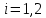 получим следующие итерационные формулы (для вычисления значений процессов в момент времени получим следующие итерационные формулы (для вычисления значений процессов в момент времени 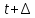 через значения процессов в момент через значения процессов в момент 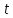 ): ):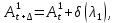 (17) (17)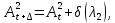 (18) (18)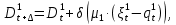 (19) (19)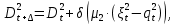 (20) (20)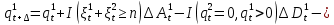 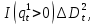 (21) (21)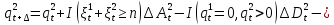 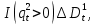 (22) (22)где 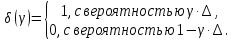 Здесь 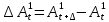 , , 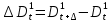 , , 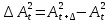 , , 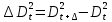 . .Глава 3. Компьютерное моделирование§3.1. Реализация моделиМетоды имитационного компьютерного моделирования систем массового обслуживания являются востребованными, от того, что часто аналитические расчеты являются трудными, а в некоторых случаях невозможными. Для построения имитационных моделей применялся язык программирования высокого уровня С# в среде разработки Visual Studio 2019. Выбор данного языка связан с тем, что он оказался особенно практичным для разработки указанных прежде алгоритмов, ввиду того, что представляется возможным быстрый графический вывод траекторий процессов на экран, а также обладает достаточной оптимизацией для работы. §3.2. Результаты моделированияРезультат моделирования при параметрах T=10, N=1, 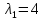 , , 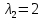 , , 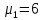 , , 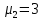 , ∆=0,001, а количество каналов равно 3 приведен на рисунках 3 ,4 и 5. При заданных параметрах наблюдается стабильность в поведении системы, что можно понять по графику среднего количества заявок первого и второго типа в СМО , ∆=0,001, а количество каналов равно 3 приведен на рисунках 3 ,4 и 5. При заданных параметрах наблюдается стабильность в поведении системы, что можно понять по графику среднего количества заявок первого и второго типа в СМО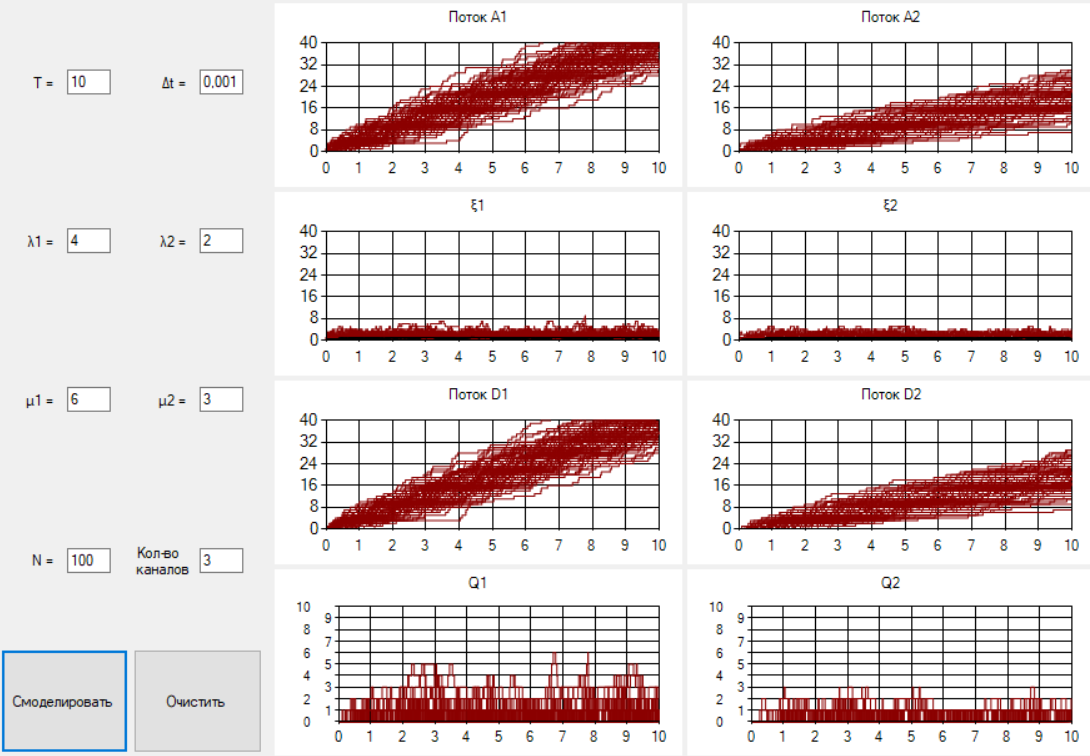 Рис.3. Форма программы с указанными параметрами для 100 траекторий. 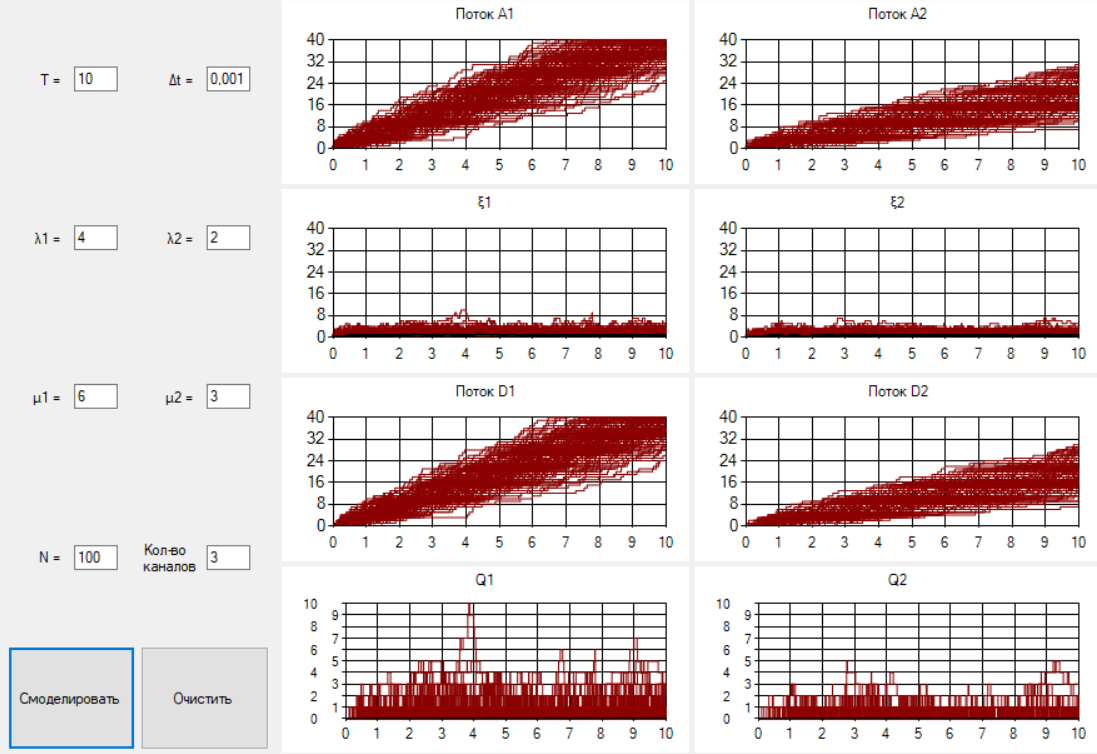 Рис.4. Форма программы с указанными параметрами для 100 траекторий. 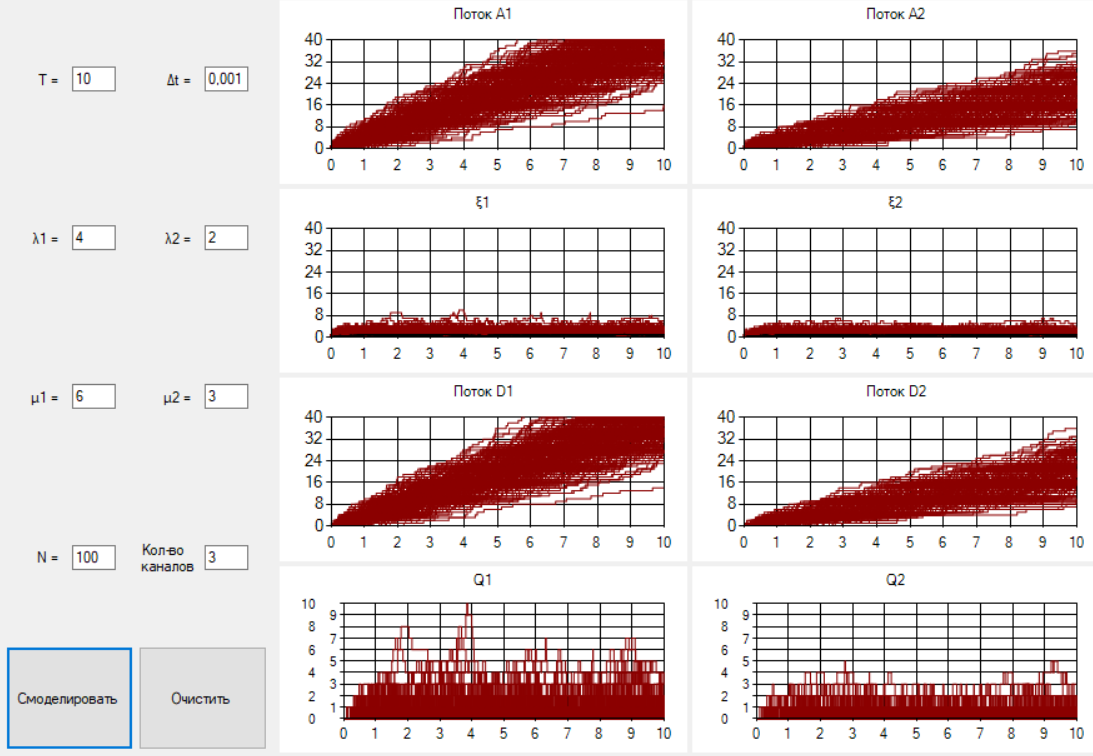 Рис.5. Форма программы с указанными параметрами для 100 траекторий. ЗаключениеВ результате выполнения данной работы была построены математическая и компьютерная модель СМО с динамическим приоритетом. Математическая модель описана в терминах точечных процессов. Также был разработан алгоритм и написана компьютерная программа в среде Visual Studio 2019, реализующая математическую модель. В ходе разработки данной модели были приобретены практические навыки имитационного моделирования СМО в терминах точечных (считающих) процессов. Список литературы Столяров, И.А. Семимартингальная модель СМО с динамическим приоритетом / И.А. Столяров, Ю.Г. Савинов // Прикладная математика и информатика: современные исследования в области естественных и технических наук: материалы III научно-практической всероссийской конференции (школы-семинара) молодых ученых: 24-25 апреля 2017 г. – Тольятти: Издатель Качалин Александр Васильевич, 2017. – стр. 553-557. Гнеденко Б.В. Введение в теорию массового обслуживания / Б.В. Гнеденко, И.Н. Коваленко. – М.:URSS, 2013. – 400 с. Риордан, Д. Вероятностные системы обслуживания / Д. Риордан — Пер. с англ.-М.: Связь, 1966.- 184 с. Алиев Т.И. Основы моделирования дискретных систем. – СПб: СПбГУ ИТМО, 2009. – 363 с. Джейсуол Н. К. Очереди с приоритетами: Пер. с англ. М.: Мир, 1973. 279 с. Бронштейн О. И., Духовный И. М. Модели приоритетного обслуживания в информационно-вычислительных системах. М.: Наука, 1976. 220 с. Лысенкова В. Т. Исследование многолинейных систем массового обслуживания с ограниченным накопителем и приоритетами: Автореф. дис. … канд. техн. наук / Институт проблем передачи информации. М., 1973. Haugen, R.B. Queueing systems with stochastic time out / R.B. Haugen, E. Skogan // IEEE Transactions on Communications. - 1980. - №28. - P.1984-1989. Мова В. В., Пономаренко Л. А., Калиновский А. М. Организация приоритетного обслуживания в АСУ. Киев: Техника, 1977. 160 с. Рыжиков Ю. И. Комплекс программ для расчета систем массового обслуживания повышенной сложности // Программирование. 1978. № 4. С. 87–91 Palm, C. Research on telephone traffic carried by full availability groups / C. Palm // Tele. — 1957. - №1. — P. 107. Саати Т. Л. Элементы теории массового обслуживания и ее приложения: Пер. с англ. М.: Сов. радио, 1965. 510 с. Aguir, S. On the interaction between retrials and sizing of call centers / S. Aguir, F. Karaesmen, O.Z. Aksin, Y. Dallery // Working paper, Кос University, Department of Industrial Engineering. - 2004. - P. 434. Canales, M., Hernández-Solana, Á., Gállego, J.R. et al. Adaptive resource sharing strategies for UMTS multiservice mobiles. Telecommun Syst 28, 151–167 (2005). https://doi.org/10.1007/s11235-004-5014-0 Gerasimenko M., Moltchanov D., Andreev S., Koucheryavy Y., Himayat N., Yeh S.-P., Talwar S. Adaptive resource management strategy in practical multi-radio heterogeneous networks // IEEE Access. Institute of Electrical and Electronics Engineers Inc.. Том Vol 5. 2017. С. 219-235 Antonioli, R.P., Rodrigues, E.B., Maciel, T.F. et al. Adaptive resource allocation framework for user satisfaction maximization in multi-service wireless networks. Telecommun Syst 68, 259–275 (2018). https://doi.org/10.1007/s11235-017-0391-3 Росляков, A.B. Анализ моделей распределенных центров обслуживания вызовов / А.В. Росляков, Н.И. Цыганков // Электросвязь, №8. — 2005.-С. 22-25. Зарипова Э.Р. Математическая модель центра обслуживания вызовов с двумя типами абонентов // Discrete and Continuous Models and Applied Computational Science .- №4.- 2010.- стр.76-82. Ваняшин, С.В. Исследование и разработка моделей мультисервисного центра обслуживания вызовов: дис. ... канд. тех. наук: 05.12.13 / Ваняшин Сергей Владимирович. -М. 2006. - 157 с. Томашевский В. Л. Многоканальные приоритетные системы массового обслуживания: Автореф. дис. … канд. техн. наук. М.: МГУ, 1986. 14 с. Хомоненко А. Д. Вероятностный анализ приоритетного обслуживания с прерываниями в многопроцессорных системах // Автоматика и вычислительная техника. 1990. № 2. С. 55–61. Рыжиков Ю. И. Средние времена ожидания и пребывания в многоканальных приоритетных системах // Информационно-управляющие системы. 2006. № 6. С. 43–49. Рыжиков Ю.И., Уланов А.В. Применение гиперэкспоненциальной аппроксимации в задачах расчета немарковских систем массового обслуживания // Вестник Томского государственного университета. Управление, вычислительная техника и информатика. 2016. № 3(36). C. 60–65. Gail H. R., Hantler S. L., Taylor B. A. Analysis of a non-preemptive priority multiserver queue // Advances in applied prob. 1988. Vol. 20. P. 852. Miller D. R. Steadystate algorithmic analysis of M/M/c two priority queues with heterogeneous rates // Applied probability — computer science: the interface. Vol. 2. Boston: Birkhauser. 1982. P. 207–222. Крылов В.В., Самохвалова С.С., Теория телетрафика и ее приложения. – СПб.: БХВ- Петербург, 2005.-288 с.:ил. Бутов А.А., Савинов Ю.Г. Теория массового обслуживания: Учебно-методическое пособие. -Ульяновск: УлГУ, 2007. Бутов А.А. Оптимальное управление интенсивностью входящего потока многоканальной СМО с роутером при эпизодически наблюдаемой длине очереди на приборах / А.А.Бутов, Л.А. Галимов // Современные проблемы науки и образования. – 2015. – № 2. – С. 758. Бутов А.А., Раводин К.О. Теория случайных процессов: учебно-методическое пособие. – Ульяновск: УлГУ, 2009. Бутов А.А. стохастическая имитационная модель оценки резерва произошедших, но не заявленных страховых убытков в терминах СМО / А.А.Бутов, Л.А. Галимов // Фундаментальные исследования. 2016. № 8-2. С. 234-238. Бутов А.А. Оптимальное управление распределением заявок в многоканальной системе массового обслуживания с входящим пуассоновским потоком поступления заявок и экспоненциальным временем обслуживания / А.А.Бутов, Л.А. Галимов // Естественные и технические науки. 2014. № 9-10 (77). С. 244-247. Савинов Ю.Г., Исмаилова М.В., Рослов М.Э. Траекторные методы моделирования многофазных СМО // Ученые записки УлГУ. Серия: Математика и информационные технологии. 2019. № 1. С. 85-91. Савинов Ю.Г., Тихоненко А.А., Пронин В.И., Щукин А.Н. Семимартингальная модель СМО с произвольным временем ожидания "нетерпеливых" заявок // Ученые записки УлГУ. Серия: Математика и информационные технологии. 2019. № 2. С. 81-88. Савинов Ю.Г., Сафиуллов И.Д., Дуняшина М.С. Модель обслуживания парка оборудования с возможной задержкой в начале ремонта // Ученые записки УлГУ. Сер. Математика и информационные технологии. УлГУ. Электрон. журн. 2020, № 1, с. 103-108. Савинов Ю.Г., Щукин А.Н., Подгорнов М.Д. Математическая модель мультисервисного кол-центра с многоэтапным обслуживанием и дообслуживанием неприоритетных заявок // Ученые записки УлГУ. Серия: Математика и информационные технологии. 2021. № 1. С. 109-117. Савинов Ю.Г., Пронин В. И., Курицин А. Е. Математическая модель центра обслуживания вызовов со случайной задержкой при многоэтапном обслуживании // Ученые записки УлГУ. Сер. Математика и информационные технологии. УлГУ. Электрон. журн. 2021, № 1, с.102-108. Савинов Ю.Г., Рослов М.Э., Куманина Я.А. Стратегия адаптивного разделения ресурсов в мультисервисных сетях// Ученые записки УлГУ. Серия: Математика и информационные технологии. 2020. № 1. С. 95-102. |
