26. Найти двумя способами полином функции. Найти СДНФ, СКНФ.
№
|
f
|
№
|
f
|
№
|
f
|
1
|
1001 0111
|
11
|
0011 1000
|
21
|
0111 1001
|
2
|
0110 1011
|
12
|
0001 0110
|
22
|
0100 1010
|
3
|
1110 0111
|
13
|
1101 1010
|
23
|
0011 1000
|
4
|
0111 1001
|
14
|
0101 1100
|
24
|
1000 0111
|
5
|
1100 0111
|
15
|
1110 1101
|
25
|
0110 0011
|
6
|
1001 0100
|
16
|
0010 1000
|
26
|
0111 1010
|
7
|
1011 0101
|
17
|
1010 1101
|
27
|
1101 0111
|
8
|
1000 0110
|
18
|
0010 0110
|
28
|
0011 1110
|
9
|
1010 0110
|
19
|
1010 0111
|
29
|
1101 1000
|
10
|
0101 1000
|
20
|
0101 1001
|
30
|
0110 0101
|
27. Для функции f(x1, x2, x3, x4) минимизировать ее СДНФ двумя способами.
№
|
f
|
№
|
f
|
№
|
f
|
1
|
1111 0101 0011 1101
|
11
|
0100 1110 1101 1111
|
21
|
1011 1111 0001 1111
|
2
|
1101 1110 1010 1110
|
12
|
1111 1110 0111 1100
|
22
|
1110 1100 1111 1001
|
3
|
0111 0001 1111 1101
|
13
|
1000 1011 1111 1111
|
23
|
1001 1011 1111 1010
|
4
|
1011 1111 1111 1000
|
14
|
1111 1101 1110 0001
|
24
|
1111 1110 0111 0011
|
5
|
1101 0101 1101 1111
|
15
|
1101 0111 1100 1110
|
25
|
1010 1111 0111 0011
|
6
|
1111 1110 1010 0011
|
16
|
1011 1111 1010 1101
|
26
|
1110 0110 1111 1100
|
7
|
111 0010 0111 1110
|
17
|
1001 1101 1010 1111
|
27
|
0111 0111 0101 1011
|
8
|
1100 1110 1111 1011
|
18
|
1110 0110 1111 1100
|
28
|
1101 1111 1110 1010
|
9
|
1100 0110 1111 0111
|
19
|
0011 1011 1010 1111
|
29
|
1111 0011 0111 0111
|
10
|
1011 1111 1110 0010
|
20
|
1111 0110 1110 1110
|
30
|
1110 1110 1010 1101
|
28. Доопределить функции f(x,y,z), g(x,y,z), h(x,y,z) так, чтобы f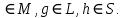 Если построение какой-либо функции невозможно, докажите это. Выясните вопрос о принадлежности построенных функций к классам Если построение какой-либо функции невозможно, докажите это. Выясните вопрос о принадлежности построенных функций к классам 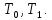
№
|
f
|
g
|
h
|
1
|
-10- 1---
|
-10- -0-0
|
-0-- 11-1
|
2
|
---0 1---
|
0--- 110-
|
11-- 10--
|
3
|
--- 0 -10-
|
---0 0-10
|
-1-- 01-0
|
4
|
-1-- --0-
|
01-0 -1--
|
101- 1---
|
5
|
---0 -01-
|
01-10 ---1
|
--10 --01
|
6
|
--1- -0--
|
-01- -1-1
|
-1-0 -1-0
|
7
|
-0-0 1---
|
1--- 001-
|
-00- 1--1
|
8
|
-1-1 –0-
|
---1 1-01
|
-1-- 10-0
|
9
|
-01- -0--
|
10-1 -0--
|
0--- 101-
|
10
|
---0 1-1-
|
1-01 ---0
|
1--1 -00-
|
11
|
-1-- --01
|
1-1- --00
|
1-10 --1-
|
12
|
0--0 1---
|
--00 1-0-
|
--10 --00
|
13
|
0-1- -0--
|
--10 1-1-
|
-10- 0--1
|
14
|
01-- --0-
|
-00- 1-1-
|
11-1 -0--
|
15
|
---0 1--1
|
0--- 001-
|
-010 ---1
|
16
|
--1- -0-1
|
-10- 0--1
|
-1-- 10-0
|
17
|
-1-- -10-
|
0--1 -0-0
|
00-1 -1--
|
18
|
--00 1---
|
--1- 11-0
|
00-0 -0--
|
19
|
-01- -0--
|
---0 01-0
|
01-- 01--
|
20
|
-1-- 0-0-
|
1--0 -1-1
|
0-10 --0-
|
21
|
---0 1-1-
|
--0- 00-1
|
---1 -010
|
22
|
--11 -0--
|
---1 10-1
|
-1-- 10-0
|
23
|
-10- --0-
|
1--- 110-
|
0--1 -10-
|
24
|
-01- -0--
|
-01- 1--0
|
-1-0 -0-1
|
25
|
-0-0 1---
|
-1-0 1-01
|
1--0 -10-
|
26
|
-1-1 --0-
|
1--0 -01-
|
--01 --11
|
27
|
-0-0 1---
|
01-1 -0--
|
0-00 --0-
|
28
|
--11 -0--
|
-10- 1-0-
|
0--1 -01-
|
29
|
-1-- 011-
|
01-- 1-0-
|
-101 ---0
|
30
|
---0 11--
|
-0-- 101-
|
00-0 -0--
|
29.
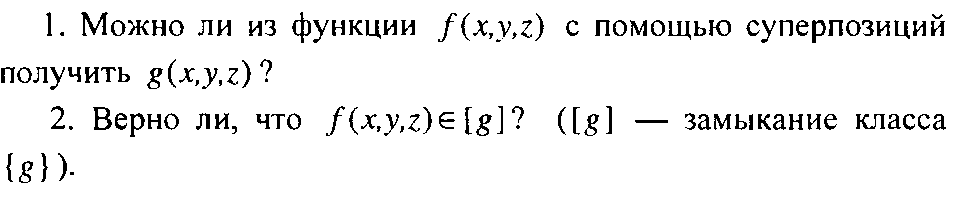 
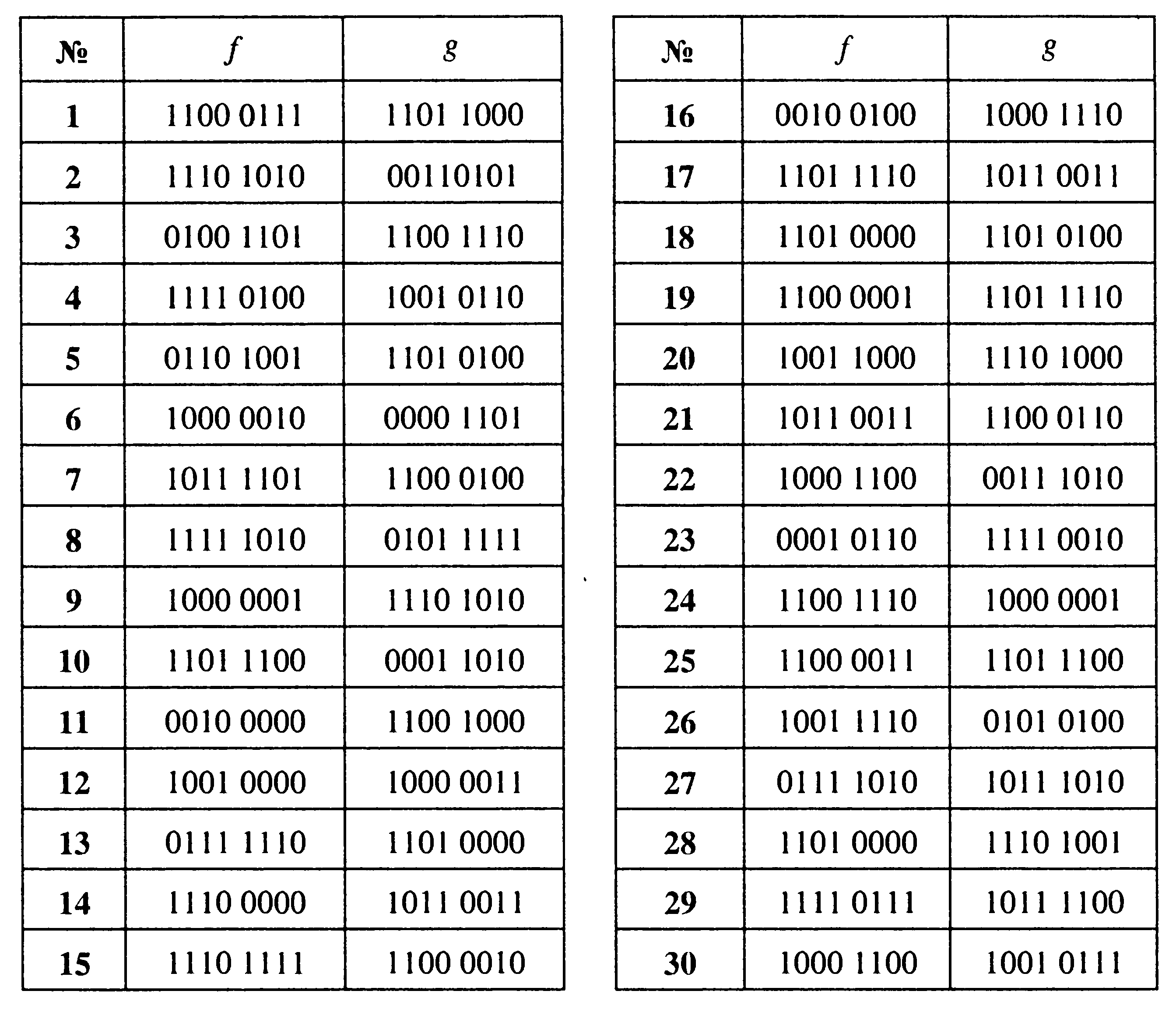
30. Для функций f(x,y,z) и g(x,y,z) выяснить вопрос об их принадлежности к классам T0, T1, L, S,M. В случае, если некоторая функция представляет из себя функционально полный класс, выразить с ее помощью суперпозиций константы 0, 1, отрицание и конъюнкцию xy.
31. Определить значение истинности высказывания.
№
|
Высказывание
|
|
 , где , где 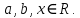
|
|
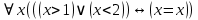 , где , где 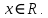
|
|
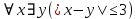 , где , где 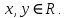
|
|
 , где , где 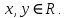
|
|
 , где , где 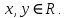
|
|
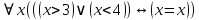 , где , где 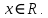
|
|
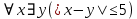 , где , где 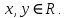
|
|
 , где , где 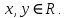
|
|
 , где , где 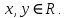
|
|
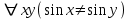 , где , где 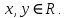
|
|
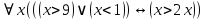 , где , где 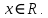
|
|
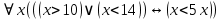 , где , где 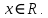
|
|
 , где , где 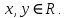
|
|
 , где , где 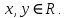
|
|
 , где , где 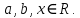
|
|
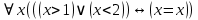 , где , где 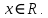
|
|
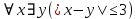 , где , где 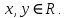
|
|
 , где , где 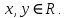
|
|
 , где , где 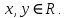
|
|
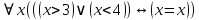 , где , где 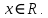
|
|
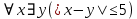 , где , где 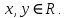
|
|
 , где , где 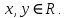
|
|
 , где , где 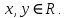
|
|
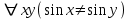 , где , где 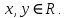
|
|
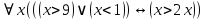 , где , где 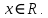
|
|
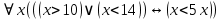 , где , где 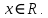
|
|
 , где , где 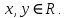
|
|
 , где , где 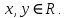
|
|
 , где , где 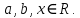
|
|
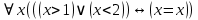 , где , где 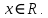
| |
 Скачать 1.1 Mb.
Скачать 1.1 Mb.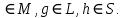 Если построение какой-либо функции невозможно, докажите это. Выясните вопрос о принадлежности построенных функций к классам
Если построение какой-либо функции невозможно, докажите это. Выясните вопрос о принадлежности построенных функций к классам 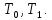
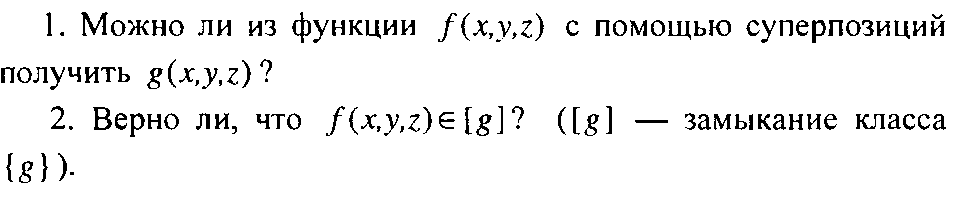



 , где
, где 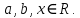
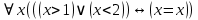 , где
, где 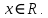
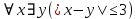 , где
, где 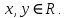
 , где
, где  , где
, где 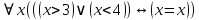 , где
, где 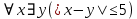 , где
, где  , где
, где  , где
, где 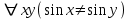 , где
, где 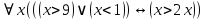 , где
, где 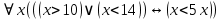 , где
, где  , где
, где  , где
, где