Философиялык негздер. 1силлабус механика 2020-2021 СКАНЕР. Информация о дисциплине
 Скачать 1.43 Mb. Скачать 1.43 Mb.
|
|
Inertia forces at accelerated translational motion of the reference system. Let on a trolley to the tripod on thread is suspended a ball of mass m (Fig. 23). While the truck is at rest or moves uniformly by a straight line, the thread, holding the ball, takes a vertical position and the force of gravity P is balanced by the reaction force of thread T. 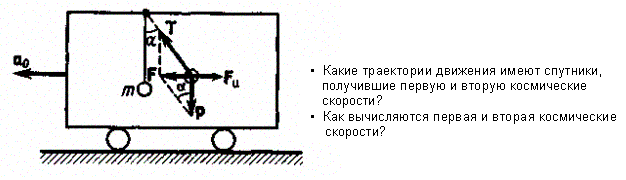 Figure 23 If the truck lead into linear motion with acceleration, then the thread starts to deviate from the vertical back to the angle until the resultant force F=P + T does not provide the acceleration of the ball equal. Thus, the resultant force F is directed toward the acceleration of trolley and for steady motion of the ball (a ball is now moving along the trolley acceleration а0) equal F = mgtg = ma0, from which 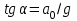 i. e. the angle of thread deviation from the vertical is greater, the greater the acceleration of the trolley. Regarding the frame of reference associated with rapidly moving trolley, the ball is at rest, it is possible, if the force F is balanced by an equal and opposite by direction force, which is the force of inertia, because on ball it does not act any other force. So, 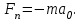 (5.8) (5.8)2. The inertial forces acting on the body at rest in the rotating frame. Let the disc rotates uniformly with angular velocity ( —const) around the vertical axis passing through its center. On disk, at different distances from the axis of rotation, set the pendulums (on threads are suspended balls of mass m). At rotating of pendulums with disk the balls deviate from the vertical to some angle (Fig. 24). 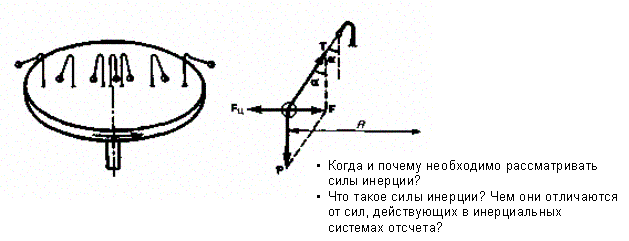 Figure 24 In an inertial frame of reference, such as those associated with the location where the disk is installed, the ball rotates uniformly in a circle of radius R (the distance from the rotating center of the ball to the rotation axis). Consequently, on it the force is equal F = m2R and directed perpendicular to the axis of rotation of the disk. It is the resultant of gravity P and the thread tension force Т: F=P + T. When the ball movement have been stable, the F = mgtg =m2R, and 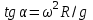 i.e. the pendulums thread deviation angles are greater, the greater the distance R from the center of the ball to the disc rotation axis and the greater the angular velocity . Regarding the frame of reference associated with the rotating disc, the ball is at rest, which is possible if the force F is balanced by an equal and opposite by direction force Fc, which is the force of inertia, because no other forces act on the ball. Force Fc is called centrifugal inertial force and directed along the horizontal axis of rotation of the disk and is equal to 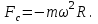 (5.9) (5.9)3. The forces of inertia, acting on the moving body in rotating system. Let the ball of mass m moves with constant velocity v' uniformly along the radius of the rotating disk (v' = const, = const, v'). If the disk does not rotate, the ball directed along the radius, moves along a radial line and enters the point A, if the disc is set in rotation in the direction indicated by the arrow, the ball rolls along the curve OB (Fig. 31 a), and its speed v' relative to the disk changes its direction. This is possible only if the ball experiences a force perpendicular to the velocity v'. 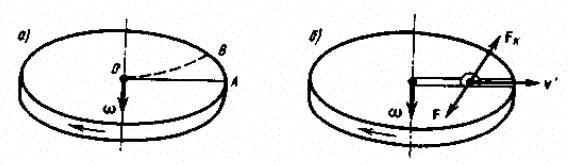 Figure 25 In order to get the ball rolling on a rotating disk along the radius, use a rod hardly fortified along the radius of a disk on which the ball moves without friction uniformly and in a straight line with a velocity v' (Fig. 25b). At the deviation of the ball the rod acts on it with some force F. With respect to the disc (rotating reference frame), the ball moves uniformly in a straight line, which can be explained by the fact that the force F is balanced applied to the ball inertia force FK, perpendicular to the velocity v'. This force is called the Coriolis force of inertia. It can be shown that the Coriolis force * 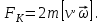 (5.10) (5.10)Vector FK is perpendicular to the velocity vector v body and the angular velocity of reference system in accordance with the right-handed screw rule. The Coriolis force acts only on the bodies moving relative to a rotating frame of reference, for example, with respect to the Earth. Therefore, the number of observed phenomena in the world is due to the action of these forces. So, if the body moves in the northern hemisphere to the north (Fig. 26), then acting on it, the Coriolis force, as it follows from (5.10), will be directed to the right relative to the direction of motion, i.e. the body deviates to the east . If the body moves to the south, the Coriolis force acts to the right also, if we see in the direction of motion, i.e. body deviates to the west. Therefore, in the northern hemisphere there is a stronger cleaning the right river banks; right railway tracks motion wear out faster than the left, etc. Similarly, we can show that in the southern hemisphere the Coriolis force acting on the moving bodies, will be directed to the left in relation to the movement. Due to the Coriolis force, the bodies falling on the surface of the Earth deviate to the east (at the latitude of 60, this deviation must be 1 cm when dropped from a height of 100 m). With the Coriolis force is associated the behavior of Foucault pendulum which was at one time one of the proofs of the Earth's rotation. If this force is not there, the plane of oscillation of the oscillating pendulum near the Earth's surface would remain unchanged (relative to the Earth). The action of the Coriolis force rotates the oscillation plane around the vertical direction.  Figure 26 Expanding content Fin in formula ( 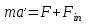 ), we obtain the fundamental law of dynamics for the non-inertial reference systems: ), we obtain the fundamental law of dynamics for the non-inertial reference systems: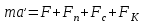 where the forces of inertia are given by (5.8) – (5.10). Вопросы для закрепления** - Give The examples of noninertial reference frames -What is the Inertia force Литература: 1. Zhanturina N., Myasnikova. Fundamentals of Mechanics. – Aktobe, 2018. – 105 p. 2. Yar-Mukhamedova G.Sh., Shunkeyev K.Sh., Zhanturina N.N. Mechanics. – Almaty: Ka-zakh University. -132 p. 3. S. Thornton, A. Rex. Modern physics. –University of Virginia. 2013. – 613 p. 4. I.E. Irodov. Problems in general physics. – Moscow, 1981. – 385 p. 5. A. Beiser. Applied physics. – USA, 2003. – 138 p. DOI: 10.1036/0071425853 6. S. Holzner. Physics for dummies. – Hoboken, 2006. – 368 p. 9.1.12 Тема: 12. Galileo transformations. Mechanical principle of relativity Количество часов:1 Основные вопросы/план темы: 1. Transformations of velocities 2. Galileo transformations 3. Lorentz transformations Тезисы лекции* Galileo noted that any mechanical experiments carried out in the inertial frame of reference, it is impossible to establish whether it is at rest or moves uni-formly by a straight line. For example, sitting in the cabin of the ship moving uni-formly straight forward, we can not determine if the ship is resting or moving uniformly and bu straight line, not looking out the window. In classical mechanics, the mechanical principle of relativity is valid (the principle of Galilean relativity): laws of dynamics are the same in all inertial ref-erence systems. The basis of the special theory of relativity, Einstein's postulates are for-mulated them in 1905. 1. The principle of relativity: no experiments (mechanical, electrical, opti-cal), carried out within a given inertial reference system, make it impossible to de-tect whether the system is at rest or moves uniformly in a straight line; all laws of nature are invariant with respect to the transition from one inertial reference sys-tem to another. 2. The principle of invariance of the speed of light: the speed of light in vac-uum does not depend on the speed of movement of the light source or the ob-server, and the same in all inertial reference systems. Вопросы для закрепления** - what is the Galileo transformations? - Give definition of Mechanical principle of relativity Литература: 1. Zhanturina N., Myasnikova. Fundamentals of Mechanics. – Aktobe, 2018. – 105 p. 2. Yar-Mukhamedova G.Sh., Shunkeyev K.Sh., Zhanturina N.N. Mechanics. – Almaty: Ka-zakh University. -132 p. 3. S. Thornton, A. Rex. Modern physics. –University of Virginia. 2013. – 613 p. 4. I.E. Irodov. Problems in general physics. – Moscow, 1981. – 385 p. 5. A. Beiser. Applied physics. – USA, 2003. – 138 p. DOI: 10.1036/0071425853 6. S. Holzner. Physics for dummies. – Hoboken, 2006. – 368 p. 9.1.13 Тема: 13. Main law of relativistic dynamics of a material point Количество чаов:1 Основные вопросы/план темы: 1. The relationship between mass and energy 2. Main law of dynamics Тезисы лекции* From Einstein's principle of relativity, asserting the invariance of the laws of nature in the transition from one inertial reference system to another, it should be a condition of invariance of physical laws under the Lorentz transformation equa-tions. Newton's fundamental law of dynamics Mass of moving particles does not depend on their velocities: 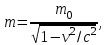 (7.16) (7.16)where m0is the rest mass of the particle, i.e., the mass measured in the inertial reference frame with respect to which the particle is at rest; c is the velocity of light in vacuum; m - mass of the particle in the reference frame, with respect to which it moves at a speed v. Consequently, the mass of the same particle is different in different inertial frames. From Einstein's principle of relativity (see § 7.2), asserting the invariance of the laws of nature in the transition from one inertial reference system to another, it should be a condition of invariance of physical laws under the Lorentz transformation equations. Newton's fundamental law of dynamics 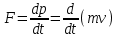 is also invariant with respect to Lorentz transformations, if the time derivative of the relativistic momentum is right. The fundamental law of the relativistic dynamics of a material point is 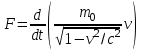 (7.17) (7.17)or 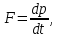 where 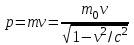 – relativistic momentum of a material point. Let’s find the kinetic energy of relativistic particle. Later (§ 3.2) it was shown, that the change in kinetic energy of a material point on the elementary displacement is equal to the work of force on this displacement: 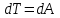 or or 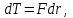 (7.18) (7.18)Taking into account that dr=vdt, and put in (7.18) the expression (7.17), we obtain 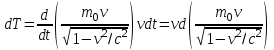 Transforming this equation taking into account that, vdv=d and formulas (7.18), we obtain 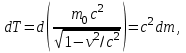 (7.19) (7.19)i.е. the change in kinetic energy of a particle is directly proportional to the change in mass. Вопросы для закрепления** - what is Main law of dynamics? - Describe the The relationship between mass and energy Литература: 1. Zhanturina N., Myasnikova. Fundamentals of Mechanics. – Aktobe, 2018. – 105 p. 2. Yar-Mukhamedova G.Sh., Shunkeyev K.Sh., Zhanturina N.N. Mechanics. – Almaty: Ka-zakh University. -132 p. 3. S. Thornton, A. Rex. Modern physics. –University of Virginia. 2013. – 613 p. 4. I.E. Irodov. Problems in general physics. – Moscow, 1981. – 385 p. 5. A. Beiser. Applied physics. – USA, 2003. – 138 p. DOI: 10.1036/0071425853 6. S. Holzner. Physics for dummies. – Hoboken, 2006. – 368 p. 9.1.14 Тема: 14. Pressure in liquid and gas. The equation of continuity Количество часов:1 Основные вопросы/план темы: 1. Pressure in liquid and gas 2. Continuity equation Тезисы лекции* The physical quantity defined by the normal force exerted by a fluid per unit area is called pressure p of fluid: 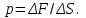 The unit of pressure - pascal (Pa): 1 Pa is equal to pressure generated by force of 1 N, evenly distributed over normal to its surface of 1 m2 (1 Pa = 1 N/ m2). The pressure at equilibrium of fluids (gases) obeys Pascal law: pressure in a fluid at rest anywhere equally in all directions, and pressure is the same transmitted the whole volume occupied by the fluid at rest. Let’s consider the effect of the weight of the fluid on the pressure distribution inside the stationary incompressible fluid. At equilibrium, the pressure by horizontal is always the same, otherwise there were no equilibrium. Therefore, the free surface of a liquid at rest is always horizontal away from the vessel walls. If the fluid is incompressible, its density does not depend on pressure. Then, at the cross-section S of the liquid, its height h and density the weight P=gSh, and the pressure on the lower base 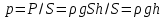 (6.1) (6.1)i. e. the pressure varies linearly with altitude. Pressure gh is called hydrostatic pressure. According to formula (6.1), the force of pressure on the lower layers of the liquid is greater than the upper, so on body immersed in a fluid, acts the force, which is determined by the law of Archimedes: on a body immersed in a fluid (gas), on the part of the liquid acts the buoyant force directed upward and equal to the weight of the displaced fluid by body (gas): 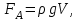 where — density of the fluid, V— the volume of the body. Fluid motion is called the flow, and the collection of particles of moving fluid - flux. Part of the liquid, limited by current lines, is called the current tube. The flow of fluid is called steady (or stationary), if the shape and location of the streamlines and the velocity values at each point does not change with time. Вопросы для закрепления** - Give the definition of pressure - Give the definition of Pascal Law Литература: 1. Zhanturina N., Myasnikova. Fundamentals of Mechanics. – Aktobe, 2018. – 105 p. 2. Yar-Mukhamedova G.Sh., Shunkeyev K.Sh., Zhanturina N.N. Mechanics. – Almaty: Ka-zakh University. -132 p. 3. S. Thornton, A. Rex. Modern physics. –University of Virginia. 2013. – 613 p. 4. I.E. Irodov. Problems in general physics. – Moscow, 1981. – 385 p. 5. A. Beiser. Applied physics. – USA, 2003. – 138 p. DOI: 10.1036/0071425853 6. S. Holzner. Physics for dummies. – Hoboken, 2006. – 368 p. 9.1.15 Тема: 15. Bernoillies equation Количество часов:1 Основные вопросы/план темы: 1. The derivation of Bernouliies equation 2. Static pressure 3. Hydrostatic pressure Тезисы лекции* The value of p in the formula (6.8) is called the static pressure (liquid pres-sure on the surface of the body with it), the value of pv2/2 - dynamic pressure. The Bernoulli equation is used to find the rate of liquid outflow through the gup in the wall or bottom of the vessel. Consider a cylindrical container with a liquid, in side wall of which the at a certain depth or the same liquid level there is a small hole According to the law of conservation of energy, the total energy change E2-E1 of an ideal incompressible liquid should be equal to the work of external forces on the movement of the mass m of liquid: 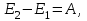 (6.3) (6.3)where E1 and E2 – total energy of fluid with mass m in sections S1 and S2respectively On the other hand, A – is the work done by motion all the liquid contained between sections S1 and S2, for the considered small time interval t. For the transfer of mass m from S1 to S2 fluid must move a distance l1 = v1t and from S2 to S2 – a distance l2=v2t. Note that l1 and l2are so small that all points of the volumes, shaded in Fig. 28 have constant values of velocity v, pressure p and height h. Consequently, 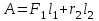 (6.4) (6.4)where F1 = p1S1and F2 = -p2S2 (negative, as directed in the direction opposite to the fluid flow, Fig. 28). Full energy will be formed from the kinetic and potential energies E1 and E2 of the mass m of liquid: 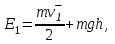 (6.5) (6.5)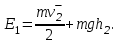 (6.6) (6.6)Substituting (6.5) and (6.6) to (6.3) and equating (6.3) and (6.4), we obtain 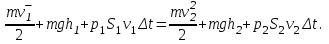 (6.7) (6.7)According to the continuity equation for an incompressible fluid ( 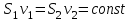 ), the volume occupied by the liquid remains constant, i.e. ), the volume occupied by the liquid remains constant, i.e.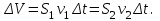 Dividing the expression (6.7) on V, we obtain 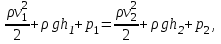 here - density of the liquid. But as the section chosen arbitrarily, then we can write 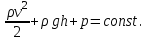 (6.8) (6.8)The expression (6.8) is derived by the Swiss physicist Daniel Bernoulli (1700-1782; published in 1738), and is called the equation Bernoulli. The value of p in the formula (6.8) is called the static pressure (liquid pressure on the surface of the body with it), the value of pv2/2 - dynamic pressure. Вопросы для закрепления** - what is the static pressure? - Give the definition of Bernoillies equation Литература: 1. Zhanturina N., Myasnikova. Fundamentals of Mechanics. – Aktobe, 2018. – 105 p. 2. Yar-Mukhamedova G.Sh., Shunkeyev K.Sh., Zhanturina N.N. Mechanics. – Almaty: Ka-zakh University. -132 p. 3. S. Thornton, A. Rex. Modern physics. –University of Virginia. 2013. – 613 p. 4. I.E. Irodov. Problems in general physics. – Moscow, 1981. – 385 p. 5. A. Beiser. Applied physics. – USA, 2003. – 138 p. DOI: 10.1036/0071425853 6. S. Holzner. Physics for dummies. – Hoboken, 2006. – 368 p. |
