Философиялык негздер. 1силлабус механика 2020-2021 СКАНЕР. Информация о дисциплине
 Скачать 1.43 Mb. Скачать 1.43 Mb.
|
|
9.4 Самостоятельная работа студента с преподавателем (СРСП) 9.4.1. Newton's ideas about the properties of space and time Методические указания. .In the self-work must be considered some definitions, main laws and their derivations. At the performing the task it is recommended to consider more than 3 references and compared some definitions. Литература: 1. S. Thornton, A. Rex. Modern physics. –University of Virginia. 2013. – 613 p. 2. I.E. Irodov. Problems in general physics. – Moscow, 1981. – 385 p. 3. A. Beiser. Applied physics. – USA, 2003. – 138 p. DOI: 10.1036/0071425853 4. S. Holzner. Physics for dummies. – Hoboken, 2006. – 368 p. 5. Гершензон Е.М., Малов Н.Н. Курс общей физики. Механика. М, 2000 6. Бордовский Г.А., Бурсиан Э.В. Общая физика. Курс лекций, т. 1. М, 2001 7. Детлаф А.А., Яворский Б.М. Курс физики. М, 2000 8. Бурштейн А.И. Молекулярная физика. М, 1986 9.4.2. Types of equilibrium. Center of gravity Методические указания. In the self-work must be considered some definitions, main laws and their derivations. At the performing the task it is recommended to consider more than 3 references and compared some definitions. Литература:  9.4.3. Fluid friction. Motion of bodies in a viscous medium Методические указания. To get acquainted with the general methods of studying the basic physical phenomena; mastering the fundamental concepts, laws and theories of modern physics. It is necessary to learn the basics of independent activity in studying the course. Литература:  9.4.4. The laws of dry friction Методические указания. In the self work must be the examples of the phenomena in nature. Also have to be included diagrams, schemes, plots. Must be considered some problems. The question of task must be done by the plan and the parts of is connected. Литература:  9.4.5.-9.4.7. Hooke's law for various deformations: one-sided stretching (compression), all-round compression, shear, torsion Методические указания. To get acquainted with the general methods of studying the basic physical phenomena; mastering the fundamental concepts, laws and theories of modern physics. It is necessary to learn the basics of independent activity in studying the course. Литература:  9.4.8. Plan The law of universal gravitation. Gravity and weight. Weightlessness Методические указания. In the self-work must be considered some definitions, main laws and their derivations. At the performing the task it is recommended to consider more than 3 references and compared some definitions. Литература:  9.4.9. The manifestation of inertia forces on the Earth. Foucault's pendulum. Plan Методические указания. To get acquainted with the general methods of studying the basic physical phenomena; mastering the fundamental concepts, laws and theories of modern physics. It is necessary to learn the basics of independent activity in studying the course. Литература:  9.4.10. Voice and hearing aids. Objective and subjective characteristics of sound Методические указания. In the self work must be the examples of the phenomena in nature. Also have to be included diagrams, schemes, plots. Must be considered some problems. The question of task must be done by the plan and the parts of is connected. Литература:  9.4.11. Pressure Методические указания. In the self-work must be considered some definitions, main laws and their derivations. At the performing the task it is recommended to consider more than 3 references and compared some definitions. Литература:  9.4.12. Laminar and turbulent flow regimes of liquids. The Stokes formula. Reynolds number Методические указания. To get acquainted with the general methods of studying the basic physical phenomena; mastering the fundamental concepts, laws and theories of modern physics. It is necessary to learn the basics of independent activity in studying the course. Литература:  9.4.13. Damped and forced oscillations. Resonance. Self-oscillations Методические указания. To get acquainted with the general methods of studying the basic physical phenomena; mastering the fundamental concepts, laws and theories of modern physics. It is necessary to learn the basics of independent activity in studying the course. Литература:  9.4.14. Addition of oscillations Методические указания. To get acquainted with the general methods of studying the basic physical phenomena; mastering the fundamental concepts, laws and theories of modern physics. It is necessary to learn the basics of independent activity in studying the course. Литература:  9.4.15. The main characteristics of the wave. Equation of a wave. Formation of standing waves Методические указания. In the self work must be the examples of the phenomena in nature. Also have to be included diagrams, schemes, plots. Must be considered some problems. The question of task must be done by the plan and the parts of is connected. Литература:  9.4.16. Sound waves. Propagation of sound in the atmosphere. The Doppler effect. Sources of sound. Методические указания. In the self-work must be considered some definitions, main laws and their derivations. At the performing the task it is recommended to consider more than 3 references and compared some definitions. Литература:  9.5 Самостоятельная работа студента (СРС) 9.5.1. Information about vectors. Hodograph method Методические указания. In the self-work must be considered some definitions, main laws and their derivations. Литература:  9.5.2. The relationship between linear and angular quantities Методические указания. In the self-work must be considered some definitions, main laws and their derivations. Литература:  9.5.3. Movement of the body, cast at an angle to the horizon. The equilibrium conditions of the mechanical system Методические указания. In the self-work must be considered some definitions, main laws and their derivations. Литература:  9.5.4. Application of Newton's laws. The nature of forces Методические указания. In the self-work must be considered some definitions, main laws and their derivations. Литература:  9.5.5. Application of conservation laws Методические указания. In the self-work must be considered some definitions, main laws and their derivations. Литература:  9.5.6. Movement of a body in a noninertial reference frame Методические указания. In the self-work must be considered some definitions, main laws and their derivations. Литература:  9.5.7. The effect of centrifugal force on the acceleration of gravity. Foucault's pendulum Методические указания. In the self-work must be considered some definitions, main laws and their derivations. Литература:  9.5.8. Motion of a body with a variable mass. The manifestation of frictional forces Методические указания. In the self-work must be considered some definitions, main laws and their derivations. Литература:  9.5.9. Application of the gyroscopic effect in physics and engineering. Gyroscopes Методические указания. In the self-work must be considered some definitions, main laws and their derivations. Литература:  9.5.10. Application of the laws of the dynamics of a rigid body. Методические указания. In the self-work must be considered some definitions, main laws and their derivations. Литература:  9.5.11. The effect of centrifugal force on the acceleration of gravity. Foucault's pendulum Методические указания. In the self-work must be considered some definitions, main laws and their derivations. Литература:  9.5.12. Motion of a body with a variable mass. The manifestation of frictional forces Методические указания. In the self-work must be considered some definitions, main laws and their derivations. Литература:  9.5.13. Levers. A couple of forces. Rolling Методические указания. In the self-work must be considered some definitions, main laws and their derivations. Литература:  9.5.14 The principle of equivalence of gravitational forces and inertia forces. Inert and gravitational mass Методические указания. In the self-work must be considered some definitions, main laws and their derivations. Литература:  9.5.15. Dependence of gravity acceleration on latitude Методические указания. In the self-work must be considered some definitions, main laws and their derivations. Литература 9.5.16. Gravitational constant. The Cavendish Experience Методические указания. In the self-work must be considered some definitions, main laws and their derivations. Литература:  9.5.17. Kepler's Laws. Artificial satellites. Supersonic speeds Методические указания. In the self-work must be considered some definitions, main laws and their derivations. Литература:  9.5.18. The Michelson Experiment Методические указания. In the self-work must be considered some definitions, main laws and their derivations. Литература:  9.5.19. Friction in a moving fluid. Pitot tube. Application of the law of conservation of momentum for the motion of a liquid Методические указания. In the self-work must be considered some definitions, main laws and their derivations. Литература:  9.5.20. Graphical representation of harmonic oscillations. Logarithmic decrement decrement. Parametric resonance Методические указания. In the self-work must be considered some definitions, main laws and their derivations. Литература:  9.5.21. Oscillations in nonlinear systems. String vibrations Методические указания. In the self-work must be considered some definitions, main laws and their derivations. Литература:  9.5.22. Sources and receivers of sound. Ultrasounds. Limits of applicability of classical Методические указания. In the self-work must be considered some definitions, main laws and their derivations. Литература:  10. ЗАДАНИЯ И ВОПРОСЫ РУБЕЖНОГО И ПРОМЕЖУТОЧНОГО КОНТРОЛЯ Motion along a straight line 1. A particle moves along the x axis from xi to xf. Of the following values of the initial and final coordinates, which results in the displacement with the largest magnitude? A. xi =4m, xf =6m D. xi =4m, xf = −2m B. xi = −4m, xf = −8m E. xi = −4m, xf =4m C. xi = −4m, xf =2m 2. The average speed of a moving object during a given interval of time is always: A. the magnitude of its average velocity over the interval B. the distance covered during the time interval divided by the time interval C. one-half its speed at the end of the interval D. its acceleration multiplied by the time interval E. one-half its acceleration multiplied by the time interval. 3. Each of four particles move along an x axis. Their coordinates (in meters) as functions of time (in seconds) are given by particle 1:x(t) = 3.5−2.7t3 particle 3:x(t) = 3.5+2.7t2 particle 2:x(t) = 3.5+2.7t3 particle 4:x(t) = 3.5−3.4t−2.7t2 Which of these particles have constant acceleration? A. All four C. Only 2 and 3 E. None of them B. Only 1 and 2 D. Only 3 and 4 4. Each of four particles move along an x axis. Their coordinates (in meters) as functions of time (in seconds) are given by particle 1:x(t) = 3.5−2.7t3 particle 3:x(t) = 3.5+2.7t2 particle 2:x(t) = 3.5+2.7t3 particle 4:x(t) = 3.5−3.4t−2.7t2 Which of these particles is speeding up fort >0? A. All four D. Only 2, 3, and 4 B. Only 1 E. None of them C. Only 2 and 3 5. A ball is in free fall. Upward is taken to be the positive direction. The displacement of the ball during a short time interval is: A. positive during both ascent and descent B. negative during both ascent and descent C. negative during ascent and positive during descent D. positive during ascent and negative during descent E. none of the above 6. Which of the following five acceleration versus time graphs is correct for an object moving in a straight line at a constant velocity of 20 m/s? 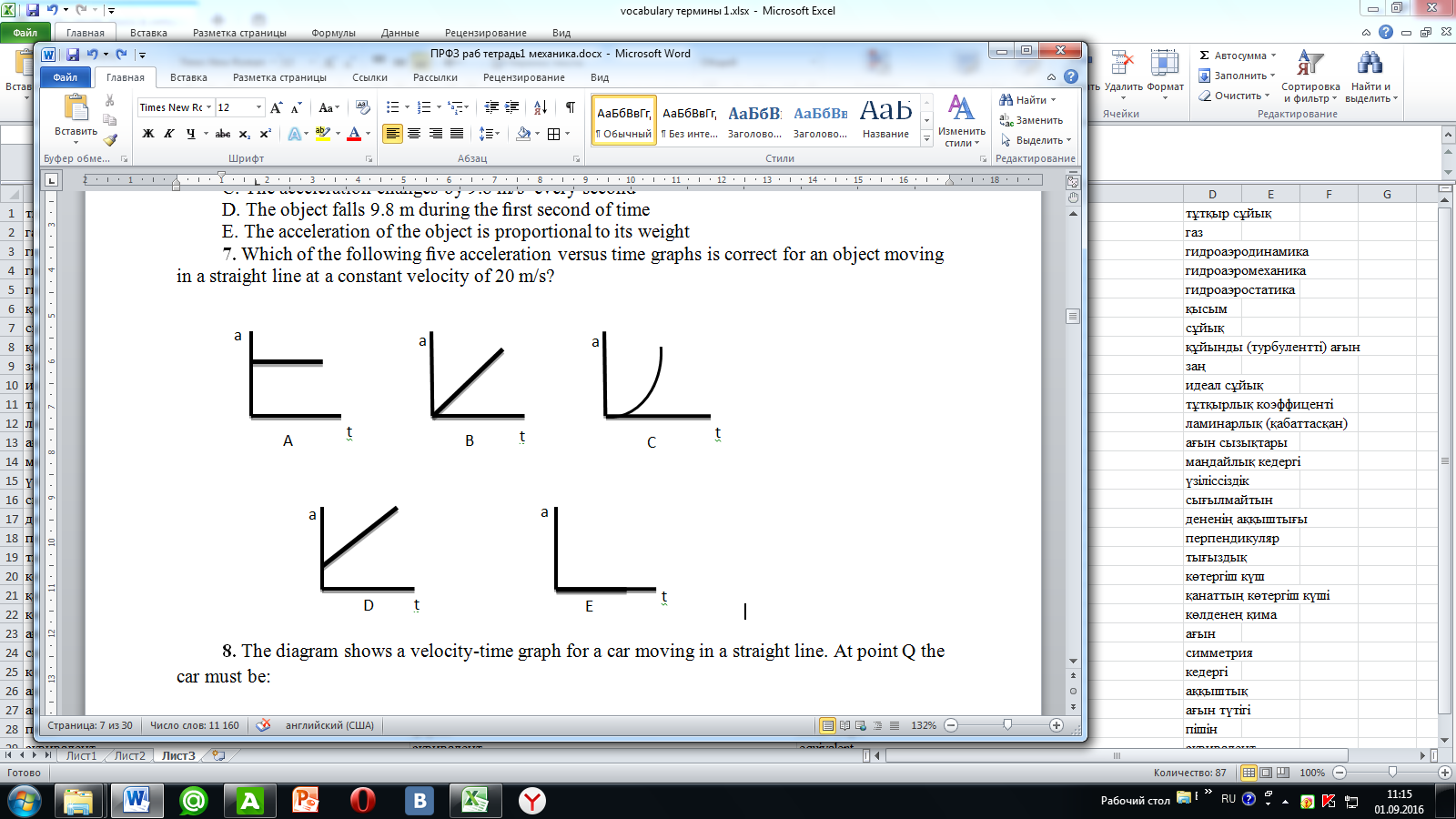   7. Which one of the following statements is correct for an object released from rest? A. The average velocity during the first second of time is 4.9 m/s B. During each second the object falls 9.8 m C. The acceleration changes by 9.8 m/s2 every second D. The object falls 9.8 m during the first second of time E. The acceleration of the object is proportional to its weight 8. The diagram shows a velocity-time graph for a car moving in a straight line. At point Q the car must be:
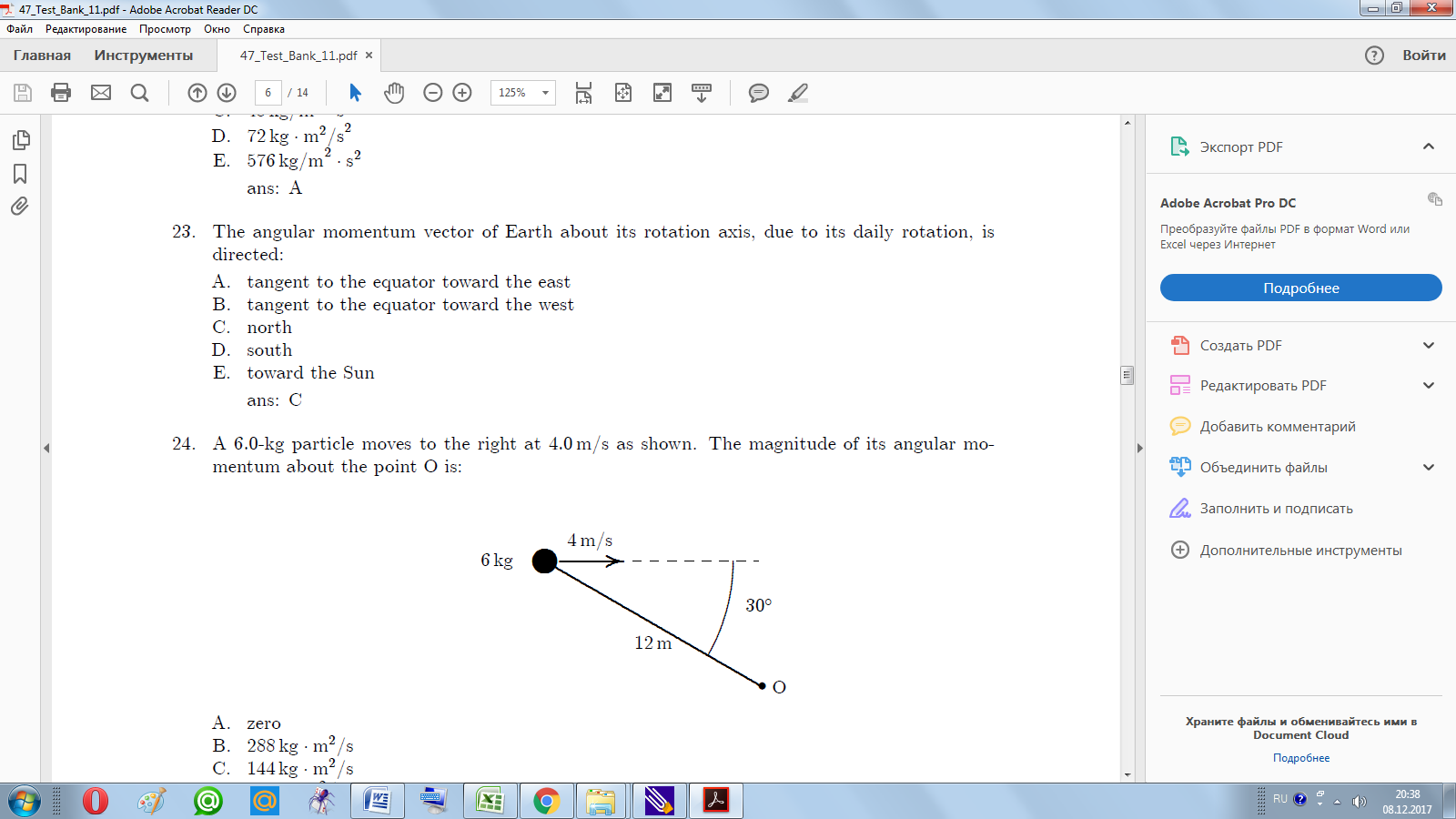
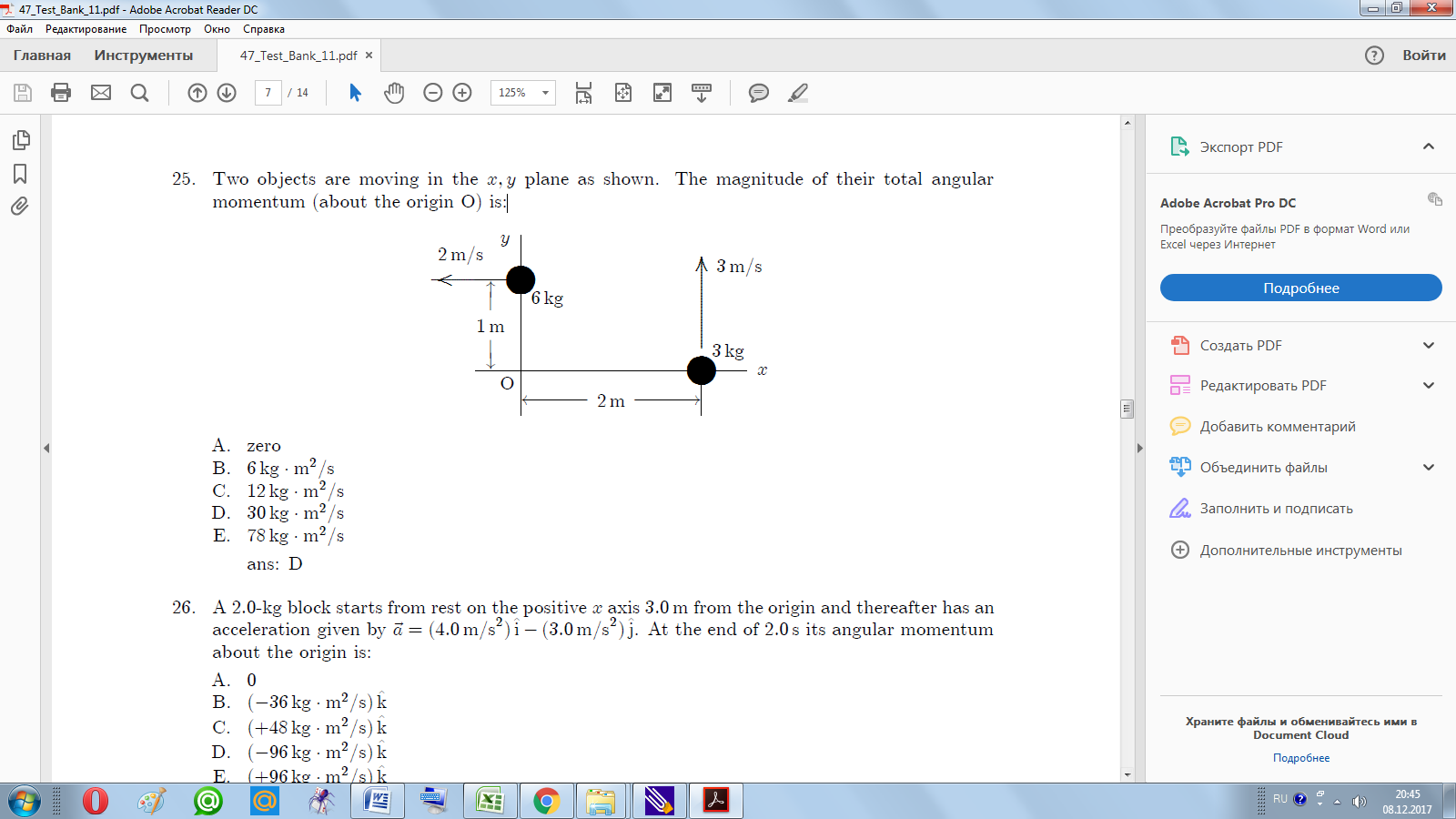
9. The area under a velocity-time graph represents: A. acceleration D. change in velocity B. change in acceleration E. displacement C. speed 10. Displacement can be obtained from: A. the slope of an acceleration-time graph B. the slope of a velocity-time graph C. the area under an acceleration-time graph D. the area under a velocity-time graph E. the slope of an acceleration-time graph Motion in two and three dimensions 1. A bullet shot horizontally from a gun: A. strikes the ground much later than one dropped vertically from the same point at the same instant. B. never strikes the ground C. strikes the ground at approximately the same time as one dropped vertically from the same point at the same instant. D. travels in a straight line E. strikes the ground much sooner than one dropped from the same point at the same instant 2. A jet plane in straight horizontal flight passes over your head. When it is directly above you, the sound seems to come from a point behind the plane in a direction 300 from the vertical. The speed of the plane is: A. the same as the speed of sound D. 0.866 times the speed of sound B. half the speed of sound E. twice the speed of sound C. three-fifths the speed of sound 3. The velocity of a projectile equals its initial velocity added to: A. a constant horizontal velocity B. a constant vertical velocity C. a constantly increasing horizontal velocity D. a constantly increasing downward velocity E. a constant velocity directed at the target 4. Two bodies are falling with negligible air resistance, side by side, above a horizontal plane. If one of the bodies is given an additional horizontal acceleration during its descent, it: A. strikes the plane at the same time as the other body B. strikes the plane earlier than the other body C. has the vertical component of its velocity altered D. has the vertical component of its acceleration altered E. follows a straight line path along the resultant acceleration vector 5. Identical guns fire identical bullets horizontally at the same speed from the same height above level planes, one on the Earth and one on the Moon. Which of the following three statements is/are true? I. The horizontal distance traveled by the bullet is greater for the Moon. II. The flight time is less for the bullet on the Earth. III. The velocity of the bullets at impact are the same. A. III only C. I and III only E. I, II, III B. I and II only D. II and III only 6. A boat is able to move through still water at 20m/s. It makes a round trip to a town 3.0 km upstream. If the river flows at 5m/s, the time required for this round trip is: A. 120 s C. 200 s E. 320 s B. 150 s D. 300 s 7. A bomber flying in level flight with constant velocity releases a bomb before it is over the target. Neglecting air resistance, which one of the following is NOT true? A. The bomber is over the target when the bomb strikes B. The acceleration of the bomb is constant C. The horizontal velocity of the plane equals the vertical velocity of the bomb when it hits the target D. The bomb travels in a curved path E. The time of flight of the bomb is independent of the horizontal speed of the plane 8. A projectile is fired from ground level over level ground with an initial velocity that has a vertical component of 20 m/s and a horizontal component of 30 m/s. Using g= 10 m/s2, the distance from launching to landing points is: A. 40 m C. 80 m E. 180 m B. 60 m D. 120 m 9. An airplane is flying north at 500 km/h. It makes a gradual 1800 turn at constant speed, changing its direction of travel from north through east to south. The process takes 40 s. The average acceleration of the plane for this turn (in km/h·s) is: A. 12.5 km/h·s, north D. 25 km/h·s, north B. 12.5 km/h·s, east E. 25 km/h·s, south C. 12.5 km/h·s, south 10. A ferry boat is sailing at 12 km/h 300 W of N with respect to a river that is flowing at 6.0 km/h E. As observed from the shore, the ferry boat is sailing: A. 300 E of N C. 300 W of N E. none of these B. due N D. 450 E of N Rotation 1. A flywheel is initially rotating at 20 rad/s and has a constant angular acceleration. After 9.0 s it has rotated through 450 rad. Its angular acceleration is: A. 3.3 rad/s C. 5.6 rad/s E. 11 rad/s B. 4.4 rad/s D. 6.7 rad/s 2. A wheel rotates with a constant angular acceleration of π rad/s2. During a certain time interval its angular displacement is π rad. At the end of the interval its angular velocity is 2π rad/s. Its angular velocity at the beginning of the interval is: A. zero C. π rad/s E. 2π rad/s B. 1 rad/s D. π√2 rad/s 3. A wheel starts from rest and has an angular acceleration that is given by α(t) = (6 rad/s4)t2. The angle through which it turns in time t is given by: A. [(1/8)t4] rad C. [(1/2)t4] rad E. 12 rad B. [(1/4)t4] rad D. (t4) rad 4. A wheel starts from rest and has an angular acceleration that is given by α(t) = (6.0 rad/s4)t2. The time it takes to make 10 rev is: A. 2.8 s C. 4.0 s E. 5.3 s B. 3.3 s D. 4.7 s 5. A wheel starts from rest and has an angular acceleration that is given by α(t) = (6.0 rad/s4)t2. After it has turned through 10 rev its angular velocity is: A. 63 rad/s C. 89 rad/s E. 210 rad/s B. 75 rad/s D. 130 rad/s 6. A wheel of diameter 3.0 cm has a 4.0-m cord wrapped around its periphery. Starting from rest, the wheel is given a constant angular acceleration of 2.0 rad/s2. The cord will unwind in: A. 0.82 s C. 8.0 s E. 130 s B. 2.0 s D. 16 s 7. A particle moves in a circular path of radius 0.10 m with a constant angular speed of 5 rev/s. The acceleration of the particle is: A. 0.10π m/s2 C. 500π m/s2 E. 10π2 m/s2 B. 0.50 m/s2 D. 1000π2 m/s2 8. Two wheels are identical but wheel B is spinning with twice the angular speed of wheel A. The ratio of the magnitude of the radial acceleration of a point on the rim of B to the magnitude of the radial acceleration of a point on the rim of A is: A. 1 C. 1/2 E. 1/4 B. 2 D. 4 9. A phonograph turntable, initially rotating at 0.75 rev/s, slows down and stops in 30 s. The magnitude of its average angular acceleration in rad/s2 for this process is: A. 1.5 C. π/40 E. 0.75 B. 1.5π D. π/20 10. One revolution per minute is about: A. 0.0524 rad/s C. 0.95 rad/s E. 6.28 rad/s B. 0.105 rad/s D. 1.57 rad/s Tests by the theme Force 1. An example of an inertial reference frame is: A. any reference frame that is not accelerating B. a frame attached to a particle on which there are no forces C. any reference frame that is at rest D. a reference frame attached to the center of the universe E. a reference frame attached to Earth 2. When a certain force is applied to the standard kilogram its acceleration is 5.0 m/s2. When the same force is applied to another object its acceleration is one-fifth as much. The mass of the object is: A. 0.2 kg C. 1.0 kg E. 10 kg B. 0.5 kg D. 5.0 kg 3. An object placed on an equal-arm balance requires 12 kg to balance it. When placed on a spring scale, the scale reads 12 kg. Everything (balance, scale, set of weights and object) is now transported to the Moon where the free-fall acceleration is one-sixth that on Earth. The new readings of the balance and spring scale (respectively) are: A. 12 kg, 12 kg C. 12 kg, 2 kg E. 12 kg, 72 kg B. 2 kg, 2 kg D. 2 kg, 12 kg 4. Two objects, one having three times the mass of the other, are dropped from the same height in a vacuum. At the end of their fall, their velocities are equal because: A. anything falling in vacuum has constant velocity B. all objects reach the same terminal velocity C. the acceleration of the larger object is three times greater than that of the smaller object D. the force of gravity is the same for both objects E. none of the above 5. A feather and a lead ball are dropped from rest in vacuum on the Moon. The acceleration of the feather is: A. more than that of the lead ball D. 9.8 m/s2 B. the same as that of the lead ball E. zero since it floats in a vacuum C. less than that of the lead ball 6. An object rests on a horizontal frictionless surface. A horizontal force of magnitude F is applied. This force produces an acceleration: A. only if F is larger than the weight of the object B. only while the object suddenly changes from rest to motion C. always D. only if the inertia of the object decreases E. only if F is increasing 7. You stand on a spring scale on the floor of an elevator. Of the following, the scale shows the highest reading when the elevator: A. moves upward with increasing speed B. moves upward with decreasing speed C. remains stationary D. moves downward with increasing speed E. moves downward at constant speed 8. A man weighing 700 Nb is in an elevator that is accelerating upward at 4 m/s2. The force exerted on him by the elevator floor is: A. 71 N C. 410 N E. 990 N B. 290 N D. 700 N 9. A book rests on a table, exerting a downward force on the table. The reaction to this force is: A. the force of Earth on the book D. the force of the book on Earth B. the force of the table on the book E. the inertia of the book C. the force of Earth on the table 10. A lead block is suspended from your hand by a string. The reaction to the force of gravity on the block is the force exerted by: A. the string on the block D. the hand on the string B. the block on the string E. the block on Earth C. the string on the hand Kinetic energy and work 1. A 2-kg object is moving at 3 m/s. A 4-N force is applied in the direction of motion and then removed after the object has traveled an additional 5 m. The work done by this force is: A. 12 J C. 18 J E. 38 J B. 15 J D. 20 J 2. A sledge (including load) weighs 5000 N. It is pulled on level snow by a dog team exerting a horizontal force on it. The coefficient of kinetic friction between sledge and snow is 0.05. How much work is done by the dog team pulling the sledge 1000 m at constant speed? A. 2.5×104 J C. 5.0×105 J E. 5.0×106J B. 2.5×105J D. 2.5×106 J 3. Camping equipment weighing 6000 N is pulled across a frozen lake by means of a horizontal rope. The coefficient of kinetic friction is 0.05. How much work is done by the campers in pulling the equipment 1000 m if its speed is increasing at the constant rate of 0.20 m/2s ? A. −1.2×106 J C. 3.0×105 J E. 1.2×106 J B. 1.8×105 J D. 4.2×105 J 4. When a certain rubber band is stretched a distance x, it exerts a restoring force of magnitude F=Ax, where A is a constant. The work done by a person in stretching this rubber band from x= 0 to x=L, beginning and ending at rest, is: A. AL2 C. A+ 2L2 E. AL2/2 B. A+ 2L D. A/L 5. When a certain rubber band is stretched a distance x, it exerts a restoring force of magnitude F=ax+bx2, where a and b are constants. The work done in stretching this rubber band from x= 0 to x=L is: A. aL2+bLx3 C. a+ 2bL E. aL2/2 +bL3/3 B. aL+ 2bL2 D. bL 6. An ideal spring is hung vertically from the ceiling. When a 2.0-kg mass hangs at rest from it the spring is extended 6.0 cm from its relaxed length. A downward external force is now applied to the mass to extend the spring an additional 10 cm. While the spring is being extended by the force, the work done by the spring is: A. −3.6 J C. −3.4×10-5 J E. 3.6 J B. −3.3 J D. 3.3 J 7. An ideal spring is hung vertically from the ceiling. When a 2.0-kg block hangs at rest from it the spring is extended 6.0 cm from its relaxed length. A upward external force is then applied to the block to move it upward a distance of 16 cm. While the block is moving upward the work done by the spring is: A.−1.0 J C.−0.26 J E. 1.0 J B.−0.52 J D. 0.52 J 8. A 0.50-kg object moves on a horizontal frictionless circular track with a radius of 2.5 m. An external force of 3.0 N, always tangent to the track, causes the object to speed up as it goes around. If it starts from rest, then at the end of one revolution the radial component of the force of the track on it is: A. 19 N C. 47 N E. 96 N B. 38 N D. 75 N 9. A 2-kg block is attached to a horizontal ideal spring with a spring constant of 200 N/m. When the spring has its equilibrium length the block is given a speed of 5 m/s. What is the maximum elongation of the spring? A. 0 C. 5 m E. 100 m B. 0.05 m D. 10 m 10. A woman lifts a barbell 2.0 m in 5.0 s. If she lifts it the same distance in 10 s, the work done by her is: A. four times as great C. the same E. one-fourth as great B. two times as great D. half as great Potential energy and conservation of energy 1. Two particles interact by conservative forces. In addition, an external force acts on each particle. They complete round trips, ending at the points where they started. Which of the following must have the same values at the beginning and end of this trip? A. the total kinetic energy of the two-particle system B. the potential energy of the two-particle system C. the mechanical energy of the two-particle system D. the total linear momentum of the two-particle system E. none of the above 2. Two objects interact with each other and with no other objects. Initially object A has a speed of 5 m/s and object B has a speed of 10 m/s. In the course of their motion they return to their initial positions. Then A has a speed of 4 m/s and B has a speed of 7 m/s. We can conclude: A. the potential energy changed from the beginning to the end of the trip B. mechanical energy was increased by nonconservative forces C. mechanical energy was decreased by nonconservative forces D. mechanical energy was increased by conservative forces E. mechanical energy was decreased by conservative forces 3. Suppose that the fundamental dimensions are taken to be: force (F), velocity (V) and time (T). The dimensions of potential energy are then: A. F/T C. FV/T E. FV2/T2 B. FVT D. F/T2 4. An elevator is rising at constant speed. Consider the following statements: I. the upward cable force is constant II. the kinetic energy of the elevator is constant III. the gravitational potential energy of the Earth-elevator system is constant IV. the acceleration of the elevator is zero V. the mechanical energy of the Earth-elevator system is constant A. all five are true D. only I, II, and III are true B. only II and V are true E. only I, II, and IV are true C. only IV and V are true 5. A 700-N man jumps out of a window into afire net 10 m below. The net stretches 2 m before bringing the man to rest and tossing him back into the air. The maximum potential energy of the net, compared to its unstretched potential energy, is: A. 300 J C. 850 J E. 8400 J B. 710 J D. 7000 J 6. The thermal energy of a system consisting of a thrown ball, Earth, and the air is most closely associated with: A. the gravitational interaction of Earth and the ball B. the kinetic energy of the ball as a whole C. motions of the individual particles within the ball D. motions of individual particles within the ball and the air E. the kinetic energy of Earth as a whole 7. A block slides across a rough horizontal table top. The work done by friction changes: A. only the kinetic energy D. only the kinetic and potential energies B. only the potential energy E. only the kinetic and internal energies C. only the internal energy 8. A 25-g ball is released from rest 80 m above the surface of Earth. During the fall the total internal energy of the ball and air increases by 15 J. Just before it hits the surface its speed is A. 19 m/s C. 40 m/s E. 53 m/s B. 36 m/s D. 45 m/s 9. A 5-kg projectile is fired over level ground with a velocity of 200 m/s at an angle of 250 above the horizontal. Just before it hits the ground its speed is 150 m/s. Over the entire trip the change in the internal energy of the projectile and air is: A. +19,000 J C. +44,000 J E. 0 B. −19,000 J D. −44,000 J 10. A 0.75-kg block slides on a rough horizontal table top. Just before it hits a horizontal ideal spring its speed is 3.5 m/s. It compresses the spring 5.7 cm before coming to rest. If the spring constant is 1200 N/m, the internal energy of the block and the table top must have: A. not changed D. increased by 1.9 J B. decreased by 1.9 J E. increased by 2.6 J C. decreased by 2.6 J Center of mass and linear momentum 1. Which one of the following statements is true? A. the center of mass of an object must lie within the object B. all the mass of an object is actually concentrated at its center of mass C. the center of mass of an object cannot move if there is zero net force on the object D. the center of mass of a cylinder must lie on its axis E. none of the above 2. Block A, with a mass of 4 kg, is moving with a speed of 2.0 m/s while block B, with a mass of 8 kg, is moving in the opposite direction with a speed of 3 m/s. The center of mass of the two block-system is moving with a velocity of: A. 1.3 m/s in the same direction as A B. 1.3 m/s in the same direction as B C. 2.7 m/s in the same direction as A D. 1.0 m/s in the same direction as B E. 5.0 m/s in the same direction as A 3. A light rope passes over a light frictionless pulley attached to the ceiling. An object with a large mass is tied to one end and an object with a smaller mass is tied to the other end. Starting from rest the heavier object moves downward and the lighter object moves upward with the same magnitude acceleration. Which of the following statements is true for the system consisting of the two masses? A. The center of mass remains at rest. B. The net external force is zero. C. The velocity of the center of mass is a constant. D. The acceleration of the center of mass is g, downward. E. None of the above statements are true. 4. Two 4.0-kg blocks are tied together with a compressed spring between them. They are thrown from the ground with an initial velocity of 35 m/s, 450 above the horizontal. At the highest point of the trajectory they become untied and spring apart. About how far below the highest point is the center of mass of the two-block system 2.0 s later, before either fragment has hit the ground? A. 12 m B. 20 m C. 31 m D. Can’t tell because the velocities of the fragments are not given. E. Can’t tell because the coordinates of the highest point are not given. 5. A 2.0-kg block is attached to one end of a spring with a spring constant of 100 N/m and a 4.0-kg block is attached to the other end. The blocks are placed on a horizontal frictionless surface and set into motion. At one instant the 2.0-kg block is observed to be traveling to the right with a speed of 0.50 m/s and the 4.0-kg block is observed to be traveling to the left with a speed of 0.30 m/s. Since the only forces on the blocks are the force of gravity, the normal force of the surface, and the force of the spring, we conclude that: A. the spring is compressed at the time of the observation B. the spring is not compressed at the time of observation C. the motion was started with the masses at rest D. the motion was started with at least one of masses moving E. the motion was started by compressing the spring 6. A 2.0-kg mass is attached to one end of a spring with a spring constant of 100 N/m and a 4.0-kg mass is attached to the other end. The masses are placed on a horizontal frictionless surface and the spring is compressed 10 cm. The spring is then released with the masses at rest and the masses oscillate. When the spring has its equilibrium length for the first time the 2.0-kg mass has a speed of 0.36 m/s. The mechanical energy that has been lost to the instant is: A. zero C. 0.61 J E. 1.2 J B. 0.31 J D. 0.81 J 7. A 64-kg woman stands on frictionless level ice with a 0.10-kg stone at her feet. She kicks the stone with her foot so that she acquires a velocity of 0.0017 m/s in the forward direction. The velocity acquired by the stone is: A. 1.1 m/s forward D. 0.0017 m/s backward B. 1.1 m/s backward E. none of these C. 0.0017 m/s forward 8. A projectile inflight explodes into several fragments. The total momentum of the fragments immediately after this explosion: A. is the same as the momentum of the projectile immediately before the explosion B. has been changed into kinetic energy of the fragments C. is less than the momentum of the projectile immediately before the explosion D. is more than the momentum of the projectile immediately before the explosion E. has been changed into radiant energy 9. Sphere X, of mass 2 kg, is moving to the right at 10 m/s. Sphere Y, of mass 4 kg, is moving to the left at 10 m/s. The two spheres collide head-on. The magnitude of the impulse of X on Y is: A. twice the magnitude of the impulse of Y on X B. half the magnitude of the impulse of Y on X C. one-fourth the magnitude of the impulse of Y on X D. four times the magnitude of the impulse of Y on X E. the same as the magnitude of the impulse of Y on X 10. A student’s life was saved in an automobile accident because an airbag expanded in front of his head. If the car had not been equipped with an airbag, the windshield would have stopped the motion of his head in a much shorter time. Compared to the windshield, the airbag: A. causes a much smaller change in momentum B. exerts a much smaller impulse C. causes a much smaller change in kinetic energy D. exerts a much smaller force E. does much more work Rolling, torque, and angular momentum 1. A wheel of radius 0.5m rolls without sliding on a horizontal surface as shown. Starting from rest, the wheel moves with constant angular acceleration 6 rad/s2. The distance traveled by the center of the wheel from t = 0 to t = 3 s is: A. zero C. 13.5 m E. none of these B. 27 m D. 18 m 2. A thin-walled hollow tube rolls without sliding along the floor. The ratio of its translational kinetic energy to its rotational kinetic energy (about an axis through its center of mass) is: A. 1 C. 3 E. 1/3 B. 2 D. ½ 3. A 2.0-kg block travels around a 0.50-m radius circle with an angular velocity of 12 rad/s. The magnitude of its angular momentum about the center of the circle is: A. 6 kg · m2/s C. 48 kg/m2s E. 576 kg/m2 · s2 B. 12 kg · m2/s D. 72 kg · m2/s2 4. A 15-g paper clip is attached to the rim of a phonograph record with a radius of 30 cm, spinning at 3.5 rad/s. The magnitude of its angular momentum is: A. 1.4 × 10−3 kg · m2/s C. 1.6 × 10−2 kg · m2/s E. 1.1kg · m2/s B. 4.7 × 10−3 kg · m2/s D. 3.2 × 10−1 kg · m2/s
6. As a 2.0-kg block travels around a 0.50-m radius circle it has an angular speed of 12 rad/s. The circle is parallel to the xy plane and is centered on the z axis, a distance of 0.75m from the origin. The z component of the angular momentum around the origin is: A. 6 kg · m2/s C. 11 kg · m2/s E. 20 kg · m2/s B. 9 kg · m2/s D. 14 kg · m2/s 7. As a 2.0-kg block travels around a 0.50-m radius circle it has an angular speed of 12 rad/s. The circle is parallel to the xy plane and is centered on the z axis, 0.75m from the origin. The component in the xy plane of the angular momentum around the origin has a magnitude of: A. 0 C. 9 kg · m2/s E. 14 kg · m2/s B. 6 kg · m2/s D. 11 kg · m2/s
9. A 2.0-kg stone is tied to a 0.50-m long string and swung around a circle at a constant angular velocity of 12 rad/s. The circle is parallel to the xy plane and is centered on the z axis, 0.75m from the origin. The magnitude of the torque about the origin is: A. 0 C. 14 N · m E. 108 N · m B. 6 N · m D. 72 N · m 10. A cylinder of radius R = 6.0 cm is on a rough horizontal surface. The coefficient of kinetic friction between the cylinder and the surface is 0.30 and the rotational inertia for rotation about the axis is given by MR2/2, where M is its mass. Initially it is not rotating but its center of mass has a speed of 7.0m/s. After 2.0 s the speed of its center of mass and its angular velocity about its center of mass, respectively, are: A. 1.1 m/s, 0 C. 1.1 m/s, 98 rad/s E. 5.9 m/s, 98 rad/s B. 1.1 m/s, 19 rad/s D. 1.1 m/s, 200 rad/s Gravitation 1. In the formula F=Gm1m2/r2, the quantity G: A. depends on the local value of g B. is used only when Earth is one of the two masses C. is greatest at the surface of Earth D. is a universal constant of nature E. is related to the Sun in the same way that g is related to Earth 2. A particle might be placed 1. inside a uniform spherical shell of mass M, but not at the center 2. inside a uniform spherical shell of mass M, at the center 3. outside a uniform spherical shell of mass M, a distance from the center 4. outside a uniform solid sphere of mass M, a distance 2rfrom the center Rank these situations according to the magnitude of the gravitational force on the particle, least to greatest. A. All tie D. 1 and 2 tie, then 3, then 4 B. 1, 2, 3, 4 E. 1 and 2 tie, then 4, then 3 C. 1 and 2 tie, then 3 and 4 tie 3. To measure the mass of a planet with the same radius as Earth, an astronaut drops an object from rest (relative to the planet) from an altitude of one radius above the surface. When the object hits its speed is 4 times what it would be if the same experiment were carried out for Earth. In units of Earth masses, the mass of the planet is: A. 2 C. 8 E. 32 B. 4 D. 16 4. An astronaut on the Moon simultaneously drops a feather and a hammer. The fact that they land together shows that: A. no gravity forces act on a body in a vacuum B. the acceleration due to gravity on the Moon is less than on Earth C. in the absence of air resistance all bodies at a given location fall with the same acceleration D. the feather has a greater weight on the Moon than on Earth E. G= 0 on the Moon 5. An object is raised from the surface of Earth to a height of two Earth radii above Earth. Then: A. its mass increases and its weight remains constant B. both its mass and weight remain constant C. its mass remains constant and its weight decreases D. both its mass and its weight decrease E. its mass remains constant and its weight increases 6. A spherical shell has inner radius R1, outer radius R2, and mass M, distributed uniformly throughout the shell. The magnitude of the gravitational force exerted on the shell by a point mass particle of m, located a distance d from the center, inside the inner radius, is: A. 0 C. GMm/d2 E. GMm/(R1−d)2 B. GMm/R12 D. GMm/(R22−d2) 7. An astronaut finishes some work on the outside of his satellite, which is in circular orbit around Earth. He leaves his wrench outside the satellite. The wrench will: A. fall directly down to Earth B. continue in orbit at reduced speed C. continue in orbit with the satellite D. fly off tangentially into space E. spiral down to Earth 8. Consider the statement: “Earth moves in a stable orbit around the Sun and is therefore in equilibrium”. The statement is: A. false, because no moving body can be in equilibrium B. true, because Earth does not fall into or fly away from the Sun C. false, because Earth is rotating on its axis and no rotating body can be in equilibrium D. false, because Earth has a considerable acceleration E. true, because if it were not in equilibrium then buildings and structures would not be stable 9. Planet 1 and planet 2 are both in circular orbits around the same central star. The orbit of planet 2 has a radius that is much larger than the radius of the orbit of planet 1. This means that: A. the period of planet 1 is greater than the period of planet 2 and the speed of planet 1 is greater than the speed of planet 2 B. the period of planet 1 is greater than the period of planet 2 and the speed of planet 1 is less than the speed of planet 2 C. the period of planet 1 is less than the period of planet 2 and the speed of planet 1 is less than the speed of planet 2 D. the period of planet 1 is less than the period of planet 2 and the speed of planet 1 is greater than the speed of planet 2 E. the planets have the same speed and the same period 10. An artificial Earth satellite is moved from a circular orbit with radius R to a circular orbit with radius 2R. During this move: A. the gravitational force does positive work, the kinetic energy of the satellite increases, and the potential energy of the Earth-satellite system increases B. the gravitational force does positive work, the kinetic energy of the satellite increases, and the potential energy of the Earth-satellite system decreases C. the gravitational force does positive work, the kinetic energy of the satellite decreases, and the potential energy of the Earth-satellite system increases D. the gravitational force does negative work, the kinetic energy of the satellite increases, and the potential energy of the Earth-satellite system decreases E. the gravitational force does negative work, the kinetic energy of the satellite decreases, and the potential energy of the Earth-satellite system increases. Fluids 1. A long U-tube contains mercury (density = 14 × 103 kg/m3). When 10 cm of water (density = 1.0 × 103 kg/m3) is poured into the left arm, the mercury in the right arm rises above its original level by: A. 0.36 cm C. 14 cm E. 70 cm B. 0.72 cm D. 35 cm 2. An object hangs from a spring balance. The balance indicates 30 N in air and 20 N when the object is submerged in water. What does the balance indicate when the object is submersed in a liquid with a density that is half that of water? A. 20 N C. 30 N E. 40 N B. 25 N D. 35 N 3. A rock, which weighs 1400 N in air, has an apparent weight of 900 N when submerged in fresh water (998 kg/m3). The volume of the rock is: A. 0.14 m3 C. 0.90 m3 E. 9.2 × 10−2 m3 B. 0.60 m3 D. 5.1 × 10−2 m3 4. The dimensions of a wooden raft (density = 150 kg/m3) are 3.0m × 3.0m × 1.0m. What maximum load can it carry in seawater (density = 1020 kg/m3)? A. 1350 kg C. 9200 kg E. 24.300 kg B. 7800 kg D. 19.500 kg 5. A tin can has a volume of 1000 cm3 and a mass of 100 g. Approximately what mass of lead shot can it carry without sinking in water? A. 900 g C. 1000 g E. 980 g B. 100 g D. 1100 g 6. A block of wood weighs 160 N and has a specific gravity of 0.60. To sink it in fresh water requires an additional downward force of: A. 54 N C. 96 N E. 240 N B. 64 N D. 110 N 7. A solid has a volume of 8 cm3. When weighed on a spring scale calibrated in grams, the scale indicates 20 g. What does the scale indicate if the object is weighed while immersed in a liquid of density 2 g/cm3? A. 4 g C. 12 g E. Zero, since the object will float B. 10 g D. 16 g 8. A 210-g object apparently loses 30 g when suspended in a liquid of density 2.0g/cm3. The density of the object is: A. 7.0 g/cm3 C. 1.4 g/cm3 E. none of these B. 3.5g/cm3 D. 14 g/cm3 9. A 0.50-N metal sinker appears (as measured using a spring scale) to have a weight of 0.45 N when submerged in water. The specific gravity of the metal is: A. 6 C. 9 E. 12 B. 8 D. 10 10. One end of a cylindrical pipe has a radius of 1.5 cm. Water (density = 1.0×103 kg/m3) streams steadily out at 7.0m/s. The rate at which mass is leaving the pipe is: A. 2.5 kg/s C. 7.0 kg/s E. 7.0 × 103 kg/s B. 4.9 kg/s D. 48 kg/s Special theory of relativity 1. A millionairess was told in 1992 that she had exactly 15 years to live. However, if she travels away from the Earth at 0.8c and then returns at the same speed, the last New Year’s day the doctors expect her to celebrate is: A. 2001 C. 2007 E. 2017 B. 2003 D. 2010 2. Two events occur 100 m apart with an intervening time interval of 0.60 μs. The speed of a reference frame in which they occur at the same coordinate is: A. 0 C. 0.56c E. 1.8c B. 0.25c D. 1.1c 3. A rocket traveling with constant velocity makes a 8.4 × 1015 m trip in exactly one year. The proper time in years between events that mark the beginning and end of the trip is: A. 0.21 C. 1.0 E. 4.7 B. 0.46 D. 2.2 4. As a rocket ship moves by at 0.95c a mark is made on a stationary axis at the front end of the rocket and 9 × 10−8 s later a mark is made on the axis at the back end. The marks are found to be 100m apart. The rest length of the rocket is: A. 31m C. 100m E. 320m B. 78m D. 240m 5. A clock is moving along the x axis at 0.6c. It reads zero as it passes the origin (x = 0). When it passes the x = 180m mark on the x axis the clock reads: A. 0.60 μs C. 1.00 μs E. 1.67 μs B. 0.80 μs D. 1.25 μs 6. Relative to reference frame 1, reference frame 2 moves with speed v in the negative x direction. When the origins of the two frames coincide the clocks in both frames are set to zero. An event occurs at coordinate x1 and time t1 as measured in reference frame 1 and at coordinate x2 and time t2 as measured in frame 2. If 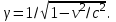 , then the coordinates and times of the event are related by: , then the coordinates and times of the event are related by:A. x2 = γ[x1 − vt1] and t2 = γ[t1 − vx1/c2] B. x2 = γ[x1 − vt1] and t2 = γ[t1 + vx1/c2] C. x2 = γ[x1 + vt1] and t2 = γ[t1 − vx1/c2] D. x2 = γ[x1 + vt1] and t2 = γ[t1 + vx1/c2] E. none of the above are correct 7. An event occurs at x = 500 m, t = 0.90 μs in one frame of reference. Another frame is moving at 0.90c in the negative x direction. The origins coincide at t = 0 and clocks in the second frame are zeroed when the origins coincide. The coordinate and time of the event in the second frame are: A. 500 m, 0.90 μs C. 740 m, 2.4 μs E. 590 m, −1.4 μs B. 1700 m, 5.5 μs D. 260 m, −0.60 μs 8. A certain particle has a kinetic energy of 3.2×10−10 J and a momentum of 1.7×10−18 kg ·m/s. Its mass is: A. 9.11 × 10−31 kg C. 4.5 × 10−27 kg E. 8.6 × 10−27 kg B. 2.7 × 10−27 kg D. 6.3 × 10−27 kg 9. An electron (m = 9.11 × 10−31 kg, q = 1.60 × 10−19 C) travels at 0.95c around a circular orbit perpendicular to a uniform 1.8-T magnetic field. The radius of its orbit is: A. 0.28 mm C. 1.1 mm E. 4.7 mm B. 0.90 mm D. 2.9 mm 10. An electron (m = 9.11 × 10−31 kg) has a speed of 0.95c. The magnitude of its momentum is: A. 2.6 × 10−22 kg · m/s C. 6.0 × 10−22 kg · m/s E. 8.8 × 10−22 kg · m/s B. 2.9 × 10−22 kg · m/s D. 8.3 × 10−22 kg · m/s Oscillations 1. A block attached to a spring oscillates in simple harmonic motion along the x axis. The limits of its motion are x = 10 cm and x = 50 cm and it goes from one of these extremes to the other in 0.25 s. Its amplitude and frequency are: A. 40 cm, 2 Hz C. 40 cm, 2 Hz E. 20 cm, 2 Hz B. 20 cm, 4 Hz D. 25 cm, 4 Hz 2. A certain spring elongates 9.0mm when it is suspended vertically and a block of mass M is hung on it. The natural angular frequency of this block-spring system: A. is 0.088 rad/s D. is 200 rad/s B. is 33 rad/s E. is 1140 rad/s C. cannot be computed unless the value of M is given 3. A 0.20-kg object attached to a spring whose spring constant is 500 N/m executes simple harmonic motion. If its maximum speed is 5.0 m/s, the amplitude of its oscillation is: A. 0.0020 m C. 0.20 m E. 250 m B. 0.10 m D. 25 m 4. A particle moves in simple harmonic motion according to x = 2 cos(50t), where x is in meters and t is in seconds. Its maximum velocity in m/s is: A. 100 sin(50t) C. 100 E. none of these B. 100 cos(50t) D. 200 5. A 3-kg block, attached to a spring, executes simple harmonic motion according to x = 2 cos(50t) where x is in meters and t is in seconds. The spring constant of the spring is: A. 1 N/m C. 150 N/m E. none of these B. 100 N/m D. 7500 N/m 6. A 0.25-kg block oscillates on the end of the spring with a spring constant of 200 N/m. If the system has an energy of 6.0 J, then the amplitude of the oscillation is: A. 0.06 m C. 0.24 m E. 6.9 m B. 0.17 m D. 4.9 m 7. A 0.25-kg block oscillates on the end of the spring with a spring constant of 200N/m. If the oscillation is started by elongating the spring 0.15m and giving the block a speed of 3.0m/s, then the maximum speed of the block is: A. 0.13 m/s C. 3.7 m/s E. 13 m/s B. 0.18 m/s D. 5.2 m/s 8. A mass-spring system is oscillating with amplitude A. The kinetic energy will equal the potential energy only when the displacement is: A. zero C. ±A/√2 E. anywhere between −A and +A B. ±A/4 D. ±A/2 9. The rotational inertia of a uniform thin rod about its end is ML2/3, where M is the mass and L is the length. Such a rod is hung vertically from one end and set into small amplitude oscillation. If L = 1.0m this rod will have the same period as a simple pendulum of length: A. 33 cm C. 67 cm E. 150 cm B. 50 cm D. 100 cm 10. Five hoops are each pivoted at a point on the rim and allowed to swing as physical pendulums. The masses and radii are hoop 1: M = 150 g and R = 50cm hoop 2: M = 200 g and R = 40cm hoop 3: M = 250 g and R = 30cm hoop 4: M = 300 g and R = 20cm hoop 5: M = 350 g and R = 10cm Order the hoops according to the periods of their motions, smallest to largest. A. 1, 2, 3, 4, 5 C. 1, 2, 3, 5, 4 E. 5, 4, 1, 2, 3 B. 5, 4, 3, 2, 1 D. 1, 2, 5, 4, 3 Waves 1. Water waves in the sea are observed to have a wavelength of 300m and a frequency of 0.07 Hz. The speed of these waves is: A. 0.00021 m/s C. 21 m/s E. none of these B. 2.1 m/s D. 210 m/s 2. Sinusoidal water waves are generated in a large ripple tank. The waves travel at 20 cm/s and their adjacent crests are 5.0 cm apart. The time required for each new whole cycle to be generated is: A. 100 s C. 2.0 s E. 0.25 s B. 4.0 s D. 0.5 s 3. A string carries a sinusoidal wave with an amplitude of 2.0 cm and a frequency of 100 Hz. The maximum speed of any point on the string is: A. 2.0 m/s B. 4.0 m/s C. 6.3 m/s D. 13 m/s E. unknown (not enough information is given) 4. A transverse traveling sinusoidal wave on a string has a frequency of 100 Hz, a wavelength of 0.040 m, and an amplitude of 2.0 mm. The maximum velocity in m/s of any point on the string is: A. 0.2 C. 4 E. 25 B. 1.3 D. 15 5. A transverse traveling sinusoidal wave on a string has a frequency of 100 Hz, a wavelength of 0.040 m, and an amplitude of 2.0 mm. The maximum acceleration in m/s2 of any point on the string is: A. 0 C. 395 E. 1600 B. 130 D. 790 6. Standing waves are produced by the interference of two traveling sinusoidal waves, each of frequency 100 Hz. The distance from the second node to the fifth node is 60 cm. The wavelength of each of the two original waves is: A. 50 cm C. 30 cm E. 15 cm B. 40 cm D. 20 cm 7. A string, clamped at its ends, vibrates in three segments. The string is 100 cm long. The wavelength is: A. 33.3 cm C. 150 cm E. need to know the frequency B. 66.7 cm D. 300 cm 8. The tension in a string with a linear mass density of 0.0010 kg/m is 0.40 N. A sinusoidal wave with a wavelength of 20 cm on this string has a frequency of: A. 0.0125 Hz C. 100 Hz E. 2000 Hz B. 0.25 Hz D. 630 Hz 9. When a 100-Hz oscillator is used to generate a sinusoidal wave on a certain string the wavelength is 10 cm. When the tension in the string is doubled the generator produces a wave with a frequency and wavelength of: A. 200 Hz and 20 cm C. 100 Hz and 20 cm E. 50 Hz and 14 cm B. 141 Hz and 10 cm D. 100 Hz and 14 cm 10. When a certain string is clamped at both ends, the lowest four resonant frequencies are 50, 100, 150, and 200 Hz. When the string is also clamped at its midpoint, the lowest four resonant frequencies are: A. 50, 100, 150, and 200 Hz D. 25, 50, 75, and 100 Hz B. 50, 150, 250, and 300 Hz E. 75, 150, 225, and 300 Hz C. 100, 200, 300, and 400 Hz |