Философиялык негздер. 1силлабус механика 2020-2021 СКАНЕР. Информация о дисциплине
 Скачать 1.43 Mb. Скачать 1.43 Mb.
|
|
7. ФОРМАТ ПРОВЕДЕНИЯ ДИСЦИПЛИНЫ И ТЕХНИЧЕСКИЕ ТРЕБОВАНИЯ: Методы, используемые на лекциях: презентация, интерактивные лекции, лекции с элементами обсуждения. Методы, используемые на практических занятиях: решение задач индивидуально и в группе, интерактивные дискуссии, работа в малых группах, коллективное обсуждение ситуаций. 8. ТАБЛИЦА СРСП, СРС:
ПРИМЕЧАНИЕ! СРСП проводится в соответствии с графикам, утвержденного вне расписания занятий а выполнение заданий СРС определяется в соответсвии с индивидуальным графиком преподавателя. 9. ТЕМАТИЧЕСКИЙ ПЛАН КУРСА 9.1 Лекции 9.1.1 Тема: Models in mechanics. Reference frames. Trajectory, the path length of the displacement vector Количество часов:1 Основные вопросы/план темы: 1. Models 2. Reference frames 3. Trajectory, path, displacement vector Тезисы лекции* Mechanics – the part of physics that studies the laws of mechanical motion and causes or alter the movement. Mechanical motion - a change of the position of a body with time in space. Mechanics is divided into three sections: 1) kinematics; 2) dynamics; 3) static. Kinematics studies the movement of bodies without considering the reasons that cause this movement. Dynamics studies the laws of motion of bodies and the reasons that cause a movement or its change. Static studies the laws of equilibrium of the system of bodies. Mechanics describes the motion of bodies, depending on the conditions of specific tasks using various physical models. The simplest model is a material point - a body having mass, the size of which can be neglected in comparison with the distance on which it is considered. Under the influence of bodies on each other's the body may be deformed, i.e. it can be changed its shape and size. Therefore, in the mechanics is introduced another model - absolutely solid body. Absolutely solid body is called the body, which under no circumstances can not be deformed and under all conditions, the distance between two points (or more precisely between two particles) of the body remains constant. Any movement of a rigid body can be represented as a combination of translational and rotational movements. Translational motion - a movement in which every line is rigidly associated with a moving body, it remains parallel to its original position. The rotational movement - a movement in which all points of the body are moving in circles, the centers of which lie on the same straight line, called the axis of rotation. The movement of bodies takes place in space and time. Therefore, it is necessary to know in order to describe the motion of a material point, the places where space, this point was, and at what times it was held a certain position. Mass point position is determined with respect to any other arbitrarily selected body, called the reference body. Since it is bound reference system - a set of coordinate system, clock and the reference body. In the general case the motion is determined by scalar equations 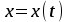 , , 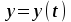 , , 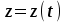 or or 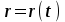 (1.1) (1.1)Equations (1.1) are called the kinematic equations of motion of a material point. The number of independent coordinates, completely defining the position of a point in space, are called the number of freedom degrees. If material point moves freely in space, then, as has been said, it has three freedom degrees, if it moves along a line, then it has one freedom degree (Fig. 1).  A 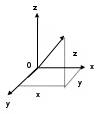 Figure 1. Freedom degrees of a material point Eliminating the equations (1.1), we obtain the equation of the trajectory of motion of a material point. The trajectory of a material point is the line described this point in space. Depending on the shape of the motion the path may be straight or curved. Let’s consider the motion of a point along an arbitrary trajectory (Fig. 2). The clock will start from the time when the point is in position A. The length of the portion of the trajectory AB is called the length of the path: s = s(t). Vector r = r – r0, drawn from the initial position of the moving point in its position at a given time (the increment of the radius vector of a point in the reporting period of time), is called the displacement. 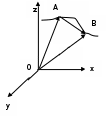 Figure 2. The motion of a point along an arbitrary trajectory In linear motion the displacement vector coincides with the corresponding portion of the path and the module |r| is equal to the traveled distance s. Вопросы для закрепления** - what is mechanics? - how many sections can the mechanics be divided into? - Describe each of the sections of mechanics Литература: Zhanturina N., Myasnikova. Fundamentals of Mechanics. – Aktobe, 2018. – 105 p. Yar-Mukhamedova G.Sh., Shunkeyev K.Sh., Zhanturina N.N. Mechanics. – Almaty: Kazakh University. -132 p. S. Thornton, A. Rex. Modern physics. –University of Virginia. 2013. – 613 p. I.E. Irodov. Problems in general physics. – Moscow, 1981. – 385 p. A. Beiser. Applied physics. – USA, 2003. – 138 p. DOI: 10.1036/0071425853 S. Holzner. Physics for dummies. – Hoboken, 2006. – 368 p. 9.1.2Тема: 2. Speed. Acceleration and its components Количество часов:1 Основные вопросы/план темы: 1. Velocity 2. Vector quantity 3. Acceleration Тезисы лекции* Velocity is a vector quantity that refers to "the rate at which an object changes its position." Velocity is a vector quantity. As such, velocity is direction aware. Speed is a scalar quantity and does not keep track of direction; velocity is a vector quantity and is direction aware. The vector average velocity 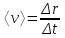 . (1.2) . (1.2)Average velocity vector coincides with the direction г. Average velocity decreases and indefinitely tends to a limiting value, which is called the instantaneous velocity v: 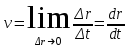 . (1.3) . (1.3)Instantaneous velocity v, therefore, is a vector quantity that is equal to the first derivative of the radius vector of a moving point in time. 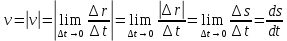 Thus, the instantaneous rate is the first derivative module paths over time: 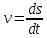 (1.4) (1.4)The length of the path traveled by a point in the time interval from t1 to t2, is given by the integral 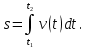 In the case of non-uniform motion is important to know how does the velocity change rapidly with time. Physical quantity that characterizes the rate of velocity change in magnitude and direction is called an acceleration. An average acceleration of the uniform motion in the interval from t to t+t is the vector quantity equal: 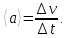 The instantaneous acceleration of the material point at time t is the limit of the average acceleration: 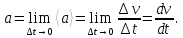 Thus, the acceleration is a vector equal to the first time derivative of velocity. Let’s expand the the vector Dv into two components. First component determines the rate of velocity change over time Dt by module and is called tangential: Dv = v1 - v. The second component Dvn of the vector Dv represents the change in velocity during Dt by direction and is called normal. The tangential component of the acceleration 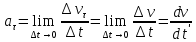 i.e. is the first time derivative of the velocity, thereby determining the speed of the rate of velocity change by module. The second component of the acceleration equal to 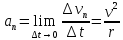 is called the normal component of acceleration and is perpendicular by the normal to trajectory to the center of curvature (it is also called the centripetal acceleration). The full acceleration of the body is the geometric sum of the tangential and normal components (Fig. 3): 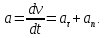  Figure 3. Components of acceleration Depending on the tangential and normal components of the acceleration the motion can be classified as follows: а = 0, an = 0 – uniform motion; a = a = const, an = 0 – nonuniform motion. At such motion 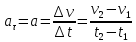 If at initial moment of the time t1 = 0 and initial velosity v1 = v0, then, take t2 = t and v2 = v, we obtasin a=(v—v0)/t, then 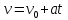 Integrating this equation in the range from zero to an arbitrary time t, we find that the length of the path traveled by a point, in the case of nonuniform motion 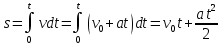 a = f(t), an = 0 – linear motion with variable acceleration; a = 0, an = const. At at = 0 the velocity by module does not change, but changes in direction. From formula an =v2/r It follows that the radius of curvature should be a constant. Consequently, the rotational motion is uniform; at = 0, an 0 – uniform curvilinear motion; at = const, an 0 – curved uniformly accelerated motion; a = f(t), an 0 – curvilinear motion with a variable acceleration. Вопросы для закрепления** - what is the formula for average speed? - how is velocity different from speed? - What is the formula of acceleration? Литература: 1. Zhanturina N., Myasnikova. Fundamentals of Mechanics. – Aktobe, 2018. – 105 p. 2. Yar-Mukhamedova G.Sh., Shunkeyev K.Sh., Zhanturina N.N. Mechanics. – Almaty: Ka-zakh University. -132 p. 3. S. Thornton, A. Rex. Modern physics. –University of Virginia. 2013. – 613 p. 4. I.E. Irodov. Problems in general physics. – Moscow, 1981. – 385 p. 5. A. Beiser. Applied physics. – USA, 2003. – 138 p. DOI: 10.1036/0071425853 6. S. Holzner. Physics for dummies. – Hoboken, 2006. – 368 p. 9.1.3 Тема: 3. Oscillations and waves Количество часов:1 Основные вопросы/план темы: 1. Harmonic oscillations 2. Differential equation 3. Pendulums Тезисы лекции* Oscillations are movements or processes that are characterized by a certain repeatability in time. Oscillations are called free (or intrinsic) if they are made at the expense of the initially reported energy with the subsequent absence of external influences on the oscillatory system (the system that makes the oscillations). The simplest type of oscillations are harmonic oscillations-oscillations, in which the oscillating quantity varies with time according to the law of the sine (cosine). The harmonic oscillations of quantity s are described by an equation of the type 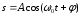 where А– the maximum of amplitude of the oscillation, 0 – circular (cyclic) frequency, – the initial phase of the oscillation at the time t = 0, (0t + ) is the oscillation phase at time t. The oscillation phase determines the value of the oscillating quantity at a given time. Since the cosine varies from +1 to -1, then s can take values from +A to -A. Certain states of the system performing harmonic oscillations are repeated after a time interval T, called the oscillation period, during which the oscillation phase receives an increment of 2, i.e. 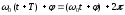 and 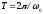 (8.2) (8.2)The inverse of the oscillation period, 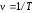 (8.3) (8.3)that is, the number of total oscillations per unit time called the frequency of oscillations. Comparing (8.2) and (8.3), we obtain 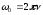 The unit of frequency is Hz (Hz): 1 Hz is the frequency of the periodic process, during which one cycle of the process takes place in 1 s. Вопросы для закрепления** - what is Oscillations? - Which equation describes harmonic oscillations? Литература: Zhanturina N., Myasnikova. Fundamentals of Mechanics. – Aktobe, 2018. – 105 p. Yar-Mukhamedova G.Sh., Shunkeyev K.Sh., Zhanturina N.N. Mechanics. – Almaty: Kazakh University. -132 p. S. Thornton, A. Rex. Modern physics. –University of Virginia. 2013. – 613 p. I.E. Irodov. Problems in general physics. – Moscow, 1981. – 385 p. A. Beiser. Applied physics. – USA, 2003. – 138 p. DOI: 10.1036/0071425853 S. Holzner. Physics for dummies. – Hoboken, 2006. – 368 p. 9.1.4 Тема: 4. First Newtons law. Mass. Forse Количество часов:1 Основные вопросы/план темы: 1. Inertia 2. Newtons first law 3. Newtons second law 4. Newtons third law Тезисы лекции* Newton's first law: An object in motion with a constant velocity will con-tinue in motion unless acted upon by some net external force. A body at rest is just a special case of Newton’s first law with zero velocity. Newton’s first law is often called the law of inertia and is also used to describe inertial reference frames. Newton's Second law: The net force applied to an object is directly proportional to its acceleration in an inertial reference frame. The constant of proportionality is called the mass of the object. In the system SI proportionality coefficient k = 1. Then 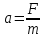 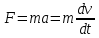 (2.1) (2.1)Newton's third law allows the transition from the dynamics of a separate material points to the dynamics of system of material points. This follows from the fact that the interaction of a system is lead to the pair of interaction forces between particles. Вопросы для закрепления** - How do you understand the concept of inertia? - Describe Newtons first law - Describe Newtons second law - Describe Newtons third law Литература: 1. 1. Zhanturina N., Myasnikova. Fundamentals of Mechanics. – Aktobe, 2018. – 105 p. 2. Yar-Mukhamedova G.Sh., Shunkeyev K.Sh., Zhanturina N.N. Mechanics. – Almaty: Ka-zakh University. -132 p. 3. S. Thornton, A. Rex. Modern physics. –University of Virginia. 2013. – 613 p. 4. I.E. Irodov. Problems in general physics. – Moscow, 1981. – 385 p. 5. A. Beiser. Applied physics. – USA, 2003. – 138 p. DOI: 10.1036/0071425853 6. S. Holzner. Physics for dummies. – Hoboken, 2006. – 368 p. 9.1.5 Тема: 5. Conservation of momentum. Center of mass Количество часов:1 Основные вопросы/план темы: 1. Conservation of momentum 2. Center of mass 3. The equation of variable mass body Тезисы лекции* The homogeneity of space is that the parallel displacement in the space of an isolated system of bodies as a whole, its physical properties and the laws of motion do not change, in other words, do not depend on the choice of the position of the origin of the inertial reference system. To derive the law of conservation of momentum, let’s consider some definitions. The collection of material points, considered as a single entity, is called the mechanical system. The forces of interaction between the material points of the mechanical system are called internal. The forces with which act on the material points of the system the external body are called external. The mechanical system of bodies on which no external force is called a closed (or isolated). If we have a mechanical system consisting of many bodies, according to Newton's third law, the forces acting between the two bodies are equal and are opposite directed, i.e. geometric sum of the internal forces is zero. Consider a mechanical system consisting of n bodies, mass and the velosity of which are m1, m2, ..., mn and v1, v2, ..., vn. Let F1, F2, ..., Fn - resultant of internal forces acting on each of the bodies, and F1, F2, ..., Fn - resultant of external forces. Let’s write Newton's second law for each of the N bodies (mechanical system):  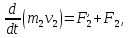 .. ..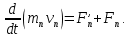 Adding these equations term by term, we obtain 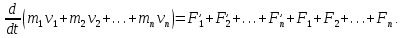 Вопросы для закрепления** - In which system is the conservation of momentum law satisfied? - Give the definition of the center of mass Литература: 1. Zhanturina N., Myasnikova. Fundamentals of Mechanics. – Aktobe, 2018. – 105 p. 2. Yar-Mukhamedova G.Sh., Shunkeyev K.Sh., Zhanturina N.N. Mechanics. – Almaty: Ka-zakh University. -132 p. 3. S. Thornton, A. Rex. Modern physics. –University of Virginia. 2013. – 613 p. 4. I.E. Irodov. Problems in general physics. – Moscow, 1981. – 385 p. 5. A. Beiser. Applied physics. – USA, 2003. – 138 p. DOI: 10.1036/0071425853 6. S. Holzner. Physics for dummies. – Hoboken, 2006. – 368 p. 9.1.6 Тема: 6. Kinetic and potential energies. Job. Power. Количество часов:1 Основные вопросы/план темы: 1. Kinetic energy 2. Potential energy 3. Work 4. Power Тезисы лекции* The kinetic energy of the mechanical system - the energy of the mechani-cal motion of the system. Energy – an universal measure of different forms of motion and interaction. With different forms of motion of matter is binded var-ious forms of energy: mechanical, thermal, electromagnetic, nuclear and so on. When the body moves rectilinearly and has a constant force F, which is at an angle а with a moving direction, then the work of this force is equal to the product of the projection of force F and the direction of movement, multiplied by the displacement of the point of force application  (3.1) (3.1) The kinetic energy of the mechanical system - the energy of the mechani-cal motion of the system. Вопросы для закрепления** - Give the definition of Kinetic and potential energies - Give the definition Job and Power. Литература: 1. Zhanturina N., Myasnikova. Fundamentals of Mechanics. – Aktobe, 2018. – 105 p. 2. Yar-Mukhamedova G.Sh., Shunkeyev K.Sh., Zhanturina N.N. Mechanics. – Almaty: Ka-zakh University. -132 p. 3. S. Thornton, A. Rex. Modern physics. –University of Virginia. 2013. – 613 p. 4. I.E. Irodov. Problems in general physics. – Moscow, 1981. – 385 p. 5. A. Beiser. Applied physics. – USA, 2003. – 138 p. DOI: 10.1036/0071425853 6. S. Holzner. Physics for dummies. – Hoboken, 2006. – 368 p. 9.1.7 Тема: 7. The energy conversation law Количество часов:1 Основные вопросы/план темы: 1. The derivation of energy conservation law 2. Conservative systems 3. The homogeneity of time Тезисы лекции* The total mechanical energy of the system remains constant. The law of conservation of mechanical energy: in a system of bodies, between which there are only conservative forces, the full mechanical energy is conserved, i.e., does not change with time... The mechanical systems, on bodies of which act only conservative forces (internal and external) are called conservative systems. The law of conserva-tion of mechanical energy can be formulated as follows: in conservative sys-tems, the total mechanical energy is conserved. The law of conservation of mechanical energy is linked to the homogene-ity of time. The homogeneity of the time is manifested in the fact that the laws of physics are invariant with respect to the choice of the time origin. For ex-ample, at body’s free fall in the gravitational field its speed and traveled dis-tance are depent only on the initial velocity and duration of free-fall of the body and does not depend on the time when body began to fall. There is an another kind of systems - dissipative systems, in which me-chanical energy is gradually reduced due to the transformation into another (non-mechanical) forms of energy. This process is called dissipation (or scat-tering) of the energy. Strictly speaking, all the systems in nature are dissipa-tive. Вопросы для закрепления** - what is the Conservative systems? - Give the definition of the energy conversation law Литература: 1. Zhanturina N., Myasnikova. Fundamentals of Mechanics. – Aktobe, 2018. – 105 p. 2. Yar-Mukhamedova G.Sh., Shunkeyev K.Sh., Zhanturina N.N. Mechanics. – Almaty: Ka-zakh University. -132 p. 3. S. Thornton, A. Rex. Modern physics. –University of Virginia. 2013. – 613 p. 4. I.E. Irodov. Problems in general physics. – Moscow, 1981. – 385 p. 5. A. Beiser. Applied physics. – USA, 2003. – 138 p. DOI: 10.1036/0071425853 6. S. Holzner. Physics for dummies. – Hoboken, 2006. – 368 p. 9.1.8 Тема: 8. Moment of inertia and the moment of force. The equation of the dynamics of the rotational motion of a rigid body Количество часов:1 Основные вопросы/план темы: 1. Moment of inertia 2. Moment of force 3. The equation of rotational motion Тезисы лекции* The moment J of inertia by an arbitrary axis is equal to the moment of inertia Jc with respect to the parallel axis through the center of mass of the body, added with the product of the mass m of the body and the square of the distance between the axes The moment of inertia of the system (the body) with respect to this axis is called a physical quantity, which is equal to the sum of products of mass n materials points of a system on the squares of their distances from the axis under consideration:  In the case of a continuous distribution of mass, this amount is reduced to the integral 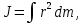 where the integration is over the volume of the body (Fig. 14). The value of r in this case is a function of position of the point with coordinates x, y, z. Вопросы для закрепления** - what is the moment of inertia and moment of force? - Give the definition of the equation of the dynamics of the rotational motion of a rigid body Литература: 1. Zhanturina N., Myasnikova. Fundamentals of Mechanics. – Aktobe, 2018. – 105 p. 2. Yar-Mukhamedova G.Sh., Shunkeyev K.Sh., Zhanturina N.N. Mechanics. – Almaty: Ka-zakh University. -132 p. 3. S. Thornton, A. Rex. Modern physics. –University of Virginia. 2013. – 613 p. 4. I.E. Irodov. Problems in general physics. – Moscow, 1981. – 385 p. 5. A. Beiser. Applied physics. – USA, 2003. – 138 p. DOI: 10.1036/0071425853 6. S. Holzner. Physics for dummies. – Hoboken, 2006. – 368 p. 9.1.9 Тема: 9. Moment of momentum and the law of its conservation. Deformation of a solid Количество часов:1 Основные вопросы/план темы: 1. Moment of momentum 2. Deformation of solid body Тезисы лекции* At rotation of a rigid body around a fixed axis z each individual point of the body moves by a circle of constant radius ri with some velocity vi. The ve-locity vi and impulse mvi are perpendicular to the radius r, i.e. the radius is a shoulder of a vector mivi. It can be shown that if the z-axis coincides with the principal axis of inertia, passing through the center of mass, then the vector equality 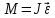 (4.5) (4.5)where J — principal moment of inertia (moment of inertia about the principal axis). The momentum of a material point A with respect to a fixed point O is called the physical quantity defined by the vector product: 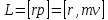 where r — the radius vector drawn from O to the point A; p = mv - the impulse of a material point (Fig. 18); L - pseudovector, its direction coincides with the direction of translational motion of the right screw as it rotates from r to p. The module of the momentum vector 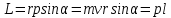 where — angle between vectors r and р, l — shoulder of the vector p with respect to the point O.  Angular momentum relative to the fixed z-axis is called a scalar quantity Lz, equal to the projection on the axis of the angular momentum, determined with respect to an arbitrary point O of the axis. The angular momentum L does not depend on the position of the point O on the axis z. Deformation is called elastic, if after the termination of the external force the body assumes its original size and shape. Deformations, which are stored in body after the termination of external forces, are called plastic. The force per unit cross-sectional area is called a strength:  (4.10) (4.10)If the force is perpendicular to the surface, the strength is called normal, if it is tangential to the surface - tangential. Вопросы для закрепления** - what is Moment of momentum? - What is the Deformation of solid body? Литература: 1. Zhanturina N., Myasnikova. Fundamentals of Mechanics. – Aktobe, 2018. – 105 p. 2. Yar-Mukhamedova G.Sh., Shunkeyev K.Sh., Zhanturina N.N. Mechanics. – Almaty: Ka-zakh University. -132 p. 3. S. Thornton, A. Rex. Modern physics. –University of Virginia. 2013. – 613 p. 4. I.E. Irodov. Problems in general physics. – Moscow, 1981. – 385 p. 5. A. Beiser. Applied physics. – USA, 2003. – 138 p. DOI: 10.1036/0071425853 6. S. Holzner. Physics for dummies. – Hoboken, 2006. – 368 p. 9.1.10 Тема: 10. Kepler's laws. Law of gravity Количество часов:1 Основные вопросы/план темы: 1. Kepler’s law 2. Law of gravity Тезисы лекции* Newton, studying the motion of celestial bodies, on the basis of Kepler's laws and the basic laws of dynamics discovered the universal law of gravitation: between any two material points is the force of mutual attraction,which is directly proportional to the product of the masses of these points (m1 and m2 and inversely proportional to the square of distances between them (r2) By the beginning of the XVII century, most of scientists were convinced in the validity of the heliocentric system of the world. Kepler (1571-1630), after processing and adding the results of numerous Danish astronomer T. Brahe (1546-1601) observations, stated laws of planetary motion: 1. Each planet moves by an ellipse, in one of focuses of which is the Sun. 2. The radius vector of the planet in equal intervals of time describes equal areas. 3. The ratio of squares of the periods of planets revolution around the sun are as the ratio of cubes of semi-major axes of their orbits. Later, Newton, studying the motion of celestial bodies, on the basis of Kepler's laws and the basic laws of dynamics discovered the universal law of gravitation: between any two material points is the force of mutual attraction,which is directly proportional to the product of the masses of these points (m1 and m2 and inversely proportional to the square of distances between them (r2):  (5.1) (5.1)This force is called gravitational (or universe attraction force). Gravitational forces are always attraction forces and are directed along a line passing through the interacting bodies. The proportionality coefficient G is the gravitational constant. Вопросы для закрепления** - Give definition of Kepler’s law - Give definition of Law of gravity Литература: 1. Zhanturina N., Myasnikova. Fundamentals of Mechanics. – Aktobe, 2018. – 105 p. 2. Yar-Mukhamedova G.Sh., Shunkeyev K.Sh., Zhanturina N.N. Mechanics. – Almaty: Ka-zakh University. -132 p. 3. S. Thornton, A. Rex. Modern physics. –University of Virginia. 2013. – 613 p. 4. I.E. Irodov. Problems in general physics. – Moscow, 1981. – 385 p. 5. A. Beiser. Applied physics. – USA, 2003. – 138 p. DOI: 10.1036/0071425853 6. S. Holzner. Physics for dummies. – Hoboken, 2006. – 368 p. 9.1.11 Тема: 11. Non-inertial frame of reference. Forces of inertia Количество часов:1 Основные вопросы/план темы: 1. The examples of noninertial reference frames 2. Inertia force 3. The general law of dynamics for noninertial reference systems Тезисы лекции* As already have been noted, Newton's laws are valid out only in inertial reference systems. Reference frames moving with respect to an inertial frame with acceleration, are called non-inertial. Considering the forces of inertia, the Newton's second law is valid for any frame of reference: the product of mass and acceleration of the body in the system is equal to the amount of all the forces acting on a given body (including inertial forces). Inertial forces at the same time should be such that, together with the forces F, caused by the influence of bodies on each other, they reported the body acceleration а' as it has in non-inertial reference frames, i. e.  Since F=ma (а — acceleration of the body in an inertial frame of reference), then 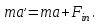 (5.7) (5.7)Let’s consider these cases. | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
