Курсовая работа по маркетингу. КУРСОВАЯ. Институт экономики и финансов
 Скачать 150.97 Kb. Скачать 150.97 Kb.
|
1 2 МИНИСТЕРСТВО ТРАНСПОРТА РОССИЙСКОЙ ФЕДЕРАЦИИ ФЕДЕРАЛЬНОЕ ГОСУДАРСТВЕННОЕ АВТОНОМНОЕ ОБРАЗОВАТЕЛЬНОЕ УЧРЕЖДЕНИЕ ВЫСШЕГО ОБРАЗОВАНИЯ «РОССИЙСКИЙ УНИВЕРСИТЕТ ТРАНСПОРТА (МИИТ)» (РУТ (МИИТ)) _____________________________________________________________________________ ИНСТИТУТ ЭКОНОМИКИ И ФИНАНСОВ Кафедра «Информационные системы цифровой экономики» Курсовая работа «КОМПЛЕКСНЫЙ АНАЛИЗ ВЗАИМОСВЯЗИ Финансово – экономических показателей деятельности организации» Дисциплина «Эконометрика» Вариант № 14
Москва – 2022 Введение Современные тенденции в развитии экономики влияют на формирование новой специфической среды, в которой осуществляется деятельность предприятия. В свою очередь, эти тенденции требуют комплексного анализа взаимосвязи финансово-экономических показателей. Знание методов и приемов экономического анализа позволяет разрабатывать эффективные стратегии и тактику функционирования предприятия. Актуальность данного исследования подтверждается необходимостью осуществления расчетов для последовательного и как можно более точного планирования деятельности компании, даже в условиях неопределенности. Цель курсовой работы состоит в анализе финансово-экономической деятельности организации. Задачи: Провести корреляционный анализ с помощью пакета «Анализ данных» в MS «Excel». Провести регрессионный анализ с помощью пакета «Анализ данных» в MS «Excel». Сочетание теоретической и практической частей в данном исследовании можно считать лучшим вариантом для формирования объективного представления о взаимосвязях финансово-экономических показателей и стратегического развития предприятия. В первой главе данной курсовой работы будут рассмотрены теоретические основы и методы эконометрики, позволяющие выявить существующие связи между параметрами модели и внешними факторами. Во второй главе представлена расчетная часть, исходя из которой мы сможем сделать вывод о качестве финансово-экономических показателей организации. Результаты работы можно использовать для формирования рекомендаций фирмам по конкретному профилю. Глава 1. Теоретическая часть В ходе выполнения анализа взаимосвязи финансово-экономических показателей деятельности организации для достижения цели данной работы – будут использованы приведенные ниже методы исследования, анализа и прогнозирования. Ставя цель – выбор наилучшего уравнения множественной линейной регрессии, эконометрика прежде всего связана с методами регрессии и корреляции. Регрессионный анализ – это основной математико-статистический инструмент в эконометрике. Регрессия представляет собой зависимость среднего значения величины y от другой величины x или нескольких величин xi. Количество факторов, которые включены в уравнение регрессии определяет вид регрессии, которая может быть простой (парной) или множественной. Простая регрессия представляет собой регрессию между двумя переменными y и x, т. е. модель вида: y = f(x), где y – зависимая переменная (результативный признак), x – независимая или объясняющая переменная. Множественная регрессия соответственно представляет собой регрессию результативного признака с двумя или большим числом факторов, т. е. модель вида: y = f (x1, x2, … , xk). Корреляционный анализ – это раздел математической статистики, посвященной изучению взаимосвязи между зависимыми переменными. Корреляционная зависимость или корреляция – это связь, при которой каждому значению независимой переменной x соответствует определенное математическое ожидание (среднее значение) зависимой переменной y. Корреляционная связь бывает прямая (с увеличением (уменьшением) значений факторного признака x происходит увеличение (уменьшение) значений результативного признака y) и обратная (с увеличением (уменьшением) значений факторного признака x происходит уменьшение (увеличение) значений результативного признака y). Корреляционная матрица. Мультиколлинеарность независимых переменных. Корреляционную матрицу строим с помощью пакета «Анализ данных» инструмент «Корреляция». Элементы корреляционной матрицы являются коэффициентами парной корреляции между соответствующими переменными, которые находятся по формуле: 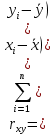 (1.1) (1.1)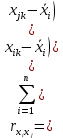 (1.2) (1.2)Для определения силы (тесноты) корреляционной связи между объясняющими переменными пользуются шкалой Чеддока (табл.1). Таблица 1. Шкала Чеддока.
Матрица межфакторных корреляций — это часть корреляционной матрицы, содержащей коэффициенты парной корреляции между объясняющими переменными. Мультиколлинеарность – это нарушение требования теоремы Гаусса – Маркова о линейной независимости факторных переменных x1, x2, xm. На практике говорят о мультиколлинераности, когда три и более независимые переменные сильно коллиниарны друг с другом. Тестируется по формуле: 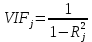 (1.3) (1.3)Если коэффициент VIF > 10, то независимая переменная xj отвечает за мультиколлинеарность и её нужно исключить. Уравнение множественной линейной регрессии с двумя независимыми переменными в натуральном масштабе. Уравнение множественной линейной регрессии с двумя независимыми переменными имеет вид: 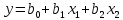 Параметры b найдем с помощью пакета «Анализ данных» инструмент «Регрессия». Проверка качества уравнения множественной линейной регрессии (средняя относительная ошибка аппроксимации, F – критерий, t – критерий, интервальные оценки коэффициентов регрессии) Для оценки математической точности уравнения пользуются средней относительной ошибкой аппроксимации: 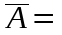 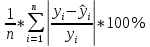 (1.4) (1.4)Для принятия решения о точности уравнения пользуются таб.2. Таблица 2. Характеристика точности уравнения.
Проверка статистической значимости уравнения регрессии в целом осуществуляются с помощью F – критерия Фишера. Расчетное значение критерия находится по формуле: 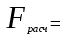 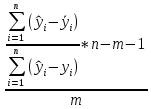 (1.5) (1.5)Табличное (критическое) значение Fтабл , находится по таблице критических значений распределения Фишера – Снедекора (F – распределения) по уровню значимости a и двум числам степеней свободы df1 = m и df2 = n – m – 1 или с помощью встроенной функции Excel «FРАСПОБР». Если Fрасч > Fтабл, то с вероятностью ошибки a уравнение регрессии признается в целом статистически значимым (адекватно описывающем исходные данные). В противном случае (Fрасч < Fтабл) уравнение считается незначимым в целом. Проверка статистической значимости оценок параметров b0, b1 проивзодится с помощью t – критерия Стьюдента. Находятся расчетные значения критериев: 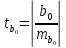 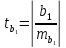 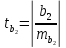 Теоретическое значение критерия tтабл находится по таблице критических значений распределения Стьюдента по уровню значимости по уровню значимости a и числу степеней свободы df = n – m – 1 или с помощью встроенной функции Excel «СТЬЮДРАСПОБР». Если | tbj | > tтабл, то с вероятностью ошибки a оценка параметра уравнения регрессии bj(j = 0,1) признается статистически значимой. В противной случае | tbj | < tтабл – bj статистически незначим. Интервальные оценки (доверительные интервалы) параметров уравнения регрессии имеют вид: 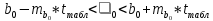 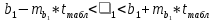 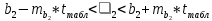 C надежностью (вероятностью) y = 1 – a они покрывают истинные параметры 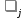 . . Если границы некоторых доверительных интервалов имеют разные знаки, соответствующий параметр уравнения статистически незначим. Анализ остатков (проверка предпосылок теоремы Гаусса – Маркова) Согласно экономической модели: 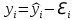 остатки 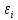 находятся как разность между фактическими (наблюдаемыми) и теоретическими значениями зависимой переменной: находятся как разность между фактическими (наблюдаемыми) и теоретическими значениями зависимой переменной: 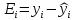 Остатки должны удовлетворять требованиям D, E теоремы Гаусса – Маркова. Проверка требования D. Числовой оценкой математического ожидания M( 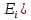 является среднее значение является среднее значение 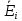 . Для выполнения требования M( . Для выполнения требования M(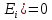 необходимо, чтобы необходимо, чтобы 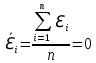 Дисперсия остатков 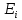 должна быть одинаковой для всех значений должна быть одинаковой для всех значений 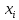 (свойство гомоскедастичности). Если условие не соблюдается, то имеет место гетероскедастичность остатков. (свойство гомоскедастичности). Если условие не соблюдается, то имеет место гетероскедастичность остатков. Точечная (числовая) оценка дисперсии остатков 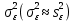 находится по формуле: находится по формуле: 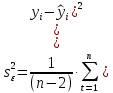 Проверка требования E – для разных наблюдений остатки 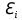 некоррелированы (независимы). некоррелированы (независимы). Метод проверки требования – критерий Дарбина – Уотсона: 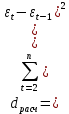 Где 0 ≤ 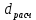 ≤ 4 ≤ 4Теоретические значения Дарбина – Уотсона находятся по таблице критических значений по объему выборки n, числу степеней свободы df = 1 и уровню значимости a. С помощью критических значений числовой промежуток (0;4) разбивается на пять отрезков и принимается решение о независимости остатков. Принятие решения о зависимости остатков
На практике в случае, когда статистика критерия 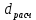 попадает в зону неопределённости, обычно признается наличии автокорреляции в остатках. попадает в зону неопределённости, обычно признается наличии автокорреляции в остатках. Тест Харке – Бера Тест Харке – Бера – это статистический тест, проверяющий ошибки наблюдений на нормальность посредством сверки их третьего момента (асимметрия) и четвертого момента (эксцесс) с моментами нормального распределения. Тест выглядит следующим образом: 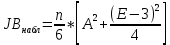 Где K = 2; a = 0,05; 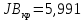 Если 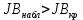 , то остатки не подчиняются нормальному закону распределения. , то остатки не подчиняются нормальному закону распределения. В противном случае,когда 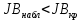 – остатки подчиняются нормальному закону распределения. – остатки подчиняются нормальному закону распределения. Коэффициент детерминации, коэффициент множественной корреляции. Интервальная оценка коэффициента множественной корреляции. Для оценки качества полученного уравнения регрессии будем использовать коэффициент детерминации R2. Он оценивает долю влияния вариации признака y, обусловленную изменением значений признака x. Чем ближе значение R2 к единице, тем больше признак x участвует в формирование значений y. 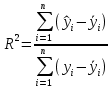 Проверка статистической значимости коэффициента детерминации производится с помощью F – критерия Фишера. Если Fрасч > Fтабл, то коэффициент детерминации признается статистически значимым. Коэффициент множественной корреляции характеризует тесноту множественной линейной связи и находится по формуле: 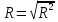 Чтобы сделать вывод по коэффициенту множественной корреляции воспользуемся таблицей 3. Таблица 3.
Интервальная оценка коэффицента множественной корреляции R находится с помощью z – пребразования Фишера. 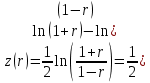 Предварительно устаналивается интервальная оценка для z в виде: 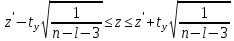 Где l - порядок коэффициента корреляции (для коэффициента парной корреляции l = 2); n – объем выборки; y -вероятность выполнения неравенства; ty вычисляется по таблице значений интегральной функции Лапласа из условия Ф(ty) = y. Значение z’ определяется по таблице z – преобразования с помощью встроенной функции Excel «ФИШЕР». Оценка силы влияния независимых переменных на результат с помощью бета- и дельта коэффициентов. Частные коэффициенты детерминации, средние и частные коэффициенты эластичности. Бета-коэффициент показывает, на какую часть величины среднеквадратического отклонения изменится переменнаяyс изменением соответствующей независимой переменной xj на величину своего среднеквадратического отклонения при фиксированном уровне значений остальных факторных переменных. Находятся по формуле: 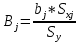 Среднеквадратические отклонения найдены по формулам: 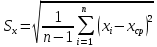 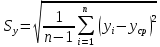 Или с помощью встроенной функции Excel «СТАНДОТКЛОН». Дэльта-коэффициенты показывают долю влияния фактора в суммарном влиянии всех факторов можно оценить по величине дельта-коэффициентов: Найдены по формулам: 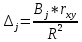 Где 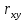 – коэффициент парной корреляции между фактором xj и исследуемой переменной y. – коэффициент парной корреляции между фактором xj и исследуемой переменной y.Для оценки влияния факторного признака х на результативный признак y вычисляют средние и частные коэффициенты эластичности. Средние коэффициенты эластичности показывают, на сколько процентов изменяется y при увеличении xна один процент и позволяет выявить общегрупповые закономерности. Находятся по формуле: 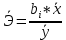 Частные коэффициенты эластичности показывают, на сколько процентов изменится yi, если xi увеличится на 1%. Находятся по формуле: 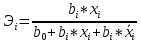 Здесь b0, b1– параметры уравнения регрессии, xi - i-е наблюдение независимой переменной (i = 1, 2, ..., n). Прогнозное значение зависимой переменной. Интервальная оценка. Найдем прогнозное значение признака Y при прогнозном значении X, составляющем 110 % от его среднего уровня, оценим точность прогноза по стандартной ошибке и доверительному интервалу. В прогнозных расчетах предсказываемое значение yпр. определяется как точечный прогноз 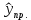 путем подстановки в уравнение регрессии соответствующего прогнозного значения xпр.. Точечный прогноз дополняется построением интервальной оценки (доверительного интервала). путем подстановки в уравнение регрессии соответствующего прогнозного значения xпр.. Точечный прогноз дополняется построением интервальной оценки (доверительного интервала). Найдем xпр. по формуле: 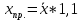 Найдем yпр.: 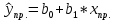 Интервальная оценка прогноза имеет вид: 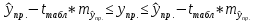 Здесь tтабл – критическое значение распределения Стьюдента, найденное по уровню значимости a и числу степеней свободы df = n – 2. Cредняя стандартная ошибка прогноза равна: 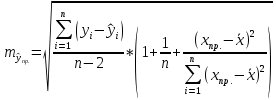 Парное линейное уравнение регрессии. Уравнение парной линейной регрессии имеет вид: 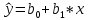 Где b0, b1 – параметры уравнения, найденные с помощью пакета «Анализ данных» инструмента «Регрессия» Оценка качества уравнения парной линейной регрессии. Скорректированный коэффициент детерминации: 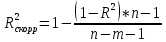 Скорректированный коэффициент детерминации обладает свойством 0 < 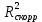 < 1. < 1. Коэффициент парной корреляции находится по формуле: 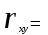 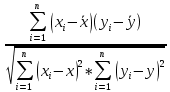 Коэффициент парной корреляции 𝒓𝒚𝒙 служит мерой линейной корреляционной зависимости между величинами y и x , при условии, что на формирование их значений оказывают влияние некоторые другие, неучтенные факторы. Для определения тесноты (силы) линейной корреляционной зависимости воспользуемся шкалой Чеддока (таб.1) Фиктивные переменные. Уравнение сдвига, наклона, сдвига – наклона. Для количественного описания качественных или категориальных переменных вводят фиктивные переменные: dummy переменные (d или z). Существует 2 подхода: Матрица статистических наблюдений по заданному признаку делится на части и для каждой части строится свое уравнение регрессии. Недостатком является требование большего количества объектов наблюдений. Построение уравнений с переменной структурой для всей статистической совокупности. В нашем случае: 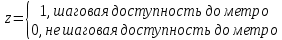 Уравнение сдвига имеет вид: 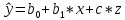 Уравнение наклона имеет вид: 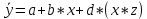 Уравнение сдвига – наклона имеет вид: 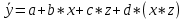 Выбор наилучшего уравнения производится по наибольшему скорректированному коэффициенту детерминации. 1 2 | ||||||||||||||||||||||||||||||||||||||||||||||||||

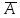 , %
, %