Курсовая работа по маркетингу. КУРСОВАЯ. Институт экономики и финансов
 Скачать 150.97 Kb. Скачать 150.97 Kb.
|
1 2 Расчетная часть. Исходные данные:
Корреляционная матрица. Мультиколлинеарность независимых переменных. Корреляционную матрицу строим с помощью пакета «Анализ данных» инструмент «Корреляция».
Проверим мультиколлинеарность:
Вывод: коэффициент VIF > 10, следовательно, переменные X5, X9, X11 отвечают за мультиколлинеарность и их нужно исключить. Корреляционная матрица имеет вид:
Взаимосвязь зависимой и объясняющей переменной Вывод: между объясняющей переменной X16 и зависимой переменной Y связь практически отсутствует, т. к. для него абсолютные значения коэффициентов корреляции меньше 0,2. Между объясняющей переменной X39 и зависимой переменной Y связь сильная (тесная), т. к. для него абсолютные значения коэффициентов корреляции попадают в интервал от 0,7 lj 0,95. Уравнение множественной линейной регрессии c двумя независимыми переменными. 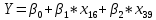 Y = 161,90 – 1,29 * 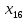 + 1,84 * + 1,84 * 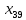 Проверка качества уравнения множественной линейной регрессии (средняя относительная ошибка аппроксимации, F – критерий, t – критерий, интервальные оценки коэффициентов регрессии) Средняя ошибка аппроксимации: 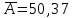 Вывод: средняя ошибка аппроксимации равна 50,37%, что свидетельствует о неудовлетворительной точности уравнения (табл.2. интервал более 50 %). F – критерий Фишера: Fрасч = 6,47 Fтабл = (a; df1; df2) = (0,05; 2; 24) = 3,40 Вывод: так как Fрасч > Fтабл (6,47 > 3,40), то уравнение регрессии в целом статистически значимо (адекватно описывает исходные данные) Проверим статистическую значимость отдельных параметров уравнения регрессии с помощью критерия Стьюдента.
Найдем t – табличное: tтабл = (a; df2) = (0,05; 24) = 2,06 Вывод: 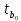 < tтабл (1,74 <2,06) и с вероятностью 0,05 оценка параметра уравнения b0 статистически незначима; < tтабл (1,74 <2,06) и с вероятностью 0,05 оценка параметра уравнения b0 статистически незначима; 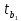 < tтабл (-1,27 < 2,06) и с вероятностью 0,05 оценка параметра уравнения b1 статистически незначима; < tтабл (-1,27 < 2,06) и с вероятностью 0,05 оценка параметра уравнения b1 статистически незначима; 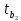 < tтабл (3,60 < 2,06) и с вероятностью 0,05 оценка параметра уравнения b2 статистически значима. < tтабл (3,60 < 2,06) и с вероятностью 0,05 оценка параметра уравнения b2 статистически значима.Найдем интервальные оценки параметров уравнения: 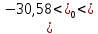 354,37 354,37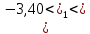 0,81 0,81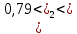 2,90 2,90Вывод: b0 = 161,90 и с вероятностью 0,95 находится в пределах от -30,58 до 354,37; b1 = -1,29 и с вероятностью 0,95 находится в пределах от -3,40 до 0,81; b2 = 1,84 и с вероятностью 0,95 находится в пределах от 0,79 до 2,90. Анализ остатков регрессионной модели (равенство нулю математического ожидания, постоянство дисперсии остатков, независимость остатков, подчинение остатков нормальному закону распределения). Проверим требование D теоремы Гаусса – Маркова: Среднее значение остатков: 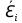 = 0,00 = 0,00Вывод: среднее значение остатков равно нулю, что свидетельствует об отсутствии систематической ошибки. На графике (рис.) точки внутри горизонтальной полосы, симметричной оси абсцисс. 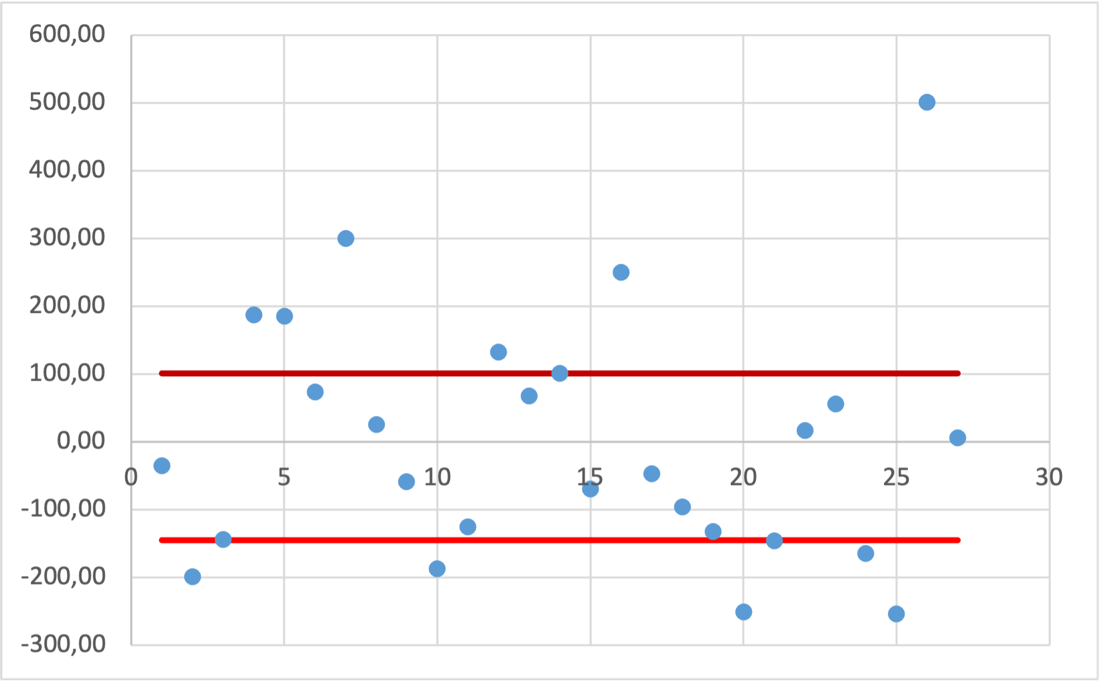 Рисунок 1. График остатков. Вывод: так как горизонтальная полоса несимметрична оси абсцисс и остатки внутри этой полосы распределены неравномерно, дисперсия остатков непостоянна. Точечная оценка дисперсии равна: 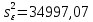 Критические значения распределения X2 Пирсона найдем по числу степеней свободы: Df = n – m – 1 = 24 И уровням значимости: a1 = 1 – a/2 = 0,98; a2 = a/2= 0,025 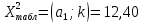 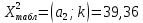 Тогда доверительный интервал остатков имеет вид: (21337,47;67729,99) Проверим требование E теоремы Гаусса – Маркова – для разных наблюдений остатки независимы. Воспользуемся критерием Дарбина – Уотсона: Dрасч = 1,82 Для уравнения множественной линейной регрессии теоретические значения критерия Дарбина – Уотсона найдены по таблице критических значений (приложение 5) по объему выборки n = 27, числу степеней свободы df = 2 и уровню значимости a = 0,05. dL = 1,24 dU = 1,56
Вывод: так как dрасч попадает в интервал от 1,56 до 2,44, то автокорреляция остатков отсутствует A = 0,88 Э = 0,87 JBрасч = 8,63 JBнабл = 5,99 Вывод: так как JBрасч > JBнабл (8,63 > 5,99), то остатки не подчиняются нормальному закону распределения. Коэффициент детерминации, коэффициент множественной корреляции. Их статистическая значимость. Интервальная оценка коэффициента множественной корреляции. R2 = 0,3502 Вывод: коэффициент детерминации показывает, что факторы «индекс потребительских расходов» (x16) и «расходы на рекламу (x39) на 35,02% объясняют формирование значений показателя «среднее количество клиентов в месяц» (Y). Оценим статистическую значимость коэффициента детерминации с помощью критерия Фишера: Fрасч = 6,47 Найдем F – табличное: Fтабл = (a; df1; df2) = (0,05; 2; 24) = 3,40 Вывод: поскольку Fрасч > Fтабл, уравнение статистически значимо. Коэффициент множественной корреляции: R = 0,5918 Вывод: между факторами «индекс потребительских расходов» (X16) и «среднее количество клиентов в месяц» (Y) существует сильная (тесная) множественная корреляционная зависимость. Интервальная оценка (доверительный интервал) коэффициента множественной корреляции находится с помощью z – преобразования Фишера. 0,25 ≤ z ≤ 1,11 0,25 ≤ R ≤ 0,80 Вывод: коэффициент множественной корреляции примерно равен 0,5918 и с вероятностью 0,95 находится в пределах от 0,25 до 0,80. Сила влияния независимых переменных на результат с помощью бэта и дельта коэффициентов, частных коэффициентов детерминации и частных коэффициентов эластичности.
Вывод: дельта – коэффициент показывает, что фактор «индекс потребительских расходов» (X16) на -0,01 влияет на среднее количество клиентов в месяц (Y) в суммарном влияние всех факторов, включенных в модель. Дельта- коэффициент показывает, что фактор «расходы на рекламу» (X39) на 1,01 влияет на среднее количество клиентов в месяц (Y) в суммарном влияние всех факторов, включенных в модель. Вывод: средний коэффициент эластичности (Э16) показывает, что при увеличении индекса потребительских расходов (X16) на 1% среднее количество клиентов в месяц уменьшится на 22%. Cредний коэффициент эластичности (Э39) показывает, что при увеличении расходов на рекламу (X39) на 1% среднее количество клиентов в месяц увеличится на 79%.
Вывод: частный коэффициент эластичности Э16 показывает, что при увеличении индекса потребительских расходов (X16) на 1% наибольший рост среднего количества клиентов в месяц отмечается на предприятие 8 (Э8 = 7,27), наименьший на предприятие 26 (Э26 = -17,18). На предприятие 4 и 10 индекс потребительских расходов такой же, как в среднем по группе предприятий (Э4 = -0,22; Э10 = -0,22). При неизменности расходов на рекламу (X39). Частный коэффициент эластичности Э39 показывает, что при увеличении расходов на рекламу (X39) на 1% наибольший рост среднего количества клиентов в месяц отмечается на предприятие 5,8,24,25 (Э5 = 0,89; Э8 = 0,86; Э24 = 0,88; Э25 = 0,86), наименьший на предприятие 14 (Э14 = 0,46). На предприятие 1 расходы на рекламу такие же, как в среднем по группе предприятий (Э1 = 0,79). При неизменности индекса потребительских расходов (X16). Прогнозные значения зависимой переменной Значения независимых переменных составляют 110% от среднего уровня. Прогнозное значение x: 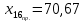 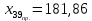 Прогнозное значение y: 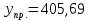 2.10. Построение уравнения парной линейной регрессии для независимой переменной, наиболее тесно связанной с зависимой Наиболее тесно связана c Y независимая переменная X39. Параметры уравнения равны: b0 = 118,23 b1 = 1,60 Уравнение парной линейной регрессии имеет вид: 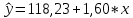 2.11. Оценка качества уравнения парной линейной регрессии: коэффициент детерминации, скорректированный коэффициент детерминации, коэффициент парной корреляции. R2 = 0,3067 Вывод: коэффициент детерминации показывает, что фактор «расходы на рекламу» (x39) на 30,67 % объясняют формирование значений показателя «среднее количество клиентов в месяц» (Y), а остальные 69,33 % оказывает влияние на другие факторы. Rскор. = 0,2790 Найдем F – критерий Фишера: Fрасч = 11,06 Fтабл = 4,24 Вывод: поскольку Fрасч > Fтабл (11,06 > 4,24) – уравнение статистически значимо (адекватно описывает исходные данные). Коэффициент парной корреляции: rxy = 0,55 Вывод: величина коэффициента корреляции, находящиеся в пределах от 0,7 до 0,95 согласно шкале Чеддока свидетельствует о тесной линейной корреляционной связи между расходами на рекламу и средним количеством клиентов в месяц. 2.12. Фиктивные переменные. Для независимой переменной и фиктивной переменной построить структурные уравнения сдвига, наклона и сдвига- наклона.
Наилучшее уравнение выбирается по наибольшему значению скорректированного коэффициента детерминации. Вывод: уравнение с фиктивной переменной сдвига является наилучшим, т. к. ему соответствует скорректированный коэффициент детерминации с наибольшим значением (0,4891) Сюда рисунок 2. Заключение Целью данной курсовой работы был анализ финансово-экономической деятельности организации. Проведение корреляционного анализа с помощью пакета «Анализ данных» в MS «Excel» позволило рассмотреть подробно теоретические основы и методы эконометрики, позволяющие выявить существующие связи между параметрами модели и внешними факторами. Проведение регрессионного анализа с помощью пакета «Анализ данных» в MS «Excel» позволило сделать выводы о качестве финансово-экономических показателей предприятия. Сочетание теоретической и практической частей в данном исследовании действительно можно считать лучшим вариантом для формирования объективного представления о взаимосвязях финансово-экономических показателей и стратегического развития предприятия. ЗДЕСЬ ПОВТОРИТЬ ВЫВОДЫ САМЫЕ ВАЖНЫЕ Список литературыИшханян М.В., Карпенко Н.В. Эконометрика. Часть 1. Парная регрессия: Учебное пособие. – М.: МГУПС (МИИТ), 2016. – 117 с. Милевский А.С. Высшая математика. Часть 7. Эконометрика: конспект лекций. М.: МИИТ, 2011. – 123 c. Практикум по эконометрике: Учеб. Пособие / И. И. Елисеева, С. В. Курышева, Н. М. Гордеенко и др.; Под ред. И.И. Елисеевой. - М.: Финансы и статистика, 2003. Эконометрика: Учебник / И. И. Елисеева, С. В. Курышева, Т.В. Костеева и др.; под ред. И.И. Елисеевой. - 2-е изд., перераб. и доп. - М.: Финансы и статистика, 2005. Бородич С.А. Эконометрика / Учебное пособие для ВУЗов. – Мн.: Новое знание, 2004. 1 2 | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||

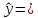 72,57 + 0,88*x + 247,11z
72,57 + 0,88*x + 247,11z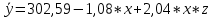
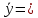 178,75 - 0,04 * x + 0,95 * x * z + 135,59z
178,75 - 0,04 * x + 0,95 * x * z + 135,59z