кр. Институт энергетики и транспортных систем курсоваяработ а
 Скачать 0.91 Mb. Скачать 0.91 Mb.
|
|
ФЕДЕРАЛЬНОЕ ГОСУДАРСТВЕННОЕ АВТОНОМНОЕ ОБРАЗОВАТЕЛЬНОЕ УЧРЕЖДЕНИЕ ВЫСШЕГО ОБРАЗОВАНИЯ «САНКТ-ПЕТЕРБУРГСКИЙ ГОСУДАРСТВЕННЫЙ ПОЛИТЕХНИЧЕСКИЙ УНИВЕРСИТЕТ ПЕТРА ВЕЛИКОГО» ИНСТИТУТ ЭНЕРГЕТИКИ И ТРАНСПОРТНЫХ СИСТЕМ К У Р С О В А Я Р А Б О Т А Расчет стержневой системы на прочность и жесткость при простых видах деформации по дисциплине «Прикладная механика»
Санкт Петербург 2019Содержание Задание …………………………..……………………………………………… 3 1. Расчет стержня на растяжение-сжатие ……………………………………... 6 1.1. Построение эпюры продольной силы …………………………………… 6 1.2. Подбор размеров сечений из условия прочности ……………………… 7 1.3. Определение перемещений сечений ……………………………………… 8 2. Расчет вала на прочность и жесткость …………………………………… 12 2.1. Определение момента на ведущем шкиве ……..……………………...… 13 2.2. Построение эпюры крутящего момента ……………..…………………... 13 2.3. Подбор сечения вала ………………….…………………………………... 13 2.4. Построение эпюры распределения касательных напряжений …………..14 2.5. Построение графика углов поворота сечений ……………...…………... 14 3. Расчёт балки на прочность и жёсткость …………………………………… 16 3.1. Расчет статически определимой балки на прочность ………………… 16 3.1.1. Определение реакции закрепления …..……………………………… 16 3.1.2. Построение эпюры Qy и Mz ………………………………………… 17 3.1.3. Подбор размеров круглого и прямоугольного поперечного сечения 18 3.2. Расчет статически неопределимой балки на прочность ……………… 20 3.2.1. Раскрытие статической неопределимости методом уравнивания постоянных интегрирования приближенного дифференциального уравнения изогнутой оси ………………………………….…………… 20 3.2.2. Построение эпюры Qy и Mz ………………………………………… 22 3.2.3. Определение геометрических характеристик сложного сечения … 23 3.2.4. Определение грузоподъемности из условия прочности …………… 25 3.2.5. Проверка условия жесткости ………………………………………… 25 Заключение …………………………………………………………………… 27 Библиографический список …………………………………………………… 28 ЗаданиеВ рамках курсовой работы требуется провести расчет стержневой системы на прочность и жесткость при простых видах деформации: 1. Расчет стержня на растяжение-сжатие 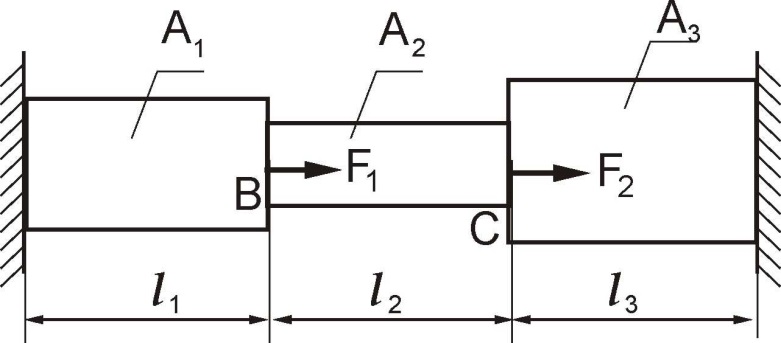
Принять модуль Юнга E = 2∙1011 Па, допускаемое напряжение [] = 160 МПа, коэффициент линейного расширения = 125·10-7 1/0. Исходные данные:
2. Расчет вала на прочность и жесткость 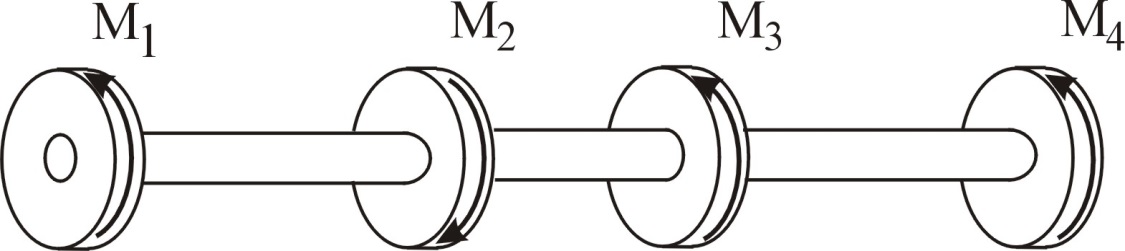 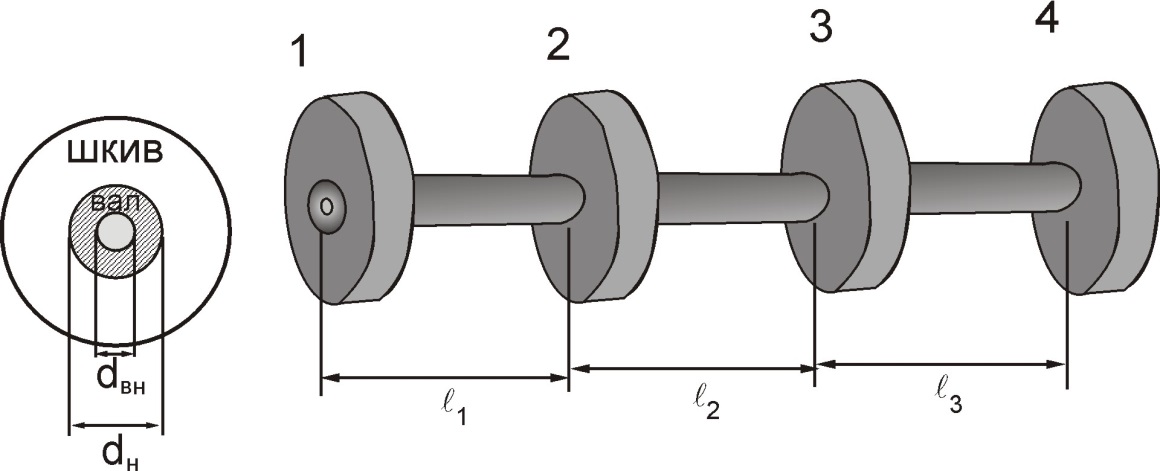
Принять модуль сдвига G = 8∙ 1010 Па, допускаемое напряжение [] = 80 МПа, [] = 1 град/м = 17,5∙ 10-3 рад/м. Исходные данные:
3. Расчет балки на прочность и жесткость 3.1. Статически определимая балка, защемленная одним концом. 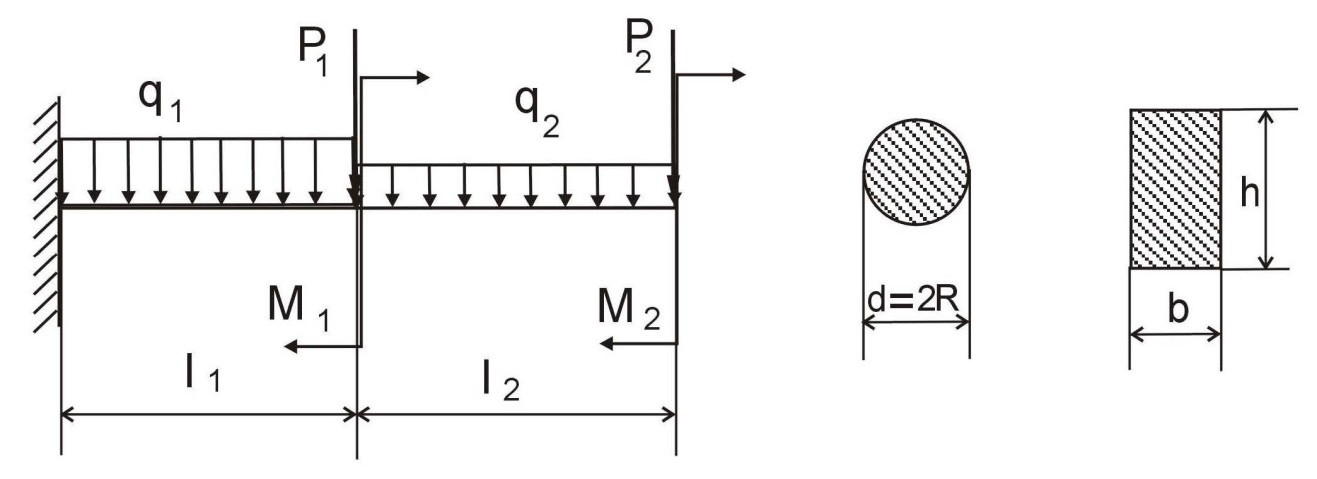 1. Определить реакции закрепления. 2. Построить эпюры Qy и Mz. 3. Подобрать размеры круглого и прямоугольного поперечного сечения, приняв допускаемое напряжение [] = 10 МПа. Исходные данные:
3.2. Статически неопределимая балка. 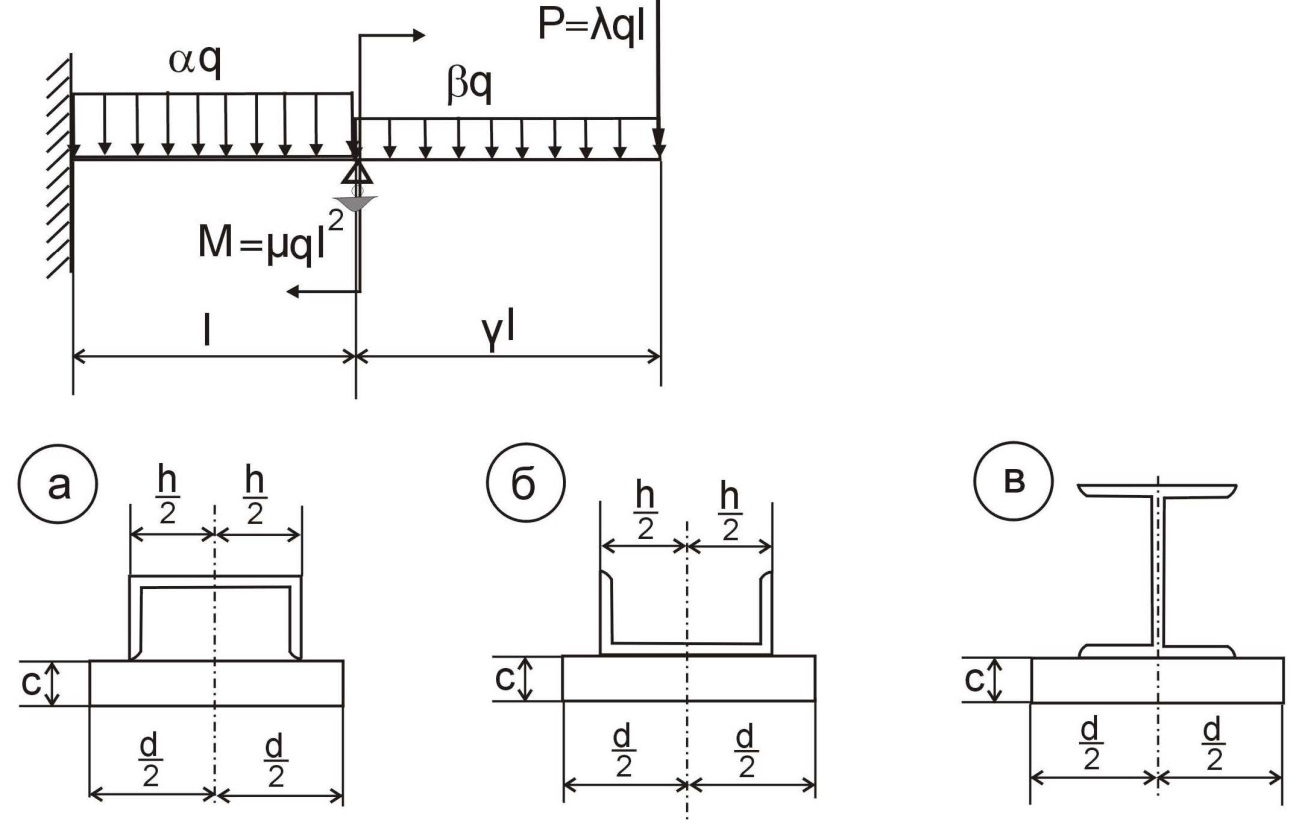 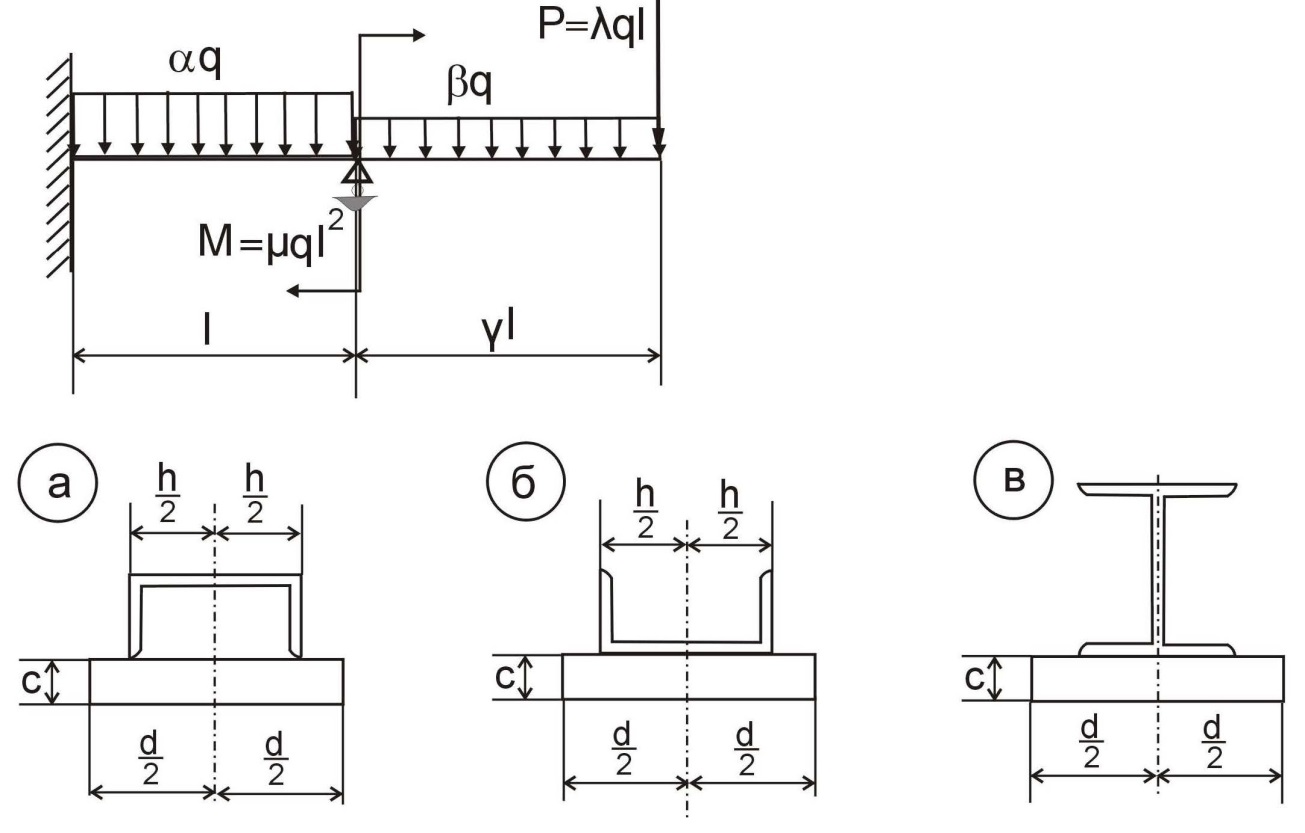
Исходные данные:
Дата получения задания: «___».____________ 20__ г. Руководитель _____________ _Китаева Д.А._ (подпись) (инициалы, фамилия) Задание принял к исполнению _____________ _______________ (подпись студента) (инициалы, фамилия) 1.Расчет стержня на растяжение-сжатие 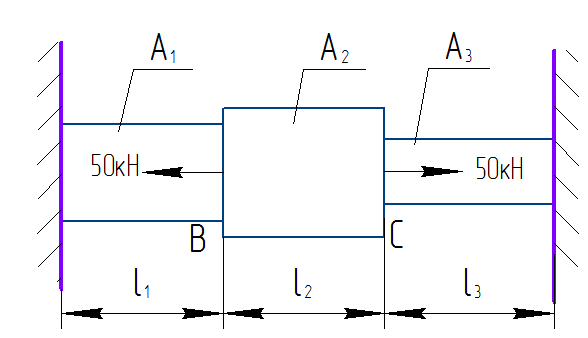 F1= 50кН, F2=50кН, l1=2м, l2=2м, l3=2,1м, А1: А2: А3=1,5:2:1  = 160 МПа = 160 МПаi=2 δ= -0,5мм Е=2∙ 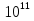 Па ПаА1, А2, А3-?  , ,  -? -?
Выразим продольные усилия через внешние силы:  , ,  , ,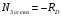 Запишем уравнение равновесия:   Т.к. имеем одно уравнение и два неизвестных, система один раз статически неопределима. Дополнительное уравнение – уравнение совместности перемещений:  . .Это уравнение не содержит в явном виде неизвестных реакций RA и RD , поэтому воспользуемся законом Гука:   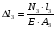      Получаем систему:   Решив ее, находим:  , , 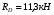 Определим продольные усилия: 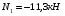 , , , ,
Запишем условия прочности для отдельных участков и подберем их сечения, сохраняя заданные соотношения между ними:   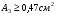  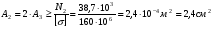   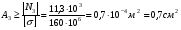 Принимая A3 ≥ 1,2см2 , получим: 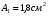 , ,  , ,  . .Тогда:    Несмотря на то, что  , такой перегруз допустим, т.к. он не превышает 5% : , такой перегруз допустим, т.к. он не превышает 5% :  1.3. Определение перемещений сечения  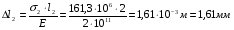 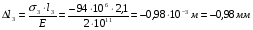   , , Сечение В перемещается влево, сечение С перемещается вправо. 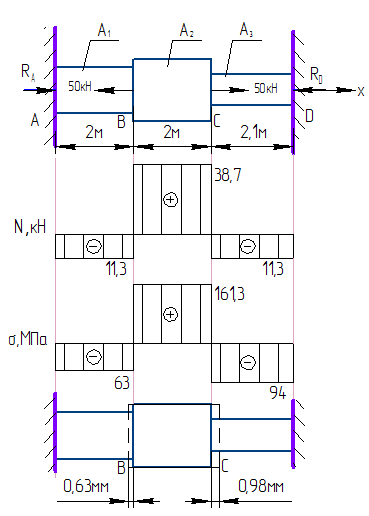 Пусть стержень изготовлен неточно на 2ом участке – короче, чем нужно, на величину δ = -0,5мм. Тогда в нем при установке (сборке) возникнут внутренние усилия (напряжения) даже при отсутствии внешних сил. Из уравнения равновесия следует: 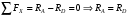 . Методом сечений устанавливаем, что: . Методом сечений устанавливаем, что: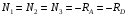 . После подстановки физических уравнений в уравнение совместности получаем: . После подстановки физических уравнений в уравнение совместности получаем:     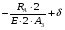    Тогда  Найдем напряжения и построим эпюру:  , , 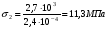 , , 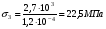 . .Проверим выполнение условия совместности:  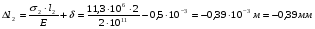    , ,  Сечение В перемещается вправо, сечение С перемещается влево. 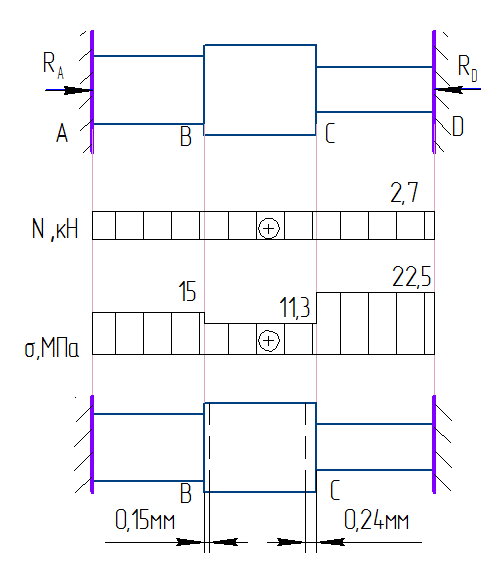 2.Расчет вала на прочность и жесткость с = 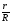 = 0,8 = 0,8 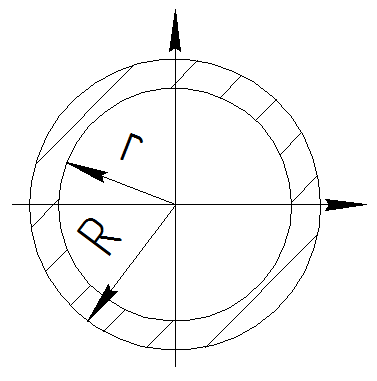 l1=2м, l2=1м, l3=1,6м, М1=10кН∙м, М3=20кН∙м, М4=30кН∙м, [τ]= 80МПа [θ]= 1град/м=17,5∙  рад/м рад/м G=8∙  Па ПаR, r -? Гр. φ -?  На вале закреплено 4 шкива, второй шкив – ведущий, три остальные - ведомые. Направление внешнего момента на ведущем шкиве  противоположно направлению тормозящих моментов на ведомых шкивах противоположно направлению тормозящих моментов на ведомых шкивах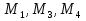 , значения которых заданы. После преодоления начальной силы трения покоя все шкивы начинают вращаться в одну сторону с постоянной угловой скоростью. При этом все внешние моменты, действующие на вал, находятся в равновесии. , значения которых заданы. После преодоления начальной силы трения покоя все шкивы начинают вращаться в одну сторону с постоянной угловой скоростью. При этом все внешние моменты, действующие на вал, находятся в равновесии.2.1. Определение момента на ведущем шкиве Определим момент на ведущем шкиве 2 из уравнения равновесия:   2.2. Построение эпюры крутящего момента Эпюру крутящего момента Мx построим методом сечений, используя правило знаков. На каждом из трех участков вала выберем произвольное сечение и рассмотрим внешние моменты с одной стороны от сечения:     Выбираем опасный участок - тот, где крутящий момент принимает наибольшее значение:  . .2.3. Подбор сечения вала ▪ По условию прочности:  , ,  , ,  = = ▪ По условию жесткости:  , I , I , ,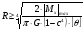 = = Выбираем значение R, удовлетворяющее обоим неравенствам:  тогда r тогда r  . .2.4. Построение эпюры распределения касательных напряжений Вычислим напряжение на наружной и внутренней поверхности стержня в поперечном сечении на опасном участке: 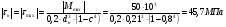  , где , где 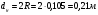 . . 2.5. Построение графика углов поворота сечений Найдем углы закручивания участков вала: 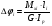 , где I , где I 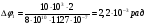   Построим график углов поворота сечений относительно первого сечения, условно считая φ1=0: φ2= φ1 + Δ φ1 = 2,2∙10-3рад φ3= φ2 + Δ φ2 = 2,2∙10-3 - 5,5∙10-3= -3,3∙10-3рад φ4= φ3 + Δ φ3 = -3,3∙10-3 – 5,3∙10-3= -8,6∙10-3рад  3. Расчет балки на прочность и жесткость 3.1. Расчет статически определимой балки на прочность  М=10кН∙м  q=10кН/м Р=50кН [σ] = 10МПа l1=2,4м, l2=1,5м h/b=2,2  h, b, 
 Из уравнения равновесия:  , ,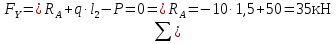 , , 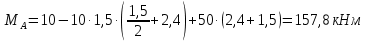 . .3.1.2. Построение эпюр 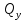 и и  Разобьем балку на два участка. На первом участке будем рассматривать все внешние силы слева от произвольного сечения, находящегося на расстоянии  от заделки: от заделки:  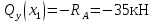 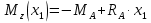 => => 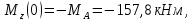  . .На втором участке будем рассматривать все внешние силы справа от произвольного сечения, находящегося на расстоянии  от свободного конца: от свободного конца: 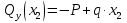 => => 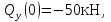   => =>    3.1.3. Подбор размеров круглого и прямоугольного поперечного сечения Подберем из условия прочности  круглое и прямоугольное сечение для балки. круглое и прямоугольное сечение для балки. ▪ для круглого сечения: 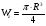 , ,  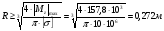 Принимаем  , тогда , тогда  ▪ для прямоугольного сечения:  , ,  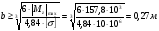 Принимаем 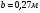 , , , тогда , тогда  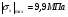 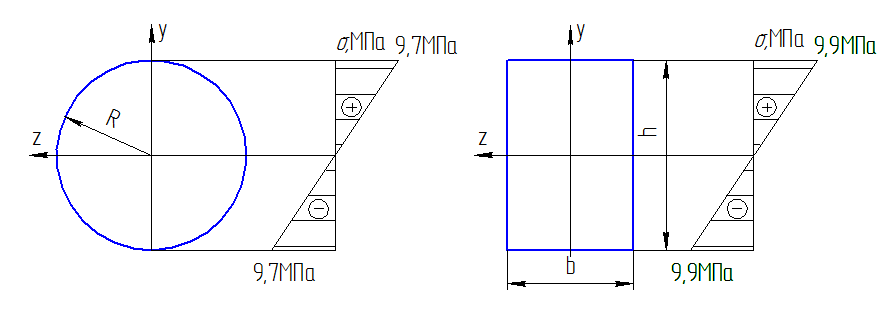 3.2. Расчет статически неопределимой балки на прочность [σ] = 160МПа l=2м с=2см, d=12см, N10  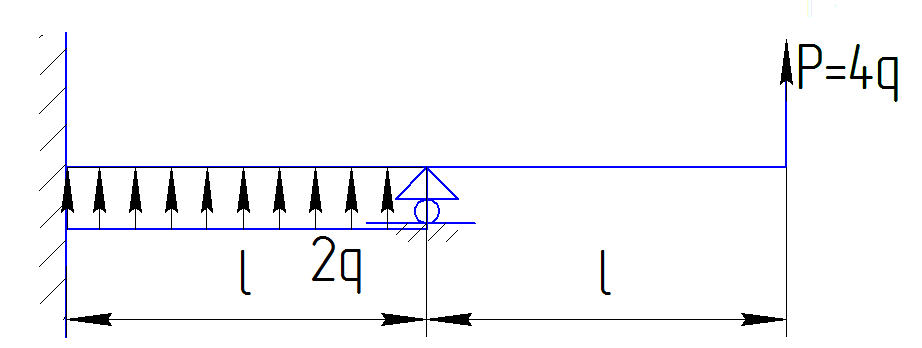 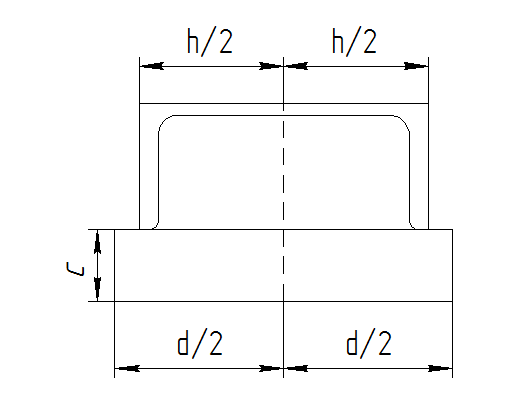 3.2.1. Раскрытие статической неопределимости Раскроем статическую неопределимость балки методом уравнивания постоянных интегрирования приближенного дифференциального уравнения изогнутой оси.  Уравнения равновесия:    Балка один раз статически неопределима. Для определения реакций составим дифференциальное уравнение, которое запишем по двум участкам балки.  На первом участке  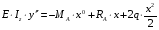   На втором участке   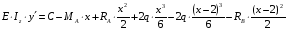 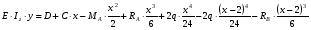 Условия закрепления: у(0)=0, у'(0)=0 (в сечении х=0 находится заделка), у(2)=0 (в сечении х=2 находится шарнирная опора). Отсюда: С=0, D=0. Получаем недостающее уравнение и решаем систему из трех уравнений с тремя неизвестными:     Получаем:   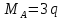 . .3.2.2. Построение эпюр  и и  Разобьем балку на два участка. На первом участке рассмотрим все внешние силы слева от произвольного сечения, находящегося на расстоянии  от заделки от заделки : : 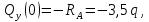   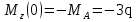 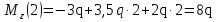 Для второго участка  - расстояние от правого свободного конца балки - расстояние от правого свободного конца балки  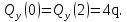   3.2.3.Определение геометрических характеристик сложного сечения Сечение состоит из двух частей: ▪ швеллера N10:  =10,9 =10,9 , ,  =20,4 =20,4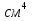 ▪ прямоугольника:  =d∙c=12∙2=24 =d∙c=12∙2=24 , , 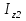 = = =8 =8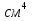  Определим положение центра тяжести составного сечения. Он находится на оси симметрии – оси у. Координату 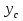 найдем относительно некоторой начальной оси найдем относительно некоторой начальной оси  : : Определение момента инерции: 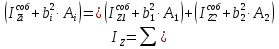  Определение момента сопротивления:  3.2.4.Определение грузоподъемности из условия прочности  3.2.5. Проверка условия жесткости Определим два характерных прогиба: наибольший прогиб в пролете 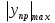 (здесь это первый участок) и наибольший прогиб на консоли (здесь это первый участок) и наибольший прогиб на консоли 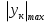 (здесь это второй участок). (здесь это второй участок).Чтобы определить 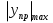 , найдем точку экстремума функции у, решив уравнение , найдем точку экстремума функции у, решив уравнение  на первом участке: на первом участке:  Корень этого уравнения х=1,36м принадлежит отрезку  . Таким образом, . Таким образом,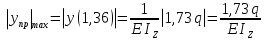 Вычислим теперь  . Он равен прогибу на конце консоли: . Он равен прогибу на конце консоли:     Выбираем  Тогда:  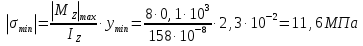  Вычислим наибольшие прогибы:    ЗаключениеВ курсовой работе определены
 , ,  , ,  . .
размер сечения dн, dв из условия прочности / жесткости:  r= r= , ,dн  dв=2r= dв=2r= . .
для статически определимой балки:
для статически неопределимой балки:
 , , , ,  . .
Библиографический список:1. Чернышева Н.В. Прикладная механика. – СПб.: Изд-во Политехн. ун-та, 2016. 2. Феодосьев В.И. Сопротивление материалов. – М.: Изд-во МГТУ им. Н.Э. Баумана, 2016. 3. Павлов П.А., Паршин Л.К., Мельников Б.Е., Шерстнев В.А. Сопротивление материалов. – СПб.: Лань, 2007. 4. Беляев Н.М. Сопротивление материалов. – М.: Альянс, 2014. 5. Ицкович Г.М., Минин Л.С., Винокуров А.И. Руководство к решению задач по сопротивлению материалов. – М.: Высшая школа, 2001. |

 ,
, .
.
 .
.
 .
.