интеграл+лебега. Интеграл Лебега
 Скачать 1.07 Mb. Скачать 1.07 Mb.
|
|
6. Примеры 1) Вычислить интеграл Лебега от функции Строим срезку  N, f(x) N, fN(x) = f(x), f(x) N. x = 1 + 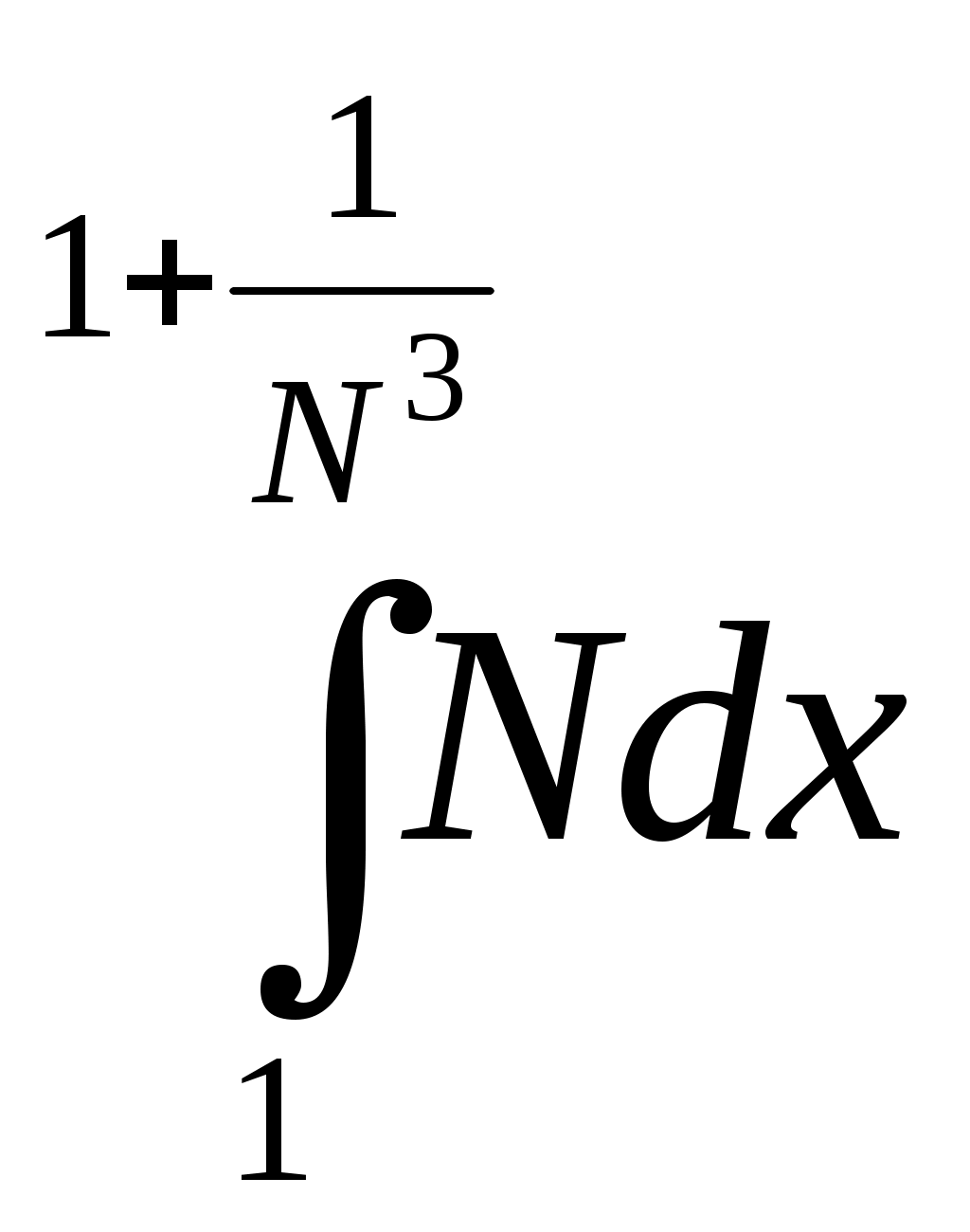 + + 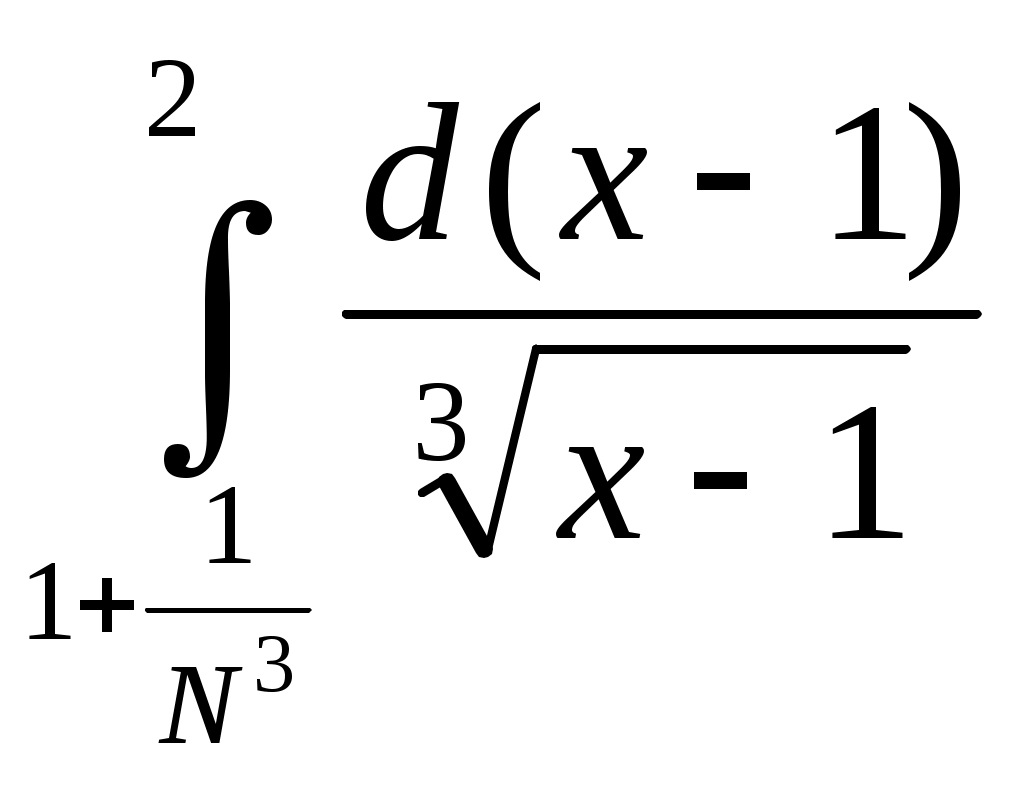 = Nx = Nx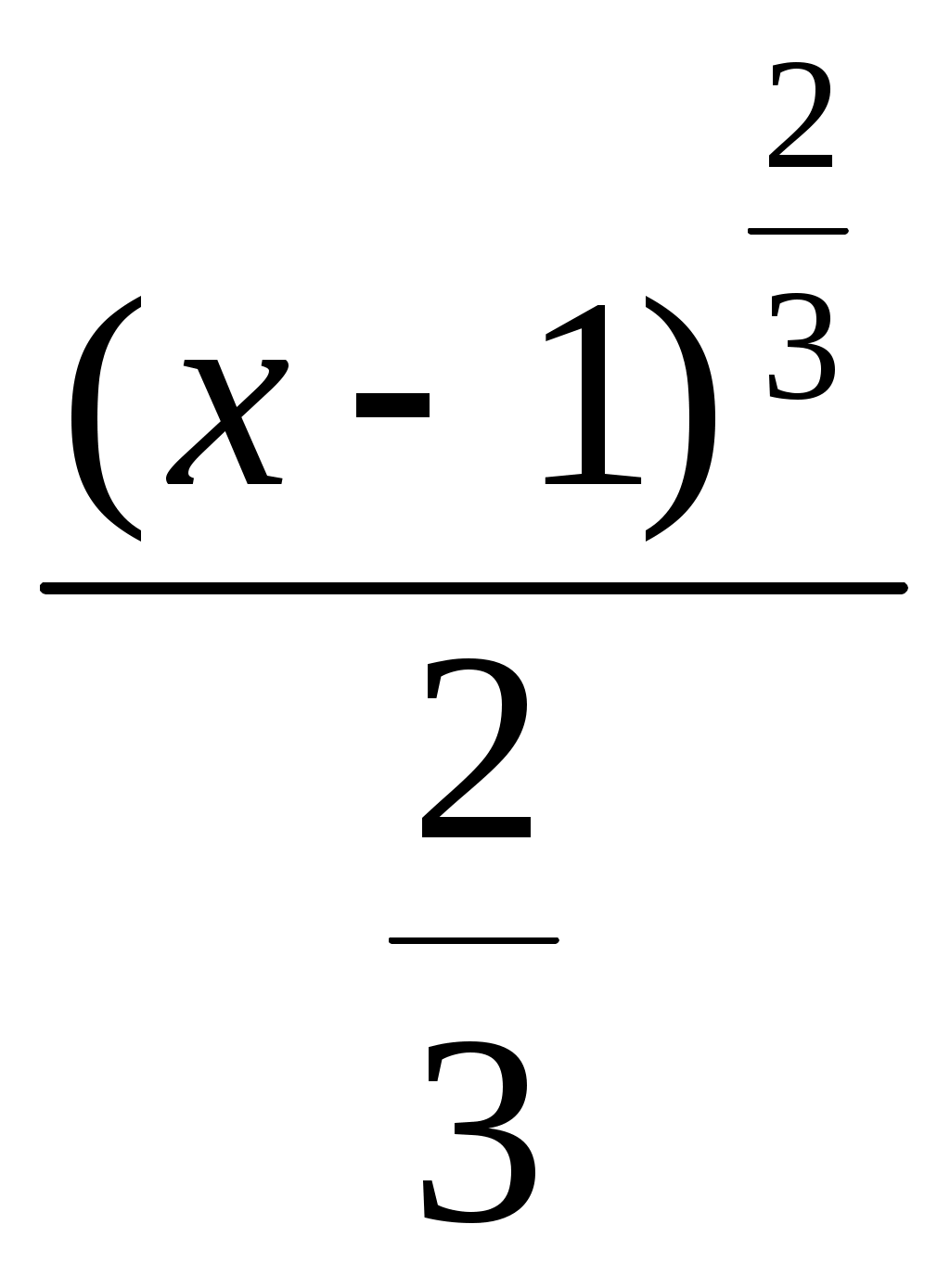 - (L) 2) Суммируемы ли функции f(x) = Строим срезку x = 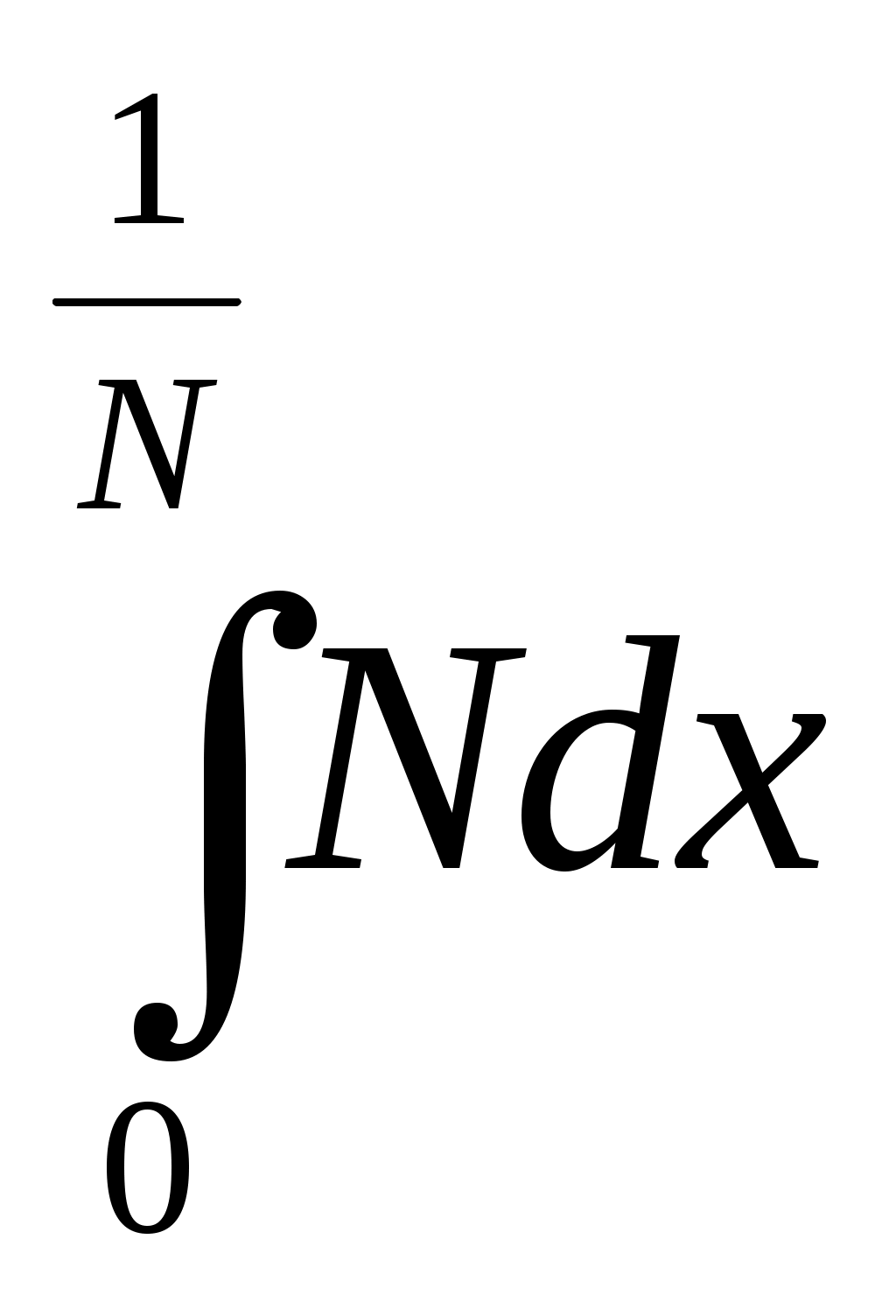 + + 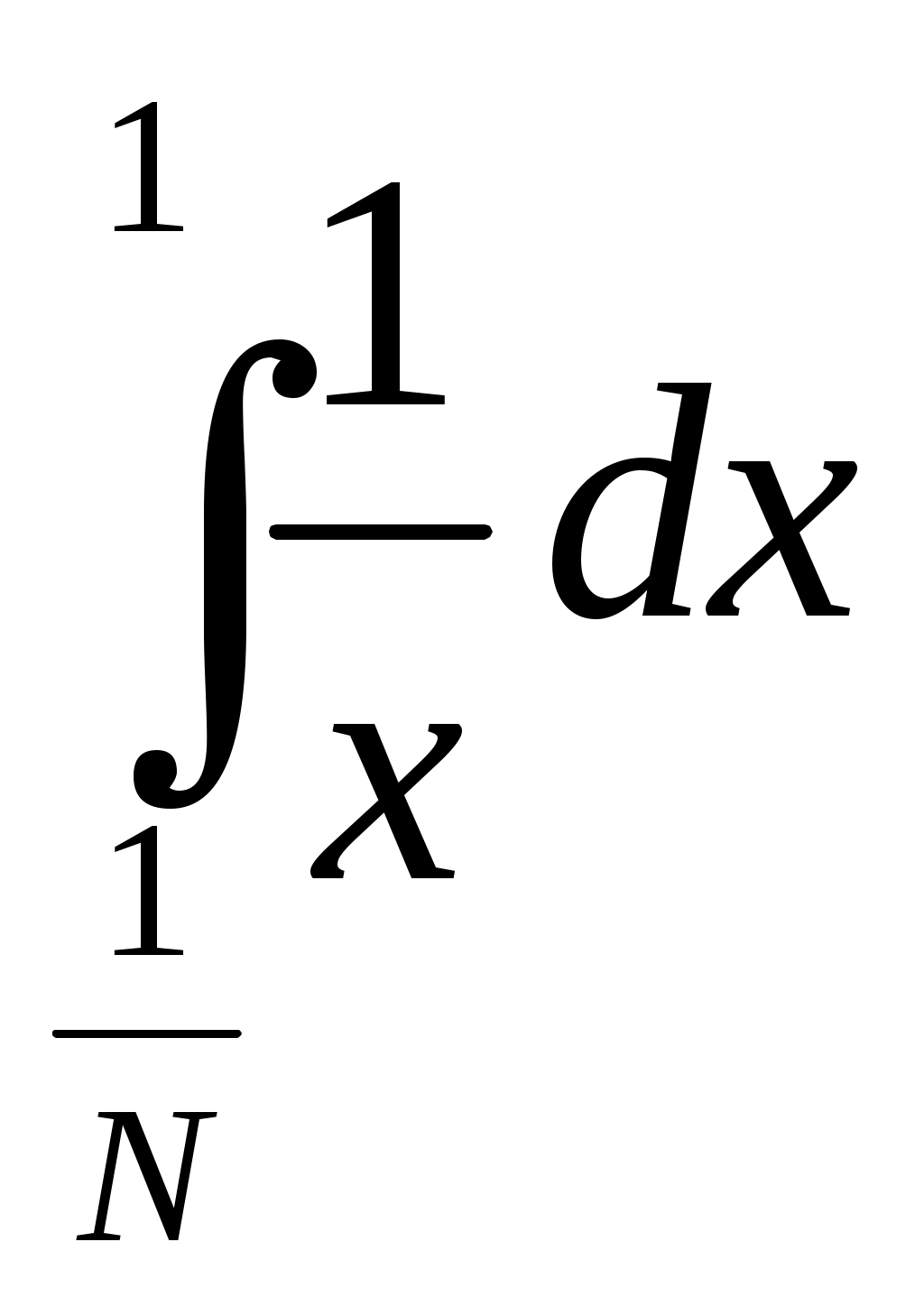 = = значит функция f(x) = f(x) = Строим срезку x = 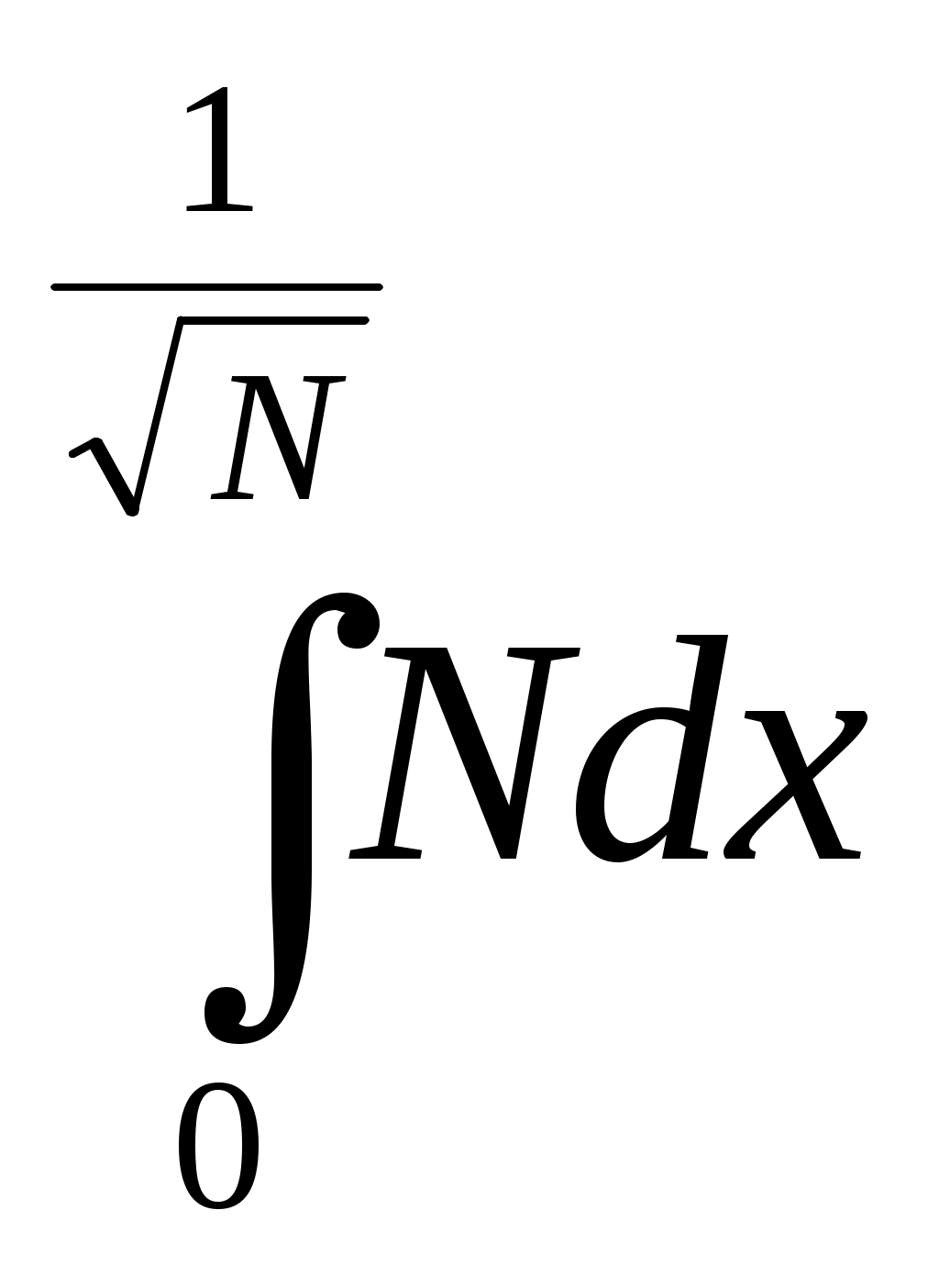 + + 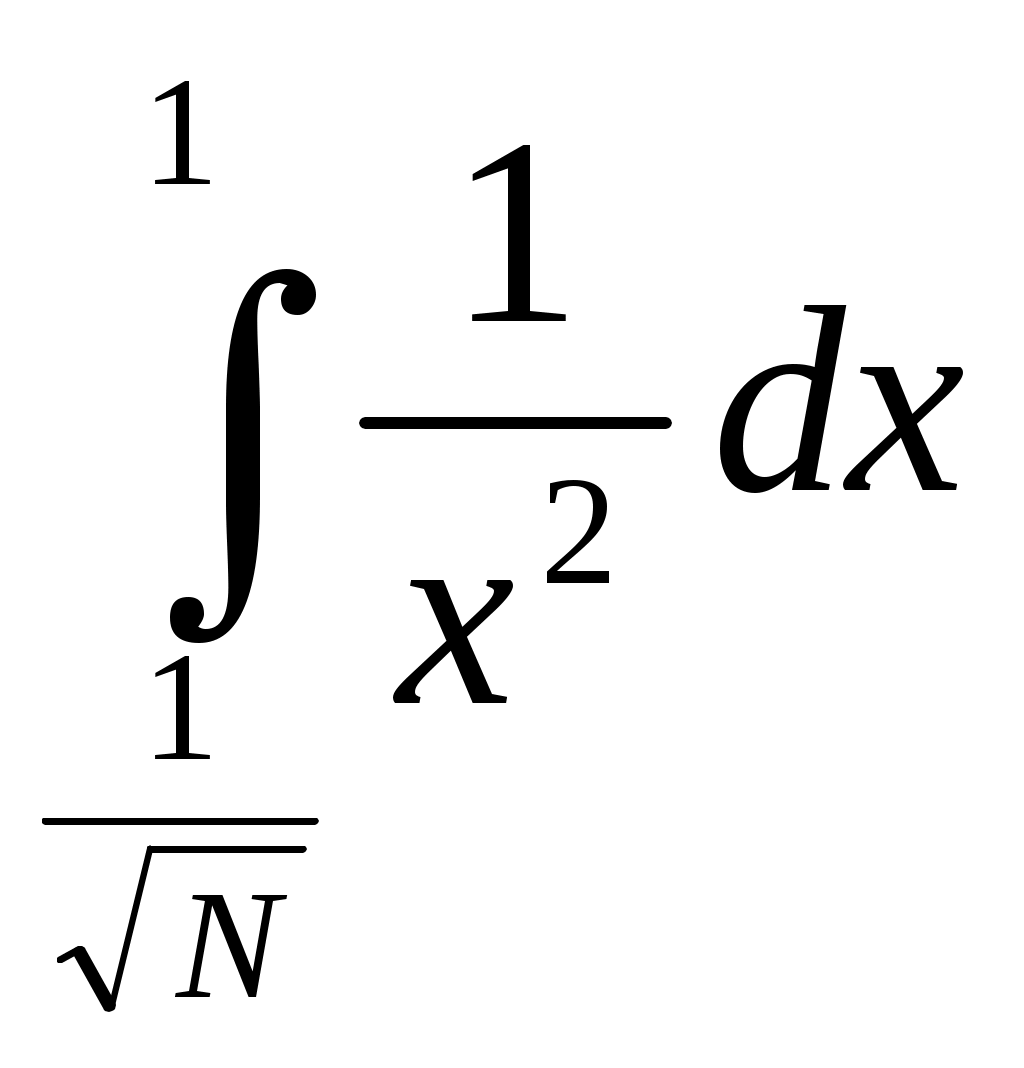 = = = 2 значит функция f(x) = 3) Суммируема ли функция f(x) = 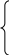 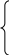 0 , x 0 Строим срезку N = x = (L) 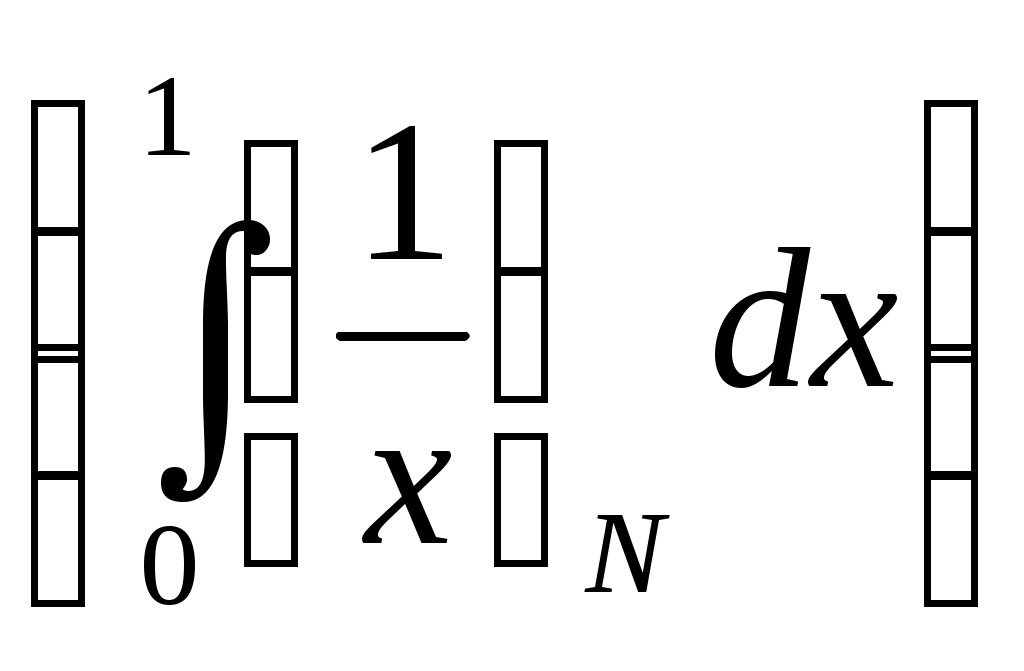 = = 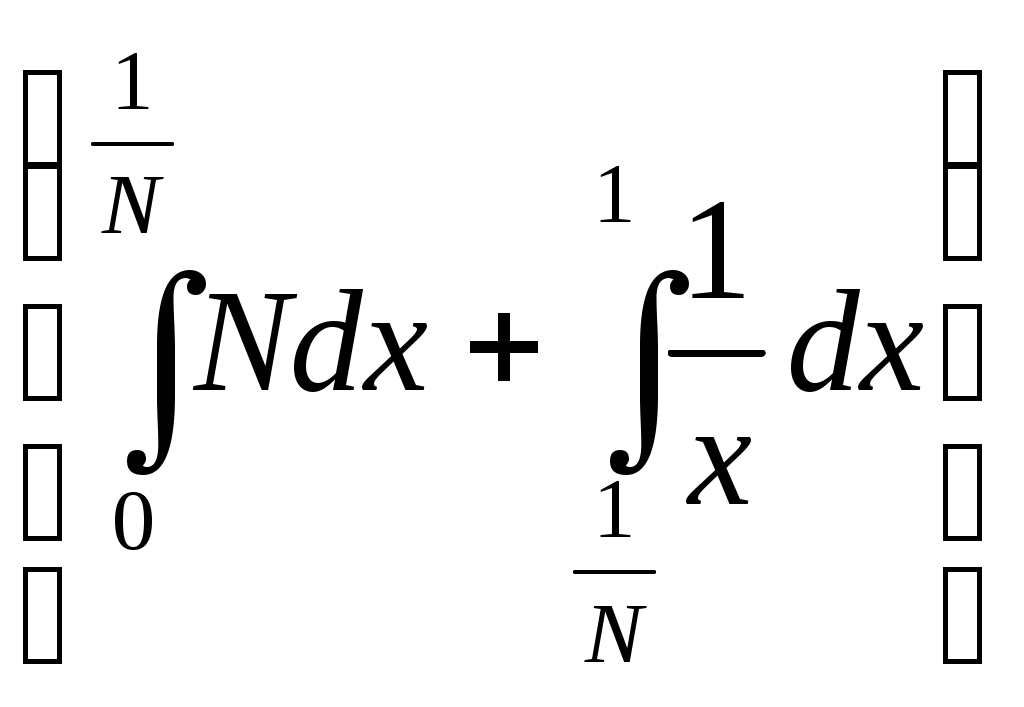 = = 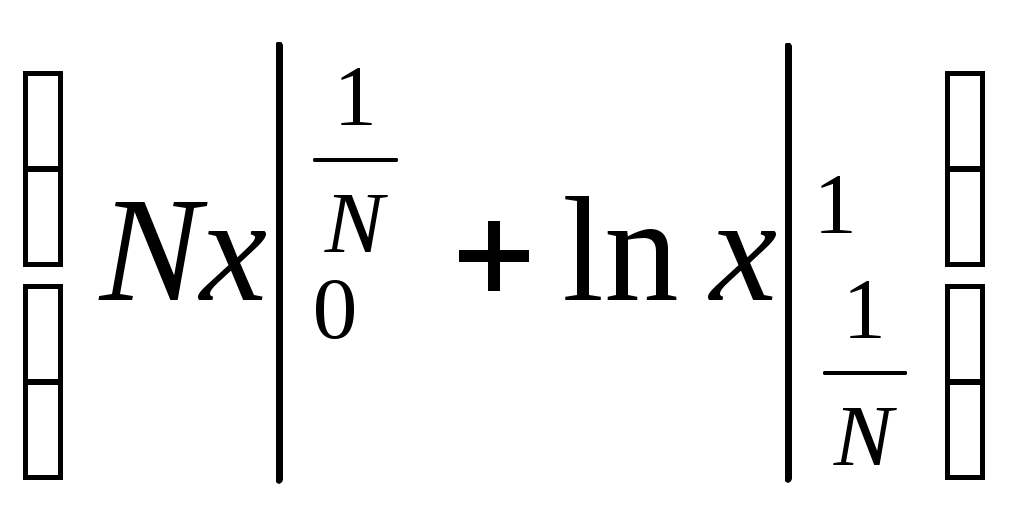 = = = Строим срезку N = x = (L) 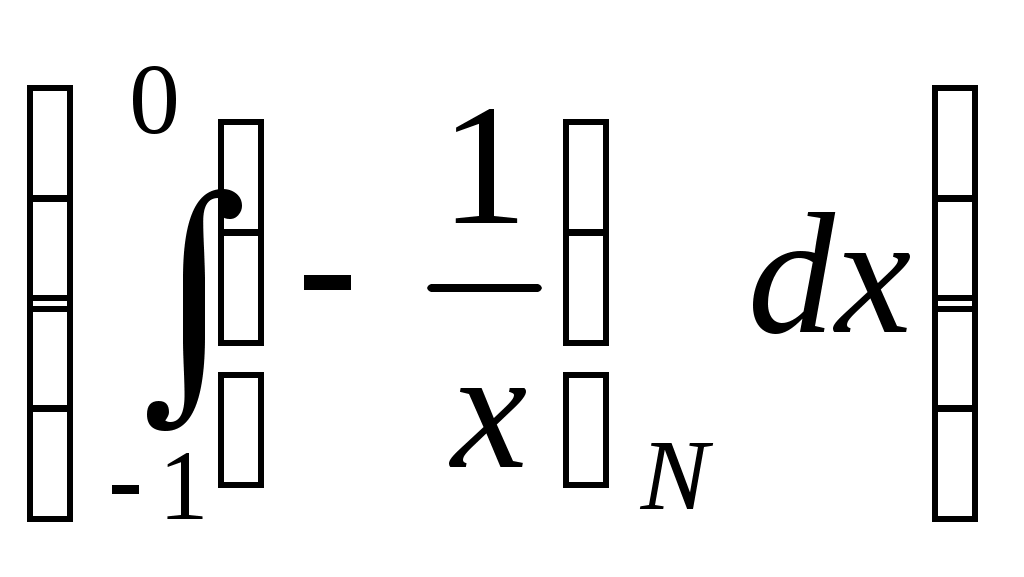 = = 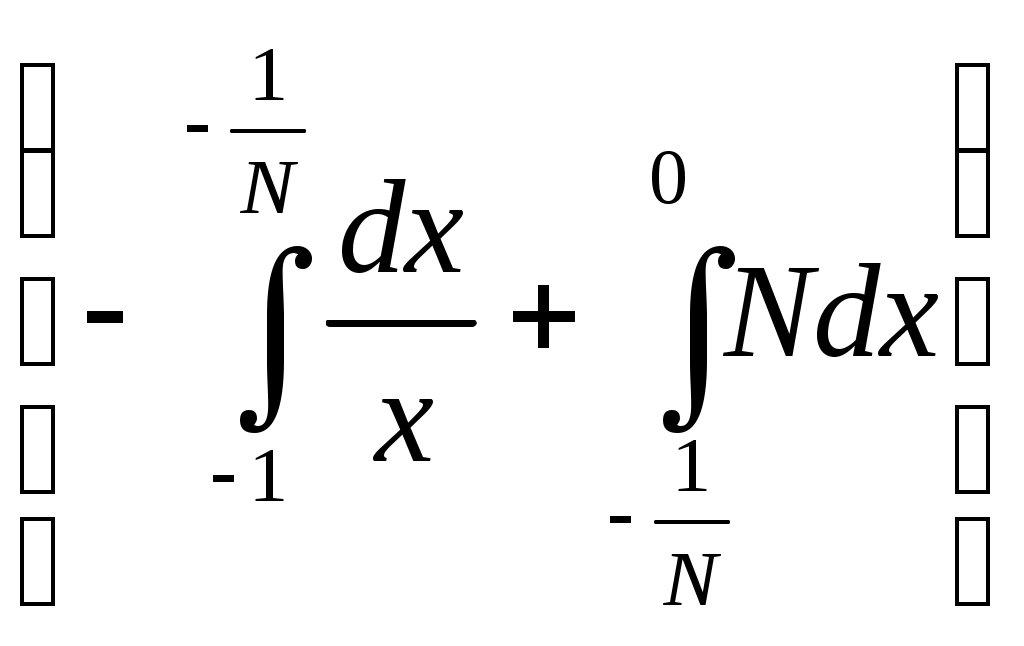 = = 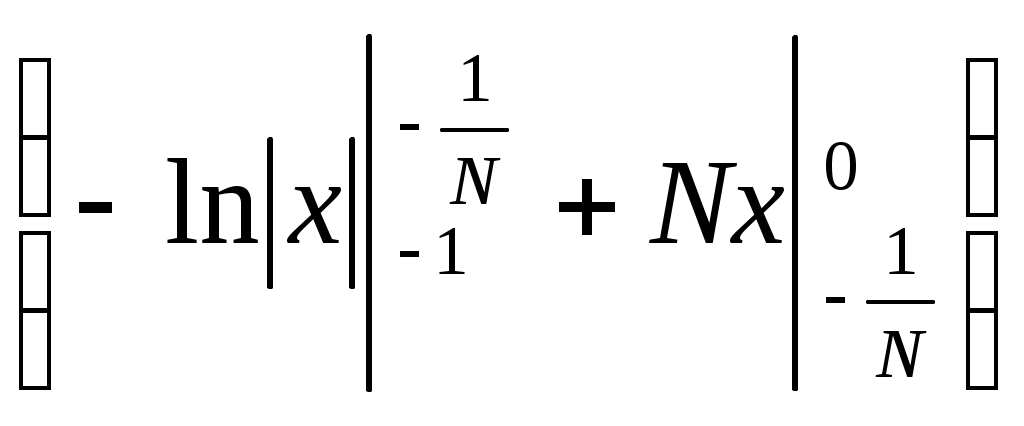 = = = значит функция f(x) = 4) Суммируема ли функция f(x) =   1, x = 2 Строим срезку x = 2 + (L) 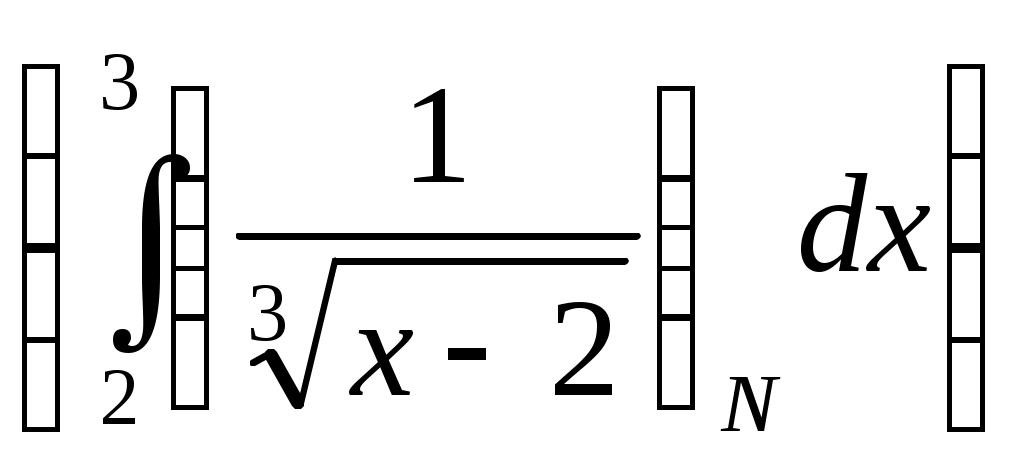 = = 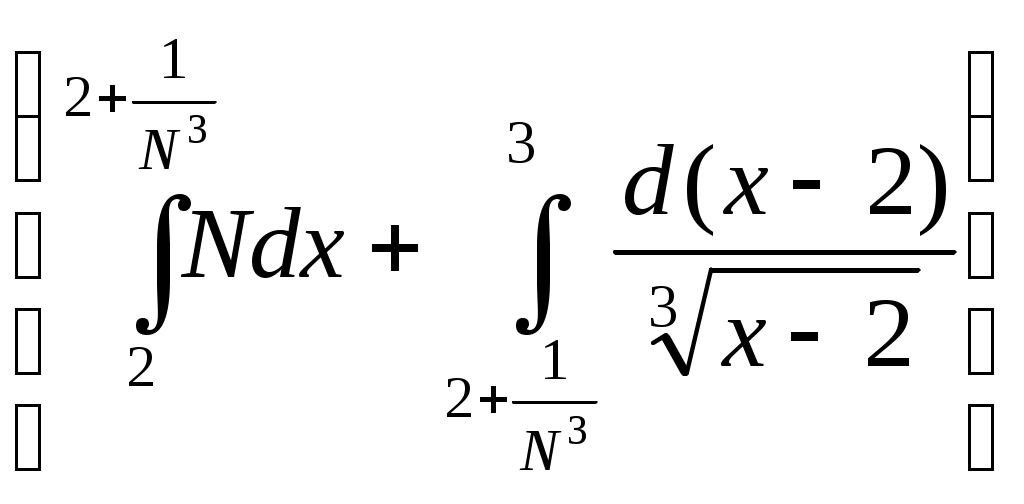 = = = 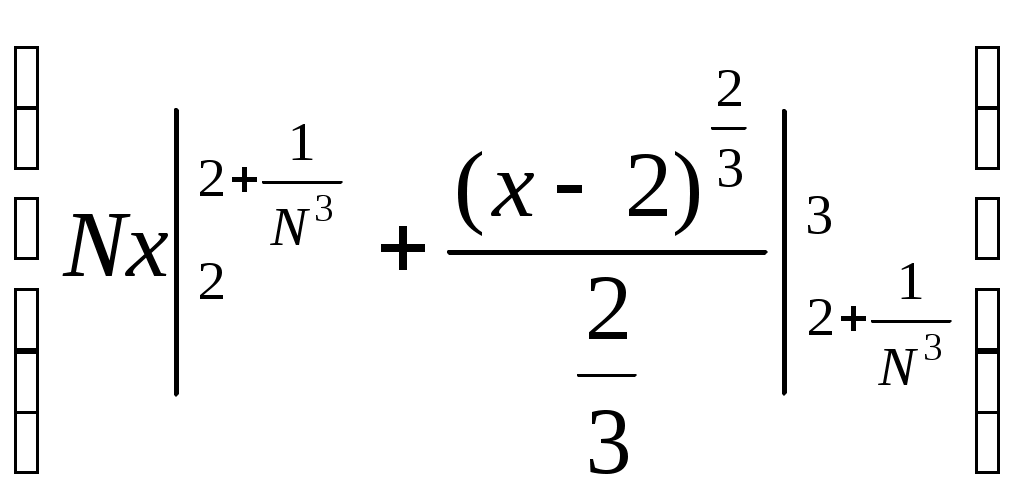 = = 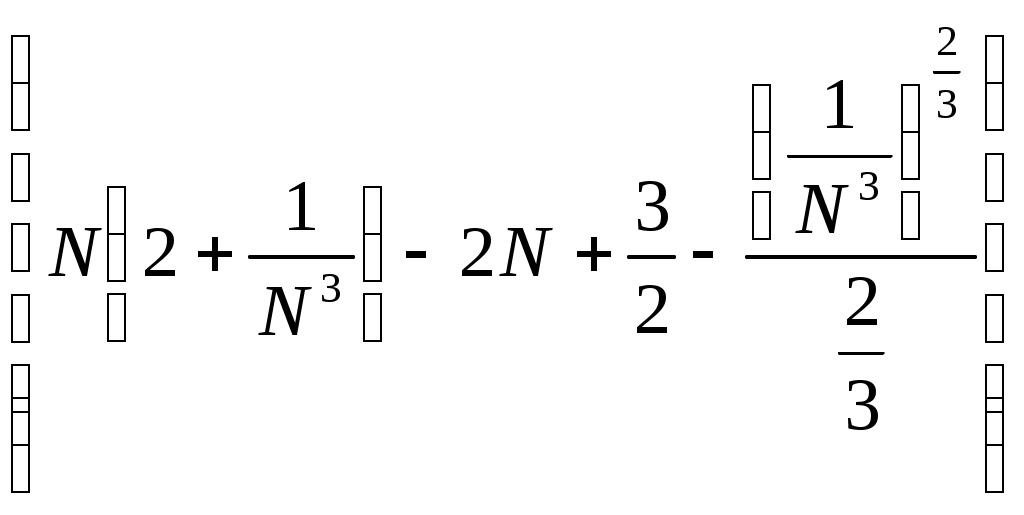 = = = Строим срезку x = 2 - (L) 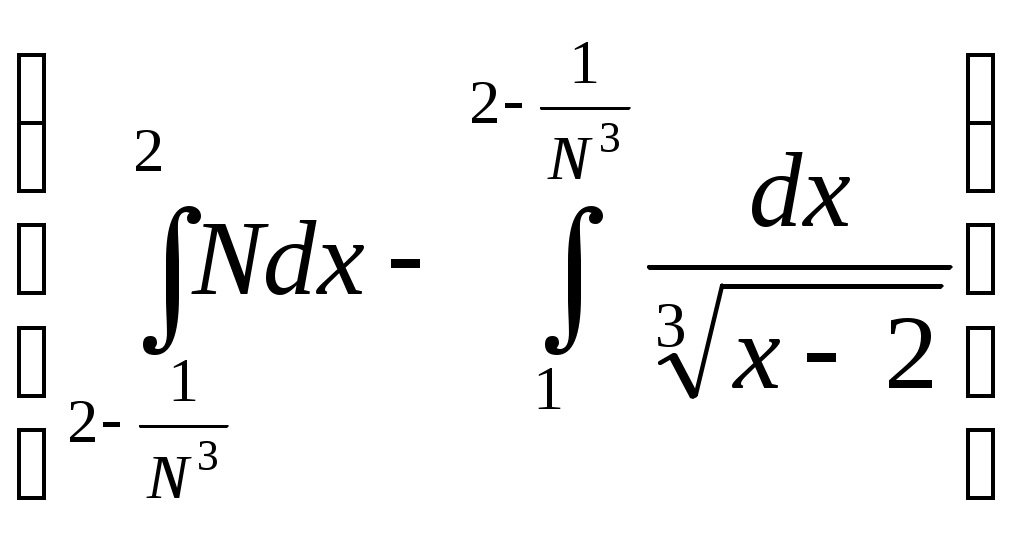 = = 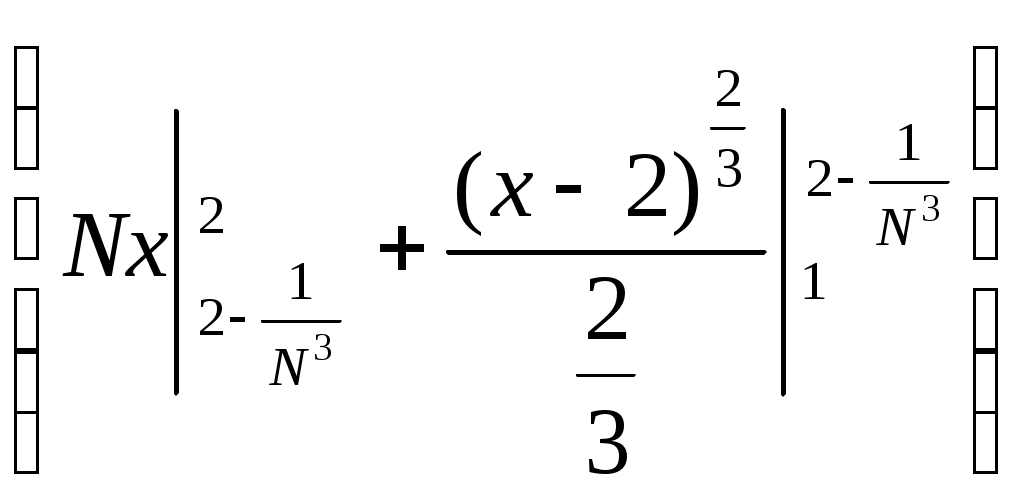 = = 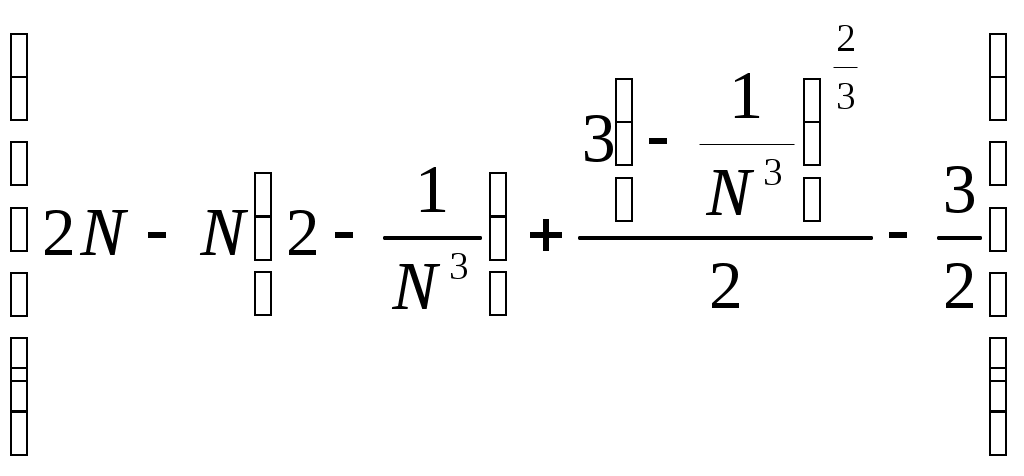 = = функция f(x) суммируема на [1; 3]. 7. Литература 1) Колмогоров, Фомин «Элементы функционального анализа». 2) Натансон И. П. «Теория функций вещественной переменной», С-П, 1999. 3) Очан «Сборник задач по математическому анализу». |
