интеграл+лебега. Интеграл Лебега
 Скачать 1.07 Mb. Скачать 1.07 Mb.
|
|
3. Основные свойства интеграла В этом параграфе мы установим ряд свойств интеграла от ограниченной измеримой функции. Теорема 1. Если измеримая функция f(x) на измеримом множестве Е удовлетворяет неравенствам af(x) b, то a mE Это теорема обычно называется теоремой о среднем. Доказательство. Пусть n натуральное число. Если мы положим A = a - то окажется, что Af(x) B, и суммы Лебега можно будет составлять, дробя сегмент [А, В]. Но еслиAykB, то, очевидно, A или, что то же самое, A mE s B mE, откуда и в пределе В силу произвольности числа n, теорема доказана. Из этой теоремы вытекает несколько простых следствий. Следствие 1. Если функция f(x) постоянна на измеримом множестве Е и f(x) = с, то Следствие 2. Если функция f(x) не отрицательна (не положительна), то таков же и ее интеграл. Следствие 3. Если тЕ = 0, то для любой ограниченной функции f(x), заданной на множестве Е, будет Теорема 2. Пусть на измеримом множестве Е задана измеримая ограниченная функция f(x). Если множество Е есть сумма конечного числа или счетного множества попарно не пересекающихся измеримых множеств E = то Свойство интеграла, выражаемое этой теоремой, называется его полной аддитивностью. Доказательство. Рассмотрим сначала простейший случай, когда число слагаемых равно двум Е = Если на множестве Е A < f(x) < B и мы, раздробив сегмент [А, В] точками у0, y1, , уn, составим множества ek = E(yk f yk+1), ek’= E’(yk f yk+1), ek’’= E’’(yk f yk+1), то, очевидно, будем иметь ek = ek’ + ek’’ (ek’ek’’ = 0), откуда н в пределе, при 0, Итак, теорема доказана для случая двух слагаемых множеств. Пользуясь методом математической индукции, мы легко распространим теорему на случай любого конечного числа слагаемых множеств. Остается рассмотреть случай, когда E = В этом случае так что при nбудет Заметив это, положим Так как для конечного числа слагаемых множеств теорема уже доказана, то В силу теоремы о среднем A mRn а в силу (*) мера mRn множества Rn стремится к нулю с возрастанием n, откуда ясно, что Но это и означает, что Из этой теоремы вытекает ряд следствий. Следствие 1. Если измеримые ограниченные функции f(x) и g(x), заданные на множестве Е, эквивалентны между собой, то Действительно, если А = Е(fg), B = E(f = g), то mA = 0 и На множестве же В обе функции тождественны и Остается сложить это равенство с предыдущим. В частности, интеграл от функции, эквивалентной нулю, равен нулю. Само собою разумеется, что последнее утверждение необратимо. Например, если f(x) задана на сегменте [-1, +1], так:  1 при x 0, 1 при x 0, f(x) = -1 при x 0, то хотя функция f(x) и не эквивалентна нулю. Однако справедливо Следствие 2. Если интеграл от неотрицательной измеримой ограниченной функции f(x) равен нулю то эта функция эквивалентна нулю. В самом деле, легко видеть, что E(f0) = Если бы f(x) не была эквивалентна нулю, то необходимо нашлось бы такое n0, что mE Полагая A = E мы имели бы, что и, складывая эти неравенства, мы получили бы что противоречит условию. Теорема 3. Если на измеримом множестве Q заданы две измеримые ограниченные функции f(x) и F(x), то Теорема 4. Если на измеримом множестве Е задана измеримая ограниченная функция f(x) и с есть конечная постоянная, то Следствие. Если f(x) и F(х) измеримы и ограничены на множестве Е, то Теорема 5. Пусть f(x) и F(х) измеримы и ограничены на измеримом множестве Е. Если f(x) F(x), то Действительно, функция F(x)—f(x) не отрицательна, так что Теорема 6. Если функция f(x) измерима и ограничена на измеримом множестве E, то 4. Предельный переход под знаком интеграла Здесь мы рассмотрим следующий вопрос: пусть на измеримом множестве E задана последовательность измеримых ограниченных функций f1(x), f2(x), f3(x), , fn(x), которая в каком-нибудь смысле (везде, почти везде, по мере) сходится к измеримой ограниченной функции F(x). Спрашивается, будет ли справедливо соотношение Если (1) верно, то говорят, что допустим предельный переход под знаком интеграла. Легко видеть, что, вообще говоря, это не так. Например, если функции fn(x) определены в сегменте [0, 1] следующим образом: 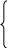 n при x n при x fn(x) = 0 при x то при всяком x [0, 1] будет и этот интеграл не стремится к нулю. Поэтому естественно поставить вопрос о тех дополнительных ограничениях, которые нужно наложить на функцию fn(x), чтобы равенство (1) все же имело место. Мы ограничимся доказательством следующей теоремы. Теорема (А. Лебег). Пусть на измеримом множестве Е задана последовательность f1(x), f2(x), f3(x), измеримых ограниченных функций, сходящаяся по мере к измеримой ограниченной функции F(х) fn(x) F(x). Если существует постоянная К, такая, что при всех п и лри всех х то |
