Иррациональные уравнения и их системы. Иррациональные уравнения и их системы
 Скачать 75.88 Kb. Скачать 75.88 Kb.
|
|
Тема: Иррациональные уравнения и их системы. Иррациональным называется уравнение, в котором неизвестное (переменная) содержится под знаком корня или под знаком операции возведения в рациональную (дробную) степень. Для решения иррациональных уравнений обычно используются следующие приемы: 1)возведение в соответствующую степень обе части уравнения; 2) введение новой переменной; 3) сведение к системе уравнений; 4) применение свойств функций, входящих в уравнение. При решении иррациональных уравнений необходима проверка всех найденных корней путем их подстановки в исходное уравнение или нахождение ОДЗ и следующий анализ корней (при решении методом приведения к равносильной смешанной системе уравнений и неравенств необходимость в этом отпадает). Простейшим иррациональным уравнением является уравнение вида: при решении которого важную роль играет четность или нечетность n. Если n- нечетное, то данное уравнение равносильно уравнению Если n - четное, то, так как корень считается арифметическим, необходимо учитывать ОДЗ (область допустимых значений): 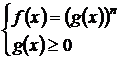 . .Пример 1. Решить уравнение 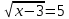 . .Решение. Так как n=2 - четное, то обе части уравнения возводим во 2ю степень: 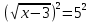  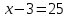 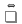 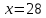 Ответ:_28_Пример_2_.'>Ответ: 28 Пример 2. Решить уравнение Решение. Так как в данном примере n=3 - нечетное, то после возведения обеих частей уравнения в третью степень получим равносильное данному уравнение: 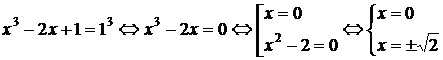 . .Ответ: Пример 3. Решить уравнение Решение. Так как n=2 - четное, то исходное уравнение равносильно системе: 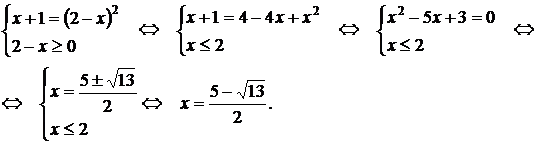 Ответ: Уравнения вида n – нечетное 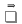 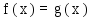 n - четное 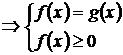 или или 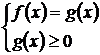 . .Пример 4. Решить уравнение: 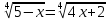 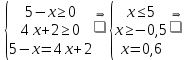 Ответ: 0,6 Пример 5. Решить уравнение: 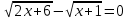 Решение. Запишем данное уравнение в виде: 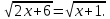 Возводя обе части в квадрат и учитывая, что Возводя обе части в квадрат и учитывая, что 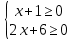 получим уравнение 2х+6=х+1, решение которого есть х = -5 – не удовлетворяет выписанному условию. Значит, данное уравнение не имеет решений. получим уравнение 2х+6=х+1, решение которого есть х = -5 – не удовлетворяет выписанному условию. Значит, данное уравнение не имеет решений.Ответ: нет решений Если иррациональное уравнение содержит несколько радикалов. В этом случае для избавления от радикалов уравнение приходится возводить в соответствующую степень несколько раз. При этом предварительно уединяют один из радикалов так, чтобы обе части уравнения стали неотрицательными. Особое внимание следует обратить на правильное нахождение ОДЗ. Пример 6. Решить уравнение Решение. Запишем уравнение в виде: Полученное уравнение равносильно исходному. Для его решения рассмотрим систему: 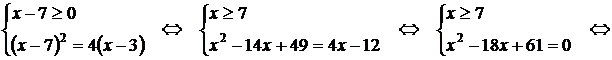 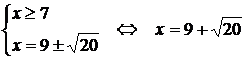 . .Ответ: Введение новой переменной в ряде случаев позволяет перейти от иррационального уравнения к рациональному уравнению. Пример 7. Решить уравнение Решение. Возведение данного уравнения в квадрат привело бы к уравнению четвертой степени, что нерационально. Поэтому запишем уравнение в виде Получим 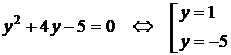 . .Вернемся к «старым» переменным 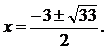 Ответ: Иногда при решении иррационального уравнения возникает необходимость ввести не одну, а несколько «новых» переменных. Такая ситуация возникает, например, при решении уравнений, содержащих радикалы разных степеней. Пример 8. Решить уравнение Решение. Пусть 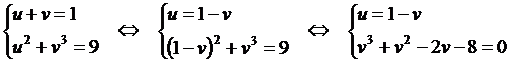 . .Решим последнее уравнение системы: 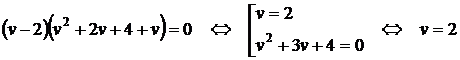 . .Получим, что Ответ: нет решений. При решении некоторых иррациональных уравнений нахождение области допустимых значений входящих в уравнение неизвестных может существенно облегчить решение уравнения. Пример 9. Решить уравнение 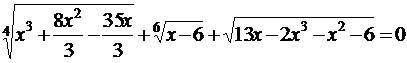 . .Решение. Данное уравнение имеет весьма громоздкий вид и неясно как подойти к его решению. Поэтому найдем сначала ОДЗ: 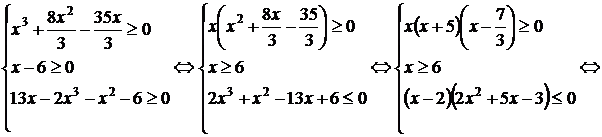 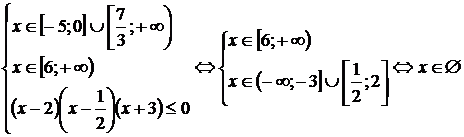 . .Получим, что область допустимых значений данного уравнения является пустым множеством и, следовательно, данное уравнение решений не имеет. Ответ: нет решений. При решении иррациональных уравнений бывает полезно воспользоваться монотонностью функций. Пример 10. Решить уравнение Решение. Один корень данного уравнения По свойству степенных функций функции Ответ: |
