ЭСб -19-2 47 Телешев Д.С. Задачи. Иркутский национальный исследовательский технический университет институт Энергетики Кафедра Электрических станций, сетей и систем
 Скачать 0.78 Mb. Скачать 0.78 Mb.
|
2.Постоянный ток в проводящей средеЗадача 2.1. Ток I, равный 16,16 А, течёт по проводнику длиной l, изготовленному из инвара, диаметр d сечения проводника равен 0,81 мм,. Определить сpeднюю скорость <υ>направленного движения электронов, считая, что концентрация n свободных электронов равна концентрации п' атомов проводника. Дано:
Средняя скорость направленного (упорядоченного) движения электронов определяется по формуле <υ>= 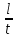 (1) (1)где t- время, в течение которого все свободные электроны, находящиеся в отрезке проводника между сечениями I и II, пройдя через сечение II (рис. 2.1), перенесут заряд Q=eN и создадут –ток 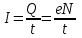 (2) (2)где е = 1,6*10-19К - элементарный заряд; N- число электронов в отрезке проводника. Число свободных электронов в отрезке проводника объёмом Vможно выразить следующим образом N=nV=nlS, (3) где S - площадь сечения. По условию задачи, п=п'. Следовательно, 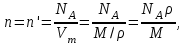 (4) (4)где NA = 6,02*1023 к моль-1 - постоянная Авогадро; Vm - молярный объём металла; М = 114,8 - молярная масса металла из таблицы 2.1; ρ - его плотность. Для инвара ρ = 8,7*103 кг/м3. Подставив последовательно выражения п из формулы (4) в равенство (3) и N из формулы (3) в равенство (2), получим 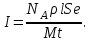 Отсюда найдём 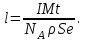 Подставив выражение lв формулу (1), сократив на t и выразив площадь S сечения проводника через диаметр d, найдём среднюю скорость направленного движения электронов: 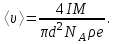 (5) (5)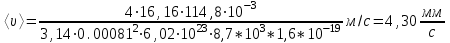 Ответ: 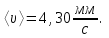 Задача 2.2. В цепь источника постоянного тока с ЭДС ε=7,28В включён резистор сопротивлением R=82,79Ом. Определить: 1) плотность тока в соединительных проводах площадью поперечного сечения S=2,19мм2; 2) число N электронов, проходящих через сечение проводов за время t= 1,54 с. Сопротивлением источника тока и соединительных проводов пренебречь. Дано:
1.Плотность тока по определению есть отношение силы тока I к площади поперечного сечения провода: j=I/S. (1) Силу тока в этой формуле выразим по закону Ома: 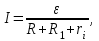 (2) (2)где R - сопротивление резистора; R1- сопротивление соединительных проводов; ri- внутреннее сопротивление источника тока. Пренебрегая сопротивлениями Rlи riиз (2), получим I =ε/R Подставив это выражение силы тока в (1), найдём j =ε/(RS). 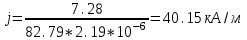 2. Число электронов, проходящих за время t через поперечное сечение, найдём, разделив заряд Q, протекающий за это время через сечение, на элементарный заряд N =Q/e, или с учётом того, что Q=It и I=ε/R, получим 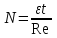 . .Подставим сюда числовые значения величин и вычислим (элементарный заряд: e=1,60*10-19 Кл): 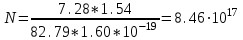 электронов электроновОтвет: 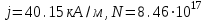 электронов. электронов.Задача 2.3 Пространство между пластинами плоского конденсатора имеет объём V=379 см3 и заполнено водородом, который частично ионизирован. Площадь пластин конденсатора S=251 см2. При каком напряжении U между пластинами конденсатора сила тока I, протекающего через конденсатор, достигнет значения 2, 63 мкА, если концентрация n ионов обоих знаков в газе равна 6,3*107 см-3. Принять подвижность ионов b+=5,4*10-4м2/(В*с), b–=7,4*10-4 м2/ (В*с). Дано:
Напряжение U на пластинах конденсатора связано с напряжённостью Е электрического поля между пластинами и расстоянием d между ними соотношением U=Ed. (1) Напряжённость поля может быть найдена из выражения плотности тока j=Qn(b++b-)E, где Q - заряд иона. Отсюда 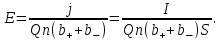 Расстояние dмежду пластинами, входящее в формулу (1), найдём из соотношения d=V/S. Подставив выражения Е и dв (1), получим 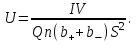 (2) (2)Проверим, дает ли правая часть полученной расчётной формулы единицу напряжения: 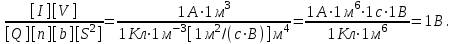 Подставим в формулу (2) значения величин и произведём вычисления: 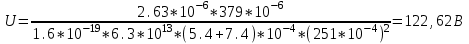 Ответ:U=122.62B |

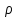 ,кг/м3
,кг/м3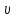 >,мм/с
>,мм/с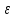 ,В
,В