ЭСб -19-2 47 Телешев Д.С. Задачи. Иркутский национальный исследовательский технический университет институт Энергетики Кафедра Электрических станций, сетей и систем
 Скачать 0.78 Mb. Скачать 0.78 Mb.
|
4. Силы, действующие на движущиеся заряды в магнитном поле.Задача 4.1. По двум параллельным прямым проводам длиной l=3,28 м каждый, находящимся на расстоянии d=23,2см друг от друга, текут одинаковые токи I=1,24 кА. Вычислить силу Fвзаимодействия токов. Дано:
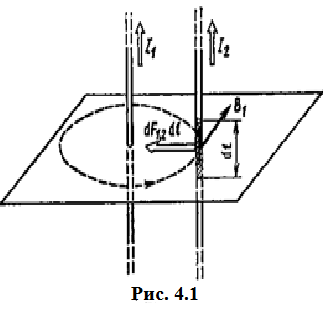 Вычислим силу F1,2, с которой магнитное поле, созданное током I1, действует на проводник с током I2. Для этого проведём магнитную силовую линию так (штриховая линия на рис. 4.1), чтобы она касалась проводника с током I2. По касательной к силовой линии проведём вектор магнитной индукции В1. Модуль магнитной индукции B1 определяется соотношением 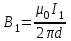 (1) (1)Согласно закону Ампера, на каждый элемент второго проводника с током I2 длиной dl2 действует в магнитном поле сила (длинный проводник (l>>d) можно приближенно рассматривать как бесконечно длинный) 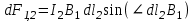 Так как отрезок dl перпендикулярен вектору B1, то 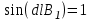 и тогда и тогдаСилу F1,2 взаимодействия (по третьему закону Ньютона, сила, действующая на первый проводник со стороны второго, будет равна найденной по модулю и противоположной по направлению) проводников с током найдём интегрированием по всей длине второго проводника; Заметив, что I1=I2=I и l2=l, получим 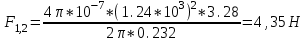   Ответ: Ответ: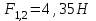 Задача 4.2 Провод в виде тонкого полукольца радиусом R=10,2 см находится в однородном магнитном поле (B=68 мТл). По проводу течёт ток I=15,5 А. Найти силу F, действующую на провод, если плоскость полукольца перпендикулярна линиям магнитной индукции, а подводящие провода находятся вне поля. 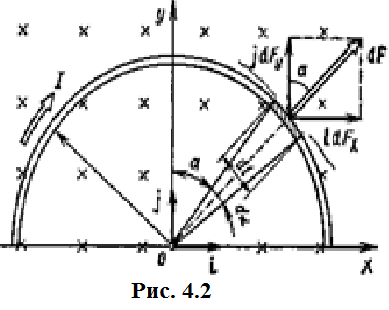 Дано:
Расположим провод в плоскости чертежа перпендикулярно линиям магнитной индукции (рис. 4.2) и выделим на нем малый элемент dl с током. На этот элемент тока Idlбудет действовать по закону Ампера сила dF=I[dlB]. Направление этой силы можно определить по правилу векторного произведения или по правилу левой руки. Используя симметрию, выберем координатные оси так, как это изображено на рис. 4.2. Силу dF представим в виде 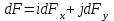 где i и j – единичные векторы (орты); dFxи dFy — проекции вектора dF на координатные оси Ох и Оу. Силу F, действующую на весь провод, найдём интегрированием: 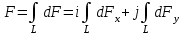 где символ Lуказывает на то, что интегрирование ведется по всей длине провода L. Из соображений симметрии первый интеграл равен нулю 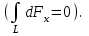 тогда тогда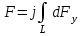 (1) (1)Из рис. 4.2 следует, что где dF – модуль вектора 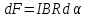 Тогда 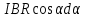 Введём dFyпод интеграл соотношения (1) и проинтегрируем в пределах от -π/2 до +π/2 (как это следует из рис. 4.2): Из полученного выражения видно, что сила F сонаправлена с положительным направлением оси Оу (единичным вектором j). Найдём модуль силы F: F=2*68*10-3*0.102*15.5=0.21 Н Ответ:F=0.21 Н Задача 4.3. На проволочный виток радиусом г=13,5см, помещенный между полюсами магнита, действует максимальный механический момент Мmax=7,5 мкН. Сила тока I в витке равна 3.5 А. Определить магнитную индукцию Вполя между полюсами магнита. Действием магнитного поля Земли пренебречь. Дано:
Индукцию Вмагнитного поля можно определить из выражения механического момента, действующего на виток с током в магнитном поле, Если учесть, что максимальное значение механический момент принимает при α=π/2(sin α=l), а также что pm=IS, то формула (1) примет вид Отсюда, учитывая, что S=πr2, находим Произведя вычисления по формуле (2), найдём 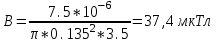 Ответ:В=37,4 мкТл |

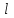 ,м
,м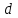 ,см
,см